Fragments' velocity of eccentric warheadwith double symmetric detonators
-
摘要: 在极坐标下基于弹塑性基本方程建立了壳体膨胀的运动方程,且考虑了两点对称偏心起爆的碰撞效应,利用Whitham方法对两对称爆轰波的碰撞叠加进行了计算,得到了三波点的迹线、马赫波超压及马赫杆的高度等参数。通过联合求解,导出了马赫波区破片的初速计算公式,并利用AUTODYN软件进行了数值模拟,理论计算与数值模拟结果符合较好,验证了理论模型的可靠性。计算结果表明,两点对称偏心起爆时定向区破片初速增益超过30%,起爆点的夹角变化对破片的初速大小及飞散偏转影响并不明显。Abstract: Eccentric warhead is a typical directional warhead, and its explosive wave is adjusted to improve the fragments' velocity in a specified area. The kinematic equation of a case was established in the polar coordinate system, and the Whitham method was adopted to realize the interaction of a double symmetric explosive wave, thus obtaining the trace of the triple wave point, the pressure and the height of the Mach stick, which were then calculated. By the combination of the kinematic equation and the Mach reflection, formula were deduced to evaluate the fragments' velocity in the Mach area. Comparison of the results obtained with AUTODYN 2D simulation shows that they are in good agreement. Double symmetric initiations increase the fragment's velocity by more than 30%, and the variation of the angle between initiations has little effect on the fragments' distribution and velocity.
-
Key words:
- mechanics of explosion /
- Mach effects /
- AUTODYN software /
- eccentric initiation /
- explosive wave
-
表 1 马赫波区计算结果
Table 1. Results in Mach domain
2φ/° xO2/mm yO2/mm h/mm v p 45 0 -50.1 32.5 1.34 1.30 60 0 -34.8 24.8 1.39 1.60 90 0 -2.70 14.1 1.50 1.90 表 2 破片初速的增益
Table 2. Increment of velocity in Mach domain
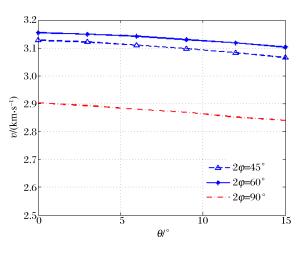
2φ/° vth/ δth/% vnum/ δnum/% ε/% (km·s-1) (km·s-1) 45 3.101 37.1 2.927 29.4 5.6 60 3.123 38.0 2.943 30.1 5.7 90 2.892 27.8 2.950 30.4 2.0 -
[1] 冯顺山, 蒋建伟, 何顺录, 等.偏轴心起爆破片初速径向分布规律研究[J].兵工学报, 1993(增刊):12-16. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000001078558Feng Shunshan, Jiang Jianwei, He Shunlu, et al. On the pattern of radial distribution pattern of initial velocities of fragments under asymmetrical initiation[J]. Acta Armament, 1993(suppl):12-16. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000001078558 [2] 王树山, 马晓飞, 隋树元, 等.偏心多点起爆战斗部破片飞散实验研究[J].北京理工大学学报, 2001, 21(2):177-179. doi: 10.3969/j.issn.1001-0645.2001.02.008Wang Shushan, Ma Xiaofei, Sui Shuyuan, et al. Experimental research on fagments dispersion of the warhead under asymmetrical multi-spots initiation[J]. Transactions of Beijing Institute of Technology, 2001, 21(2):177-179. doi: 10.3969/j.issn.1001-0645.2001.02.008 [3] 王晓英, 张庆明, 李金柱.偏心多点起爆战斗部破片飞散三维数值模拟研究[J].北京理工大学学报, 2003, 23(增刊):201-206. http://d.old.wanfangdata.com.cn/Conference/4506269Wang Xiaoying, Zhang Qingming, Li Jinzhu. 3D simulation of the fragments dispersion under asymmetrical multiple point initiation[J]. Transactions of Beijing Institute of Technology, 2003, 23(suppl):201-206. http://d.old.wanfangdata.com.cn/Conference/4506269 [4] 叶小军, 韩玉, 陈庆宝.偏心起爆战斗部速度增益的数值模拟及实验[J].火炸药学报, 2009, 32(3):29-34. doi: 10.3969/j.issn.1007-7812.2009.03.009Ye Xiaojun, Han Yu, Chen Qingbao. Numerical simulation and experiment of velocity gains on the non-central detonation warhead[J]. Chinese Journal of Explosives & Propellants, 2009, 32(3):29-34. doi: 10.3969/j.issn.1007-7812.2009.03.009 [5] 陈放, 马晓青, 段祝平.偏心起爆定向战斗部破片初速分布规律研究[C]//中国力学学会学术大会.北京, 2005. [6] 王马法, 卢芳云, 李翔宇.爆轰波斜冲击作用下破片飞散特性研究[J].国防科技大学学报, 2013, 35(1):60-64. doi: 10.3969/j.issn.1001-2486.2013.01.012Wang Mafa, Lu Fangyun, Li Xiangyu, et al. Research on the projection characteristics of fragments under the loading of the oblique shock wave[J]. Journal of National University of Defense Technology, 2013, 35(1):60-64. doi: 10.3969/j.issn.1001-2486.2013.01.012 [7] 王继海.二维非定常流和激波[M].北京:科学出版社, 1994. [8] 北京工业学院八系.爆炸及其作用(上册)[M].北京, 1978. [9] 武伟明, 佟浩然.定向杀伤战斗部结构与破片增益的关系[J].兵工学报:弹箭分册, 1992(1):81-85 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000000227104 -






 下载:
下载: