Mechanical model of the grooved-tapered projectile penetrating concrete targets
-
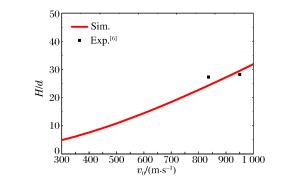
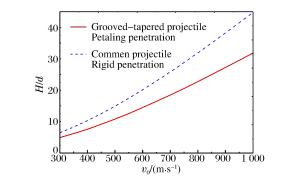
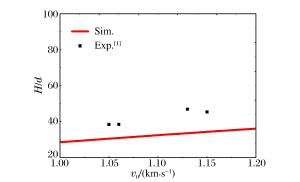
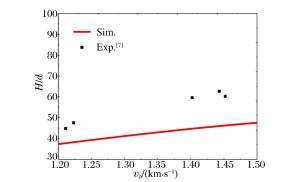
摘要: 利用混凝土材料的动态球形空腔膨胀理论,建立了针对刻槽弹体的低速花瓣形受力模型和高速圆孔形受力模型,并采用这两种模型计算了刻槽弹体侵彻混凝土的侵深。结果表明:当初速低于1 000 m/s时,运用低速花瓣形受力模型计算得出的侵深和实验值的误差小于11%;当初速高于1 000 m/s时,运用高速圆孔形受力模型计算出的侵深和实验值的误差约为20%。综合实验过程和实验误差分析可知,建立的刻槽弹侵彻混凝土受力模型可用于刻槽弹对混凝土的侵彻能力分析。Abstract: Based on the theory of dynamic spherical cavity expansion, the model of the petaling penetration at low speed and the round hole penetration at high speed were established to describe the penetration by the grooved-tapered projectile and the penetration depths were calculated using the models. Our results indicate that the error of the penetration depth between the theoretical calculation and the experimental data is less than 11% when the initial velocity is below 1000 m/s, and this error reaches about 20% when the initial velocity is above 1 000 m/s. Comsidering the experimental error caused by the separated targets, we believe that the models can be used to predict the penetration depth for the grooved-tapered projectile penetrating concrete targets.
-
表 1 刻槽弹体侵彻混凝土计算误差(v0 < 1 200 m/s)
Table 1. Calculation error of the projectile penetrating the concrete (v0 < 1 200 m/s)
v0/(m·s-1) δ/% 圆孔模型 花瓣模型 1 054 20.2 22.9 1 060 19.6 22.4 1 130 28.4 30.7 1 150 24.4 26.8 表 2 刻槽弹体侵彻混凝土计算误差(v0>1 200 m/s)
Table 2. Table 2Calculation error of the projectile penetrating the concrete (v0>1 200 m/s)
v0/(m·s-1) δ/% 圆孔模型 花瓣模型 1211 15.7 18.5 1443 26.6 28.6 1223 19.5 22.2 1 402 25.0 27.1 1 452 23.2 25.2 -
[1] 梁斌, 陈小伟, 姬永强, 等.先进钻地弹概念弹的次口径高速深侵彻实验研究[J].爆炸与冲击, 2008, 28(1):1-9. doi: 10.3321/j.issn:1001-1455.2008.01.001Liang Bin, Chen Xiaowei, Ji Yongqiang, et al. Experimental study on deep penetration of reduced-scale advanced earth penetrating weapon[J]. Explosion and Shock Waves, 2008, 28(1):1-9. doi: 10.3321/j.issn:1001-1455.2008.01.001 [2] 王一楠.动能弹体高速侵彻混凝土机理研究[D].北京: 北京理工大学, 2009. [3] Wu H J, Qian F, Huang F L, et al. Projectile nose mass abrasion of high-speed penetration into concrete[J]. Advances in Mechanical Engineering, 2012, 4(6):512-530. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_97da7bc3256c93bf024a9ccbfbfefc90 [4] Wu H J, Huang F L, Wang Y N, et al. Mass loss and nose shape change on ogive-nose steel projectiles during concrete penetration[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2012, 13(3):273-280. http://cn.bing.com/academic/profile?id=c4a6ed7406e7152265f47e892e0c9cba&encoded=0&v=paper_preview&mkt=zh-cn [5] Wu H J, Wang Y N, Shan Y, et al. Mechanism of high-velocity projectile penetration into concrete[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2012, 13(2):137-143. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0226220937/ [6] Wu H J, Wang Y N, Huang F L. Penetration concrete targets experiments with non-ideal & high velocity between 800 and 1 100 m/s[J]. International Journal of Modern Physics B, 2012, 22(9/10/11):1087-1093. doi: 10.1142/S0217979208046360 [7] Erengil M E, Cargile D J. Advanced projectile concept for high speed penetration of concrete targets[C]//Proceedings of the 20th International Symposium on Ballistics. Orlando, Florida, 2002: 23-27. -







 下载:
下载: