Numerical investigation of shield building for nuclear power plant subjected to commercial aircraft impact
-
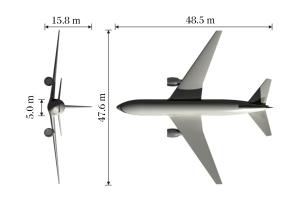
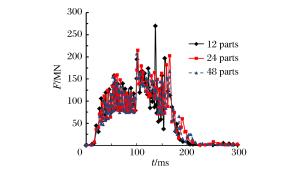
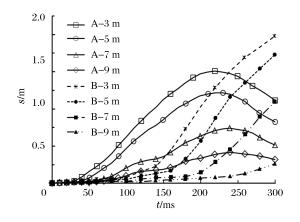
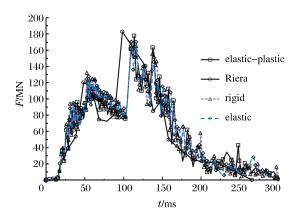
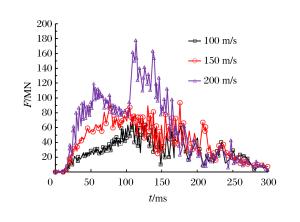
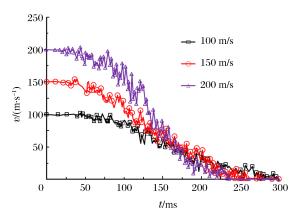
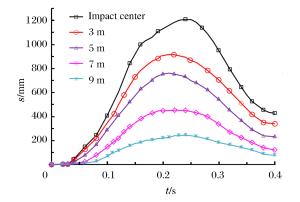
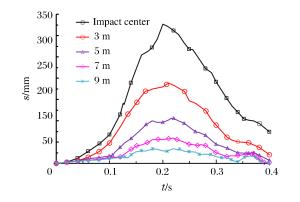
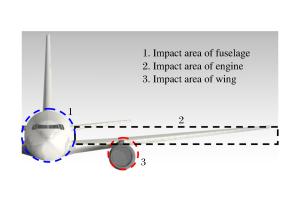
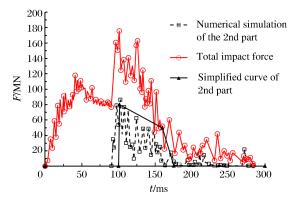
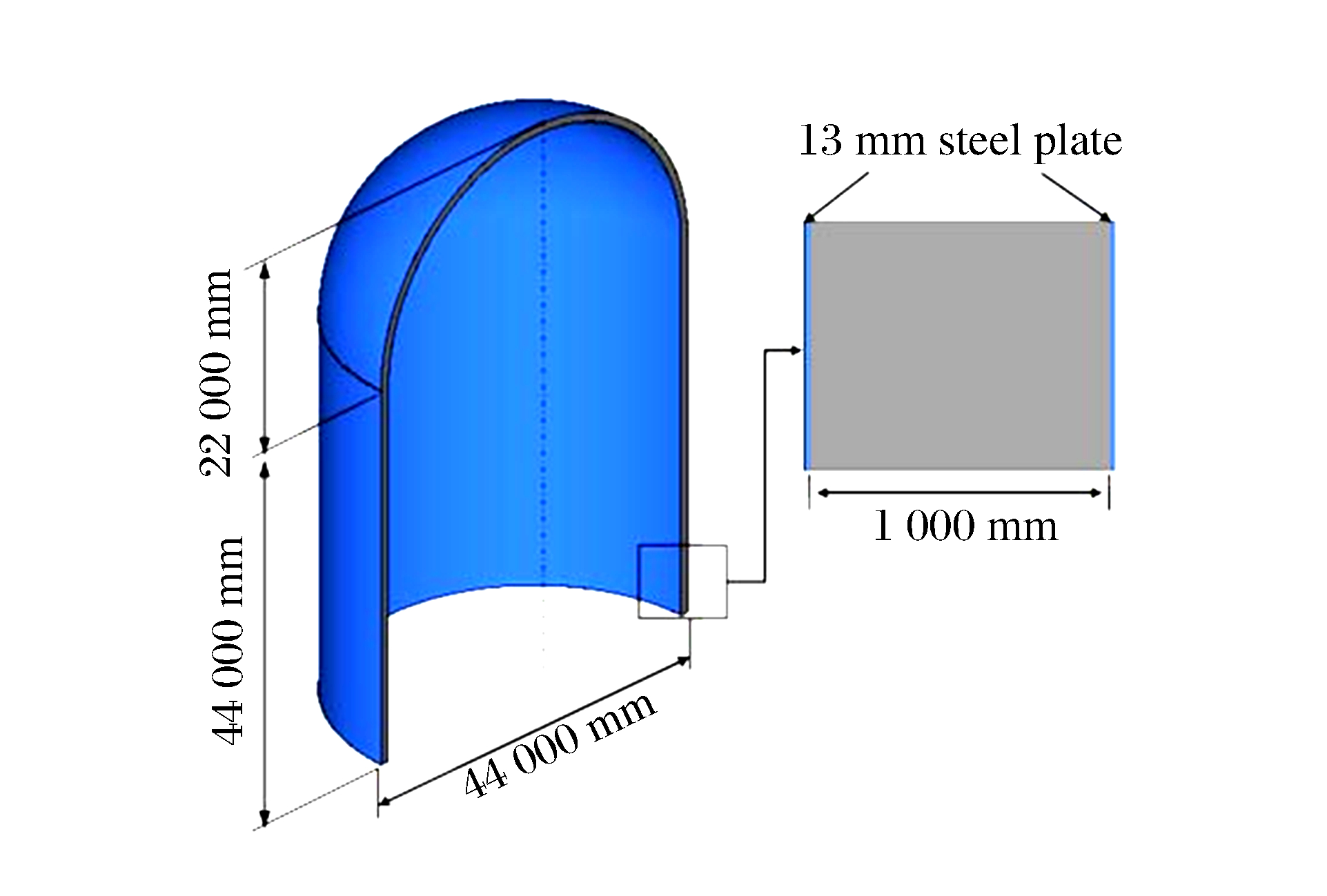
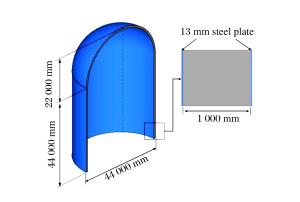
摘要: 为研究大型商用飞机撞击核电站屏蔽厂房的毁伤特性,建立了Boeing 767商用飞机和双钢板混凝土屏蔽厂房的有限元模型,模拟两者的相互撞击作用过程,得到飞机不同部位(机身、发动机)对屏蔽厂房的撞击力时程曲线,对每一个作用部分给出简化撞击力曲线和作用面积,确定了撞击力分布形式。结果分析表明:飞机轴向网格尺寸对撞击力影响较大;屏蔽厂房被撞击部位变形明显,其他区域变形较小;撞击速度对撞击作用时间影响较小,而对结构响应位移影响很大,撞击力合力随着撞击速度的降低迅速下降。Abstract: To study damage characteristics of the shield building for nuclear power plant subjected to a large commercial aircraft impact, finite element models for Boeing 767 commercial aircraft impacting on a shield building made of steel-concrete-steel sandwich panels are established to simulate the impact process. The following results were achieved: the aircraft's axial mesh size greatly influences the impact force; some parts of the shield building hit by the aircraft undergo significant deformations while the deformation is smaller in the other parts; the impact velocity has little effect on the impact duration but a great effect on the structural response displacement, and the total impact force rapidly declines with the impact velocity decreasing. The impact force arising from different parts of the aircraft hitting the shield building are given, the simplified curve and the load area of different impact forces are obtained, which will contribute to the determination of the impact force distribution form, thus providing a positive help to the engineering design of shield buildings.
-
Key words:
- solid mechanics /
- aircraft impact /
- shield building /
- finite element simulation /
- impact force /
- distribution form
-
表 1 计算参数
Table 1. Calculation parameters
材料 σy/MPa σs/MPa ρ/(kg·m-3) E/GPa T/GPa ν C P εpe 钢 447 - 7850 210 5 0.3 5 40 0.8 铝合金 503 - 2810 71.9 0.5 0.33 4 6500 0.1 混凝土 - 48 2300 - - 0.2 - - 0.17 -
[1] Riera J D. A critical reappraisal of nuclear power plant safety against accidental aircraft impact[J]. Nuclear Engineering and Design, 1980, 57(1):193-206. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/016224398100600403 [2] Henkel F O, Wölfel H. Building concept against airplane crash[J]. Nuclear Engineering and Design, 1984, 79(3):397-409. doi: 10.1016/0029-5493(84)90052-9 [3] 汤搏.关于核电厂防大型商用飞机撞击的要求-核电发展面临的新挑战[J].核安全, 2010(3):1-12. doi: 10.3969/j.issn.1672-5360.2010.03.001Tang Bo. Discussion on the impact of large commercial airplane to nuclear power plant[J]. Nuclear Safety, 2010(3):1-12. doi: 10.3969/j.issn.1672-5360.2010.03.001 [4] Luther W, Müller W C. FDS simulation of the fuel fireball from a hypothetical commercial airliner crash on a generic nuclear power plant[J]. Nuclear Engineering and Design, 2009, 239(10):2056-2069. doi: 10.1016/j.nucengdes.2009.04.018 [5] Riera J D. On the stress analysis of structures subjected to aircraft impact forces[J]. Nuclear Engineering and Design, 1968, 8(4):415-426. doi: 10.1016/0029-5493(68)90039-3 [6] Hornyik K. Analytic modeling of the impact of soft missiles on protective walls[C]//Proceedings of the 4th International Conference on Structural Mechanics in Reactor Technology. San Francisco, USA, 1977: 1-12. [7] Bahar L Y, Rice J S. Simplified derivation of the reaction-time history in aircraft impact on a nuclear power plant[J]. Nuclear Engineering and Design, 1978, 49(3):263-268. doi: 10.1016/0029-5493(78)90150-4 [8] Sugano T, Tsubota H, Kasai Y, et al. Full-scale aircraft impact test for evaluation of impact force[J]. Nuclear Engineering and Design, 1993, 140(3):373-385. doi: 10.1016/0029-5493(93)90119-T [9] Bangash M Y H. Shock, impact and explosion structural analysis and design[M]. Berlin: Springer Press, 2009. [10] Nachtsheim W, Stangenberg F. Selected results of Meppen slab tests-state of interpretation, comparison with computational investigations[C]//Proceedings of the 7th International Conference on Structural Mechanics in Reactor Technology. Chicago, USA, 1983: 379-386. [11] Rüdiger E, Riech H. Experimental and theoretical investigations on the impact of deformable missiles onto reinforced concrete slabs[C]//Proceedings of the 7th International Conference on Structural Mechanics in Reactor Technology. Chicago, USA, 1983: 387-394. [12] Herrmann N, Kreuser K, Stempniewski L. An experimental approach to determine load-functions for the impact of fluid-filled projectiles[C]//Proceedings of the 76th Shock and Vibration Symposium. Destin, Florida, USA, 2005. [13] Lastunen A, Hakola I, Järvinen E, et al. Impact test facility[C]//Proceedings of the 19th International Conference on Structural Mechanics in Reactor Technology. Toronto, Canada, 2007: 1-8. [14] Mizuno J, Koshika N, Morikawa H, et al. Investigation on impact resistance of steel plate reinforced concrete barriers against aircraft impact part1: test program and results[C]//Proceedings of the 18th International Conference on Structural Mechanics in Reactor Technology. Beijing, 2005: 2566-2579. [15] Riedel W, Nöldgena M, Straβburger E, et al. Local damage to ultra high performance concrete structures caused by an impact of aircraft engine missiles[J]. Nuclear Engineering and Design, 2010, 240(10):2633-2642. doi: 10.1016/j.nucengdes.2010.07.036 [16] Sugano T, Tsubota H, Kasai Y, et al. Local damage to reinforced concrete structures caused by impact of aircraft engine missiles Part 1: Test program, method and results[J]. Nuclear Engineering and Design, 1993, 140 (3):387-405. doi: 10.1016/0029-5493(93)90120-X [17] Sugano T, Tsubota H, Kasai Y, et al. Local damage to reinforced concrete structures caused by impact of aircraft engine missiles Part 2: Evaluation of test results[J]. Nuclear Engineering and Design, 1993, 140(3):407-423. doi: 10.1016/0029-5493(93)90121-O [18] Martina O, Centrob V, Schwoertzigb T. Finite element analysis on the Meppen-Ⅱ-4 Slab Test[J]. Nuclear Engineering and Design, 2012, 247:1-10. doi: 10.1016/j.nucengdes.2012.02.001 [19] Martina O, Centrob V, Schwoertzigb T. Finite element analysis on the VTT-IRSN flexural failure test[J]. Nuclear Engineering and Design, 2012, 252:1-10. doi: 10.1016/j.nucengdes.2012.07.004 [20] Iqbal M A, Rai S, Sadique M R, et al. Numerical simulation of aircraft crash on nuclear containment structure[J]. Nuclear Engineering and Design, 2012, 243:321-335. doi: 10.1016/j.nucengdes.2011.11.019 [21] Sadique M R, Iqbal M A, Bhargava P. Nuclear containment structure subjected to commercial and fighter aircraft crash[J]. Nuclear Engineering and Design, 2013, 260:30-46. doi: 10.1016/j.nucengdes.2013.03.009 [22] Lee K, Han S E, Hong J W. Analysis of impact of large commercial aircraft on a prestressed containment building[J]. Nuclear Engineering and Design, 2013, 265:431-449. doi: 10.1016/j.nucengdes.2013.09.009 [23] Jones N. Structural Impact[M]. UK: Cambridge University Press, 1989:385-400. [24] 王天运, 任辉启, 张力军, 等.常规装药侵彻预应力钢筋混凝土安全壳数值模拟[J].工程力学, 2005, 22(5):126-130. doi: 10.3969/j.issn.1000-4750.2005.05.023Wang Tianyun, Ren Huiqi, Zhang Lijun, et al. Numerical simulation of general bomb penetration into pre-stress reinforced concrete containment[J]. Engineering Mechanics, 2005, 22(5):126-130. doi: 10.3969/j.issn.1000-4750.2005.05.023 [25] 王雷, 李玉龙, 索涛, 等.航空常用铝合金动态拉伸力学性能探究[J].航空材料学报, 2013, 33(4):71-77. http://d.old.wanfangdata.com.cn/Periodical/hkclxb201304013Wang Lei, Li Yulong, Suo Tao, et al. Mechanical behavior of commonly used aeronautical aluminum alloys under dynamic tension[J]. Journal of Aeronautical Materials, 2013, 33(4):71-77. http://d.old.wanfangdata.com.cn/Periodical/hkclxb201304013 [26] Malvar L J, Ross C A. Review of strain rate effects for concrete in tension[J]. ACI Materials Journal, 1998, 96(5):735-739. http://cn.bing.com/academic/profile?id=97209aeec680a4179187bf18b762a71e&encoded=0&v=paper_preview&mkt=zh-cn [27] Prabhakar G, Ranjan R, Mini K P, et al. Analysis of aircraft impact on containment structure[C]//Proceedings of the 5th Asia-Pacific Conference on Shock & Impact Loads on Structures. Changsha, China, 2003: 315-322. [28] 刘晶波, 郑文凯.大型商用飞机撞击核电站屏蔽厂房荷载研究[J].振动与冲击, 2014, 33(6):97-112. http://d.old.wanfangdata.com.cn/Periodical/zdycj201406018Liu Jingbo, Zheng Wenkai. Impact load analysis on a nuclear power plant impacted by a large commercial aircraft[J]. Journal of Vibration and Shock, 2014, 33(6):97-112. http://d.old.wanfangdata.com.cn/Periodical/zdycj201406018 [29] 中华人民共和国住房和城乡建设部.混凝土结构设计规范GB 50010-2010[S].北京: 中华人民共和国住房和城乡建设部, 2010. -






 下载:
下载: