Application of multiple-population genetic algorithm in parameter identification for PBX constitutive model
-
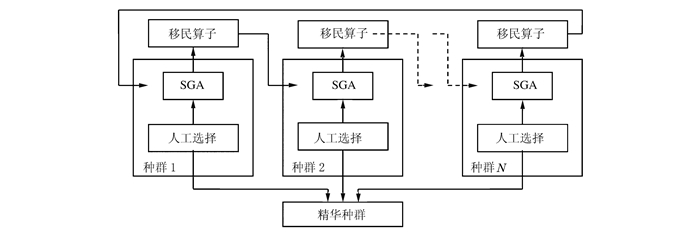
摘要: 利用多种群并行结构对标准遗传算法SGA进行并行化处理,引入移民算子和精华种群形成多种群遗传算法MPGA,并设计了自适应交叉和变异概率对算法的收敛速度进行改进。结合ABAQUS软件和改进的多种群遗传算法,建立了材料本构模型参数识别方法。采用该方法对PBX炸药黏弹性损伤本构模型参数进行了模拟识别,并同基于标准遗传算法的参数识别方法进行了比较。结果证明,基于改进多种群遗传算法IMPGA的方法对克服算法未成熟收敛有显著的效果,识别结果更稳定。同时该方法的收敛速度更快,寻优能力更强,适合复杂非线性问题的优化,此方法可以被应用到其他材料本构模型的参数识别中。Abstract: In this work, the standard genetic algorithm (SGA) was parallel processed using multiple parallel structures. Based on the structures, a multiple-population genetic algorithm (MPGA) was established by introducing the immigration operator and quintessence population. Self-adaptive operators of crossover probability and mutation probability were designed to improve the convergence speed of the MPGA. Combining ABAQUS with the improved multiple-population genetic optimized algorithm, a parameter identification method of constitutive model was built. Using the proposed method, a simulation example of parameter identification for PBX viscoelastic damage constitutive model was carried out. Comparison was made between methods based on SGA and MPGA. The results show that the MPGA method can effectively overcome the difficulty of the premature convergence and the identification result is more robust. The method is suitable for the optimization of complex nonlinear systems due to its superiority in the convergence speed and searching ability, and it can be applied to the parameter identification of other models.
-
表 1 参数识别结果
Table 1. Results of parameter identification
识别参数 真实值 取值范围 SGA识别 MPGA识别 IMPGA识别 结果 误差/% 结果 误差/% 结果 误差/% E/MPa 496.1 400~600 507.142 2.22 504.931 1.78 505.306 1.86 ν 0.38 0.2~0.6 0.372 2.17 0.387 1.93 0.373 1.84 η 260 200~300 252.460 2.90 263.38 1.30 263.256 1.25 βm 0.6 0.3~0.9 0.619 3.17 0.613 2.09 0.587 2.16 βs 0.4 0.1~0.7 0.384 3.86 0.414 3.40 0.413 3.25 χ 155.5 100~200 148.814 4.30 149.358 3.95 149.249 4.02 n 0.628 0.3~0.9 0.643 2.38 0.638 1.73 0.639 1.75 -
[1] 梁增友.炸药冲击损伤与起爆特性[M].北京:电子工业出版社, 2009. [2] 郭虎, 罗景润.循环载荷下PBX力学行为研究[J].爆炸与冲击, 2013, 33(增刊1): 105-110. http://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ2013S1019.htmGuo Hu, Luo Jingrun. Mechanical behavior of PBX under cyclic loadings[J]. Explosion and Shock Waves, 2013, 33(Suppl 1):105-110. http://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ2013S1019.htm [3] Rauchs G, Bardon J. Identification of elasto-viscoplastic material parameters by indentation testing and combined finite element modelling and numerical optimization[J]. Finite Elements in Analysis and Design, 2011, 47(7):653-667. doi: 10.1016/j.finel.2011.01.008 [4] Springmann M, Kuna M. Identification of material parameters of the Gurson-Tvergaard-Needleman model by combined experimental and numerical techniques[J]. Computational Materials Science, 2005, 32(3/4):544-552. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f907b29be395d8906bcc03bac71e5e48 [5] Chaparro B M, Thuillier S, Menezes L F, et al. Material parameters identification: Gradient-based, genetic and hybrid optimization algorithms[J]. Computational Materials Science, 2008, 44(2):339-346. doi: 10.1016/j.commatsci.2008.03.028 [6] Majzoobi G H, Dehgolan F R. Determination of the constants of damage models[J]. Procedia Engineering, 2011, 10:764-773. doi: 10.1016/j.proeng.2011.04.127 [7] Muñoz-Rojas P A, Cardoso E L, Vaz M. Parameter identification of damage models using genetic algorithms[J]. Experimental Mechanics, 2010, 50(5):627-634. doi: 10.1007/s11340-009-9321-y [8] 陈炳瑞, 冯夏庭, 丁秀丽, 等.基于模式-遗传-神经网络的流变参数反演[J].岩石力学与工程学报, 2005, 24(4): 553-558. doi: 10.3321/j.issn:1000-6915.2005.04.002Chen Bingrui, Feng Xiating, Ding Xiuli, et al. Back analysis on rheological parameters based on pattern-genetic-neural network[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4):553-558. doi: 10.3321/j.issn:1000-6915.2005.04.002 [9] 高军, 黄再兴. PBX炸药粘弹性损伤本构模型的参数识别[J].工程力学, 2013, 30(7): 299-304. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201307045Gao Jun, Huang Zaixing. Parameter identification for viscoelastic damage constitutive model of PBX[J]. Engineering Mechanics, 2013, 30(7): 299-304. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201307045 [10] Solano G J, Rodriguez V K, Garcia N D. Model-based spectral estimation of Doppler signals using parallel genetic algorithms[J]. Artificial Intelligence in Medicine, 2000, 19(1):75-89. doi: 10.1016/S0933-3657(99)00051-2 [11] 李守巨, 刘迎曦, 孙伟.智能计算与参数反演[M].北京:科学出版社, 2008. [12] Cantu-Paz E. Designing efficient and accurate parallel genetic algorithms (parallel algorithms)[D]. University of Illinois at Urbana-Champaign, 1999. http://link.springer.com/978-1-4615-4369-5 [13] Potts J C, Giddens T D, Yadav S B. The development and evaluation of an improved genetic algorithm based on migration and artificial selection[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1994, 24(1):73-86. doi: 10.1109/21.259687 [14] 刘桂萍.基于微型遗传算法的多目标优化方法及应用研究[D].长沙: 湖南大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10532-2008081553.htm [15] Sheblé G B, Brittig K. Refined genetic algorithm-economic dispatch example[J]. IEEE Transactions on Power Systems, 1995, 10(1):117-124. doi: 10.1109/59.373934 [16] Paris P C, Erdogan F. A critical analysis of crack propagation laws[J]. Journal of Fluids Engineering, 1963, 85(4):528-533. -






 下载:
下载: