Dynamic buckling analysis of functionally graded beam under thermal shock in Hamilton system
-
摘要: 在Hamilton体系下，基于Euler梁理论研究了功能梯度材料梁受热冲击载荷作用时的动力屈曲问题；将非均匀功能梯度复合材料的物性参数假设为厚度坐标的幂函数形式，采用Laplace变换法和幂级数法解析求得热冲击下功能梯度梁内的动态温度场：首先将功能梯度梁的屈曲问题归结为辛空间中系统的零本征值问题，梁的屈曲载荷与屈曲模态分别对应于Hamilton体系下的辛本征值和本征解问题，由分叉条件求得屈曲模态和屈曲热轴力，根据屈曲热轴力求解临界屈曲升温载荷。给出了热冲击载荷作用下一类非均匀梯度材料梁屈曲特性的辛方法研究过程，讨论了材料的梯度特性、结构几何参数和热冲击载荷参数对临界温度的影响。Abstract: Based on the Euler beam theory, the dynamic buckling of the functionally graded beam subjected to thermal shock was investigated in the Hamilton system. The material properties of the functionally graded beam were assumed to be graded in the thickness direction according to a simple power law distribution in terms of the volume fractions of the constituents. The transient temperature fields were solved analytically using the Laplace transform and power series method. It was shown that the dynamic buckling problem can be reduced to a zero-eigenvalue problem in the symplectic space, the buckling loading and the buckling mode of the FGM beam correspond to the generalized eigenvalue and eigen solution. The buckling mode and the buckling thermal axial forces can be obtained through bifurcation condition, and the buckling temperature rise of the FGM beam can be obtained by inverse solution. In this research, the solution process for dynamic buckling of the FGM beam subjected to thermal shock using the symplectic method were given, and the effects of the material constitution, geometric parameters and the parameters of thermal shock load on the critical temperature were discussed.
-
Key words:
- functionally graded materials /
- Euler beam /
- thermal shock /
- symplectic method /
- dynamic buckling
-
图 5 FGM梁的1、2阶屈曲升温随k的变化
Figure 5. Variations of first and second order buckling temperature rise with k
图 6 不同a时FGM梁的临界屈曲升温(ΔT)l
Figure 6. Variations of critical temperature for specified values of a
表 1 陶瓷梁的静态热屈曲量纲一临界温度
Table 1. The static non-dimensional critical buckling temperature of ceramic beam
下载: 导出CSV
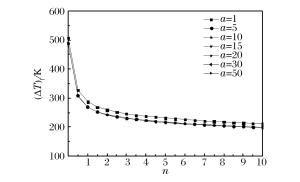
表 2 功能梯度梁的各阶屈曲升温
Table 2. Buckling temperature rise of FGM beam
n θn ΔT/K SiC k=0.5 k=1 k=2 k=5 k=10 k=100 Ni 1 39.47 488.26 307.64 268.63 242.02 216.39 198.53 167.88 163.46 2 80.76 999.04 629.48 549.65 495.21 442.76 406.21 343.50 334.46 3 157.91 1953.43 1230.82 1074.73 968.29 865.73 794.27 671.66 653.97
下载: 导出CSV
表 3 不同换热系数(hr)时FGM梁的临界屈曲升温
Table 3. Critical temperature rise of FGM beam for some specified values of hr
hr ΔT/K SiC k=0.5 k=1 k=2 k=5 k=10 k=100 Ni 10 487.31 306.98 268.09 241.57 216.01 198.19 167.6 163.18 30 487.79 307.31 268.36 241.8 216.2 198.36 167.74 163.32 50 488.26 307.64 268.63 242.02 216.39 198.53 167.88 163.46 70 488.73 307.97 268.9 242.25 216.58 198.69 168.02 163.59
下载: 导出CSV
表 4 不同长细比(λ)下FGM梁的临界屈曲升温(ΔT)l
Table 4. Critical temperature rise of FGM beam for some specified values of λ
λ (ΔT)l/K SiC k=0.5 k=1 k=2 k=5 k=10 k=100 Ni 30 868.02 546.92 477.57 430.27 384.69 352.94 298.45 290.59 40 488.26 307.64 268.63 242.02 216.39 198.53 167.88 163.46 50 312.49 196.89 171.92 154.89 138.49 127.05 107.44 104.61 60 258.25 162.72 142.08 128.01 114.45 105.00 88.79 86.45
下载: 导出CSV
表 5 热冲击载荷作用时间(Δt)不同时FGM梁的临界屈曲升温(ΔT)l
Table 5. Critical temperature rise of FGM beam for some specified values of Δt
Δt/s (ΔT)l/K SiC k=0.5 k=1 k=2 k=5 k=10 k=100 Ni 1 805.26 600.65 534.75 481.04 421.57 378.73 310.23 302.12 2 589.07 415.66 368.42 331.62 292.37 264.47 219.63 213.83 5 488.26 307.64 268.63 242.02 216.39 198.53 167.88 163.46 10 479.57 289.57 250.81 225.92 203.5 187.99 160.13 155.91 ∞ 479.39 288.26 249.28 224.58 202.55 187.3 159.69 155.48
下载: 导出CSV
-
[1] 仲政, 吴林志, 陈伟球.功能梯度材料与结构的若干力学问题研究进展[J].力学进展, 2010, 40(5):528-541. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201002077615Zhong Zheng, Wu Linzhi, Chen Weiqiu.Pregress in the study on mechanics problems of functionally graded materials and structures[J].Advances in Mechanics, 2010, 40(5):528-541. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201002077615 [2] 张靖华, 潘双超, 李世荣.热冲击下功能梯度圆板的动力屈曲[J].应用力学学报, 2015, 32(6):901-907. http://d.old.wanfangdata.com.cn/Periodical/yylxxb201506003Zhang Jinghua, Pan Shuangchao, Li Shirong.Dynamic buckling of functionally graded circular plate under thermal shock[J].Chinese Journal of Applied Mechanics, 2015, 32(6):901-907. http://d.old.wanfangdata.com.cn/Periodical/yylxxb201506003 [3] Mehrian S M N, Naei M H.Two dimensional analysis of functionally graded partial annular disk under radial thermal shock using hybrid Fourier-Laplace transform[J].Applied Mechanics and Materials, 2013, 436:92-99. doi: 10.4028/www.scientific.net/AMM.436 [4] Mirzavand B, Eslami M R, Shakeri M.Dynamic thermal postbuckling analysis of piezoelectric functionally graded cylindrical shells[J].Journal of Thermal Stresses, 2010, 33(7):646-660. doi: 10.1080/01495731003776010 [5] Mirzavand B, Eslami M R, Reddy J N.Dynamic thermal postbuckling analysis of shear deformable piezoelectric FGM cylindrical shells[J].Journal of Thermal Stresses, 2013, 36(3):189-206. doi: 10.1080/01495739.2013.768443 [6] Ma L S, Wang T J.Relationships between the solutions of axisymmetric bending and buckling of functionally graded circular plates based on the third-order plate theory and the classical solutions for isotropic circular plates[J].International Journal of Solids and Structures, 2004, 41(1):85-101. doi: 10.1016/j.ijsolstr.2003.09.008 [7] Li S R, Zhang J H, Zhao Y G.Thermal post-buckling of functionally graded material Timoshenko beams[J].Applied Mathematics and Mechanics, 2006, 27(6):803-811. doi: 10.1007/s10483-006-0611-y [8] Li S R, Zhang J H, Zhao Y G.Nonlinear thermo-mechanical post-buckling of circular FGM plate with geometric imperfection[J].Thin Walled Structures, 2007, 45(5):528-536. doi: 10.1016/j.tws.2007.04.002 [9] Shegokar N L, Lal A.Thermo-electromechanically induced stochastic post buckling response of piezoelectric functionally graded beam[J].International Journal of Mechanics and Materials in Design, 2014, 10(3):329-349. doi: 10.1007/s10999-014-9246-1 [10] Shariyat M.Dynamic thermal buckling of suddenly heated temperature-dependent FGM cylindrical shells under combined axial compression and external pressure[J].International Journal of Solids and Structures, 2008, 45(9):2598-2612. doi: 10.1016/j.ijsolstr.2007.12.015 [11] Sohn K J, Kim J H.Structural stability of functionally graded panels subjected to aero-thermal loads[J].Composite Structure, 2007, 82(3):317-325. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=11f85b2888164944f65097acd729e1bc [12] 徐新生, 段政, 马源, 等.辛方法和弹性圆柱壳在内外压和轴向冲击下的动态屈曲[J].爆炸与冲击, 2007, 27(6):509-514. doi: 10.3321/j.issn:1001-1455.2007.06.005Xu Xinsheng, Duan Zheng, Ma Yuan, et al.A symplectic method and dynamic buckling of elastic cylindrical shells under both axial impact and internal or external pressure[J].Explosion and Shock Waves, 2007, 27(6):509-514. doi: 10.3321/j.issn:1001-1455.2007.06.005 [13] 谈梅兰, 吴光, 王鑫伟.矩形薄板面内非线性分布载荷下的辛弹性力学解[J].工程力学, 2008, 25(10):50-53. http://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200810012.htmTan Meilan, Wu Guang, Wang Xinwei.Symplectic elasticity solutions for thin rectangular plates subjected to nonlinear distributed in plane loadings[J].Engineering Mechanics, 2008, 25(10):50-53. http://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200810012.htm [14] 刘淼.功能梯度材料结构的非传统Hamilton变分原理及其有限元法[D].上海: 同济大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10247-2008049158.htm [15] 褚洪杰, 徐新生, 林志华, 等.弹性梁非线性热屈曲行为与辛本征解展开方法[J].大连理工大学学报, 2011, 51(1):1-6. doi: 10.3969/j.issn.1008-407X.2011.01.001Chu Hongjie, Xu Xinsheng, Ling Zhihua, et al.Nonlinear thermal buckling of elastic beams and expanding method of symplectic eigensolutions[J].Journal of Dalian University of Technology, 2011, 51(1):1-6. doi: 10.3969/j.issn.1008-407X.2011.01.001 [16] Sun J B, Xu X S, Lim C W.Buckling of functionally graded cylindrical shells under combined thermal and compressive loads[J].Journal of Thermal Stresses, 2014, 37(3):340-362. doi: 10.1080/01495739.2013.869143 [17] Zhang J H, Li G Z, Li S R.DQM based thermal stresses analysis of a FG cylindrical shell under thermal shock[J].Journal of Thermal Stresses, 2015, 38(9), 959-982. doi: 10.1080/01495739.2015.1038488 -
点击查看大图
图(6) / 表(5)
计量
- 文章访问数: 4388
- HTML全文浏览量: 1332
- PDF下载量: 403
- 被引次数: 0