液滴对爆炸冲击波的衰减作用

刘贵兵; 侯海量; 朱锡; 张国栋

doi:10.11883/1001-1455(2017)05-0844-09

液滴对爆炸冲击波的衰减作用

doi: 10.11883/1001-1455(2017)05-0844-09

刘贵兵^{1, 2},
侯海量^1, ,,
朱锡¹,
张国栋¹

1.
海军工程大学舰船工程系，湖北武汉 430033
2.
中国人民解放军92941部队，辽宁葫芦岛 125001

基金项目:

国家自然科学基金项目 51209211

国家自然科学基金项目 51479204

详细信息

作者简介:
刘贵兵(1992—)，男，硕士研究生

通讯作者:
侯海量, hou9611104@163.com

中图分类号: O344.7
计量
- 文章访问数: 4525
- HTML全文浏览量: 1296
- PDF下载量: 402
- 被引次数: 0
出版历程
- 收稿日期: 2016-01-25
- 修回日期: 2017-07-08
- 刊出日期: 2017-09-25

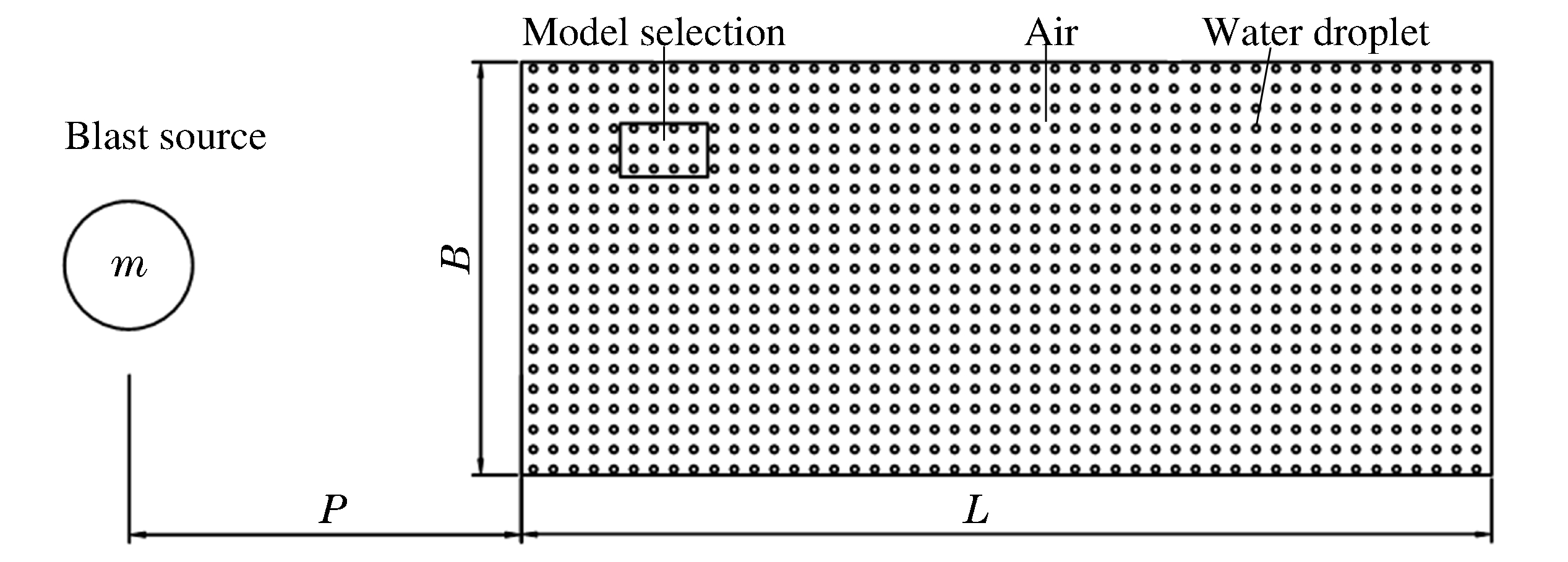
Attenuation of shock wave passing through liquid droplets

Liu Guibing^{1, 2},
Hou Hailiang^{1
, ,},
Zhu Xi¹,
Zhang Guodong¹

1.
Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China
2.
Unit 92941 of Chinese People's Liberation Army, Huludao 125001, Liaoning, China

摘要

摘要: 为分析液滴对舰船舱内爆炸冲击波的耗散与衰减作用，通过有限元分析方法，建立冲击波作用于不同尺寸单个液滴和多排液滴的模型，分析冲击波与单个及多个液滴的作用过程及液滴形态变化，对冲击波衰减规律进行分析总结。得到结论如下：单个液滴模型中，小液滴破碎更迅速，破碎的规律性强；大液滴抛撒现象发生较早，抛撒出的小液滴数目多，但整体变化规律性偏差；不同尺寸单个液滴对冲击波有一定的衰减作用，衰减率随液滴尺寸增大而增大，线性规律较明显；成排液滴对冲击波有明显的衰减作用，相同液滴密度下衰减率随着液滴数量的增多而增大，呈现明显的线性特性。
- 冲击波 /
- 液滴破碎 /
- 比冲量 /
- 环流
Abstract: To characterize the function of water droplets in the restraining and attenuation of the explosive shock wave inside of a cabin, we built several models of a sing layer in z-axis with different sizes of a single droplet and rows of droplets using numerical simulation, analyzed the shock wave interacting with them, observed the interaction process and the change of the droplet forms, summarized the shock wave's attenuation regularities, and obtained some conclusions. The results show that, in the single droplet model, smaller droplets were broken more rapidly and regularly, while bigger droplets tend to break out little droplets more and earlier but less regularly on the whole; that single droplets of different sizes had an effect of attenuation on the shock wave, with an obvious correlation between the increase of the droplet size and that of the attenuation; and that the rows had the most obvious effect of attenuation on the shock wave, with a linear relation between the increase of the droplet number and that of attenuation effect at the same droplet density.
- shock wave /
- droplet broken /
- specific impulse /
- vortex pair

HTML全文

图 1 水雾抑爆宏观模型

Figure 1. Macromodel of mist explosion suppression

下载: 全尺寸图片幻灯片

图 2 单个液滴微元模型

Figure 2. Micromodel of single droplet

下载: 全尺寸图片幻灯片

图 3 多排液滴模型

Figure 3. Micromodel of multi-row droplets

下载: 全尺寸图片幻灯片

图 4 各尺寸液滴5 μs时刻的压力场

Figure 4. Pressure waves of several droplets at 5 μs

下载: 全尺寸图片幻灯片

图 5 各尺寸液滴10 μs时刻的压力场

Figure 5. Pressure waves of several droplets at 10 μs

下载: 全尺寸图片幻灯片

图 6 各尺寸液滴15 μs时刻的压力场

Figure 6. Pressure waves of several droplets at 15 μs

下载: 全尺寸图片幻灯片

图 7 各尺寸液滴10 μs时刻的形态

Figure 7. Forms of several droplets at 10 μs

下载: 全尺寸图片幻灯片

图 8 各尺寸液滴的形态变化

Figure 8. Form change processes of several droplets

下载: 全尺寸图片幻灯片

图 9 测量的压力曲线

Figure 9. Measured pressure curves

下载: 全尺寸图片幻灯片

图 10 无液滴压力曲线

Figure 10. Pressure curves without droplet

下载: 全尺寸图片幻灯片

图 11 成排液滴的压力场变化

Figure 11. Pressure wave change processes of rows of droplets

下载: 全尺寸图片幻灯片

图 12 成排液滴的形态变化

Figure 12. Form change processes of rows of droplets

下载: 全尺寸图片幻灯片

图 13 测量的压力曲线

Figure 13. Measured pressure curves

下载: 全尺寸图片幻灯片

表 1 计算工况

Table 1. Working condition of calculations

r/m	m_e/kg	/(m·kg^-1/3)	Δp_m/MPa	t₊/ms	v/(m·s^-1)	Ma
2.0	100	0.431	5.821	4.113 2	2 350.5	6.913
0.2	0.1	0.431	5.821	0.411 3	2 350.5	6.913

下载: 导出CSV

表 2 比冲量数据

Table 2. Data of specific impluse

t/μs	I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)
t/μs	1 mm		2 mm		4 mm		6 mm		8 mm		无液滴
25	32.21	0.21	30.81	4.55	28.63	11.29	26.60	17.58	24.33	24.61	32.28
30	44.85	2.83	43.24	6.32	40.46	12.34	38.08	17.49	35.35	23.40	46.15
35	54.11	2.11	52.09	5.77	49.32	10.78	47.07	14.84	43.94	20.51	55.28
40	61.06	0.71	59.23	3.67	56.73	7.75	54.40	11.54	51.27	16.63	61.49
40.8	61.97	0.57	60.31	3.24	57.81	7.24	55.49	10.98	52.62	15.57	62.33

下载: 导出CSV

表 3 各模型衰减率

Table 3. Attenuation rate of models

t₊/μs	I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)
t₊/μs	1 mm		2 mm		4 mm		6 mm		8 mm		无液滴
40.8	261.07	0.14	259.41	0.77	256.91	1.73	254.59	2.62	251.72	3.71	261.43

下载: 导出CSV

表 4 比冲量数据

Table 4. Data of specific impluse

t/μs	I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)
t/μs	1排		2排		3排		4排		无液滴
20	9.61	19.10	8.23	30.70	6.64	44.06	5.17	56.44	11.87
25	25.66	20.48	21.93	32.06	19.23	40.42	15.10	53.21	32.28
30	39.76	13.84	34.91	24.35	31.13	32.56	24.89	46.07	46.15
35	48.12	12.95	42.18	23.69	38.79	29.82	32.61	41.01	55.28
40	54.33	11.65	47.85	22.18	43.69	28.95	38.52	37.36	61.49

下载: 导出CSV

表 5 各模型衰减率

Table 5. Attenuation rate of models

t₊/μs	I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)δ/%		I/(N·s·m^-2)
t₊/μs	1排		2排		3排		4排		无液滴
40	253.43	2.75	246.95	5.23	242.79	6.83	237.62	8.82	260.59

下载: 导出CSV

参考文献(15)

[1]	侯海量, 朱锡, 梅志远.舱内爆炸载荷及舱室板架结构的失效模式分析[J].爆炸与冲击, 2007, 27(2):151-158. doi: 10.11883/1001-1455(2007)02-0151-08 Hou Hailiang, Zhu Xi, Mei Zhiyuan. Study on the blast load and failure mode of ship structure subject to internal explosion[J]. Explosion and Shock Waves, 2007, 27(2):151-158. doi: 10.11883/1001-1455(2007)02-0151-08
[2]	朱锡, 张振华, 刘润泉, 等.水面舰艇舷侧防雷舱结构模型抗爆试验研究[J].爆炸与冲击, 2004, 24(2):133-139. http://www.bzycj.cn/article/id/9932 Zhu Xi, Zhang Zhenhua, Liu Runquan, et al. Experimental study on the explosion resistance of cabin near shipboard of surface warship subjected to underwater contact explosion[J]. Explosion and Shock Waves, 2004, 24(2):133-139. http://www.bzycj.cn/article/id/9932
[3]	徐定海, 盖京波, 王善.防护模型在接触爆炸作用下的破坏[J].爆炸与冲击, 2008, 28(5):476-480. doi: 10.11883/1001-1455(2008)05-0476-05 Xu Dinghai, Gai Jingbo, Wang Shan, et al. Deformation and failure of layered defense models subjected to contact explosive load[J]. Explosion and Shock Waves, 2008, 28(5):476-480. doi: 10.11883/1001-1455(2008)05-0476-05
[4]	Radford D D, McShane G J, Deshpande V S, et al. The response of clamped sandwich plates with metallic foam cores to simulated blast loading[J]. International Journal of Solids and Structures, 2006, 43(7):2243-2259. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c0f89ee6c67dd0ac5818c98b646631e8
[5]	Fleck N A, Deshpande V S. The resistance of clamped sandwich beams to shock loading[J]. Journal of Applied Mechanics, 2004, 71(3):386-401. doi: 10.1115/1.1629109
[6]	张旭红, 王志华, 赵隆茂.爆炸载荷作用下铝蜂窝夹芯板的动力响应[J].爆炸与冲击, 2009, 29(4):356-360. doi: 10.11883/1001-1455(2009)04-0356-05 Zhang Xuhong, Wang Zhihua, Zhao Longmao. Dynamic responses of sandwich plate swith aluminum honey combcores subjected[J]. Explosion and Shock Waves, 2009, 29(4):356-360. doi: 10.11883/1001-1455(2009)04-0356-05
[7]	赵凯.分层防护层对爆炸波的衰减和弥散作用研究[D].合肥: 中国科学技术大学, 2007.
[8]	樊自建, 沈兆武, 马宏昊, 等.空气隔层对水中冲击波衰减效果的实验研究[J].中国科学技术大学学报, 2007, 37(10):1306-1311. doi: 10.3969/j.issn.0253-2778.2007.10.025 Fan Zijian, Shen Zhaowu, Ma Honghao, et al. Experimental study on attenuation of underwater shock wave by air interlayer[J]. Journal of University of Science and Technology of China, 2007, 37(10):1306-1311. doi: 10.3969/j.issn.0253-2778.2007.10.025
[9]	姚熊亮, 杨文山, 初文华, 等.水中空气隔层衰减冲击波性能研究[J].高压物理学报, 2011, 25(2):165-172. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gywlxb201102013 Yao Xiongliang, Yang Wenshan, Chu Wenhua, et al. Research on performance of the underwater air-buffer weakening shock wave[J]. Chinese Journal of High Pressure Physics, 2011, 25(2):165-172. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gywlxb201102013
[10]	赵汉中.在封闭结构中水对爆炸冲击波的削波、减压作用[J].爆炸与冲击, 2002, 22(3):252-256. http://www.bzycj.cn/article/id/10157 Zhao Hanzhong. Water mitigation effects on explosions in confined chambers[J]. Explosion and Shock Waves, 2002, 22(3):252-256. http://www.bzycj.cn/article/id/10157
[11]	刘谋斌, 宗智.水幕减爆防护技术数值仿真[J].应用科技, 2010, 37(9):36-41. doi: 10.3969/j.issn.1009-671X.2010.09.008 Liu Moubin, Zong Zhi. Numerical simulation of water mitigation of blasting effects[J]. Applied Science and Technology, 2010, 37(9):36-41. doi: 10.3969/j.issn.1009-671X.2010.09.008
[12]	Jourdan G, Biamino L, Mariani L. Attenuation of a shock wave passing through a cloud of water droplets[J]. Shock Waves, 2010, 20(4):285-296. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c5344bf750dc37608d90488d10030de6
[13]	侯海量, 张成亮, 朱锡, 等.冲击波和高速破片联合作用下夹芯复合舱壁结构的毁伤特性[J].爆炸与冲击, 2015, 35(1):116-123. doi: 10.11883/1001-1455(2015)01-0116-08 Hou Hailiang, Zhang Chengliang, Zhu Xi, et al. Damage characteristics of sandwich bulkhead under the impact of shock and high-velocity fragments[J]. Explosion and Shock Waves, 2015, 35(1):116-123. doi: 10.11883/1001-1455(2015)01-0116-08
[14]	孙叶斌.爆炸作用与装药设计[M].北京:国防工业出版社, 1987.
[15]	朱锡, 张振华, 梅志远, 等.舰船结构毁伤力学[M].北京:国防工业出版社, 2013.