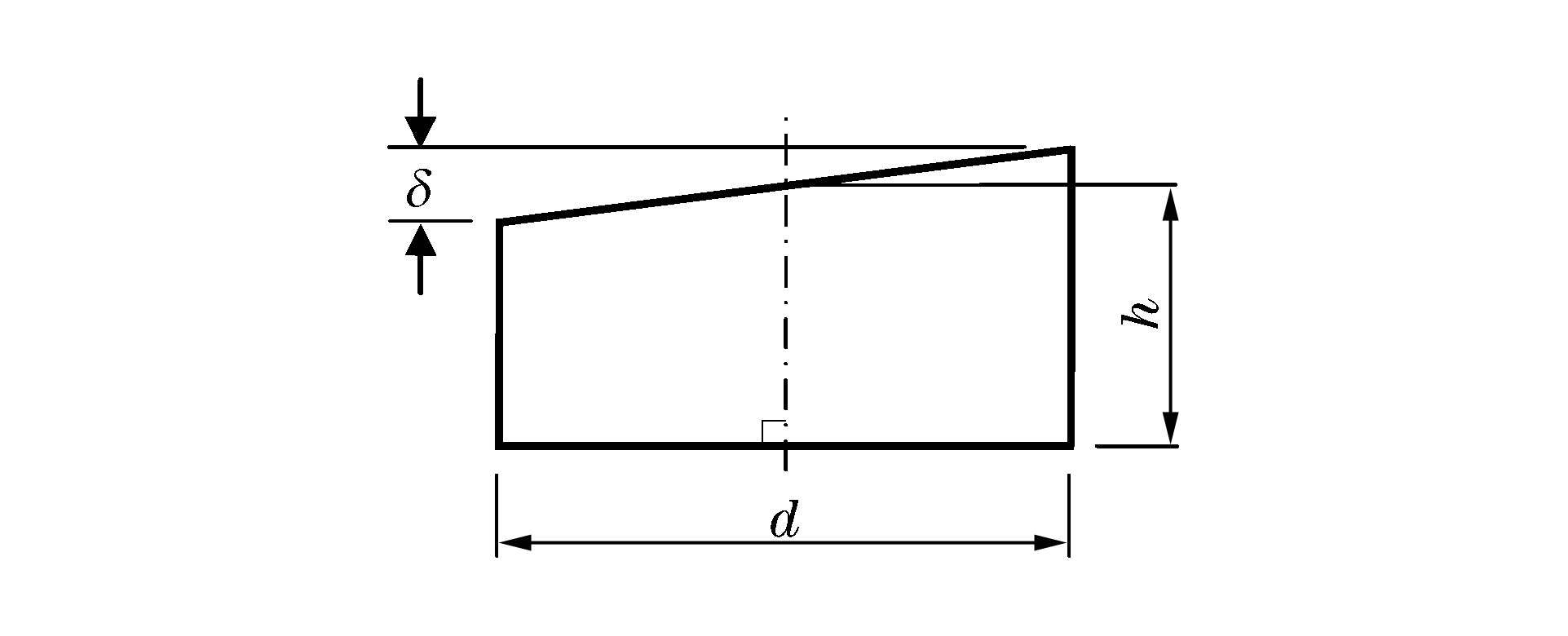
Correction of non-parallel end-faces of rock specimens in SHPB tests
-
摘要: 为研究短圆柱体岩石试件端面不平行对岩石动力学特性测试结果的影响,采用有限元分析软件LS-DYNA对9种端面不平行度和5种杨氏模量的岩石试件开展SHPB(split Hopkinson pressure bar)试验数值模拟,对岩石选用HJC(Holmquist-Johnson-Cook)本构模型。数值模拟结果表明,当端面不平行度在0.40%以内时,端面不平行对动态应力测试结果的影响可忽略不计;但对动态应变测试结果的影响较大。当杨氏模量一定时,平均应变率测试误差和峰值应变测试误差随端面不平行度增大呈线性增大;当端面不平行度一定时,平均应变率测试误差和峰值应变测试误差随杨氏模量增大也呈线性增大。对数值模拟得到的平均应变率测试误差和峰值应变测试误差实施二元线性回归分析,提出了SHPB试验中端面不平行岩石试件平均应变率和峰值应变的修正公式。Abstract: To investigate the influence of a non-parallel end-face for a short cylinder rock specimen on dynamic mechanical test results, we carried out numerical simulation of the SHPB test for rock material in 9 non-parallelisms and 5 Young's moduli using the finite element analysis software LS-DYNA, with the HJC constitutive model chosen for the rock material. The numerical simulation results show that when the non-parallelism of the rock specimen end-face is below 0.40%, the influence of the non-parallel end-face on the dynamic stress test results is negligible, while the influence of the non-parallel end-face on the dynamic strain test results is much bigger. When the Young's modulus remains the same, there is an approximately linear relation between the test error of the average strain rate and the non-parallelism or between the test error of the peak strain and the non-parallelism. When the non-parallelism remains the same, there is also an approximately linear relation between the test error of the average strain rate and the Young's modulus or between the test error of the peak strain and the Young's modulus. After conducting the binary linear regression analysis for the test error of the average strain rate and the test error of the peak strain obtained from numerical simulation, a correction formula for the average strain rate and the peak strain is proposed for the SHPB test of non-parallel end-face rock specimens.
-
Key words:
- rock /
- SHPB /
- non-parallelism /
- strain rate /
- peak strain /
- error
-
表 1 不同端面不平行岩石试件SHPB数值模拟结果
Table 1. Numerical simulation results of rock specimens in various non-parallelisms
γ/% σd/MPa $\dot \varepsilon $/s-1 εu σd/MPa $\dot \varepsilon $/s-1 εu σd/MPa $\dot \varepsilon $/s-1 εu σd/MPa $\dot \varepsilon $/s-1 εu σd/MPa $\dot \varepsilon $/s-1 εu E=14 GPa E=21 GPa E=28 GPa E=35 GPa E=42 GPa 0.00 220.93 117.8 0.018 4 228.30 95.6 0.014 2 229.85 82.9 0.011 9 230.94 74.3 0.010 5 231.59 68.4 0.009 5 0.05 220.55 119.8 0.018 6 228.02 97.6 0.014 4 229.74 84.7 0.012 2 230.33 76.1 0.010 8 230.33 70.5 0.009 7 0.10 220.67 121.3 0.018 8 227.01 98.9 0.014 7 229.11 86.8 0.012 3 229.91 77.9 0.011 1 229.69 72.1 0.010 0 0.15 219.90 124.8 0.018 7 226.47 101.8 0.014 8 228.94 88.7 0.012 6 229.88 80.3 0.011 2 229.89 74.5 0.010 1 0.20 219.85 125.7 0.019 1 225.90 103.2 0.015 1 228.99 90.5 0.012 8 229.87 81.9 0.011 5 230.59 76.4 0.010 4 0.25 219.56 127.8 0.019 3 225.86 106.1 0.015 2 228.33 92.3 0.013 2 229.77 84.3 0.011 7 230.29 78.3 0.010 7 0.30 218.78 128.6 0.019 7 224.82 107.2 0.015 5 227.83 94.5 0.013 3 229.98 85.8 0.012 0 229.85 80.1 0.011 0 0.35 216.98 131.4 0.019 7 223.63 109.6 0.015 7 226.45 96.3 0.013 6 229.62 87.6 0.012 3 230.18 81.7 0.011 4 0.40 214.73 132.6 0.020 2 221.08 111.0 0.016 1 224.64 98.3 0.013 9 228.11 89.1 0.012 7 228.87 83.3 0.011 8 表 2 5种杨氏模量岩石试件端面不平行度的上限
Table 2. Upper limit of non-parallelism for rock specimens in five kinds of Young's moduli
E/GPa γup/% δup/mm 14 0.40 0.100 0 21 0.35 0.087 5 28 0.30 0.075 0 35 0.25 0.062 5 42 0.25 0.062 5 表 3 端面不平行岩石试件动态应变测试结果的修正
Table 3. Corrected dynamic strain test results of non-parallel end-face rock specimens
γ/% $\dot \varepsilon $mod/s-1 εu, mod $\dot \varepsilon $mod/s-1 εu, mod $\dot \varepsilon $mod/s-1 εu, mod $\dot \varepsilon $mod/s-1 εu, mod $\dot \varepsilon $mod/s-1 εu, mod E=14 GPa E=21 GPa E=28 GPa E=35 GPa E=42 GPa 0.00 117.8 0.018 4 95.6 0.014 2 82.9 0.011 9 74.3 0.010 5 68.4 0.009 5 0.05 119.7 0.018 9 96.4 0.014 3 82.7 0.012 0 73.5 0.010 5 67.4 0.009 2 0.10 118.6 0.018 7 95.6 0.014 3 83.0 0.011 9 73.7 0.010 5 67.4 0.009 3 0.15 119.4 0.018 3 96.3 0.014 1 83.0 0.011 9 74.3 0.010 4 68.2 0.009 3 0.20 117.7 0.018 3 95.6 0.014 1 82.9 0.011 9 74.3 0.010 5 68.6 0.009 4 0.25 117.2 0.018 1 96.3 0.013 9 82.9 0.012 0 74.9 0.010 5 68.9 0.009 5 0.30 115.5 0.018 1 95.3 0.013 9 83.2 0.011 9 74.8 0.010 6 69.1 0.009 5 0.35 115.7 0.017 8 95.5 0.013 9 83.1 0.011 9 74.9 0.010 6 69.1 0.009 7 0.40 114.5 0.017 9 94.9 0.014 0 83.2 0.012 0 74.7 0.010 8 69.2 0.009 9 -
[1] 胡时胜, 王礼立, 宋力, 等.Hopkinson压杆技术在中国的发展回顾[J].爆炸与冲击, 2014, 34(6):641-657. doi: 10.11883/1001-1455(2014)06-0641-17Hu Shisheng, Wang Lili, Song Li, et al. Review of the development of Hopkinson pressure bar technique in China[J]. Explosion and Shock Waves, 2014, 34(6):641-657. doi: 10.11883/1001-1455(2014)06-0641-17 [2] 袁璞, 马芹永.干湿循环条件下煤矿砂岩分离式霍普金森压杆试验研究[J].岩土力学, 2013, 34(9):2557-2562. http://d.old.wanfangdata.com.cn/Periodical/ytlx201309019Yuan Pu, Ma Qinyong. Split Hopkinson pressure bar tests on sandstone in coalmine under cyclic wetting and drying[J]. Rock and Soil Mechanics, 2013, 34(9):2557-2562. http://d.old.wanfangdata.com.cn/Periodical/ytlx201309019 [3] 王世鸣, 李夕兵, 宫凤强, 等.静载和动载下不同龄期混凝土力学特性的试验研究[J].工程力学, 2013, 30(2):143- 149. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201302021Wang Shiming, Li Xibing, Gong Fengqiang, et al.Experimental study on mechanical properties of different ages concrete under static and dynamic load[J]. Engineering Mechanics, 2013, 30(2):143-149. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201302021 [4] 段士伟, 李永池, 李平.陶瓷材料SHPB实验的改进垫块法[J].实验力学, 2013, 28(5):607-613. http://d.old.wanfangdata.com.cn/Periodical/sylx201305009Duan Shiwei, Li Yongchi, Li Ping. An improved inserts form in SHPB experiment for ceramic material[J]. Journal of Experimental Mechanics, 2013, 28(5):607-613. http://d.old.wanfangdata.com.cn/Periodical/sylx201305009 [5] 袁璞, 徐颖.养护时间对胶结砂相似模型材料抗压性能的影响[J].振动与冲击, 2015, 34(13):200-204. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201513035.htmYuan Pu, Xu Ying. Influence of curing time on compressive properties of cemented sand similar materials[J]. Journal of Vibration and Shock, 2015, 34(13):200-204. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201513035.htm [6] 马芹永, 袁璞, 陈文峰, 等.人工冻土单轴与围压状态动力学性能对比分析[J].地下空间与工程学报, 2014, 10(1): 26-29. http://d.old.wanfangdata.com.cn/Periodical/dxkj201401005Ma Qinyong, Yuan Pu, Chen Wenfeng, et al. Comparative analysis on dynamic mechanical properties of artificial frozen soil under uniaxial load and confining pressure[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(1):26-29. http://d.old.wanfangdata.com.cn/Periodical/dxkj201401005 [7] 王礼立.应力波基础[M].2版.北京:国防工业出版社, 2010:52-60. [8] 陶俊林, 陈裕泽, 田常津, 等.SHPB系统圆柱试件的惯性效应分析[J].固体力学学报, 2005, 26(1):107-110. doi: 10.3969/j.issn.0254-7805.2005.01.019Tao Junlin, Chen Yuze, Tian Changjin, et al. Analysis of the inertial effect of the cylindrical specimen in SHPB system[J]. Acta Mechanica Solida Sinica, 2005, 26(1):107-110. doi: 10.3969/j.issn.0254-7805.2005.01.019 [9] 卢玉斌, 宋丹路, 李庆明, 等.分离式霍普金森压杆试验中工程材料断面摩擦模型的确定[J].振动与冲击, 2012, 31(3):18-22. doi: 10.3969/j.issn.1000-3835.2012.03.004Lu Yubin, Song Danlu, Li Qingming, et al. Interface friction model in split Hopkinson pressure bar tests for engineering materials[J]. Journal of Vibration and Shock, 2012, 31(3):18-22. doi: 10.3969/j.issn.1000-3835.2012.03.004 [10] 张祖根, 李英雷, 李英华, 等.压杆/试样表面接触变形对SHPB实验应变测量的影响[J].爆炸与冲击, 2009, 29(6): 573-578. doi: 10.3321/j.issn:1001-1455.2009.06.003Zhang Zugen, Li Yinglei, Li Yinghua, et al. Influence of bar/specimen contact surfaces' indentation on strain measurement in SHPB experiments[J]. Explosion and Shock Waves, 2009, 29(6):573-578. doi: 10.3321/j.issn:1001-1455.2009.06.003 [11] 宋力, 胡时胜.SHPB实验中的端面凹陷修正[J].爆炸与冲击, 2010, 30(2):203-208. doi: 10.11883/1001-1455(2010)02-0203-06Song Li, Hu Shisheng. Correction of end-face indentation in SHPB test[J]. Explosion and Shock Waves, 2010, 30(2):203-208. doi: 10.11883/1001-1455(2010)02-0203-06 [12] Zhou Y X, Xia K, Li X B, et al. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 49:105-112. doi: 10.1016/j.ijrmms.2011.10.004 [13] 中国国家标准化管理委员会.煤与岩石物理力学性质测定方法: 第7部分: 单轴抗压强度测定及软化系数计算方法: GB/T 23561.7-2009[S].北京: 中国质检出版社, 2009. [14] 果春焕, 周培俊, 陆子川, 等.波形整形技术在Hopkinson杆实验中的应用[J].爆炸与冲击, 2015, 35(6):881-887. doi: 10.11883/1001-1455(2015)06-0881-07Guo Chunhuan, Zhou Peijun, Lu Zichuan, et al. Application of pulse shaping technique in Hopkinson bar experiment[J]. Explosion and Shock Waves, 2015, 35(6):881-887. doi: 10.11883/1001-1455(2015)06-0881-07 [15] 赵光明, 马文伟, 孟祥瑞.动载作用下岩石类材料破坏模式及能量特性[J].岩土力学, 2015, 36(12):3598-3605. http://d.old.wanfangdata.com.cn/Periodical/ytlx201512033Zhao Guangming, Ma Wenwei, Meng Xiangrui. Damage modes and energy characteristics of rock-like materials under dynamic load[J]. Rock and Soil Mechanics, 2015, 36(12):3598-3605. http://d.old.wanfangdata.com.cn/Periodical/ytlx201512033 [16] 方秦, 孔祥振, 吴昊, 等.岩石Holmquist-Johnson-Cook模型参数的确定方法[J].工程力学, 2014, 31(3):197-204. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201403027Fang Qin, Kong Xiangzhen, Wu Hao, et al. Determination of Holmquist-Johnson-Cook constitutive model parameters of rock[J]. Engineering Mechanics, 2014, 31(3):197-204. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201403027 [17] 宋力, 胡时胜.SHPB数据处理中的二波法与三波法[J].爆炸与冲击, 2005, 25(4):368-373. doi: 10.3321/j.issn:1001-1455.2005.04.014Song Li, Hu Shisheng. Two-wave and three-wave method in SHPB data processing[J]. Explosion and Shock Waves, 2005, 25(4):368-373. doi: 10.3321/j.issn:1001-1455.2005.04.014 [18] 刘婷婷, 李建春, 李海波, 等.接触面积对波传播规律及节理力学特性影响[J].岩石力学与工程学报, 2014, 33(9): 1749-1755. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb201409003Liu Tingting, Li Jianchun, Li Haibo, et al. Effects of contact area on stress wave propagation and joint mechanical properties[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9):1749-1755. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb201409003 -







 下载:
下载: