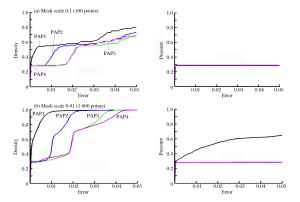
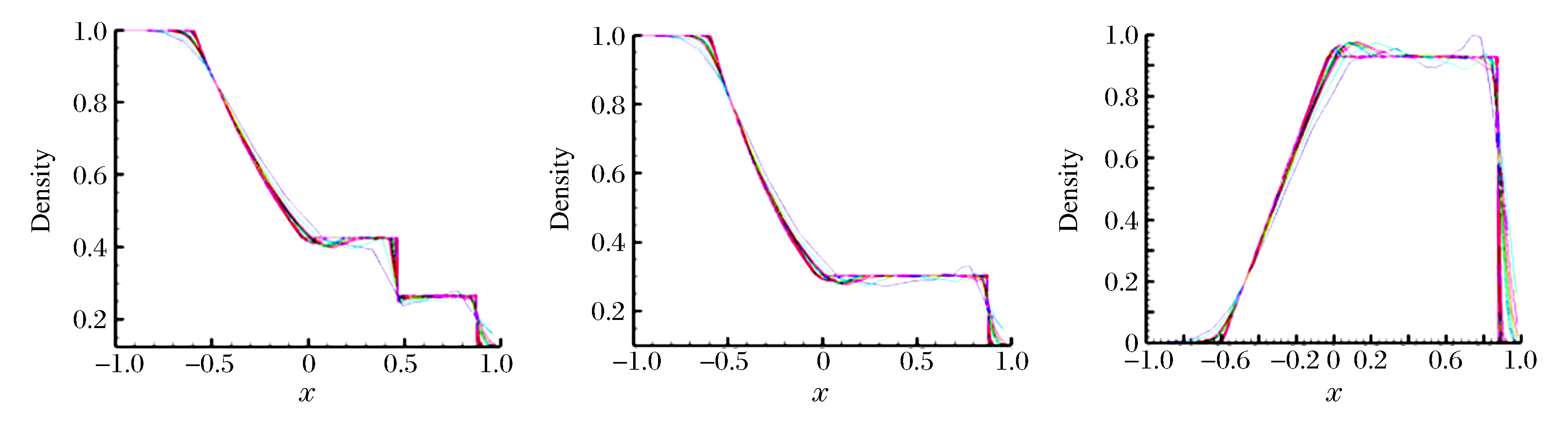
Confidence level of numerical simulation of detonation through quantifying the horsetail of error
-
摘要: 针对爆轰流体力学数值模拟过程中输入参数的不确定性, 通过抽样技术, 形成确定性爆轰流体力学程序的各种输入和数值求解, 建立输入参数与输出响应量的样本, 再通过概率框架下的误差累积分布函数与马尾图, 给出了爆轰数值模拟过程中输入参数不确定度对模拟结果影响的置信度量化方法。通过一维黎曼问题、平面爆轰问题计算了误差马尾图, 给出了二维爆轰拉氏自适应流体动力学LAD2D程序计算网格与模拟结果置信度的关系, 对多物理爆轰过程发展高置信度数值模拟软件有很好的借鉴作用。Abstract: In the present study, sampling technique was used to deal with the input parameter uncertainty in the numerical simulation of detonation CFD(computational fluid dynamics). Then the deterministic detonation CFD program was constructed with different input. The sample of the input parameter and system response quantity was obtained through the previous result. The cumulative distribution function and the horsetail of error was utilized to achieve the confidence level, which was then used to assess the influence of the input parameter uncertainty on the simulation result of detonation CFD. The horsetail graph of error in one dimensional Riemann problem and planar detonation problem were presented to analyze the relationship between the confidence level of simulation result and the mesh used in LAD2D. This method provides a reference for developing the software of multi-physics detonation process on high confidence level.
-
表 1 JWL状态方程4套参数
Table 1. Four sets of parameters for JWL state eqution
参数代号 A/GPa B/GPa R1 R2 ω PAP1 765.788 14.249 4.3 1.45 0.28 PAP2 947.774 59.206 5.0 2.00 0.28 PAP2 1 502.851 134.913 6.3 2.40 0.28 PAP3 3 250.433 233.271 8.2 2.80 0.28 -
[1] 王瑞利, 林忠, 温万治, 等.多介质拉氏自适应流体动力学软件LAD2D研制及其应用[J].计算机辅助工程, 2014, 23(2):1-7. http://d.old.wanfangdata.com.cn/Periodical/jsjfzgc201402001Wang Ruili, Lin Zhong, Wen Wanzhi, et al.Development and application of adaptive multi-media Lagrangian fluid dynamics software LAD2D[J].Computer Aided Engineering, 2014, 23(2):1-7. http://d.old.wanfangdata.com.cn/Periodical/jsjfzgc201402001 [2] 王瑞利, 温万治.复杂工程建模与模拟的验证与确认[J].计算机辅助工程, 2014, 23(4):61-68. http://d.old.wanfangdata.com.cn/Conference/8538180Wang Ruili, Wen Wanzhi.Advances in verification and validation of modeling and simulation of the complex engineering[J].Computer Aided Engineering, 2014, 23(4):61-68. http://d.old.wanfangdata.com.cn/Conference/8538180 [3] Wang Ruili, Liang Xiao, Lin Wenzhou, et al.Verification and validation of the detonation computational fluid dynamics model[J].Defect and Diffusion Forum, 2016, 366(3):40-46. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.4028/www.scientific.net/DDF.366.40 [4] Wang Ruili, Zhang Shudao, Liu Quan. One method of constructing manufactured solutions to 2D hydrodynamics Euler equations[C]//Proceedings of the International Conference on Numerical Analysis and Applied Mathematics 2014(ICNAAM-2014), 2015, 1648(1): 599-620. [5] 张冠人, 陈大年.凝聚炸药起爆动力学[M].北京:国防工业出版社, 1991. [6] 孙锦山.凝聚炸药非理想爆轰的数值模拟[J].力学进展, 1995, 25(1):127-133. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CAS201303040000428906Sun Jinshan.Numerical modeling of non-ideal detonation in condensed explosives[J].Advances in Mechanics, 1995, 25(1):127-133. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CAS201303040000428906 [7] 王瑞利, 江松.多物理耦合非线性偏微分方程与数值解不确定性量化数学方法[J].中国科学(数学), 2015, 45(6):723-738. http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK201506001.htmWang R L, Jiang S.Mathematical methods for uncertainty quantification in nonlinear multi-physics systems and their numerical simulations[J].Scientia Sinica (Mathematica), 2015, 45(6):723-738. http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK201506001.htm [8] 王瑞利, 刘全, 温万治.非嵌入式多项式混沌法在爆轰产物JWL参数评估中的应用[J].爆炸与冲击, 2015, 35(1):9-15. http://www.bzycj.cn/CN/abstract/abstract9419.shtmlWang Ruili, Liu Quan, Wen Wanzhi.Non-intrusive polynomial chaos methods and its application in the parameters assessment of explosion product JWL[J].Explosion and Shock Waves, 2015, 35(1):9-15. http://www.bzycj.cn/CN/abstract/abstract9419.shtml [9] 汤涛, 周涛.不确定性量化的高精度数值方法和理论[J].中国科学(数学), 2015, 45(7):891-928. http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK201507006.htmTang Tao, Zhou Tao.Recent developments in high order numerical methods for uncertainty quantification[J].Scientia Sinica (Mathematica), 2015, 45(7):891-928. http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK201507006.htm [10] 王瑞利, 林忠, 魏兰.利用前沿推进法计算复杂炸药结构的起爆时间[J].高压物理学报, 2015, 29(4):286-292. http://www.cnki.com.cn/Article/CJFDTOTAL-GYWL201504009.htmWang Ruili, Lin Zhong, Wei Lan.Calculating the initiation time of the explosive with complex structure using the advancing front technique[J].Chinese Journal of High Pressure Physics, 2015, 29(4):286-292. http://www.cnki.com.cn/Article/CJFDTOTAL-GYWL201504009.htm [11] 恽寿榕, 赵衡阳.爆炸力学[M].北京:国防工业出版社, 2005. -







 下载:
下载: