Influence of free surface on energy distribution characteristics of blasting vibration
-
摘要: 基于爆破振动实测数据, 通过小波分析方法, 得到不同数量自由面爆破振动信号的总能量、各频带的峰值质点振动速度(PPV)及各频带能量, 进而对不同数量自由面爆破振动信号的能量分布特性进行研究。结果表明:开(掏)槽爆破, 由于受单一自由面限制, 大部分炸药爆炸的能量都将作为地震能量消耗掉;自由面越多, 爆破振动信号总能量越少;自由面的数量可影响各频带振动分量分布, 随自由面数量的增加, 爆破振动能量更趋向高频分布, 中低频能量有减少趋势, 振动速度降低;同一振动信号中的高频带PPV虽比低频带PPV高, 但振动持续时间短, 能量衰减较快。建议在工程爆破的减振设计中, 优化起爆方案, 尽量利用多个自由面, 这将比仅仅减少单段起爆药量更有效。Abstract: In combination with the measured data of the blasting vibration, the total energy, the frequency band energy, and the PPV of each band of the blasting vibration signal with different numbers of free surfaces were obtained using the wavelet analysis. Then the energy distribution characteristics of the blasting vibration signal with different numbers of free surfaces were studied. The results show that the slotted blasting or cut blasting is restricted by a single free surface, thus most of the energy of the explosion will be consumed as seismic energy; the greater the number of free surfaces, the less the total energy of the blasting vibration signal; with the increase of the of free surfaces, the distribution of the vibration components of each frequency band can be affected, which makes the blasting vibration energy more tend to be the high frequency distribution, so that the energy in the middle and low frequency can be reduced, and the vibration velocity is reduced as well; the PPV of the high frequency band is higher than that of the low frequency band, but the duration of the vibration is shorter, and the energy attenuation is faster in the same vibration signal. It is suggested that, in the design of reducing the blasting vibration, it is more effective to optimize the initiation scheme by using as many free surfaces as possible than by merely reducing the single segment of detonating charge.
-
表 1 不同数量自由面及不同测点爆破振动信号的条件
Table 1. Blasting vibration of different numbers of free surfaces and different test points
信号 1-1 1-2 2-1 2-2 1-a 1-b 1-c 2-a 2-b 2-c 爆心距/m 248 248 239 239 248 445 612 239 434 603 各分段药量/kg 82 69 200 200 82 82 82 200 200 200 自由面数 1 2 2 3 1 1 1 2 2 2 表 2 爆破振动信号1-1~2-2的能量分布
Table 2. Energy distribution of blasting vibration signal (1-1~2-2)
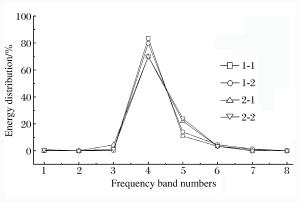
频带数 频带/Hz 小波频带能量/(mm·s-1)2 信号1-1 信号1-2 信号2-1 信号2-2 1 0~7.812 5 8.346 7 0.042 3 0.063 7 1.001 4 2 7.812 5~15.625 0.060 8 0.058 8 0.264 8 0.042 0 3 15.625~31.25 15.662 8 0.068 0 32.258 6 1.603 5 4 31.25~62.5 1 935.475 0 86.858 2 498.663 8 78.855 8 5 62.5~125 254.442 1 15.230 0 156.725 0 27.077 5 6 125~250 78.738 2 5.010 9 23.780 6 3.863 1 7 250~500 21.978 5 1.543 2 0.337 7 0.148 6 8 500~100 0 2.879 2 0.025 4 0.018 0 0.009 6 总和 2 317.538 108.836 8 712.112 2 112.601 5 表 3 爆破振动信号1-a~1-c和2-a~2-c的能量分布
Table 3. Energy distribution of blasting vibration signal (1-a~1-c) and (2-a~2-c)
频带数 频带/Hz 小波频带能量/(mm·s-1)2 信号1-a 信号2-a 信号1-b 信号2-b 信号1-c 信号2-c 1 0~7.812 5 8.346 7 0.063 7 0.045 8 0.152 6 0.071 8 0.290 1 2 7.812 5~15.625 0.060 8 0.264 8 0.331 7 0.182 6 0.063 5 0.339 6 3 15.625~31.25 15.662 8 32.258 6 6.387 8 1.975 1 4.746 5 1.235 7 4 31.25~62.5 1 935.475 0 498.663 8 5.201 0 1.205 0 33.687 2 14.729 6 5 62.5~125 254.442 1 156.725 0 45.034 0 5.292 8 5.801 9 2.264 4 6 125~250 78.738 2 23.780 6 70.436 7 12.685 3 4.169 1 0.593 8 7 250~500 21.978 5 0.337 7 4.837 9 0.202 2 0.351 3 0.030 7 8 500~1 000 2.879 2 0.018 0 0.016 4 0.011 3 0.014 1 0.013 3 总和 2 317.538 712.112 2 132.291 3 21.706 9 48.905 4 19.497 -
[1] 王丹丹, 池恩安, 詹振锵, 等.自由面状态对爆破效果的影响及解决措施[J].金属矿山, 2012, 41(3):52-55. doi: 10.3969/j.issn.1001-1250.2012.03.013Wang Dandan, Chi En'an, Zhan Zhenqiang, et al.The Influence of free surface morphology on blasting effect and its solving measurement[J].Metal Mine, 2012, 41(3):52-55. doi: 10.3969/j.issn.1001-1250.2012.03.013 [2] 张志呈, 张顺朝.论工程爆破中自由面与爆破效果的关系[J].西南科技大学学报, 2003, 18(3):30-33. doi: 10.3969/j.issn.1671-8755.2003.03.009Zhang Zhicheng, Zhang Shunchao.On the relationship between the free surface and the blasting effect of engineering blasting[J].Journal of Southwest University of Science and Technology, 2003, 18(3):30-33. doi: 10.3969/j.issn.1671-8755.2003.03.009 [3] 陈星明, 肖正学, 蒲传金.自由面对爆破地震强度影响的试验研究[J].爆破, 2009, 26(4):38-41. http://d.old.wanfangdata.com.cn/Periodical/bp200904010Chen Xingming, Xiao Zhengxue, Pu Chuanjin.Experimental study on influence blasting earthquake strength to free faces[J].Blasting, 2009, 26(4):38-41. http://d.old.wanfangdata.com.cn/Periodical/bp200904010 [4] 中国生, 徐国元, 熊正明.基于小波变换的爆破地震信号能量分析法的应用研究[J].爆炸与冲击, 2006, 26(3):222-227. doi: 10.3321/j.issn:1001-1455.2006.03.005Zhong Guosheng, Xu Guoyuan, Xiong Zhengming.Application research of the energy analysis method for blasting seismic signals based on wavelet transform[J].Explosion and Shock Waves, 2006, 26(3):222-227. doi: 10.3321/j.issn:1001-1455.2006.03.005 [5] 中国生. 基于小波变换爆破振动的应用基础研究[D]. 长沙: 中南大学, 2006. [6] 李洪涛, 卢文波, 舒大强.爆破地震波的能量衰减规律研究[J].岩石力学与工程学报, 2010, 29(增刊1):3364-3369. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb2010z1110Li Hongtao, Lu Wenbo, Shu Daqiang.Study of energy attenuation law of blast-induced seismic wave[J].Chinese Journal of Rock Mechanics and Engineering, 2010, 29(suppl 1):3364-3369. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb2010z1110 [7] 晏俊伟, 龙源, 方向.基于小波变换的爆破振动信号能量分布特性分析[J].爆炸与冲击, 2007, 27(5):405-410. doi: 10.3321/j.issn:1001-1455.2007.05.004Yan Junwei, Long Yuan, Fang Xiang.Analysis on features of energy distribution for blasting seismic wave based on wavelet transform[J].Explosion and Shock Waves, 2007, 27(5):405-410. doi: 10.3321/j.issn:1001-1455.2007.05.004 [8] 费鸿禄, 马诺诺.坝基开挖爆破振动频带小波能量分析[J].爆破, 2010, 27(3):99-104. doi: 10.3963/j.issn.1001-487X.2010.03.029Fei Honglu, Ma Nuonuo.Wavelet energy analysis of blasting vibration frequency band on dam foundation excavation[J].Blasting, 2010, 27(3):99-104. doi: 10.3963/j.issn.1001-487X.2010.03.029 [9] 池恩安, 赵明生, 梁开水.自由面数量对爆破地震波时频特性影响分析[J].爆破, 2013, 30(2):16-20. doi: 10.3963/j.issn.1001-487X.2013.02.004Chi En'an, Zhang Mingsheng, Liang Kaishui.Influence of number of free surface on time-frequency characteristics of blasting seismic wave[J].Blasting, 2013, 30(2):16-20. doi: 10.3963/j.issn.1001-487X.2013.02.004 [10] 林大超, 施惠基, 白春华, 等.爆炸地震效应的时频分析[J].爆炸与冲击, 2003, 23(1):31-36. doi: 10.3321/j.issn:1001-1455.2003.01.006Lin Dachao, Shi Huiji, Bai Chunhua, et al.Time-frequency analysis of explosion seismic effects[J].Explosion and Shock Waves, 2003, 23(1):31-36. doi: 10.3321/j.issn:1001-1455.2003.01.006 [11] 中国生, 房营光, 徐国元.基于小波变换的建(构)筑物爆破振动效应评估研究[J].振动与冲击, 2008, 27(8):121-126. doi: 10.3969/j.issn.1000-3835.2008.08.031Zhong Guosheng, Fang Yingguang, Xu Guoyuan.Study on blasting vibration effect assessment of structure based on wavelet transform[J].Journal of Vibration and Shock, 2008, 27(8):121-126. doi: 10.3969/j.issn.1000-3835.2008.08.031 [12] 李夕兵, 张义平.爆破震动信号的小波分析与HHT变换[J].爆炸与冲击, 2005, 25(6):528-535. doi: 10.3321/j.issn:1001-1455.2005.06.008Li Xibin, Zhang Yiping.Wavelet analysis and Hilbert-Huang transform of blasting vibration signal[J].Explosion and Shock Waves, 2005, 25(6):528-535. doi: 10.3321/j.issn:1001-1455.2005.06.008 [13] 凌同华, 李夕兵.多段微差爆破振动信号频带能量分布特征的小波包分析[J].岩石力学与工程学报, 2005, 24(7):1117-1122. doi: 10.3321/j.issn:1000-6915.2005.07.005Ling Tonghua, Li Xibin.Analysis of energy distributions of millisecond blast vibration signals using the wavelet packet method[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7):1117-1122. doi: 10.3321/j.issn:1000-6915.2005.07.005 [14] 马瑞恒, 时党勇.爆破振动信号的时频分析[J].振动与冲击, 2005, 24(4):92-96. doi: 10.3969/j.issn.1000-3835.2005.04.026Ma Ruiheng, Shi Dangyong.Time-frequency analysis of blasting vibration signal[J].Journal of Vibration and Shock, 2005, 24(4):92-96. doi: 10.3969/j.issn.1000-3835.2005.04.026 [15] 娄建武, 龙源, 徐全军.基于小波包技术的爆破地震波特征提取及预报[J].爆炸与冲击, 2004, 24(3):261-267. doi: 10.3321/j.issn:1001-1455.2004.03.011Lou Jianwu, Long Yuan, Xu Quanjun.A study on the extraction and prediction of blasting seismic wave characteristics by wavelet packets technique[J].Explosion and Shock Waves, 2004, 24(3):261-267. doi: 10.3321/j.issn:1001-1455.2004.03.011 [16] 李夕兵, 凌同华, 张义平.爆破震动信号分析理论与技术[M].北京:科学出版社, 2009:23-186. -






 下载:
下载: