CL-20基混合炸药的冲击起爆特征

皮铮迪; 陈朗; 刘丹阳; 伍俊英

doi:10.11883/1001-1455(2017)06-0915-09

CL-20基混合炸药的冲击起爆特征

doi: 10.11883/1001-1455(2017)06-0915-09

北京理工大学爆炸科学与技术国家重点实验室，北京 100081

详细信息

作者简介:
皮铮迪(1984—)，男，博士

通讯作者:
陈朗, chenlang@bit.edu.cn

中图分类号: O381
计量
- 文章访问数: 4672
- HTML全文浏览量: 1495
- PDF下载量: 394
- 被引次数: 0
出版历程
- 收稿日期: 2016-04-26
- 修回日期: 2016-07-26
- 刊出日期: 2017-11-25

Shock initiation of CL-20 based explosives

State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 为了研究CL-20基混合炸药的冲击起爆特征，深入分析冲击波作用下CL-20基混合炸药的爆轰成长规律，采用炸药驱动飞片冲击起爆实验方法，对CL-20、CL-20/NTO和CL-20/FOX-7三种压装混合炸药进行了冲击起爆实验，通过嵌入在炸药内部不同位置处的锰铜压力传感器，获得了炸药内部压力的变化历程。依据实验结果标定了混合炸药的点火增长模型参数，其中，利用反应速率方程中的两个增长项，分别模拟CL-20/NTO和CL-20/FOX-7混合炸药中两种组分的反应增长过程，得到这两种混合炸药的反应速率方程参数。并通过数值模拟的方法得到了三种炸药的临界起爆阈值和POP关系。研究结果表明：三种CL-20基混合炸药中，CL-20/NTO混合炸药具有更高的临界起爆阈值，而CL-20/FOX-7混合炸药具有更长的爆轰成长距离；此外，利用此套拟合双组分混合炸药反应速率方程的方法，可以对新型配方炸药的冲击起爆过程进行预测性计算
- 冲击起爆 /
- CL-20 /
- NTO /
- FOX-7 /
- 点火增长反应速率方程
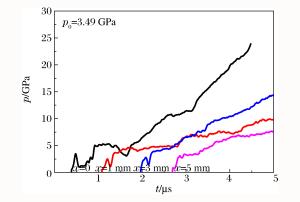
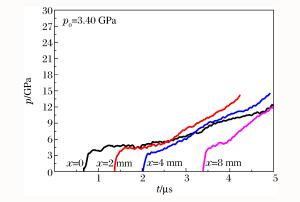
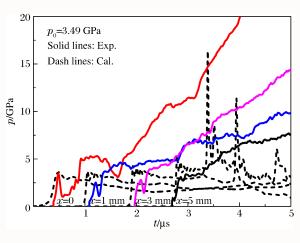
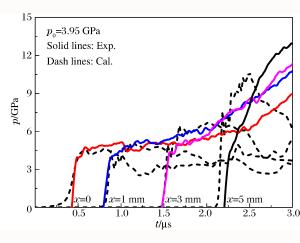
Abstract: In the present work, shock initiation experiments on CL-20, CL-20/NTO and CL-20/FOX-7 mixed explosives were performed to investigate the shock initiation characteristics of Hexanitro-hexaazaisowurtzitane (CL-20) based explosives. An explosive driven flyer device was utilized to initiate the charges with manganin gauges embedded into the target to measure time resolved local pressure histories. The shock initiation of CL-20 based explosives was simulated using the ignition and growth reactive flow model, and the parameters were obtained by fitting the experimental data. Furthermore, the reaction of two compositions in CL-20/NTO and CL-20/FOX-7 was simulated respectively using the two growth terms in the ignition and growth model. The parameters were then applied in the calculation of the initial shock pressure-distance to detonation relationship (Pop plot) and the shock initiation critical thresholds for the three mixed explosives. The results show that the CL-20/NTO explosive has a higher shock initiation critical threshold, while the CL-20/FOX-7 explosive has a longer distance to detonation under the same loading conditions. Besides, this model for the explosive with the two compositions can be applied to predict the shock initiation characteristics of the explosive with new formulations.
- shock initiation /
- CL-20 /
- NTO /
- FOX-7 /
- ignition and growth reactive flow model

HTML全文

图 1 炸药驱动飞片冲击起爆实验装置示意图及照片

Figure 1. Diagram and photo of shock initiation experimental apparatus

下载: 全尺寸图片幻灯片

图 2 CL-20混合炸药在距冲击波入射面不同距离处的内部压力-时间曲线

Figure 2. Pressure curves of CL-20 explosive at different displacements from shock incidence plane

下载: 全尺寸图片幻灯片

图 3 CL-20/NTO混合炸药在距冲击波入射面不同距离处的内部压力-时间曲线

Figure 3. Pressure curves of CL-20/NTO explosive at different displacements from shock incidence plane

下载: 全尺寸图片幻灯片

图 4 CL-20/FOX-7混合炸药在距冲击波入射面不同距离处的内部压力-时间曲线

Figure 4. Pressure curves of CL-20/FOX-7 explosive at different displacements from shock incidence plane

下载: 全尺寸图片幻灯片

图 5 CL-20混合炸药计算与实验结果对比

Figure 5. Experimental and calculated pressure histories in shock initiation of CL-20 explosive

下载: 全尺寸图片幻灯片

图 6 CL-20/NTO混合炸药计算与实验结果对比

Figure 6. Experimental and calculated pressure histories in shock initiation of CL-20/NTO

下载: 全尺寸图片幻灯片

图 7 CL-20/FOX-7混合炸药计算与实验结果对比

Figure 7. Experimental and calculated pressure histories in shock initiation of CL-20/FOX-7

下载: 全尺寸图片幻灯片

图 8 三种炸药的POP关系图

Figure 8. Pop plots for the three explosives

下载: 全尺寸图片幻灯片

表 1 实验炸药配方及平均密度

Table 1. Formula and average density of the samples

编号	炸药配方(质量比)	平均密度/(g·cm^-3)
1	CL-20 (95%CL-20, 5%Binder)	1.94
2	CL-20/NTO (47%CL-20, 47%NTO, 6%FPM)	1.89
3	CL-20/FOX-7 (47%CL-20, 47%FOX-7, 6%FPM)	1.88

下载: 导出CSV

表 2 8701和TNT的材料参数^[7]

Table 2. Parameters of TNT and 8701 explosive

炸药	ρ/(g·cm^-3)	D/(cm·μs^-1)	P_CJ/GPa	A/GPa	B/GPa	R₁	R₂	ω	E₀/GPa
8701	1.70	0.831 5	29.50	854.5	20.49	4.60	1.35	0.25	8.5
TNT	1.64	0.693 0	27.00	371.3	3.23	4.15	0.95	0.30	7.0

下载: 导出CSV

表 3 几种惰性材料的Grüneisen状态方程参数^[7]

Table 3. Grüneisen parameters for inert materials

惰性材料	ρ₀/(g·cm^-3)	c/(mm·μs^-1)	S₁	S₂	S₃	γ₀	a
PMMA	1.851	2.240	2.090	-1.12	0.0	0.850	0.00
Steel	7.830	4.570	1.490	0.00	0.0	1.930	0.50
Al	2.700	5.355	1.345	0.00	0.0	2.130	0.48
Polyimide	1.414	2.470	1.629	0.00	0.0	1.395	0.00

下载: 导出CSV

表 4 CL-20、CL-20/NTO、CL-20/FOX-7混合炸药的点火增长模型参数

Table 4. Ignition and growth model parameters for CL-20, CL-20/NTO and CL-20/FOX-7

参数	未反应JWL状态方程
参数	CL-20	CL-20/NTO	CL-20/FOX-7
ρ₀/(g·cm^-3)	1.94	1.89	1.88
A/GPa	444 400	24 900	122 300
B/GPa	-5.13	-3.18	-6.91
R₁	13.5	11.3	11.3
R₂	1.35	1.13	1.13
ω	0.869 5	0.869 5	0.869 5
Cv/(GPa·K^-1)	2.78×10^-3	2.78×10^-3	2.78×10^-3
T₀/K	298	298	298
剪切模量/GPa	4.54	4.00	4.00
屈服强度/GPa	0.2	0.2	0.2

参数	爆轰产物JWL状态方程
参数	CL-20	CL-20/NTO	CL-20/FOX-7
A/GPa	1 887.64	1 640.27	1 589.47
B/GPa	162.40	22.26	18.34
R₁	6.50	5.93	5.78
R₂	2.75	1.76	1.54
ω	0.547	0.700	0.700
Cv/(GPa·K^-1)	1.0×10^-3	1.0×10^-3	1.0×10^-3
E₀/GPa	11.50	8.46	9.07

参数	点火增长反应速率方程
参数	CL-20	CL-20/NTO	CL-20/FOX-7
I	7.43×10¹¹	4.0×10⁶	7.43×10¹¹
a	0.0	0.22	0.0
b	0.667	0.667	0.667
x	20.0	7.0	20.0
G₁	402	402	254
c	0.667	0.667	0.667
d	0.333	0.333	0.333
y	2.0	2.0	2.0
G₂	400	0.6	140
e	0.333	0.667	0.667
g	1.0	0.111	0.333
z	2.0	1.0	2.0
F_igmax	0.3	0.3	0.3
F_G1max	0.5	0.5	0.5
F_G2min	0.5	0.0	0.0

下载: 导出CSV

表 5 CL-20/NTO和CL-20/FOX-7两种混合炸药的配方和生成热数据

Table 5. Formula and heat of formation for the explosive of CL-20/NTO and CL-20/FOX-7

炸药配方(质量比)	生成热/(J·g^-1)	物质的量(分子量为100时)/mol
炸药配方(质量比)	生成热/(J·g^-1)	C	H	N	O	F
CL-20:NTO:FPM(47:47:6)	-189.86	1.537 5	1.507 4	2.733 9	2.372 3	0.200 7
CL-20:FOX-7:FPM(47:47:6)	-141.53	1.449 5	2.054 6	2.558 0	2.558 0	0.200 7

下载: 导出CSV

表 6 三种混合炸药冲击起爆的临界阈值

Table 6. Shock initiation critical thresholds for three mixed explosives

炸药(质量比)	密度/(g·cm^-3)	临界压力/GPa	p²τ/(Pa²·s)	puτ/(J·m^-2)
CL-20(95/5)	1.94	1.39	253.67×10¹⁰	41.97×10⁴
CL-20/NTO/FPM(47/47/6)	1.89	1.46	279.86×10¹⁰	66.71×10⁴
CL-20/FOX-7/FPM(47/47/6)	1.88	1.40	257.33×10¹⁰	43.19×10⁴

下载: 导出CSV

参考文献(14)

[1]	Nielsen A T, Nissan R A.Polynitropolyaza caged explosives[J].Naval Weapon Center Technical Publication, 1986(5):6692.
[2]	Simpson R L, Urtiew P A, Ornellas D L, et al.CL-20 performance exceeds that of HMX and its sensitivity is moderate[J].Propellants, Explosive, Pyrotechnics, 1997, 22(5):249-255. doi: 10.1002/(ISSN)1521-4087
[3]	Tarver C M, Simposon R L, Urtiew P A. Shock initiation of an ε-CL-20-estane formulation[C]//Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Metter. AIP Publishing LLC, 1996: 891-894.
[4]	Lee E L, Tarver C M. Phenomenological model of shock initiation in heterogeneous explosives[C]//Physics of Fluids. AIP Conference Proceedings. AIP Publishing LLC, 1980: 2262-2372.
[5]	Hallquist J O.LS-DYNA user's manual:nonlinear dynamic analysis of structures in three dimensions[M].California:University of California, 2001:823-826.
[6]	Lee E, Finger M, Collins W. JWL equation of state coefficients for high explosives: UCLD-16189[R], 1973.
[7]	陈朗, 刘群, 伍俊英.受热炸药的冲击起爆特征[J].爆炸与冲击, 2013, 33(1):21-28. doi: 10.3969/j.issn.1001-1455.2013.01.003 Chen Lang, Liu Qun, Wu Junying.On shock initiation of heated explosives[J].Explosion and Shock Waves, 2013, 33(1):21-28. doi: 10.3969/j.issn.1001-1455.2013.01.003
[8]	Daniel J S. An equation of state for ploy-methyl-meth acrylate: UCID-16982[R], 1975.
[9]	Mader C L.Numerical modeling of detonation[M].Berkeley:California Press, 1979.
[10]	Mader C L. Detonation properties of condensed explosives computed using the BKW equation of state: LA-2900[R]. Los Alamos Scientific Laboratory Report, 1963.
[11]	Tarver C M, Hallquist J O, Erickson L M. Modeling short pulse duration shock initiation of solid explosives[C]//Proceedings of the 8th International Symposium of Detonation. Albuquerque, USA, 1985: 951-961.
[12]	Urtiew P A, Vandersall K S, Tarver C M, et al.Shock initiation of composition B and C-4 explosives:experiments and modeling[J].Russian Journal of Physical Chemistry:B, 2008, 2:162-171. doi: 10.1134/S1990793108020036
[13]	Walker F E, Wasley R J.Critical energy for shock initiation of heterogeneous explosives[J].Explosives Stoffe, 1969, 17(1):9-13. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000001148783
[14]	Ramsay J B, Popolato A. Analysis of shock wave and initiation data for solid explosives: LA-DC-6992;CONF-651003-3[R]. Los Alamos Scientific Lab., Univ. of California, N. Mex., 1965.