Velocity distribution of fragments resulted by explosion of a cylindrical shell charge on multi-spots eccentric initiation
-
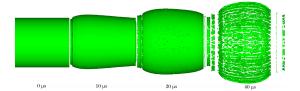
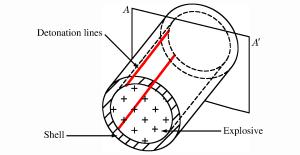
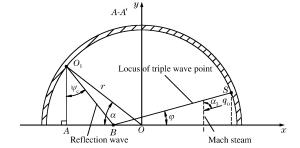
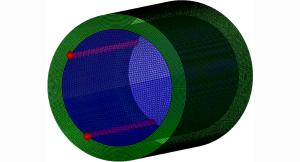
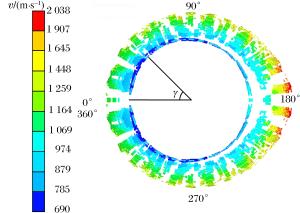
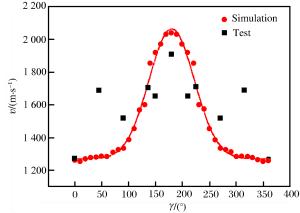
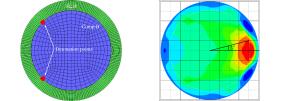
摘要: 针对偏心起爆战斗部破片速度增益的问题，提出爆轰波碰撞形成马赫超压是引起破片速度增加的原因。利用AUTODYN软件，模拟偏心起爆战斗部从壳体径向膨胀、表面产生裂纹到最后形成破片的整个过程，并将模拟得到的破片速度与实验数据对比，两者吻合较好；简化Whitham方法并结合Gurney速度公式得到偏心起爆战斗部定向破片速度和定向区域的计算方法，同时在保证破片初速的前提下，研究偏心多点起爆下起爆点数的选择标准。研究结果表明：偏心多点起爆下定向破片初速增益约34%，定向区域范围约30°，起爆点数的选择与壳体长度和装药口径相关。Abstract: To address the issue of the increase of the fragment velocity of an eccentric initiation warhead, we put forward the view that this increase was caused by the Mach overpressure formed by the detonation wave collision. We used the AUTODYN software to simulate the whole explosion process of the eccentric initiation warhead, from the radial expansion of the shell to the formation of the surface cracks, and eventually the formation of the fragments. We then compared the simulation result of the fragment velocity with the test data and found that they were in good agreement. Further we combined the simplified Whitham method with the Gurney equation to obtain the calculation method of the directional fragment velocity and directional area of the eccentric initiation warhead. We studied the selection criteria for the number of the initiation spot on the premise of maintaining the fragment velocity. The results show that through the multi-spot eccentric initiation, the velocity of the directional fragment increases by about 34%, and the directional area range is approximately 30°; the selection criteria of the number of initiation spot is associated with the shell length and the charge diameter. Our study can provide a reference for the engineering application of multi-spot initiation eccentric warhead.
-
图 2 中心单点端面起爆破片形成示意图
Figure 2. Process of the fragment formation under center detonation with single point
图 3 不同位置处破片初速的变化
Figure 3. Variation of initial velocity of fragments at different positions
图 10 不同起爆点数下破片速度比较
Figure 10. Comparison of fragment initial velocities under different number of detonation points
图 11 破片最大速度随爆点点数的变化
Figure 11. Variation of fragment maximum velocity with detonation point number
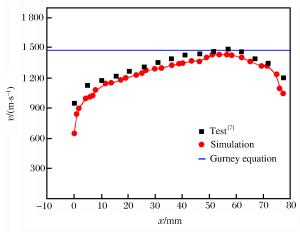
表 1 实验数据与理论模型结果对比
Table 1. Comparison between experimental and theoretical data
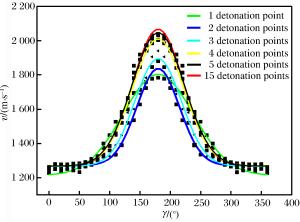
编号 v/(m·s-1) 编号 v/(m·s-1) 编号 v/(m·s-1) 编号 v/(m·s-1) 实验 数值模拟 实验 数值模拟 数值模拟 数值模拟 1 954 650 9 1 432 1 150 17 1 329 25 1 436 2 1 129 845 10 1 445 1 183 18 1 340 26 1 430 3 1 182 901 11 1 469 1 198 19 1 349 27 1 410 4 1 222 1 000 12 1 493 1 232 20 1 372 28 1 363 5 1 270 1 013 13 1 463 1 249 21 1 365 29 1 323 6 1 309 1 032 14 1 398 1 274 22 1 405 30 1 326 7 1 354 1 079 15 1 347 1 290 23 1 430 31 1 240 8 1 396 1 145 16 1 208 1 298 24 1 436 32 1 095 
下载: 导出CSV
-
[1] 王树山, 马晓飞, 隋树元, 等.偏心多点起爆战斗部破片飞散实验研究[J].北京理工大学学报, 2001, 21(2):177-179. doi: 10.3969/j.issn.1001-0645.2001.02.008Wang Shushan, Ma Xiaofei, Sui Shuyuan, et al. Experimental research on fragments dispersion of the warhead under asymmetrical multi-spots initiation[J]. Journal of Beijing Institute of Technology, 2001, 21(2):177-179. doi: 10.3969/j.issn.1001-0645.2001.02.008 [2] 黄静, 孔凡勋, 袁晋等.多点偏心起爆对破片速度增益的影响[J].现代防御技术, 2011, 39(6):37-42. doi: 10.3969/j.issn.1009-086x.2011.06.008Huang Jing, Kong Fanxun, Yuan Jin, et al. Influence of multi-spots off-axis initiation on fragment velocity gain[J]. Modern Defence Technology, 2011, 39(6):37-42. doi: 10.3969/j.issn.1009-086x.2011.06.008 [3] 张博, 李伟兵, 李文彬, 等.偏心起爆战斗部随机破片数值仿真[J].高压物理学报, 2012, 26(4):442-448. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201204330132Zhang Bo, Li Weibing, Li Wenbin, et al. Numerical simulation of the dispersion of random fragments under asymmetrical initiation[J]. Chinese Journal of High Pressure Physics, 2012, 26(4):442-448. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201204330132 [4] Century Dynamics Inc. AUTODYN theory manual revision 4.2[M]. San Ramon: Century Dynamics Inc, 2001. [5] 糜仲春.马赫反射研究进展[J].力学进展, 1982, 12(1):41-50. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000004351791Mi Zhongchun. Recent advances in mach reflection[J]. Advances in mechanics, 1982, 12(1):41-50. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000004351791 [6] 黄正祥, 祖旭东.终点效应[M].北京:科学出版社, 2014:83-102. [7] Huang G Y, Li W, Feng S S. Axial distribution of fragment velocities from cylindrical casing under explosive loading[J]. International Journal of Impact Engineering, 2015, 76(2):20-27. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=5711d4fa928e6154bef591da048e4f4b [8] 耿荻, 马天宝, 宁建国.定向战斗部爆炸驱动规律研究[J].爆炸与冲击, 2013, 27(5):685-690. http://www.gywlxb.cn/CN/Y2013/V27/I5/685Geng Di, Ma Tianbao, Ning Jianguo. Study on laws of explosive driven behaviors of aimed warhead[J]. Chinese Journal of High Pressure Physics, 2013, 27(5):685-690. http://www.gywlxb.cn/CN/Y2013/V27/I5/685 [9] 王继海.二维非定常流和激波[M].北京:科学出版社, 1994:82-100. -
点击查看大图
计量
- 文章访问数: 4296
- HTML全文浏览量: 1430
- PDF下载量: 435
- 被引次数: 0