液态燃料对连续旋转爆轰发动机爆轰特性的影响

李宝星; 翁春生

doi:10.11883/bzycj-2016-0240

液态燃料对连续旋转爆轰发动机爆轰特性的影响

doi: 10.11883/bzycj-2016-0240

李宝星,
翁春生^,

南京理工大学瞬态物理国家重点实验室，江苏南京 210094

基金项目:

国家自然科学基金项目 11702143

国家自然科学基金项目 11472138

中央高校基本科研业务费专项基金项目 30920140112011

江苏省研究生科研与实践创新计划项目 KYCX17_0357

详细信息

作者简介:
李宝星(1990-)，男，博士研究生

通讯作者:
翁春生，wengcs@126.com

中图分类号: O381
计量
- 文章访问数: 5243
- HTML全文浏览量: 2207
- PDF下载量: 238
- 被引次数: 0
出版历程
- 收稿日期: 2016-08-16
- 修回日期: 2016-12-12
- 刊出日期: 2018-03-25

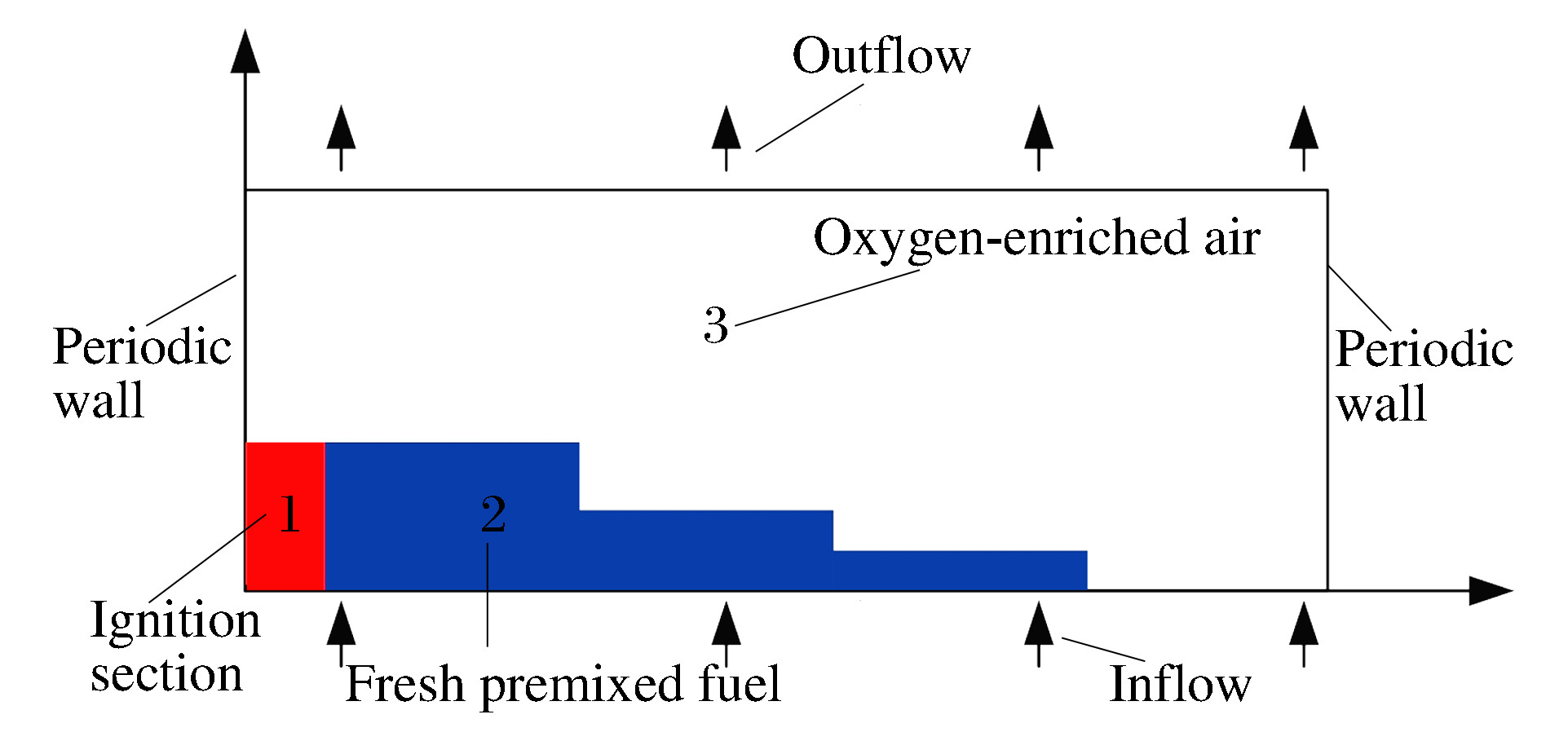
Influence of liquid fuel on the detonation characteristics of continuous rotating detonation engine

LI Baoxing,
WENG Chunsheng^,

National Key Lab of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

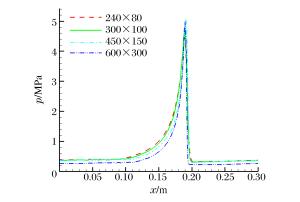
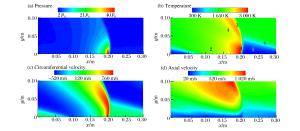
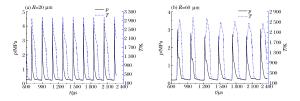
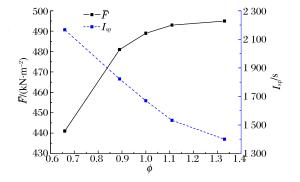
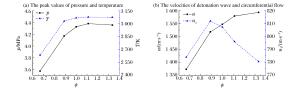
摘要: 为了研究液态燃料对连续旋转爆轰发动机爆轰特性的影响，采用CE/SE方法对以汽油/富氧空气为燃料的CRDE进行数值模拟，分析了不同液滴半径、当量比对爆轰性能参数的影响。计算结果表明：随着液滴半径增大，爆轰压力峰值、温度峰值以及爆轰波速度均降低，且压力峰值与温度峰值在爆轰波传播过程中出现不稳定现象；当增大到70 μm时，爆轰波将无法成功起爆。随着当量比的增大，CRDE爆轰波速度及平均推力增大，爆轰压力、温度以及气相周向速度的峰值均先增大后减小。在当量比1.1附近，爆轰压力与温度的峰值出现极大值；而气相周向速度峰值的极大值出现在当量比0.9附近。基于燃料的比冲随着当量比增大而减小。
- 填充条件 /
- 连续旋转爆轰发动机 /
- CE/SE方法 /
- 比冲
Abstract: In this paper, based on two-dimensional conservation element and solution element(CE/SE), we simulated the detonation process of CRDE with gasoline and oxygen-enriched air to study the influence of liquid fuel on the detonation characteristics of the continuous rotating detonation engine. The effects of different droplet radiuses and equivalence ratios on the detonation parameters were analyzed. Our calculation results show that the velocity of the detonation wave and the peak values of the detonation pressure and temperature decreased with the increase of the droplet radius, and the peak values of the pressure and temperature became unstable during the propagation of the detonation wave. However, the detonation wave were not initiated successfully when the radius rose to 70 μm. The velocity of the detonation wave and the average thrust of CRDE increased with the rising of the equivalence ratio, while the peak values of the detonation pressure, temperature and gas phase's circumferential velocity increased first and then decreased. The peak values of the detonation pressure and temperature reached the maximum when the equivalence ratio was about 1.1, while the maximum of the gas phase's circumferential velocity occurred when the equivalence ratio was about 0.9.The fuel-based specific impulse decreased at the increase of the equivalence ratio.
- filling conditions /
- continuous rotating detonation engine /
- CE/SE /
- specific impulse

HTML全文

图 1 CRDE燃烧室流场计算模型

Figure 1. Calculation model of the flow field of CRDE combustor

下载: 全尺寸图片幻灯片

图 2 压力分布曲线

Figure 2. Distribution of pressure

下载: 全尺寸图片幻灯片

图 3 燃烧室内流场分布情况(t=1 276 μs)

Figure 3. Distribution of flow field in combustor (t=1 276 μs)

下载: 全尺寸图片幻灯片

图 4 燃烧室入口处流场分布(t=1 276 μs)

Figure 4. Distribution of flow field of combustor inlet (t=1 276 μs)

下载: 全尺寸图片幻灯片

图 5 液滴半径随时间变化曲线

Figure 5. Variation curve of droplet radius with time

下载: 全尺寸图片幻灯片

图 6 压力和温度随时间变化曲线(x=0.2 m, y=0 m)

Figure 6. Variation curves of pressure and temperature with time (x=0.2 m, y=0 m)

下载: 全尺寸图片幻灯片

图 8 不同当量比条件下的平均推力和基于燃料的比冲变化情况

Figure 8. Variation curves of average thrust and specific impulse

下载: 全尺寸图片幻灯片

图 7 爆轰参数随当量比变化曲线

Figure 7. Variation curve of detonation parameters with equivalence ratio

下载: 全尺寸图片幻灯片

表 1 不同液滴半径条件下爆轰情况

Table 1. Parameters of detonation at different droplet radius

液滴半径/μm	爆轰压力峰值/MPa	爆轰温度峰值/K	爆轰波速度/(m·s^-1)
20	4.20	3 050	1 568
30	4.11	2 957	1 466
40	3.65	2 743	1 370
50	3.35	2 608	1 265
60	2.78	2 553	1 165
70	-	-	-

下载: 导出CSV

参考文献(21)

[1]	KAILASANATH K. Review of propulsion applications of detonation waves[J]. AIAA journal, 2000, 38(9):1698-1708. doi: 10.2514/2.1156
[2]	王健平, 周蕊, 武丹.连续旋转爆轰发动机的研究进展[J].实验流体力学, 2015, 29(4):12-25. http://www.cnki.com.cn/Article/CJFDTOTAL-LTLC201504002.htm WANG Jianping, ZHOU Rui, WU Dan. Progress of continuously rotating detonation engine research[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(4):12-25. http://www.cnki.com.cn/Article/CJFDTOTAL-LTLC201504002.htm
[3]	BYKOVSKII F A, ZHDAN S A, ADERNIKOV E F. Continuous spin detonation[J]. Journal of Propulsion and Power, 2006, 22(6):1204-1216. doi: 10.2514/1.17656
[4]	BYKOVSKII F A, ZHDAN S A, ADERNIKOV E F. Continuous spin detonation of fuel-air mixtures[J]. Combustion, Explosion, and Shock Waves, 2006, 42(4):463-471. doi: 10.1007/s10573-006-0076-9
[5]	ZHDAN S A, SYRYAMIN A S. Numerical modeling of continuous detonation in non-stoichiometric hydrogen-oxygen mixtures[J]. Combustion, Explosion, and Shock Waves, 2013, 49(1):69-78. doi: 10.1134/S0010508213010085
[6]	SCHWER D, KAILASANATH K. Numerical investigation of the physics of rotating detonation engines[J]. Proceedings of the Combustion Institute, 2011, 33(2):2195-2202. doi: 10.1016/j.proci.2010.07.050
[7]	KINDRACKI J. Experimental research on rotating detonation in liquid fuel-gaseous air mixtures[J]. Aerospace Science and Technology, 2015, 43:445-453. doi: 10.1016/j.ast.2015.04.006
[8]	DAVIDENKO D M, GOKALP I, KUDRYAVTSEV A N. Numerical study of the continuous detonation wave rocket engine: AIAA 2008-2680[R]. 2008.
[9]	TSUBOI N, WATANABE Y, KOJIMA T, et al. Numerical estimation of the thrust performance on a rotating detonation engine for a hydrogen-oxygen mixture[J]. Proceedings of the Combustion Institute, 2014, 35(2):2005-2013. https://www.sciencedirect.com/science/article/pii/S1540748914004313
[10]	WANG Y H, WANG J P. Effect of equivalence ratio on the velocity of rotating detonation[J]. International Journal of Hydrogen Energy, 2015, 40(25):7949-7955. doi: 10.1016/j.ijhydene.2015.04.072
[11]	刘世杰, 刘卫东, 林志勇, 等. 连续旋转爆震波传播过程实验研究[C]//第十五届全国激波与激波管学术会议论文集, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=7714633
[12]	王超, 刘卫东, 刘世杰, 等.连续旋转爆震波传播模态试验[J].国防科技大学学报, 2015, 37(4):121-127. doi: 10.11887/j.cn.201504021 WANG Chao, LIU Weidong, LIU Shijie, et al. Experiment on the propagation mode of continuous rotating detonation wave[J]. Journal of National University of Defense Technology, 2015, 37(4):121-127. doi: 10.11887/j.cn.201504021
[13]	郑权, 翁春生, 白桥栋.当量比对液体燃料旋转爆轰发动机爆轰影响实验研究[J].推进技术, 2015, 36(6):947-952. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tjjs201506020 ZHENG Quan, WENG Chunsheng, BAI Qiaodong. Experimental study on effects of equivalence ratio on detonation characteristics of liquid-fueled rotating detonation engine[J]. Journal of Propulsion Technology, 2015, 36(6):947-952. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tjjs201506020
[14]	武丹, 刘岩, 王健平.连续旋转爆轰发动机参数特性的三维数值模拟[J].航空动力学报, 2015, 30(7):1576-1582. http://www.cnki.com.cn/Article/CJFDTotal-HKDI201507008.htm WU Dan, LIU Yan, WANG Jianping. Three-dimensional numerical simulation of the parametric properties of continuously rotating detonation engine[J]. Journal of Aerospace Power, 2015, 30(7):1576-1582. http://www.cnki.com.cn/Article/CJFDTotal-HKDI201507008.htm
[15]	归明月, 范宝春, 张旭东, 等.旋转爆轰的三维数值模拟[J].推进技术, 2010, 31(1):82-86. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201407003026.htm GUI Mingyue, FAN Baochun, ZHANG Xudong, et al. Three-dimensional simulation of continuous spin detonation engine[J]. Journal of Propulsion Technology, 2010, 31(1):82-86. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201407003026.htm
[16]	李宝星, 翁春生.连续旋转爆轰发动机气液两相爆轰波传播特性二维数值研究[J].固体火箭技术, 2015, 38(5):646-652. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gthjjs201505008 LI Baoxing, WENG Chunsheng. Numerical investigation on two-dimensional gas-liquid two-phase detonation wave propagation characteristics of continuous rotating detonation engine[J]. Journal of Solid Rocket Technology, 2015, 38(5):646-652. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gthjjs201505008
[17]	翁春生, 王浩.计算内弹道学[M].北京:国防工业出版社, 2006.
[18]	马丹花, 翁春生.二维守恒元和求解元方法在两相爆轰流场计算中的应用[J].燃烧科学与技术, 2010, 16(1):85-91. http://d.old.wanfangdata.com.cn/Periodical/rskxyjs201001016 MA Danhua, WENG Chunsheng. Application of two-dimensional CE/SE method to calculation of two-phase detonation Flow Field[J]. Journal of Combustion Science and Technology, 2010, 16(1):85-91. http://d.old.wanfangdata.com.cn/Periodical/rskxyjs201001016
[19]	洪滔, 秦承森.气体-燃料液滴两相系统爆轰的数值模拟[J].爆炸与冲击, 1999, 19(4):335-342. http://www.bzycj.cn/CN/abstract/abstract10364.shtml HONG Tao, QIN Chengsen. Numerical simulation of detonation of gas-fuel droplet two-phase system[J]. Explosion and Shock Waves, 1999, 19(4):335-342. http://www.bzycj.cn/CN/abstract/abstract10364.shtml
[20]	彭振, 翁春生.脉冲爆轰发动机中等离子体点火的数值计算[J].工程力学, 2012, 29(5):242-250. http://d.old.wanfangdata.com.cn/Conference/7761871 PENG Zhen, WENG Chunsheng. Numerical calculation of plasma ignition on pulse detonation engine[J]. Engineering Mechanics, 2012, 29(5):242-250. http://d.old.wanfangdata.com.cn/Conference/7761871
[21]	王治武, 严传俊, 李牧, 等.燃油粒度对两相PDE爆震波速的影响[J].工程热物理学报, 2006, 27(6):1057-1059. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcrwlxb200606050 WANG Zhiwu, YAN Chuanjun, LI Mu, et al. Droplet size effect on detonation velocity of two-phase pulse detonation engine[J]. Journal of Engineering Thermophysics, 2006, 27(6):1057-1059. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcrwlxb200606050