Dynamic shear behavior and failure mechanism of Ti-6Al-4V at high strain rates
-
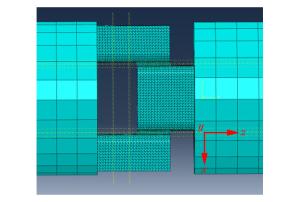
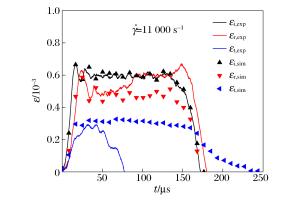
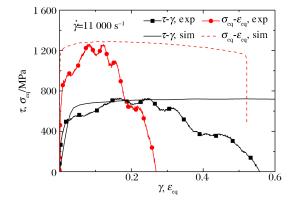
摘要: 采用基于霍普金森压杆的新型加载技术对Ti-6Al-4V材料的动态剪切特性及失效机理进行了测试研究。获得了Ti-6Al-4V材料在超过104 s-1应变率下的剪应力-剪应变曲线及失效参数。研究发现,材料的流动应力存在明显的应变率强化效应;随着应变率的增加,材料的失效应力逐渐增大,而失效应变逐渐减小。采用ABAQUS/Explicit对加载过程进行了数值模拟。结果显示,剪切区材料基本处于平面剪切状态,应力应变场分布较为均匀,计算得到的剪应力-剪应变曲线与实验结果吻合较好。经断口分析可知,随着应变率的升高,Ti-6Al-4V的失效机理存在由韧窝、拉伸韧窝至台阶及河流花样的演化过程,材料的失效模式主要表现为韧性断裂。Abstract: Dynamic shear properties and failure mechanism of Ti-6Al-4V were studied at strain rates in excess of 104 s-1, with a new loading method based on the split Hopkinson pressure bar (SHPB) technique. The shear stress-shear strain curves and failure parameters of Ti-6Al-4V were acquired in a wide range of high shear strain rates. It is found that the flow stress of the material shows an obvious strain rate hardening effect. With the increase of strain rates, the failure stress of the material increases gradually, while the failure strain decreases. The loading process was modeled by ABAQUS/Explicit software. The results show that the shear zone material is substantially in the state of plane shear. The tested stress-strain curves have good agreement with the simulated results. The fracture surface examination shows that with the increase of strain rate, the failure of Ti-6Al-4V is closely related to the different behaviors of dimples, and it indicates an evolution process from dimples and tensile dimples to steps and river patterns. The fracture analyses show that the failure mode of the material is mainly ductile fracture.
-
Key words:
- dynamic shear /
- double shear specimen /
- high strain rate /
- micro-mechanism
-
表 1 数值模拟的主要材料参数
Table 1. Material parameters in FE simulation
部位 材料 ρ/(g·cm-3) E/GPa ν λ/(W·m-1·K-1) 入射杆 18Ni钢 8.0 190 0.3 - 试样 Ti-6Al-4V 4.43 114 0.33 6.7 透射杆 7075铝合金 2.7 70 0.3 - -
[1] BAI Y, DODD B. Adiabatic shear localization: Occurrence, theories and applications[J]. Oxford University Press, 1992. [2] LIAO S C, DUFFY J. Adiabatic shear bands in a Ti-6Al-4V titanium alloy[J]. Journal of the Mechanics and Physics of Solids, 1998, 46(11):2201-2231. doi: 10.1016/S0022-5096(98)00044-1 [3] RITTEL D, WANG Z G. Thermo-mechanical aspects of adiabatic shear failure of AM50 and Ti-6Al-4V alloys[J]. Mechanics of Materials, 2008, 40(8):629-635. doi: 10.1016/j.mechmat.2008.03.002 [4] PEIRS J, VERLEYSEN P, DEGRIECK J, et al. The use of hat-shaped specimens to study the high strain rate shear behaviour of Ti-6Al-4V[J]. International Journal of Impact Engineering, 2010, 37(6):703-714. doi: 10.1016/j.ijimpeng.2009.08.002 [5] CHICHILI D R, RAMESH K T, HEMKER K J. Adiabatic shear localization in α-titanium:Experiments, modeling and microstructural evolution[J]. Journal of the Mechanics and Physics of Solids, 2004, 52(8):1889-1909. doi: 10.1016/j.jmps.2004.02.013 [6] RITTEL D, LEE S, RAVICHANDRAN G. A shear-compression specimen for large strain testing[J]. Experimental Mechanics, 2002, 42(1):58-64. doi: 10.1007/BF02411052 [7] DOROGOY A, RITTEL D, GODINGER A. A shear-tension specimen for large strain testing[J]. Experimental Mechanics, 2016, 56(3):437-449. doi: 10.1007/s11340-015-0106-1 [8] 林艺生, 傅学金, 杨月诚.30CrMnSiA绝热剪切带显微观察与分析[J].兵器材料科学与工程, 2010, 33(6):59-61. doi: 10.3969/j.issn.1004-244X.2010.06.018LIN Yisheng, FU Xuejin, YANG Yuecheng. Microstructure observation and analysis of adiabatic shear band in 30CrMnSiA steel[J]. Ordnance Material Science and Engineering, 2010, 33(6):59-61. doi: 10.3969/j.issn.1004-244X.2010.06.018 [9] MEYERS M A, CHEN Y J, MARQUIS F D S, et al. High-strain, high-strain-rate behavior of tantalum[J]. Metallurgical and Materials Transactions:A, 1995, 26(10):2493-2501. doi: 10.1007/BF02669407 [10] 魏志刚, 李永池, 李剑荣, 等.冲击载荷作用下钨合金材料绝热剪切带形成机理[J].金属学报, 2000, 36(12):1263-1268. doi: 10.3321/j.issn:0412-1961.2000.12.008WEI Zhigang, LI Yongchi, LI Jianrong, et al. Formation mechanism of adiabatic shear band in tungsten heavy alloys[J]. Acta Metallurgica Sinica, 2000, 36(12):1263-1268. doi: 10.3321/j.issn:0412-1961.2000.12.008 [11] ROGERS H C, SHASTRY C V. Shock waves and high-strain-rate phenomena in metals[M]. Plenum Press, 1981:683. [12] FERGUSON W G, HAUSER F E, DORN J E. Dislocation damping in zinc single crystals[J]. British Journal of Applied Physics, 1967, 18(18):411-417. http://adsabs.harvard.edu/abs/1967BJAP...18..411F [13] 刘新芹, 谭成文, 张静, 等.应力状态对Ti-6Al-4V绝热剪切敏感性的影响[J].稀有金属材料与工程, 2008, 37(9):1522-1525. doi: 10.3321/j.issn:1002-185X.2008.09.004LIU Xinqin, TAN Chengwen, ZHANG Jing, et al. Influence of stress-state on adiabatic shear sensitivity of Ti-6Al-4V[J]. Rare Metal Materials and Engineering, 2008, 37(9):1522-1525. doi: 10.3321/j.issn:1002-185X.2008.09.004 [14] ZHANG Jing, TAN Chengwen, REN Yu, et al. Adiabatic shear fracture in Ti-6Al-4V alloy[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(11):2396-2401. doi: 10.1016/S1003-6326(11)61026-1 [15] 苏冠龙, 龚煦, 李玉龙, 等.TC4在动态载荷下的剪切行为研究[J].爆炸与冲击, 2015, 35(4):527-535. http://www.bzycj.cn/CN/abstract/abstract9496.shtmlSU Guanlong, GONG Xu, LI Yulong, et al. Shear behavior of TC4 alloy under dynamic loading[J]. Explosion and Shock Waves, 2015, 35(4):527-535. http://www.bzycj.cn/CN/abstract/abstract9496.shtml [16] LANDAU P, VENKERT A, RITTEL D. Microstructural aspects of adiabatic shear failure in annealed Ti6AL4V[J]. Metallurgical and Materials Transactions:A, 2010, 41(2):389-396. doi: 10.1007/s11661-009-0098-5 [17] GUO Yazhou, LI Yulong. A novel approach to testing the dynamic shear response of Ti-6Al-4V[J]. Acta Mechanica Solida Sinica, 2012, 25(3):299-311. doi: 10.1016/S0894-9166(12)60027-5 [18] LONGÈRE P, DRAGON A. Dynamic vs. quasi-static shear failure of high strength metallic alloys:Experimental issues[J]. Mechanics of Materials, 2015, 80:203-218. doi: 10.1016/j.mechmat.2014.05.001 [19] 许泽建, 丁晓燕, 张炜琪, 等.一种用于材料高应变率剪切性能测试的新型加载技术[J].力学学报, 2016, 48(3):654-659. http://d.old.wanfangdata.com.cn/Periodical/lxxb201603015XU Zejian, DING Xiaoyan, ZHANG Weiqi, et al. A new loading technique for measuring shearing properties of materials under high strain rates[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3):654-659. http://d.old.wanfangdata.com.cn/Periodical/lxxb201603015 [20] XU Zejian, DING Xiaoyan, ZHANG Weiqi, et al. A novel method in dynamic shear testing of bulk materials using the traditional SHPB technique[J]. International Journal of Impact Engineering, 2017, 101:90-104. doi: 10.1016/j.ijimpeng.2016.11.012 [21] NEMAT-NASSER S. Hopkinson techniques for dynamic recovery experiments[J]. Proceedings of the Royal Society:A, 1991, 435:371-391. doi: 10.1098/rspa.1991.0150 [22] SEO S, MIN O, YANG H. Constitutive equation for Ti-6Al-4V at high temperatures measured using the SHPB technique[J]. International Journal of Impact Engineering, 2005, 31(6):735-754. doi: 10.1016/j.ijimpeng.2004.04.010 [23] 钟群鹏, 赵子华.断口学[M].北京:高等教育出版社, 2006. -






 下载:
下载: