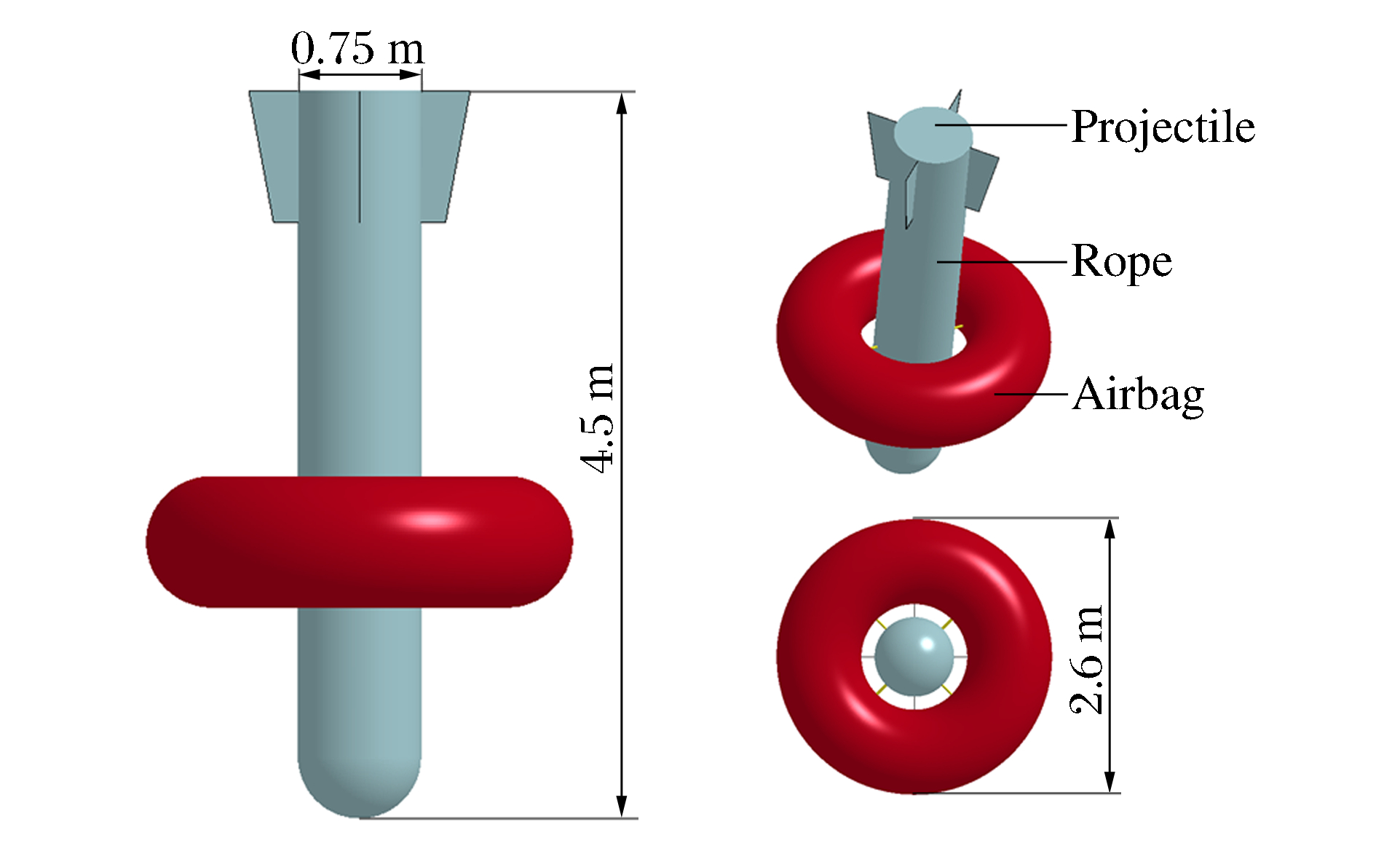
Numerical analysis of the water entry process of a projectile with a circular airbag
-
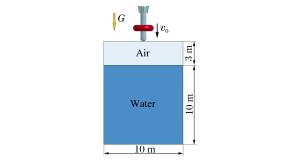
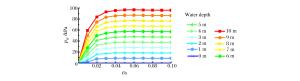
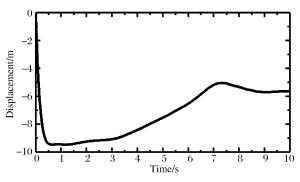
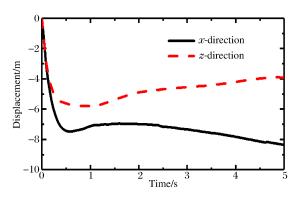
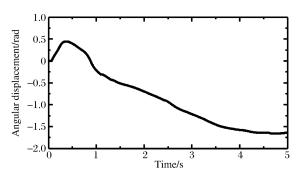
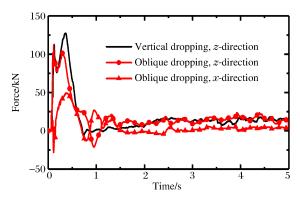
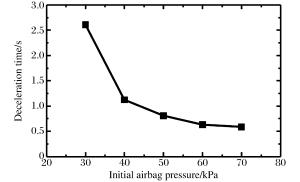
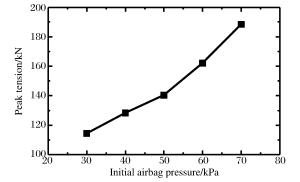
摘要: 针对带环形密闭气囊弹体入水冲击问题,基于LS-DYNA,运用控制体积法模拟环形密闭气囊,结合流固耦合算法,模拟了某弹体及附带环形密闭气囊入水过程。将入水过程分为弹体砰水、气囊着水、入水减速、水中悬停、缓慢上浮、上浮出水、水面漂浮7个主要阶段,对比分析了垂直与倾斜入水过程中不同阶段弹体和气囊的姿态变化、减速特性及入水深度等特征的异同。从气囊内压变化、流体对气囊的作用合力、气囊内压与入水速度的关系等方面研究了流体与气囊的相互作用,发现入水过程中气囊内压的变化主要受入水深度、运动速度、连接绳拉力等因素影响。通过计算不同初始内压条件下弹体的入水深度、减速时间及连接绳的拉力峰值,发现囊压越高,入水深度越小,减速时间越短,但是相应连接绳对弹体外壳的拉力峰值越大。因此,在进行入水回收气囊参数设计时,需要综合考虑缓冲效果、减速效果及气囊安全性等因素。Abstract: Using the control volume method to describe annular an airtight airbag, we simulated the water entry process of a projectile and its annular airtight airbag based on LS-DYNA combined with the fluid-solid coupling algorithm. We divided this process into seven stages, i.e. those of the projectile slamming water, its air bag falling into water, decelerating in water-entry, hovering in water, floating upward in water, floating out of water, floating on the water surface. We analyzed the projectile's attitude change, deceleration, water entry depth and airbag in different stages in vertical and oblique water-entry. Then we examined the interaction between water and the airbag, covering the changes of the internal pressure, the resultant force of water to the airbag, the relationship between airbag's internal pressure and speed of the water-entry. The results show that the change of the internal pressure of the airbag is mainly affected by the water-entry depth, the movement speed, and the tension of the connecting rope. Further, we calculated the water-entry depth, the deceleration time and the tension peak of the connecting rope under the airbag's different initial internal pressures, and found that the water-entry depth and the deceleration time decrease with the increase of the airbag's initial pressure, while the tension peak of the corresponding connecting rope exhibited an opposite tendency. Therefore, it is necessary to consider the buffering effect, deceleration effect, airbag safety and other factors in the design of airbag parameters.
-
Key words:
- airtight airbag /
- water-entry impact /
- control volume method /
- fluid-solid coupling /
- LS-DYNA
-
表 1 气囊和连接绳的材料参数
Table 1. Material parameters of the airbag and corresponding rope
材料 ρ/(kg·m-3) μ E/GPa 气囊 875 0.2 0.557 连接绳 840 0.2 21.9 表 2 水和空气参数
Table 2. Parameters of water and air
材料 ρ/(kg·m-3) pc/Pa ν/(mPa·s) C/(m·s-1) S1 S2 S3 γ0 水 998 -10 000 870 1 480 2.56 -1.99 0.227 0.5 空气 1.185 -10 0.018 4 340 0 0 0 1.4 -
[1] 陈帅, 李斌, 温金鹏, 等.软着陆气囊缓冲特性与参数设置的理论研究[J].振动与冲击, 2009, 28(4):25-28. doi: 10.3969/j.issn.1000-3835.2009.04.006CHEN Shuai, LI Bin, WEN Jinpeng, et al. Cushioning characteristic and parameter design of a soft landing airbag[J]. Journal of Vibration and Shock, 2009, 28(4):25-28. doi: 10.3969/j.issn.1000-3835.2009.04.006 [2] 温金鹏, 李斌, 谭德伟, 等.考虑织布弹性的软着陆气囊缓冲特性研究[J].振动与冲击, 2010, 29(2):79-83. doi: 10.3969/j.issn.1000-3835.2010.02.018WEN Jinpeng, LI Bin, TAN Dewei, et al. Cushioning characteristics of a soft landing airbag with elastic fabric[J]. Journal of Vibration and Shock, 2010, 29(2):79-83. doi: 10.3969/j.issn.1000-3835.2010.02.018 [3] 卫剑征, 谭惠丰, 万志敏, 等.缓冲气囊展开与缓冲着陆过程的仿真分析[J].航天返回与遥感, 2010, 31(5):1-8. doi: 10.3969/j.issn.1009-8518.2010.05.001WEI Jianzheng, TAN Huifeng, WAN Zhimin, et al. Simulation for airbag deployment and landing process of inflatable landing vechiles[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(5):1-8. doi: 10.3969/j.issn.1009-8518.2010.05.001 [4] 邓春燕, 裴锦华.全向式着陆缓冲气囊的折叠建模与充气过程仿真[J].南京航空航天大学学报, 2009, 41(增刊1):97-102. http://d.old.wanfangdata.com.cn/Periodical/njhkht2009z2022DENG Chunyan, PEI Jinhua. Modeling and process simulating about folding and inflating of omni-directional-type airbag[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(Suppl 1):97-102. http://d.old.wanfangdata.com.cn/Periodical/njhkht2009z2022 [5] 蔡文, 李斌, 温金鹏, 等.无人机软着陆气囊缓冲特性研究[J].兵工学报, 2014, 35(11):1867-1875. doi: 10.3969/j.issn.1000-1093.2014.11.019CAI Wen, LI Bin, WEN Jinpeng, et al. Research on cushioning characteristics of UAV soft landing airbags[J]. Acta Armamentarii, 2014, 35(11):1867-1875. doi: 10.3969/j.issn.1000-1093.2014.11.019 [6] 邵志建, 裴锦华.某无人机横向圆柱排气式气囊着陆装置缓冲过程研究[J].航天返回与遥感, 2016, 37(2):26-33. http://d.old.wanfangdata.com.cn/Periodical/htfhyyg201602004SHAO Zhijian, PEI Jinghua. Simulation of bi-cylindrical airbag cushioning system for pilotless aircraft[J]. Spacecraft Recovery & Remote Sensing, 2008, 20(5):1325-1327. http://d.old.wanfangdata.com.cn/Periodical/htfhyyg201602004 [7] 温金鹏, 李斌, 杨智春.缓冲气囊冲击减缓研究进展[J].宇航学报, 2010, 31(11):2438-2447. doi: 10.3873/j.issn.1000-1328.2010.11.002WEN Jinpeng, LI Bin, YANG Zhichun. Progress of study on impact attenuation capability of airbag cushion system[J]. Journal of Astronautics, 2010, 31(11):2438-2447. doi: 10.3873/j.issn.1000-1328.2010.11.002 [8] 秦洪德, 赵林岳, 申静.入水冲击问题综述[J].哈尔滨工业大学学报, 2011(增刊1):152-157. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201100301355QIN Hongde, ZHAO Linyue, SHEN Jing. Review of water entry problem[J]. Journal of Harbin Institute of Technology, 2011(Suppl 1):152-157. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201100301355 [9] WORTHINGTON A M, COLE R S. Impact with a liquid surface studied with aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society of London, 1900, 194:175-199. doi: 10.1098/rsta.1900.0016 [10] 王永虎, 石秀华.入水冲击问题研究的现状与进展[J].爆炸与冲击, 2008, 28(3):276-282. doi: 10.3321/j.issn:1001-1455.2008.03.014WANG Yonghu, SHI Xiuhua. Review on research and development of water-entry impact problem[J]. Explosion and Shock Waves, 2008, 28(3):276-282. doi: 10.3321/j.issn:1001-1455.2008.03.014 [11] 卢炽华, 何友声.二维弹性结构入水冲击过程中的流固耦合效应[J].力学学报, 2000, 32(2):129-140. doi: 10.3321/j.issn:0459-1879.2000.02.001LU Chihua, HE Yousheng. Coupled analysis of nonlinear interaction between fluid and structure during impact[J]. Acta Mechanica Sinica, 2000, 32(2):129-140. doi: 10.3321/j.issn:0459-1879.2000.02.001 [12] 李飞, 孙凌玉, 张广越, 等.圆柱壳结构入水过程的流固耦合仿真与试验[J].北京航空航天大学学报, 2007, 33(9):1117-1120. doi: 10.3969/j.issn.1001-5965.2007.09.027LI Fei, SUN Lingyu, ZHANG Guangyue, et al. Simulation and experiment of cylinder shell structure dropping into water based on fluid structure interaction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(9):1117-1120. doi: 10.3969/j.issn.1001-5965.2007.09.027 [13] 施红辉, 胡青青, 陈波, 等.钝体倾斜和垂直冲击入水时引起的超空泡流动特性实验研究[J].爆炸与冲击, 2015, 35(5):617-624. http://www.bzycj.cn/CN/abstract/abstract9509.shtmlSHI Honghui, HU Qingqing, CHEN Bo, et al. Experimental study of supercavitating flows induced by oblique and vertical water entry of blunt bodies[J]. Explosion and Shock Waves, 2015, 35(5):617-624. http://www.bzycj.cn/CN/abstract/abstract9509.shtml [14] 程涵.气囊工作过程仿真研究[D].南京: 南京航空航天大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10287-1011253523.htmCHENG Han. Numerical simulation research on airbag working process[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10287-1011253523.htm [15] 李裕春, 时党勇, 赵远.ANSYS 11.0/LS-DYNA基础理论与工程实践[M].北京:中国水利水电出版社, 2008. [16] 蒋克强, 张遵鸥, 张培成.基于ANSYS/LS-DYNA的示位标入水冲击仿真分析[J].电子机械工程, 2012, 28(2):15-17, 21. doi: 10.3969/j.issn.1008-5300.2012.02.005JIANG Keqiang, ZHANG Zun'ou, ZHANG Peicheng. Water-entry impact simulation analysis of a position indicating radio beacon based on ANSYS/LS-DYNA[J]. Electro-Mechanical Engineering, 2012, 28(2):15-17, 21. doi: 10.3969/j.issn.1008-5300.2012.02.005 [17] 刘树红, 吴玉林, 左志钢.应用流体力学[M].北京:清华大学出版社, 2012. [18] 郭子涛, 张伟, 郭钊, 等.截卵形弹水平入水的速度衰减及空泡扩展特性[J].爆炸与冲击, 2017, 37(4):727-733. http://www.bzycj.cn/CN/abstract/abstract9775.shtmlGUO Zitao, ZHANG Wei, GUO Zhao, et al. Characteristics of velocity attenuation and cavity expansion induced by horizontal water-entry of truncated-ogive nosed projectiles[J]. Explosion and Shock Waves, 2017, 37(4):727-733. http://www.bzycj.cn/CN/abstract/abstract9775.shtml [19] 何春涛, 王聪, 魏英杰, 等.圆柱体垂直入水空泡形态试验[J].北京航空航天大学学报, 2012, 38(11):1542-1546. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201205748643HE Chuntao, WANG Cong, WEI Yingjie, et al. Vertical water entry cavity of cylinder body[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(11):1542-1546. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201205748643 [20] 邓春燕, 裴锦华.全向式气囊着陆装置缓冲过程的仿真研究[J].中国空间科学技术, 2010, 30(1):78-83. http://d.old.wanfangdata.com.cn/Periodical/zgkjkxjs201001012DENG Chunyan, PEI Jinhua. Simulation about buffer process of omni-directional-type airbag landing device[J]. Chinese Space Science and Technology, 2010, 30(1):78-83. http://d.old.wanfangdata.com.cn/Periodical/zgkjkxjs201001012 [21] 李名琦.应急气囊着水冲击特性的试验研究与数值分析[D].南京: 南京航空航天大学, 2008. doi: 10.7666/d.d053189 [22] 戴华杰, 胡振东, 咸奎成, 等.火星探测器气囊缓冲系统着陆过程仿真[J].力学季刊, 2010, 31(4):555-561. http://d.old.wanfangdata.com.cn/Periodical/lxjk201004014DAI Huajie, HU Zhendong, XIAN Kuicheng, et al. Simulation analysis for landing process of a Mars detector with airbag buffer system[J]. Chinese Quarterly of Mechanics, 2010, 31(4):555-561. http://d.old.wanfangdata.com.cn/Periodical/lxjk201004014 -






 下载:
下载: