Analysis on the deformation process of PET shock tube diaphragm
-
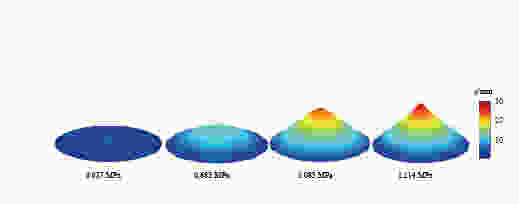
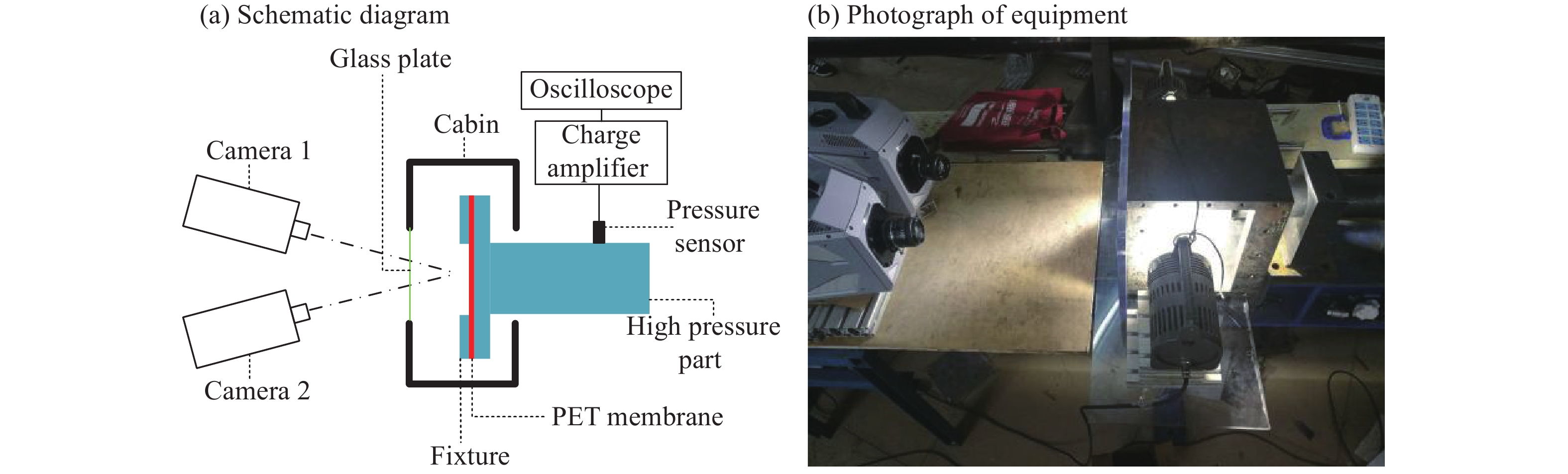
摘要: 使用聚酯薄膜作为激波管膜片,通过施加不同压力的激波管实验,获得了膜片厚度及多张膜片的组合方式对膜片所能承受最大压力的影响。利用高速相机对激波管膜片从开始变形到破坏的全过程进行拍摄,使用三维DIC软件获得膜片在变形过程中的位移场。实验发现了膜片会出现圆弧反翘并快速破坏的特别现象,并以此为特征将变形过程分为2个阶段。给出任意厚度膜片第1阶段圆弧变形的数学规律及第2阶段圆弧反翘的形状特征,以及全过程中膜片厚度变化的数学规律。Abstract: In order to investigate the effect of diaphragms thickness and combination on the maximum bearing pressure, the shock tube experiment was conducted on the PET diaphragms with different thicknesses. Two high-speed cameras were used to capture and record the whole deformation process of the PET diaphragms. The diaphragms displacement field at different moments were obtained by 3D-DIC. An unusual interesting phenomenon was observed that the diaphragms were recurved and then dramatically ruptured, and thus the diaphragm defamation was divided into two stages. The diaphragms deformation of any thickness in the first stage, and the shape characteristic of the diaphragm recurvation in the second stage as well as the thickness variation during the whole process were analyzed.
-
Key words:
- shock tube /
- deformation of diaphragm /
- PET /
- 3D-DIC
-
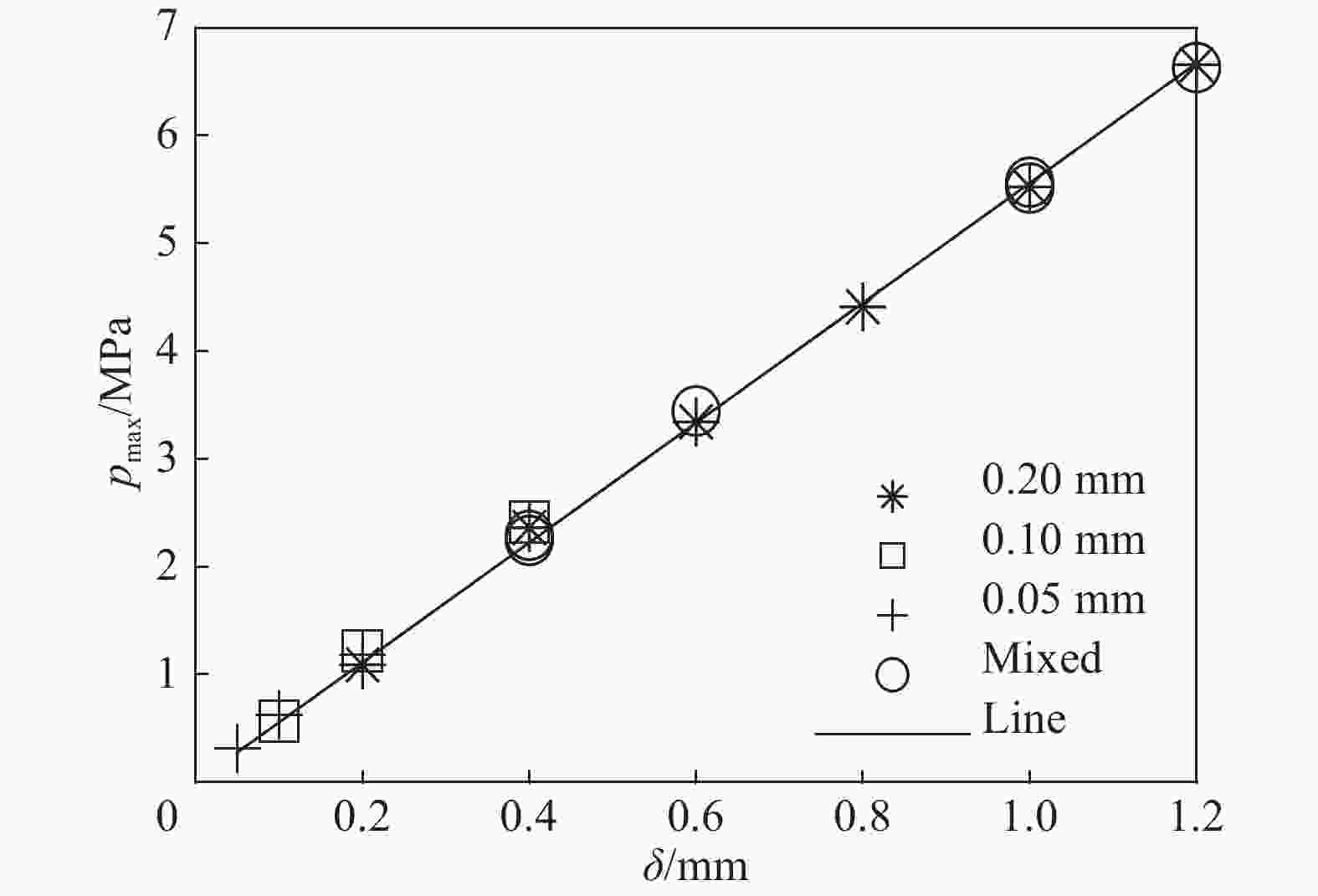
表 1 不同膜片组合及厚度的最大破坏压力
Table 1. The maximum bearing pressure of different diaphragms thickness and combinations
膜片使用数量 总厚度/mm 最大破坏压力/MPa 膜片使用数量 总厚度/mm 最大破坏压力/MPa 0.05 mm 0.1 mm 0.2 mm 0.05 mm 0.1 mm 0.2 mm 1 0 0 0.05 0.311 4 2 1 0.6 3.446 2 0 0 0.1 0.626 0 0 3 0.6 3.344 0 1 0 0.1 0.566 0 0 4 0.8 4.411 4 0 0 0.2 1.181 4 0 4 1 5.568 0 2 0 0.2 1.214 0 2 4 1 5.514 0 0 1 0.2 1.089 0 0 5 1 5.524 4 0 1 0.4 2.244 4 2 4 1.2 6.632 0 2 1 0.4 2.292 0 0 6 1.2 6.659 0 4 0 0.4 2.417 表 2 三种不同厚度膜片临界点的数据
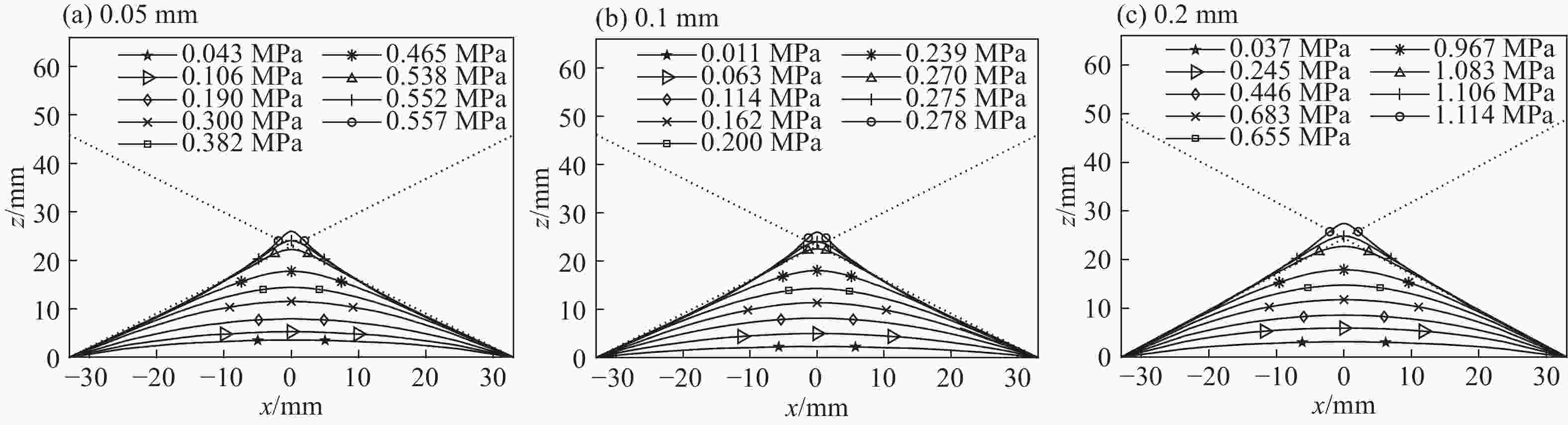
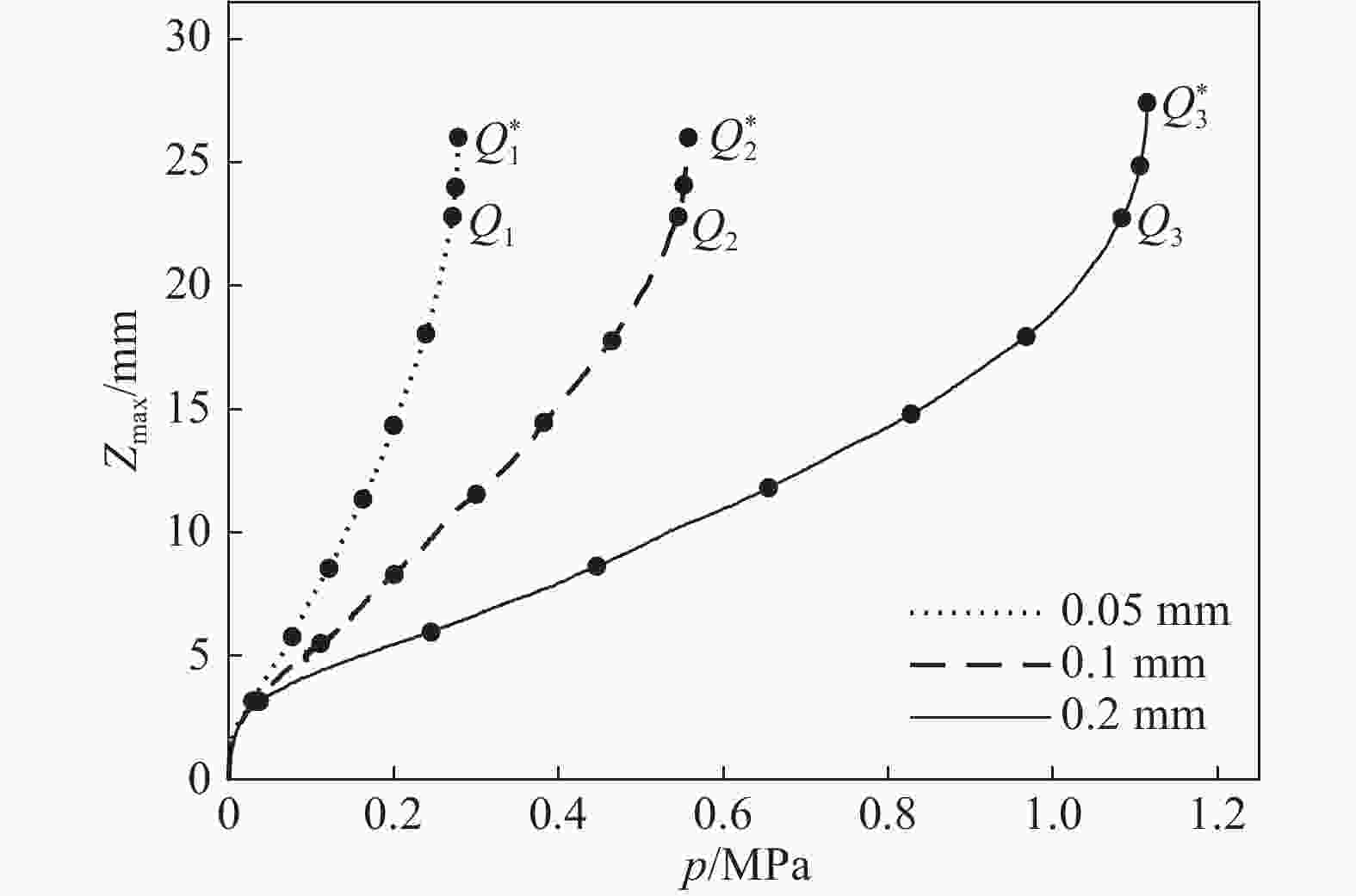
Table 2. Data of critical point in diaphragm with three different thickness
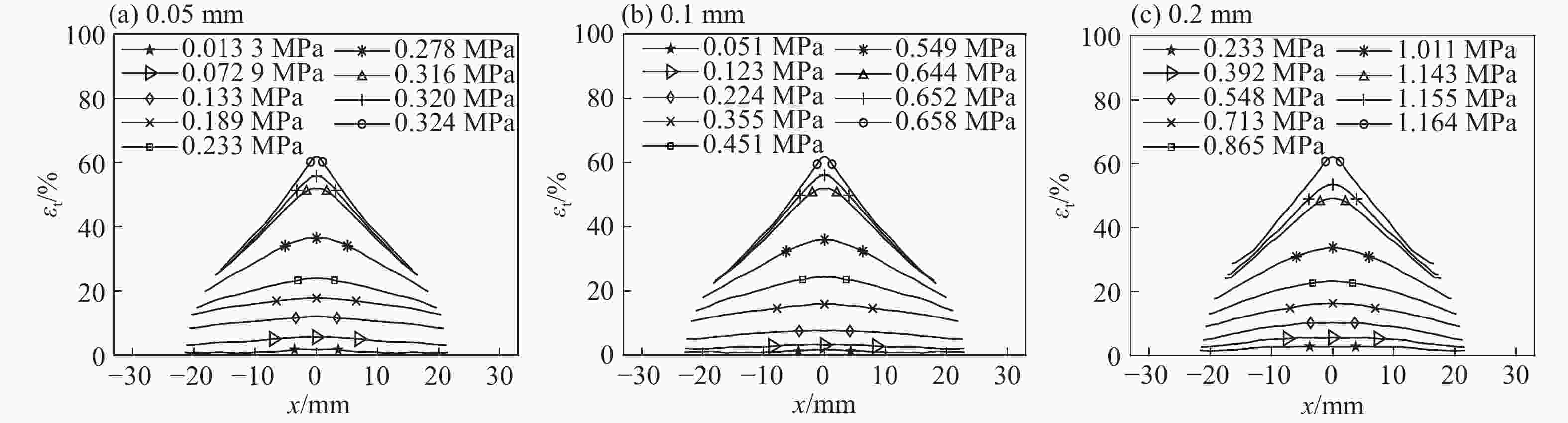
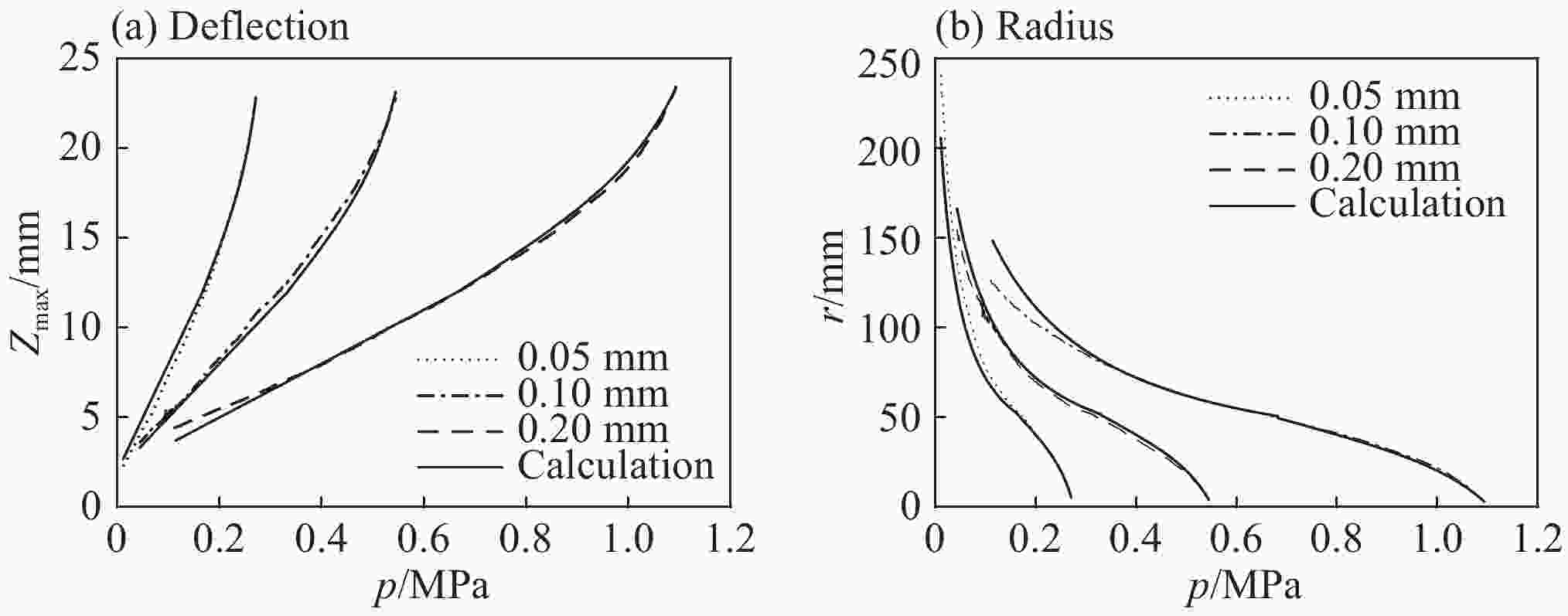
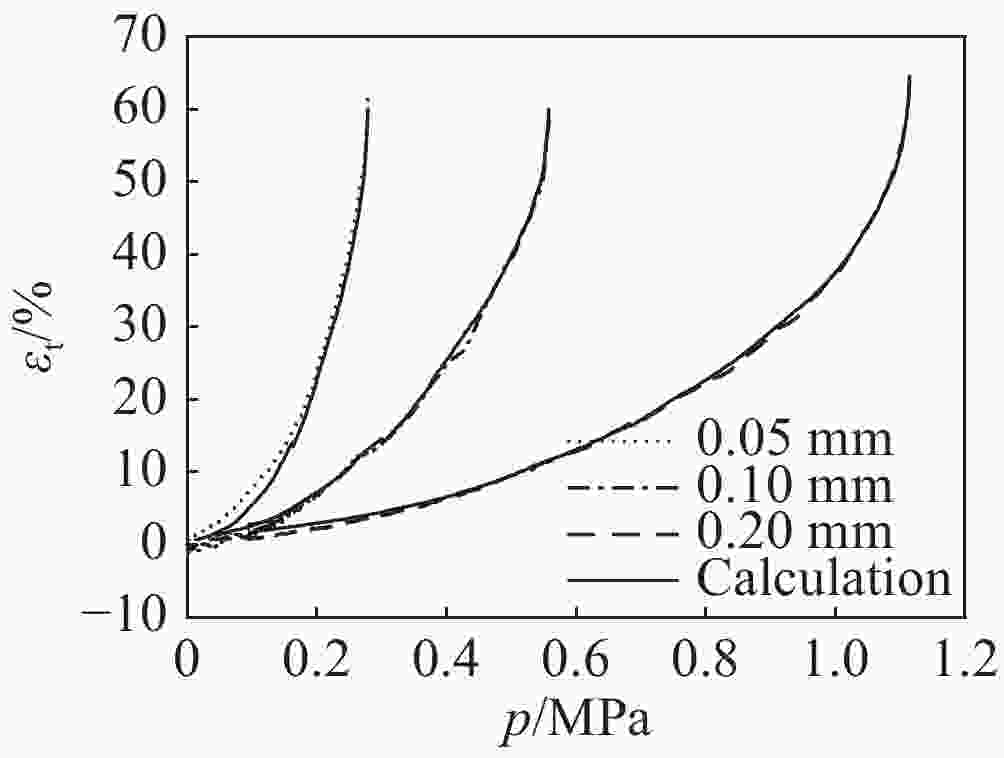
临界点 厚度/mm 压力/MPa 挠度/mm 平均挠度/mm k'/(GPa·m−1) \small$\overline {k{\rm{'}}} $/(GPa·m−1) Q1 0.05 0.271 22.81 22.84 5.42 5.440 Q2 0.1 0.545 22.95 5.45 Q3 0.2 1.08 22.75 5.45 Q1* 0.05 0.278 26.02 26.47 5.56 5.563 Q2* 0.1 0.557 26.01 5.56 Q3* 0.2 1.114 27.43 5.57 -
[1] 韩肇元, 王震球, 尹协振, 等. 用于研究双波迎面相互作用的电控双驱动激波管实验技术 [J]. 力学学报, 1982, 18(4): 86–92 doi: 10.6052/0459-1879-1982-4-1982-047HAN Zhaoyuan, WANG Zhengqiu, YIN Xiezhen, et al. An experimental technique of electrical controlled double driver shock tube for studying head-on moving shock-bow shock interaction [J]. Chinese Journal of Theoretical and Applied Mechanics, 1982, 18(4): 86–92 doi: 10.6052/0459-1879-1982-4-1982-047 [2] 黄文斌, 谭多望, 闫石, 等. 电破膜式激波管的破膜装置: CN201859050U [P]. 2011-02-16. [3] NGUYEN T T N, WILGEROTH J M, PROUD W G. Controlling blast wave generation in a shock tube for biological applications [C]// Journal of Physics: Conference Series, 2014. DOI: 10.1088/1742-6596/500/14/142025. [4] GHARABABAEI H, DARVIZEH A. Experimental and analytical investigation of large deformation of thin circular plates subjected to localized and uniform impulsive loading [J]. Mechanics Based Design of Structures & Machines, 2010, 38(2): 171–189. doi: 10.1080/15397730903554633 [5] BRADLEY J N, LINDSAY R B. Shock waves in chemistry and physics [J]. Physics Today, 1963, 16(8): 60. doi: 10.1063/1.3051077 [6] BARSOUM I, FALESKOG J. Rupture mechanisms in combined tension and shear—experiments [J]. International Journal of Solids & Structures, 2007, 44(6): 1768–1786. doi: 10.1016/j.ijsolstr.2006.09.031 [7] ROTHKOPF E M. Diaphragm opening process in shock tubes [J]. Physics of Fluids, 1974, 17(6): 1169–1173. doi: 10.1063/1.1694860 [8] CAMPBELL G A, KIMBER G M, NAPIER D H. Bursting of diaphragms as related to the operation of shock tubes [J]. Journal of Scientific Instruments, 1965, 42(6): 381. doi: 10.1088/0950-7671/42/6/303 [9] 佟富强, 刘宝璋. 聚酯(PET)薄膜形变性能的研究 [J]. 包装工程, 1997(1): 26–28TONG Fuqiang, LIU Baozhang, ZHANG Jinlong, et al. Study on the deforming properties of the PET film [J]. Packaging Engineering, 1997(1): 26–28 [10] 黄官强, 鞠开阳, 朱强, 等. PET膜片压力胀型失效试验与有限元分析 [J]. 现代制造工程, 2015(10): 88–92 doi: 10.3969/j.issn.1671-3133.2015.10.020HUANG Guanqiang, JU Kaiyang, ZHU Qiang, et al. Experiment and finite element analysis of pressure bulging for PET film [J]. Modern Manufacturing Engineering, 2015(10): 88–92 doi: 10.3969/j.issn.1671-3133.2015.10.020 -







 下载:
下载: