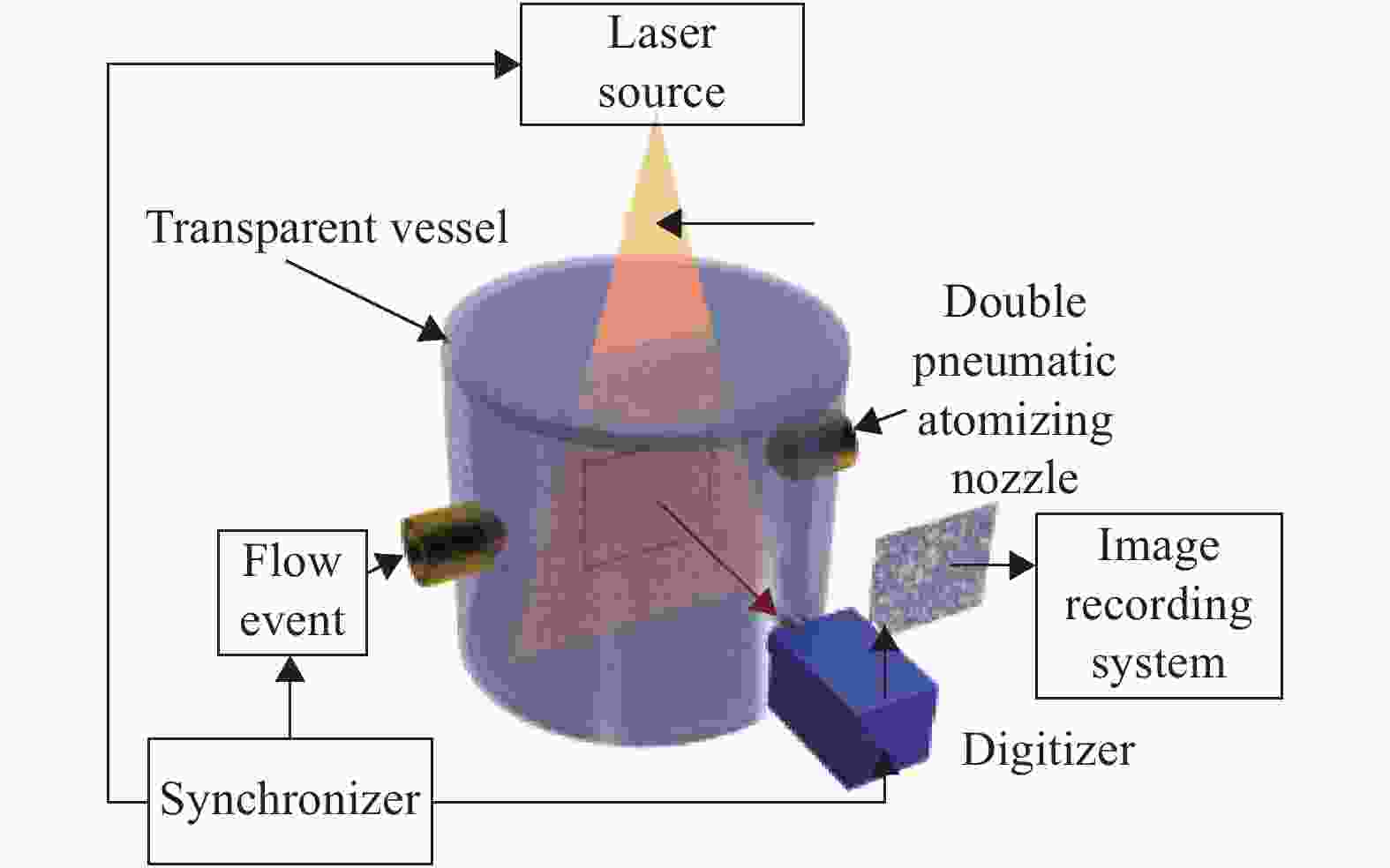
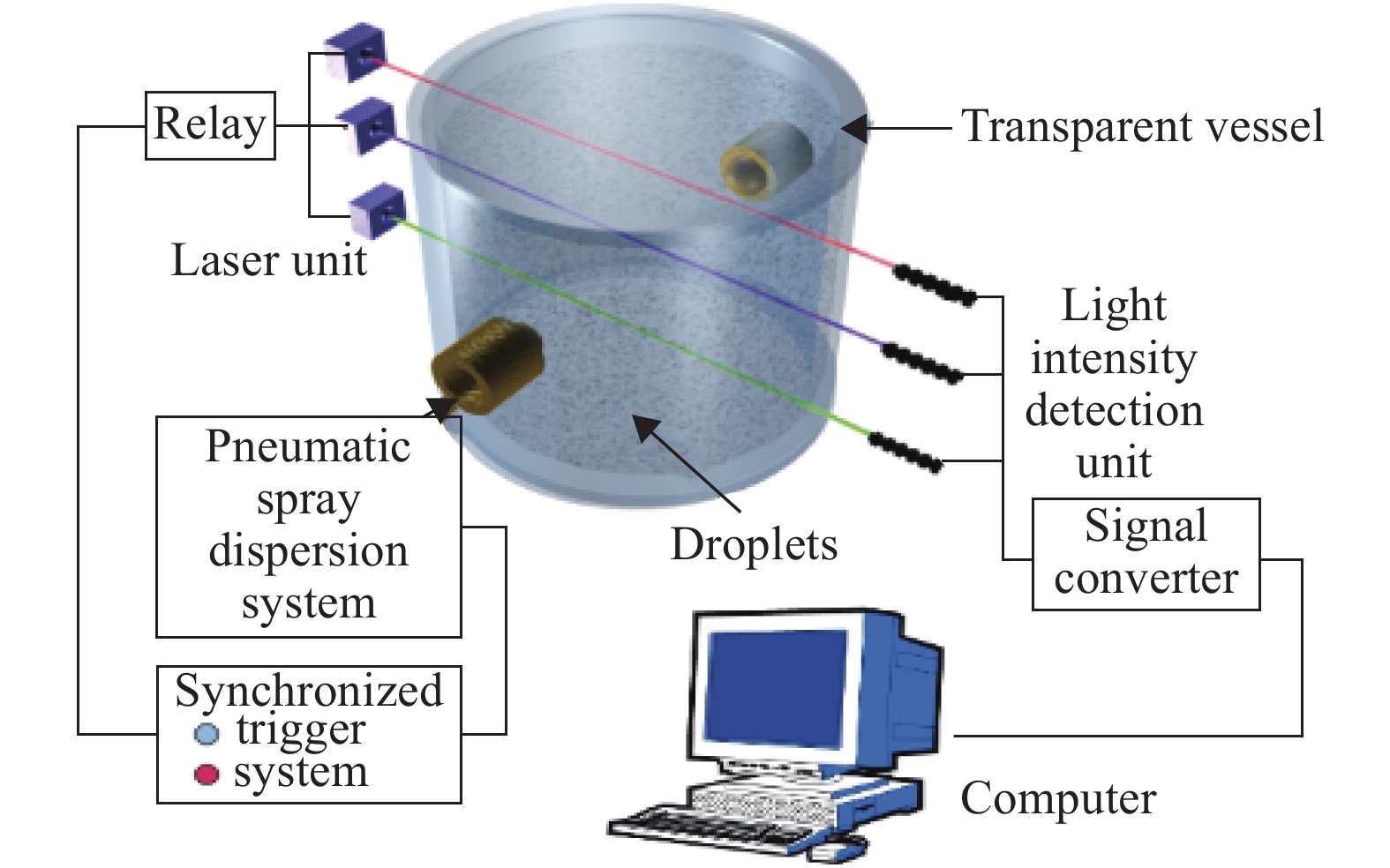
Influence of pre-ignition turbulence intensity on n-pentane mists explosion
-
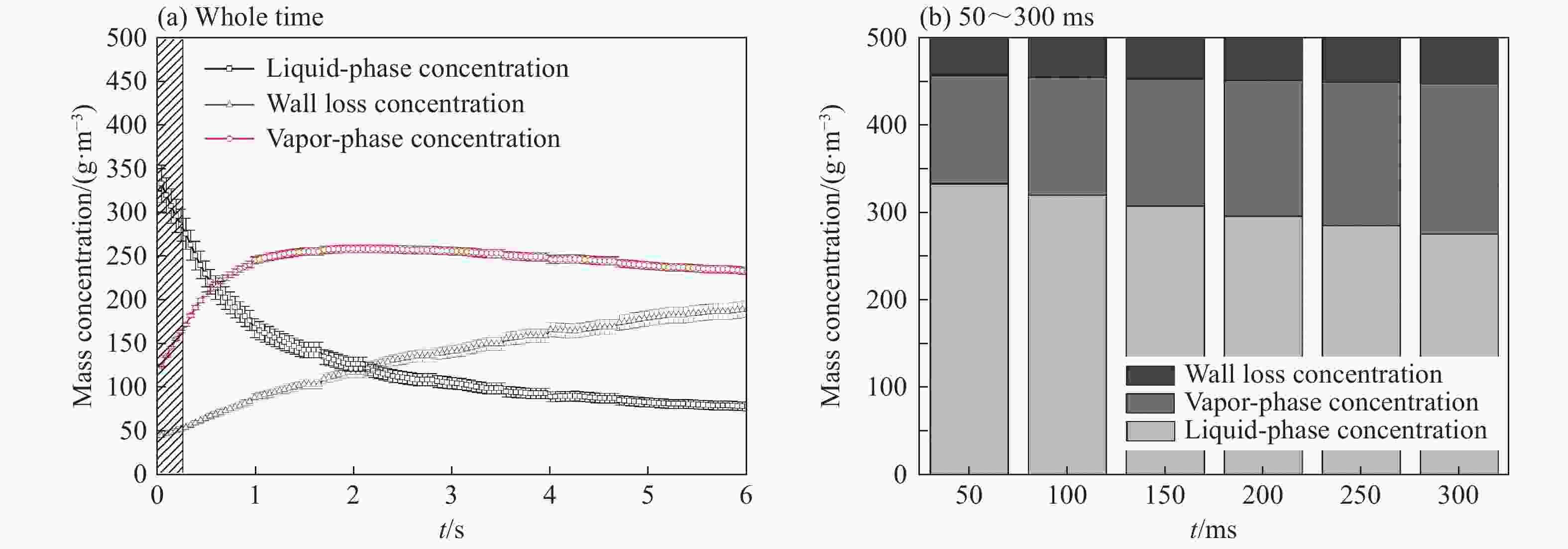
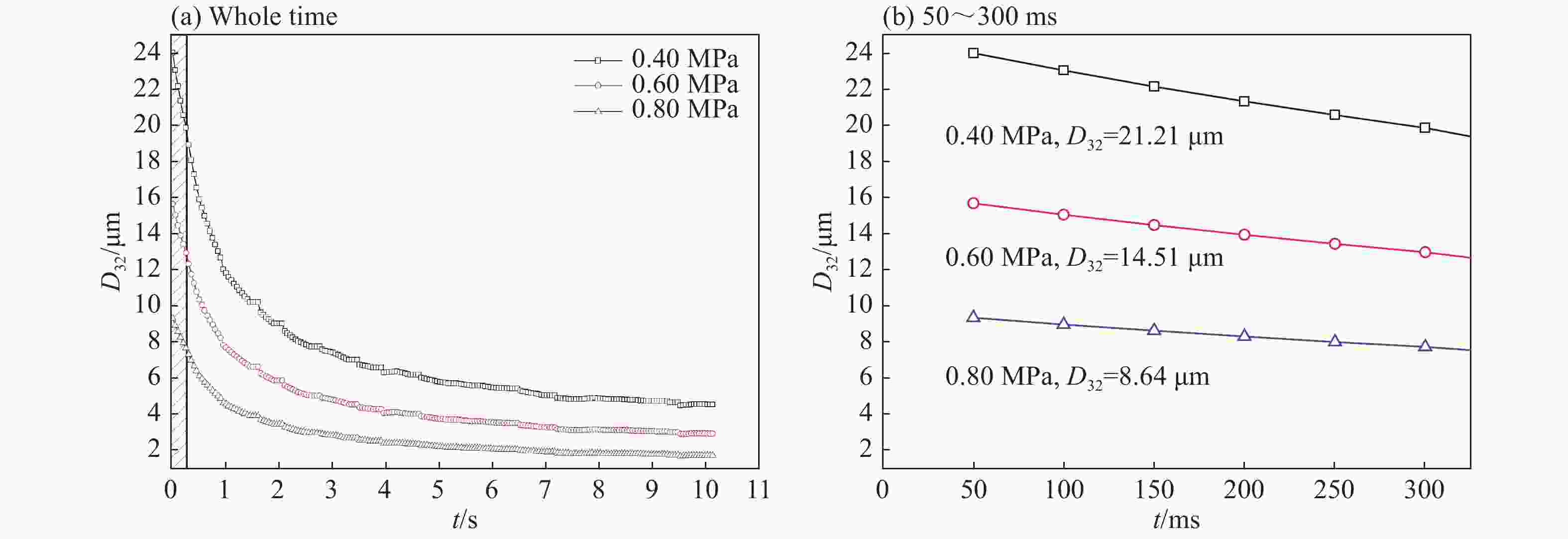
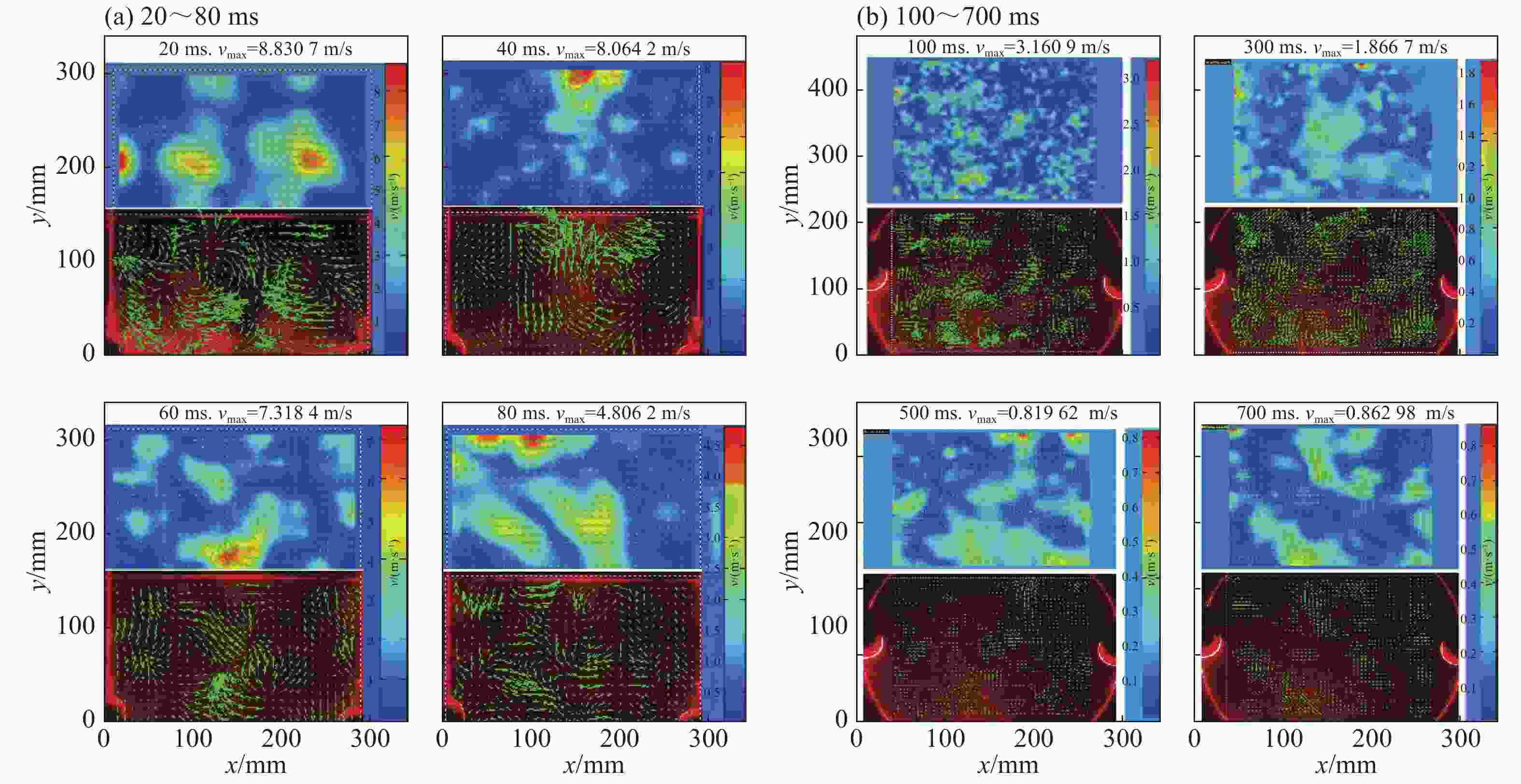
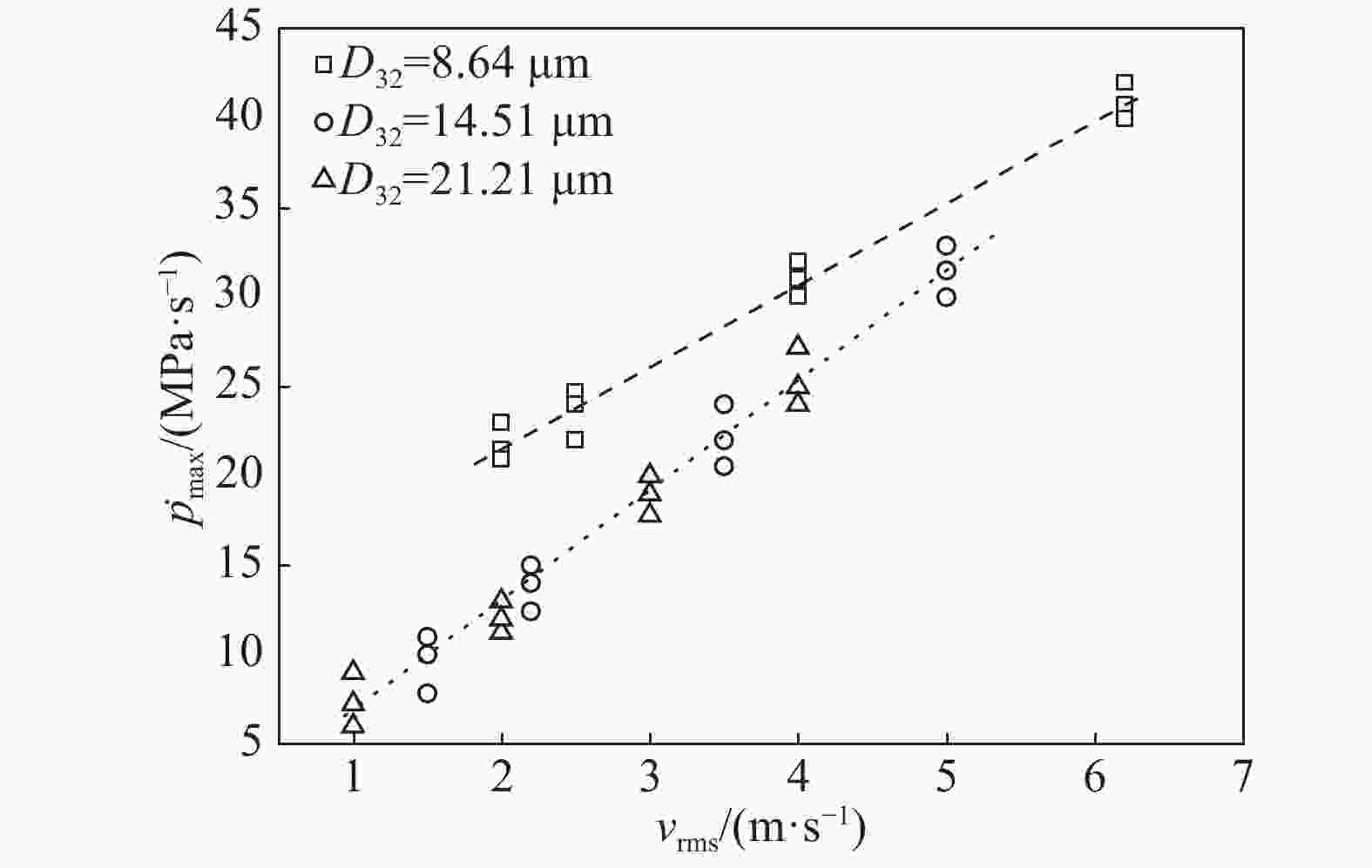
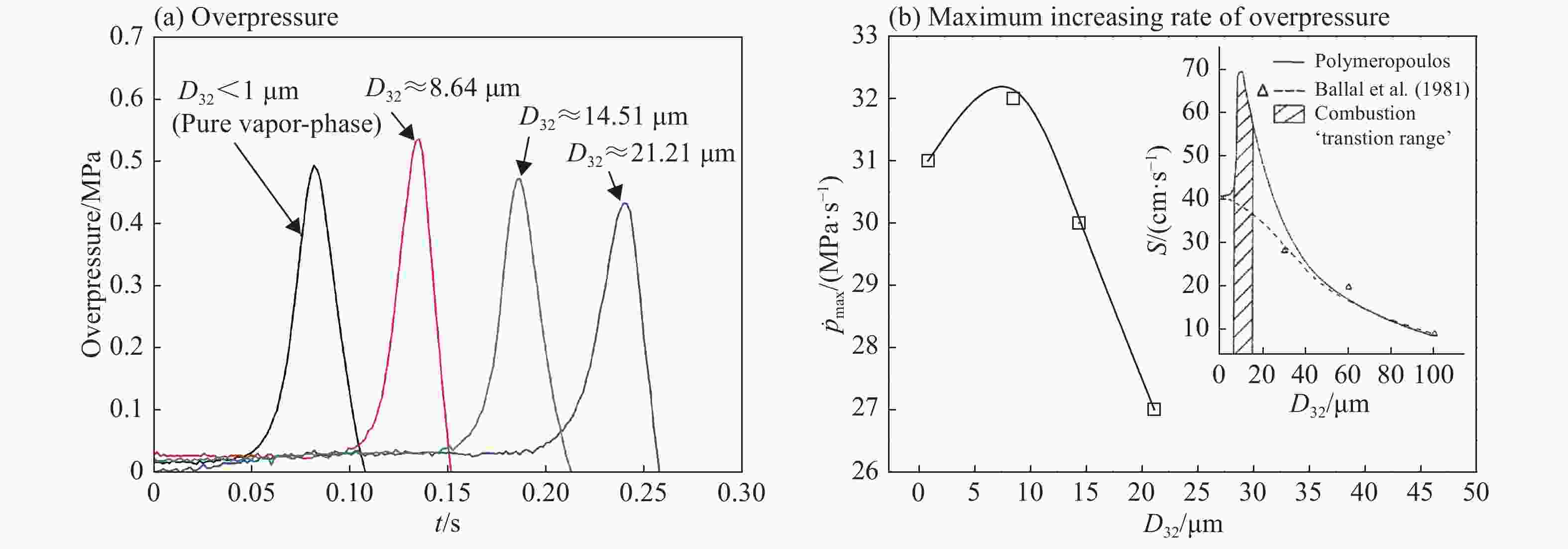
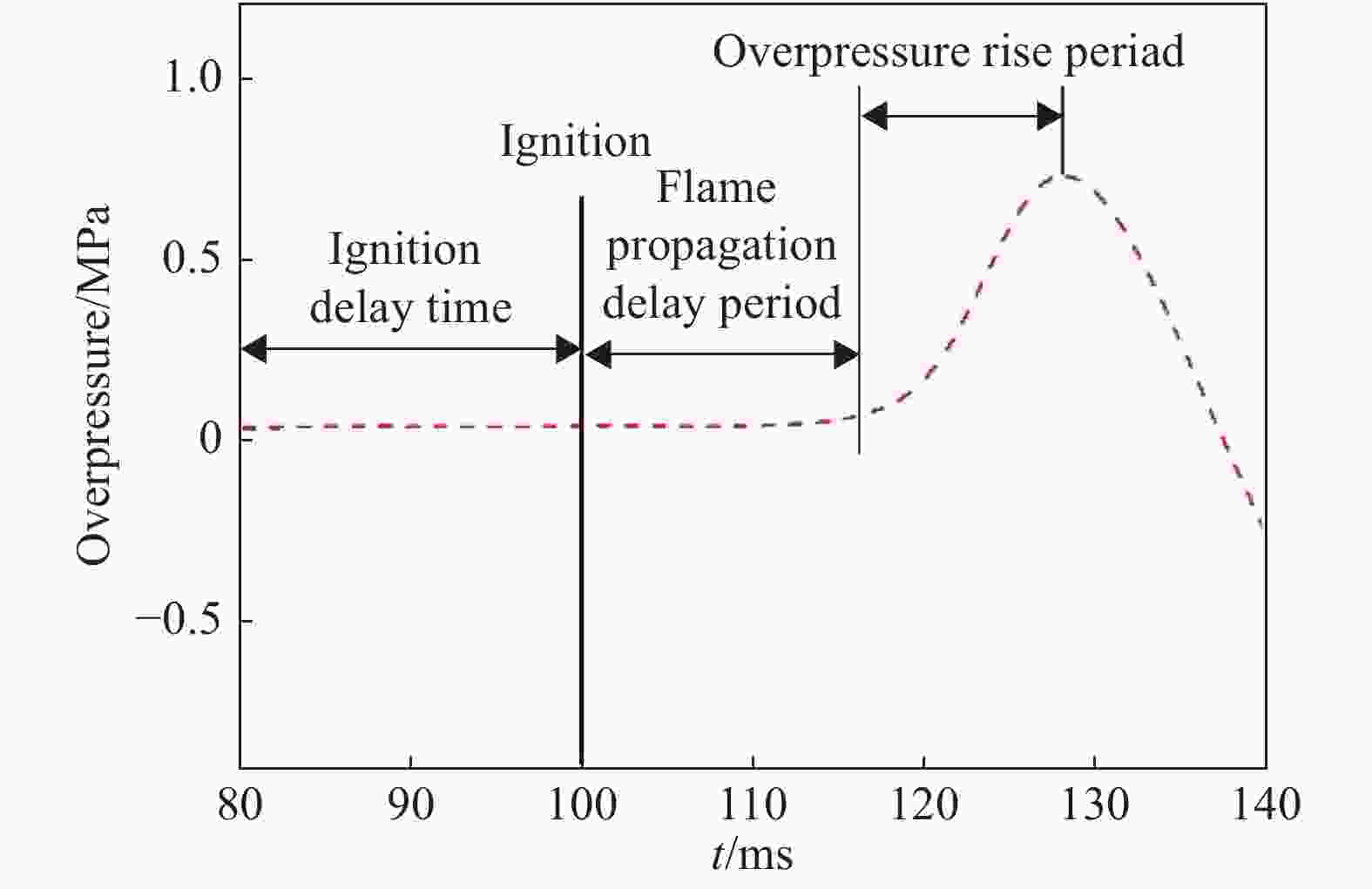
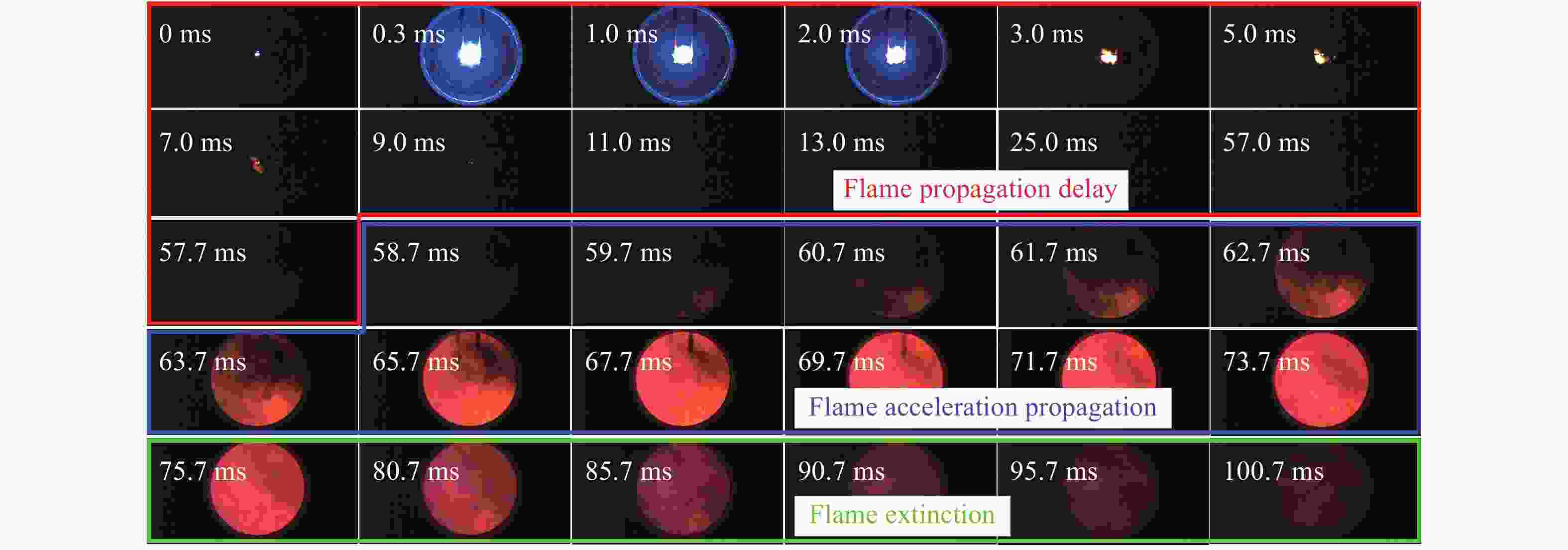
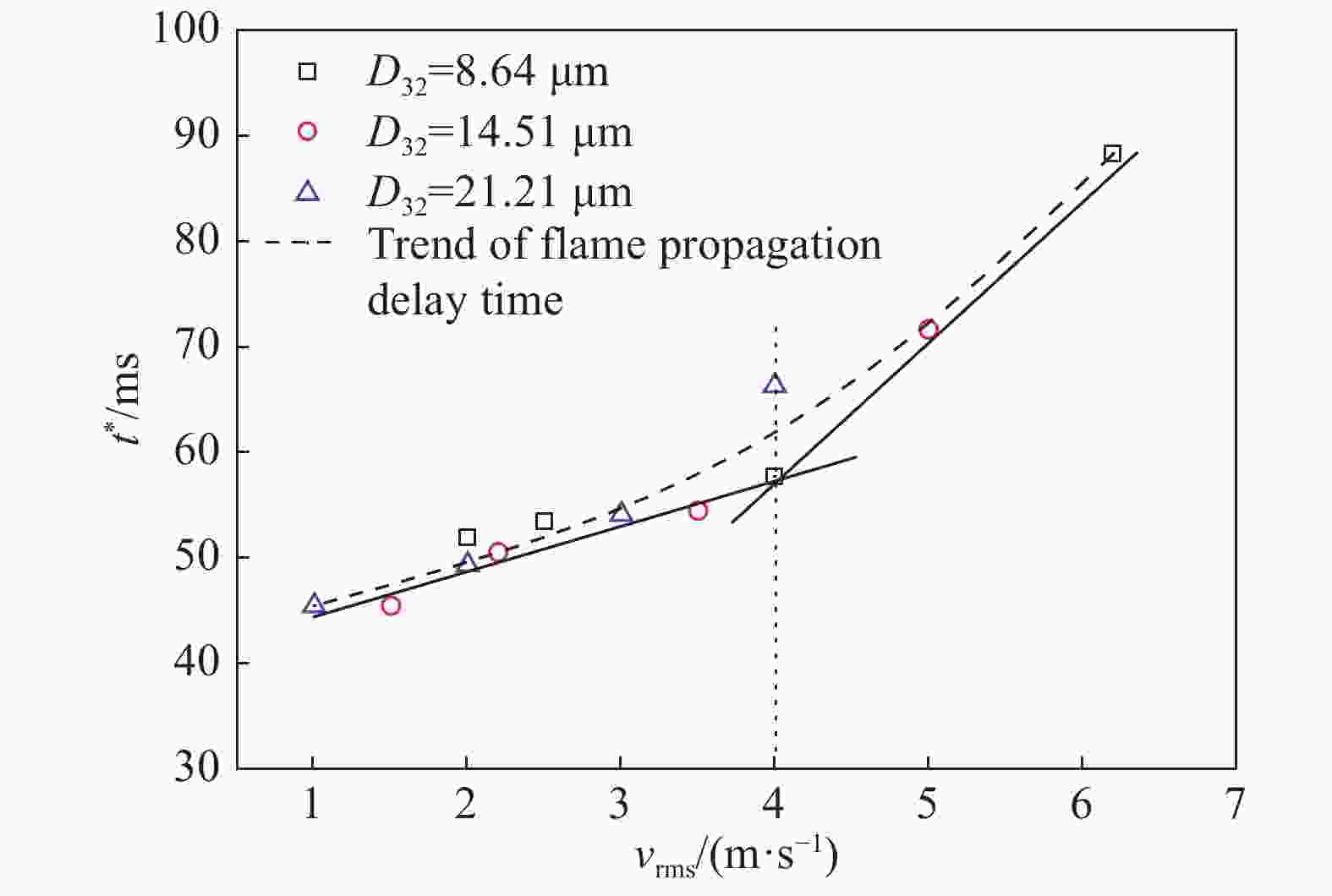
摘要: 以正戊烷云雾为研究对象,进行预点火湍流对云雾爆炸参数影响规律的实验研究。首先通过不同气动压力进行喷雾,获得平均特征直径(SMD)分别为 21.21、14.51 和 8.64 μm 的正戊烷云雾,并得到不同气动压力预点火的湍流均方根速度;随后在 20 L 云雾爆炸参数测量系统中实验获得预点火湍流对正戊烷云雾蒸发速率、爆炸超压峰值、压力上升速率和火焰传播延迟时间的影响。结果表明:(1) 对于圆柱形罐体对称式双喷头分散系统,流场环境可近似认定为零平均速率湍流场;在0.4、0.6和0.8 MPa的气动压力喷雾50 ms的分散作用下,在100~250 ms内,湍流均方根速度在1.0~6.2 m/s范围内,平均湍流积分尺度在40~72 mm范围内,湍流最大湍流尺度的雷诺数在8 000~15 000范围内,柯尔莫哥洛夫微尺度在0.03~0.1 mm范围内;(2) 对于较小的液滴群,随湍流强度的增加,液滴群的蒸发速率有更为明显的提升;(3) 对比云雾三种SMD,粒径8.64 μm的超压峰值与最大压力上升速率随湍流强度增长趋势更显著,并发生爆炸强度显著提升现象,即存在“转变区域”(transition range)现象;(4) 对于SMD在8~22 μm范围内,湍流均方根速度处于1.0~4.0 m/s时为火焰传播延迟时间的低增长阶段,湍流均方根速度处于4.0~6.2 m/s时为火焰传播延迟时间的高增长阶段,湍流强度与火焰传播延迟时间在相应的两个湍流强度阶段范围内呈线性增长。Abstract: In this paper we investigated the influence of the pre-ignition turbulence intensity on the explosion parameters of n-pentane mists. By using 0.4, 0.6 and 0.8 MPa of pneumatic pressure spray, we obtained n-pentane mists with the Sauter mean diameter (SMD) of 21.21, 14.51 and 8.64 μm, and at the same time, the pre-ignition turbulence intensity under different pneumatic pressures. Then, in a 20 L mists explosion parameter measuring system for experimental research, we aquired the influence of the pre-ignition turbulence on the evaporation rate, the peak explosion overpressure, the explosion pressure rise rate and the ignition delay time of n-pentane mists. The results showed that, the average turbulence velocity of the enviromental fluid field was zero. The smaller the droplet size was, the more obvious was the increase of the evaporation rate of the mists with the increase of the turbulence intensity. At the same time, for the SMDs of 14.51 and 21.21 μm, the peak pressure and the maximum pressure rise rate increased more obviously with the SMD of 8.64 μm, and the explosion intensity was significantly strong, suggesting the existence of a transition range. For the SMDs in the range of 8−22 μm, the mean square turbulence velocity in 1.0−4.0 m/s was the low growth stage of the flame propagation delay time, whereas that in 4.0−6.2 m/s was the high growth stage. The turbulence intensity and the flame propagation delay time exhibited a linear growth in both stages.
-
表 1 正戊烷云雾湍流强度及浓度粒径实验统计结果
Table 1. Experiment results of turbulence intensity and concentration
气动压力/
MPa时刻/
msvrms/
(m·s−1)D32/
μm质量浓度/(g·m−3) 总体 液相 气相 0.8 100 6.2 8.64 454 340 137 150 4.0 452 327 148 200 2.5 451 315 158 250 2.0 449 304 167 0.6 100 5.0 14.51 454 320 134 150 3.5 452 307 145 200 2.2 451 296 151 250 1.5 449 285 164 0.4 100 4.0 21.21 454 299 132 150 3.0 452 288 142 200 2.0 451 277 152 250 1.0 449 267 160 注:vrms为流场均方根速度 表 2 不同气动喷雾压力下湍流积分尺度及雷诺数
Table 2. Average turbulence integral scale and Reynolds numbers at different dispersing air pressures
时间/ms ${\ell _0}$/mm $Re_{{\ell _0}}^{}$ 0.8 MPa 0.6 MPa 0.4 MPa 0.8 MPa 0.6 MPa 0.4 MPa 100 40 45 48 16 300 15 600 15 000 150 55 57 58 12 600 12 000 11 700 200 65 68 70 9 200 8 700 8 400 250 67 69 72 8 600 8 500 8 000 -
[1] 白春华, 梁慧敏, 李建平. 云雾爆轰[M]. 北京: 科学出版社, 2012: 1.BAI Chunhua, LIANG Huiming, LI Jianping. Spray detonation[M]. Beijing: Science Press, 2012: 1. [2] 姚干兵, 解立峰, 刘家骢. 液体碳氢燃料云雾爆轰特性的实验研究 [J]. 爆炸与冲击, 2006, 26(6): 543–549 doi: 10.3321/j.issn:1001-1455.2006.06.012YAO Ganbing, XIE Lifeng, LIU Jiacong. Experimental study on detonation characteristics of liquid fuel-air mixtures [J]. Explosion and Shock Waves, 2006, 26(6): 543–549 doi: 10.3321/j.issn:1001-1455.2006.06.012 [3] 沈晓波, 鲁长波, 李斌, 等. 液体燃料云雾爆轰参数实验 [J]. 爆炸与冲击, 2012, 32(1): 108–112SHEN Xiaobo, LU Changbo, LI Bin, et al. An experimental study of detonation parameters of liquid fuel drops cloud [J]. Explosion and Shock Waves, 2012, 32(1): 108–112 [4] LIU Q M, BAI C H, D W X, et al. Deflagration-to-detonation transition in isopropyl nitrate mist/air mixtures [J]. Combustion, Explosion, and Shock Waves, 2011, 47(4): 448–456. doi: 10.1134/S0010508211040083 [5] LIU Q M, BAI C H, JIANG L, et al. Deflagration-to-detonation transition in nitromethane mist/aluminum dust/air mixtures [J]. Combustion and Flame, 2010, 157(1): 106–117. doi: 10.1016/j.combustflame.2009.06.026 [6] MOEN I. Transition to detonation in fuel-air explosive clouds [J]. Journal of Hazardous Materials, 1993, 33(2): 159–192. doi: 10.1016/0304-3894(93)85052-G [7] STAMPS D W, SLEZAK S E, TIESZEN S R. Observations of the cellular structure of fuel-air detonations [J]. Combustion and Flame, 2006, 144(1): 289–298. [8] SANTON R C. Mist fires and explosions—an incident survey [C]// IChemE Hazards XXI Symposium & Workshop. Manchester, 2009. [9] ZABETAKIS M G. Flammability characteristics of combustible gases and vapors: BULL-627[R]. Washington DC: USBM, 1965. [10] BURGOYNE J H, COHEN L. The effect of drop size on flame propagation in liquid aerosols [J]. Proceedings of the Royal Society of London: Series A: Mathematical and Physical Sciences, 1954, 225(1162): 375–392. [11] FAETH G M, OLSON D R. The ignition of hydrocarbon fuel droplets in air[R]. SAE, 1968. [12] WILLIAMS F A. Mono-disperse spray deflagration [J]. Progress in Astronautics and Rocketry, 1960, 2: 223. [13] 王悦, 白春华. 乙醚云雾场燃爆参数实验研究 [J]. 爆炸与冲击, 2016, 36(4): 497–502WANG Yue, BAI Chunhua. Experimental research on explosion parameters of diethyl ether mist [J]. Explosion and Shock Waves, 2016, 36(4): 497–502 [14] 王悦, 白春华, 李斌, 等. 正癸烷云雾气液两相浓度对其燃爆参数的影响 [J]. 含能材料, 2015, 23(7): 663–669WANG Yue, BAI Chunhua, LI Bin, et al. Influence of the gas-liquid two-phase concentrations of n-decane sprays on its explosion parameters [J]. Chinese Journal of Energetic Materials, 2015, 23(7): 663–669 [15] LIU X L, ZHANG Q, WANG Y. Influence of vapor-liquid two-phase n-hexane/air mixtures on flammability limit and minimum ignition energy [J]. Industrial & Engineering Chemistry Research, 2014, 53(32): 12856–12865. [16] LIU X L, WANG Y, ZHANG Q. A study of the explosion parameters of vapor-liquid two - phase JP-10/air mixtures [J]. Fuel, 2016, 165: 279–288. doi: 10.1016/j.fuel.2015.10.081 [17] LIU X L, ZHANG Q, WANG Y. Influence of particle size on the explosion parameters in two-phase vapor-liquid n-hexane/air mixtures [J]. Process Safety and Environmental Protection, 2015, 95: 184–194. doi: 10.1016/j.psep.2015.03.006 [18] LIU X L, ZHANG Q, WANG Y. Influence of vapor-liquid two-phase n-heptane on the explosion parameters in air [J]. Combustion Science and Technology, 2015, 187(12): 1879–1904. doi: 10.1080/00102202.2015.1069282 [19] SCHEID M, GEIßLER A, KRAUSE U. Experiments on the influence of pre-ignition turbulence on vented gas and dust explosions [J]. Journal of Loss Prevention in the Process Industries, 2006, 19(2-3): 194–199. doi: 10.1016/j.jlp.2005.04.005 [20] ANDREWS G E, DRADLEY D, LWAKABAMBA S B. Turbulence and turbulent flame propagation -a critical appraisal [J]. Combustion and Flame, 1975, 24: 285–304. doi: 10.1016/0010-2180(75)90163-7 [21] BRADLEY D, MITCHESON A. The venting of gaseous explosions in spherical vessels: I-theory [J]. Combustion and flame, 1978, 32: 221–236. doi: 10.1016/0010-2180(78)90098-6 [22] CHIPPET S. Modeling of vented deflagrations [J]. Combustion and Flame, 1984, 55(2): 127–140. doi: 10.1016/0010-2180(84)90022-1 [23] LIU X L, ZHANG Q. Influence of turbulent flow on the explosion parameters of micro-and nano-aluminum powder-air mixtures [J]. Journal of Hazardous Materials, 2015, 299: 603–617. doi: 10.1016/j.jhazmat.2015.07.068 [24] PRTERS N. The turbulent burning velocity for large-scale and small-scale turbulence [J]. Journal of Fluid Mechanics, 1999, 384: 107–132. doi: 10.1017/S0022112098004212 [25] TENNEKES H. Simple model for the small-scale structure of turbulence [J]. Physics of Fluids, 1968, 11: 669–671. doi: 10.1063/1.1691966 [26] POLYMEROPOULOS C E. Flame propagation in aerosols of fuel droplets, fuel vapor and air [J]. Combustion Science and Technology, 1984, 40(5/6): 217–232. -






 下载:
下载: