Wave propagation characteristics and parameter analysis of the distributed energy absorption system of trains
-
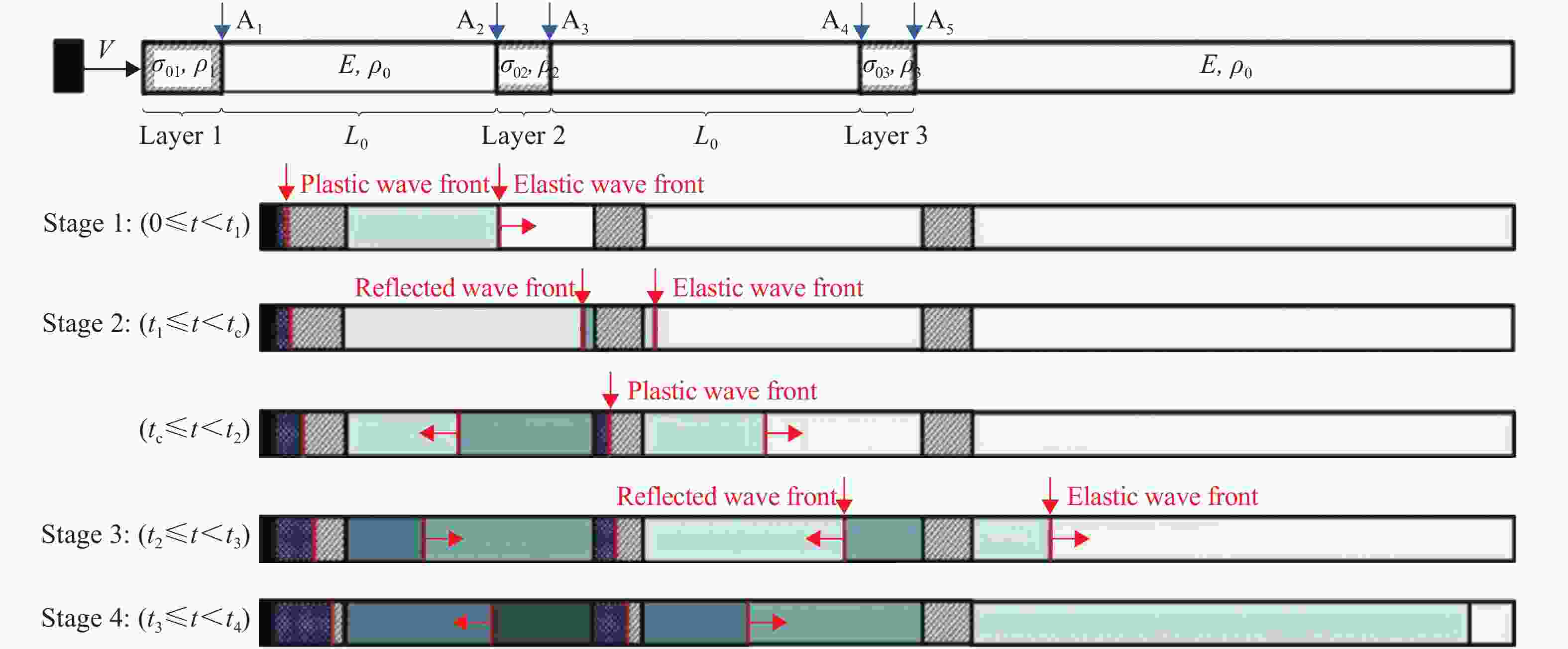
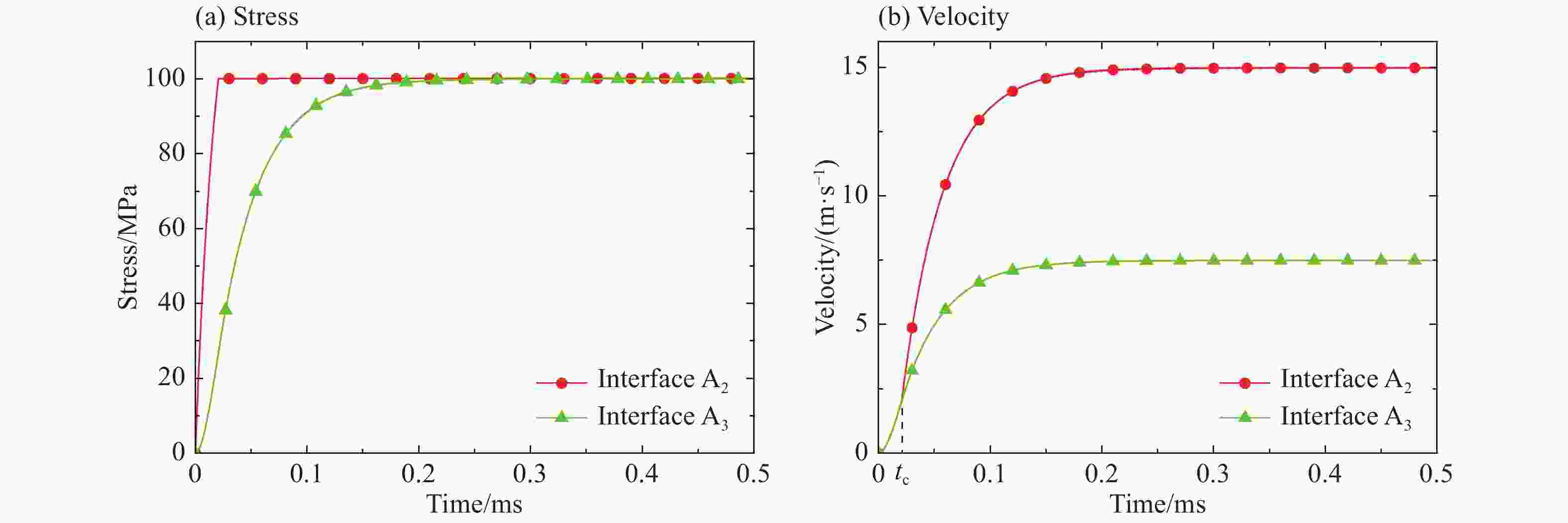
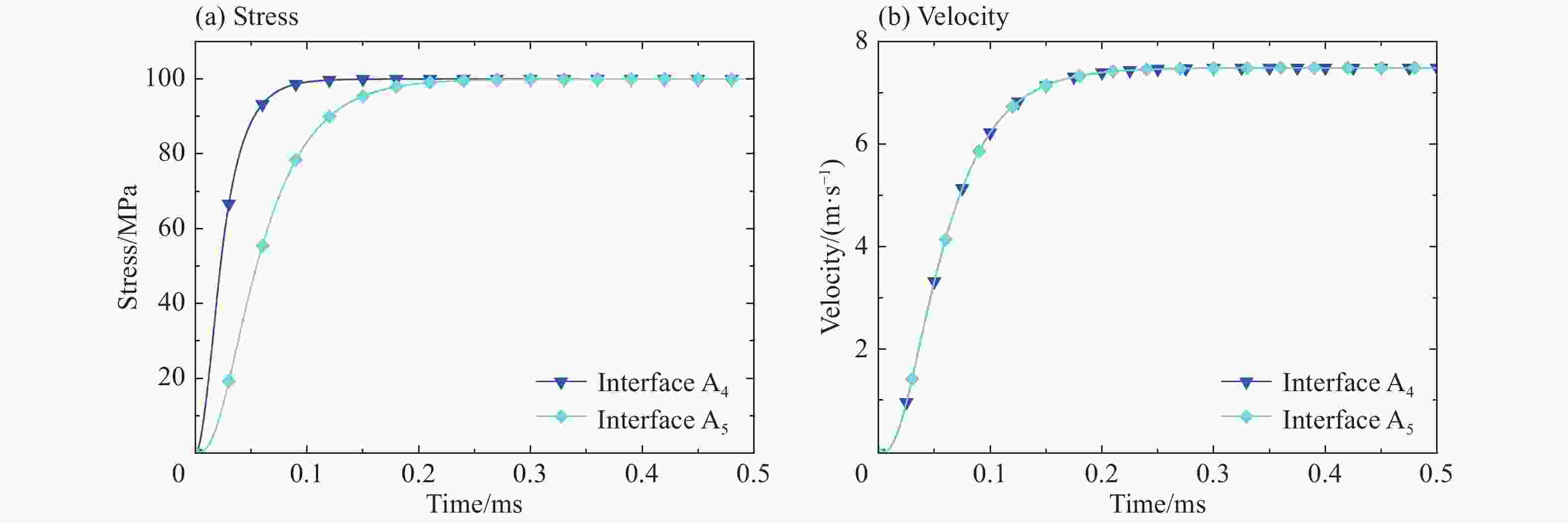
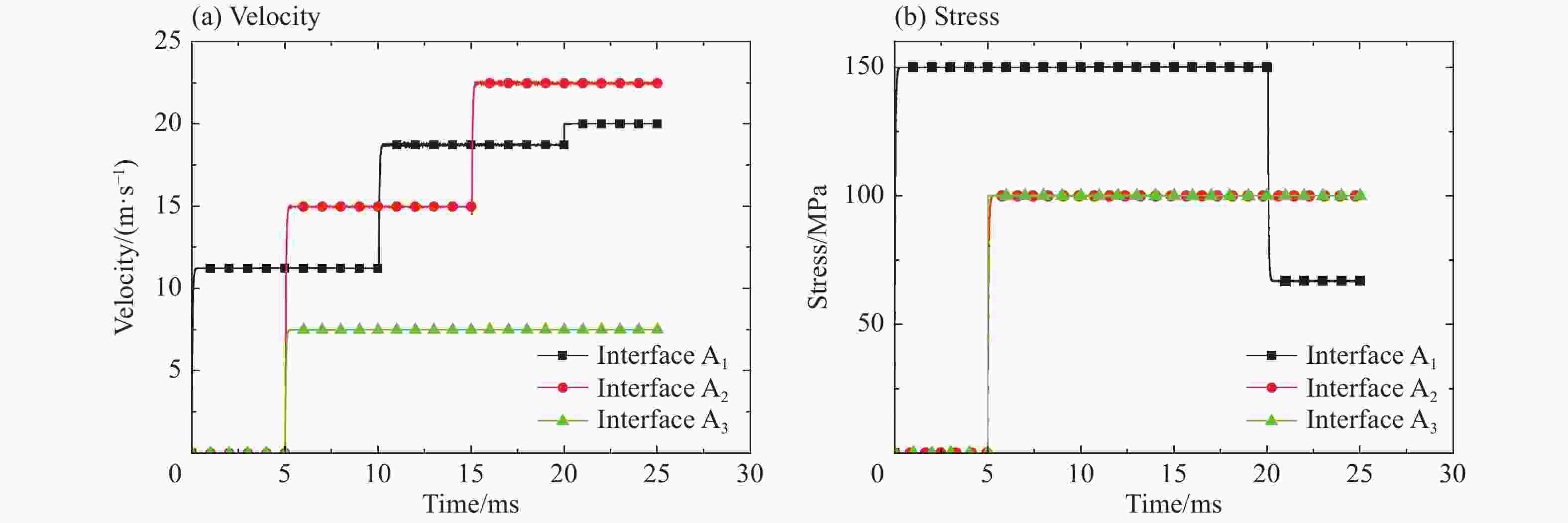
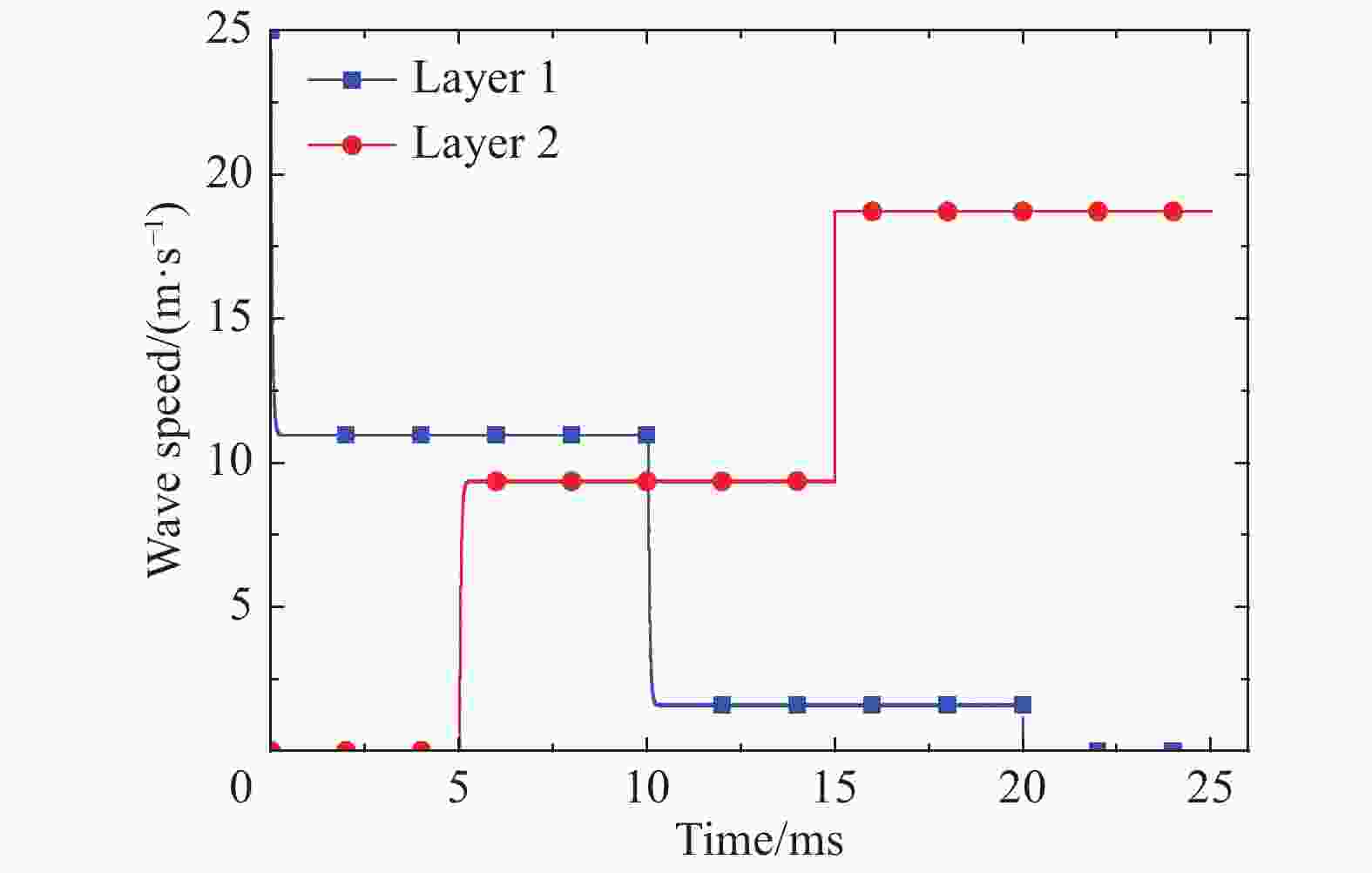
摘要: 建立了考虑车厢中弹性波传播影响的列车分布式吸能系统的简化理论模型。基于一维应力波理论,对碰撞过程中各吸能器的响应进行了理论分析,得到相关的控制方程并求解。观察到各吸能器界面上典型的阶段性、平台样的速度响应,并分析了其机理,进而对如何合理设置和排布吸能器进行了分析。结果表明:对于相邻的吸能器,碰撞前端吸能器的压垮强度应高于后端,否则后端吸能器无法同时发挥作用;各吸能器的平台应力的大小和排布是决定吸能系统作用效果的控制参量,能够决定各吸能器的吸能时长和吸能总量。具体分析了相邻吸能器的平台应力分布对系统吸能性能的影响,得到了在所研究的情况下使总吸能量最大的优化设计参数。该研究可为列车分布式吸能系统的优化设计提供理论指导。Abstract: In this study we established a simplified theoretical model of the distributed energy absorption system of trains with the influence of the propagation of elastic waves in the train carriage taken into account. Based on the one-dimensional stress wave theory, the responses of energy absorbers in the collision process were analyzed and the governing equations were obtained and solved. The typical stage and platform response of the velocities on the interfaces of each energy absorber was observed and the mechanism was revealed. The analysis about how to set up and arrange the energy absorbing devices was also carried out. The results show that the crushing strength of the front one should be higher than that of the rear one for the adjacent energy absorbers; otherwise the energy absorber at the rear end cannot work at the same time. The plateau stress and its arrangement of each absorber determine the performance of the energy absorption system, which can thereby determine the duration of the energy absorption and the total energy absorption of each energy absorber. The influence of the plateau stress distribution of the adjacent energy absorbers on the energy absorption performance of the system was analyzed in detail, and the optimal design parameter that maximizes the total energy consumption was obtained. Our study can serve as theoretical guidance for the train’s optimization design of the distributed energy absorption system.
-
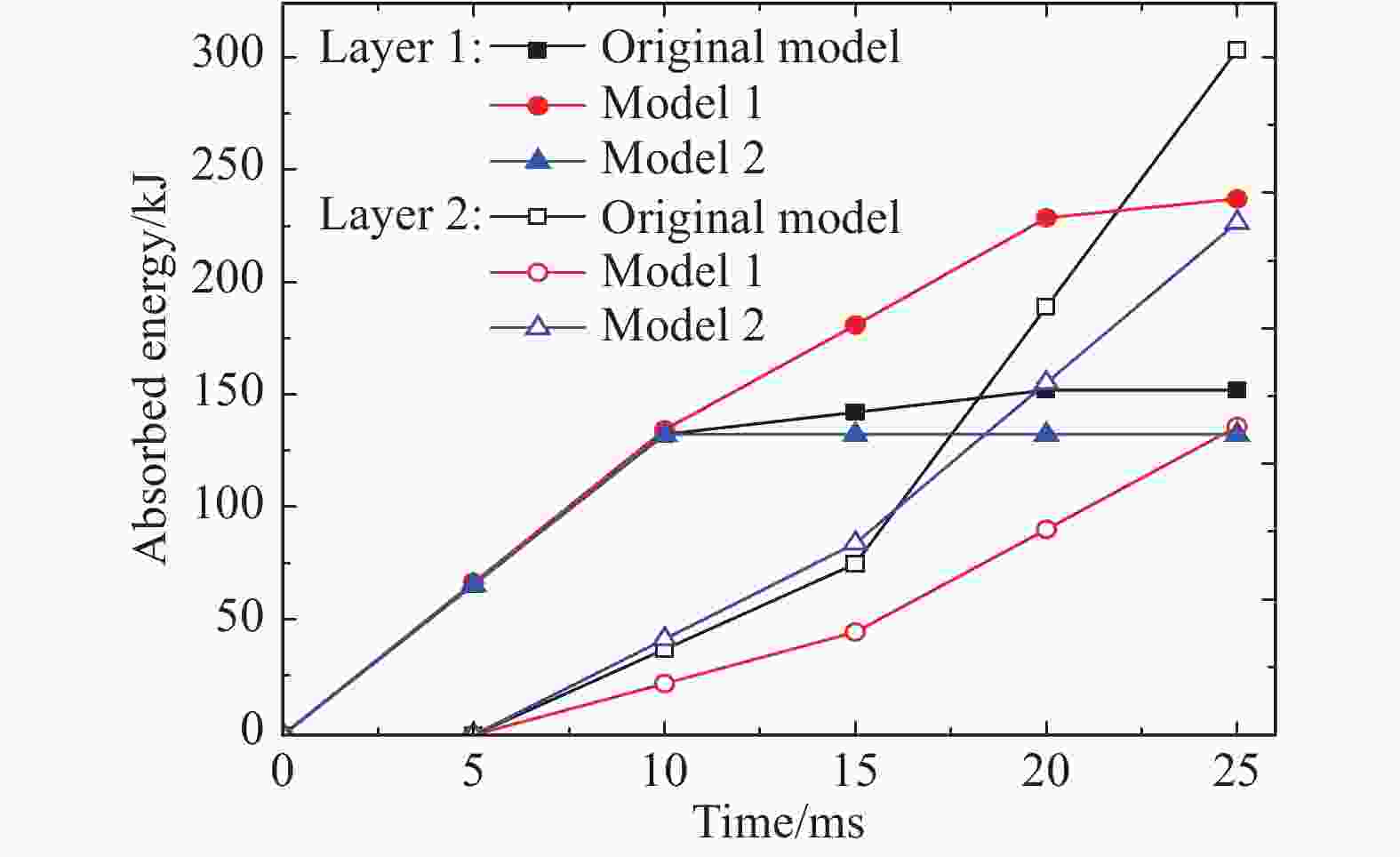
表 1 不同模型的平台应力设置和吸能量
Table 1. The setting of plateau stresses and the energy absorption of the models
模型 平台应力/MPa 吸收能量/kJ 吸能总量/
kJ吸能层1 吸能层2 吸能层1 吸能层2 原模型 150 100 150.9 299.6 450.5 对照模型1 130 100 234.5 134.9 369.4 对照模型2 150 80 131.5 224.2 355.7 -
[1] DRAZETIC P, TASSIN R, RAVALARD Y, et al. Experimentation and modelling of climbing phenomena of guided transport vehicles [J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit, 1995, 209(16): 11–17. doi: 10.1243/PIME_PROC_1995_209_249_02 [2] AMBRÓSIO J A C, PEREIRA M F O S, DIAS J P. Distributed and discrete nonlinear deformations on multibody dynamics [J]. Nonlinear Dynamics, 1996, 10(4): 359–379. doi: 10.1007/BF00045482 [3] HAN H S, KOO J S. Simulation of train crashes in three dimensions [J]. Vehicle System Dynamics, 2003, 40(6): 435–450. doi: 10.1076/vesd.40.6.435.17906 [4] FMILHO J, CAMBRÓSIO J A, SPEREIRA M F O. Validated multibody model for train crash analysis [J]. International Journal of Crashworthiness, 2003, 8(4): 339–352. doi: 10.1533/ijcr.2003.0242 [5] PEREIRA M, AMBROSIO J, DIAS J. Crashworthiness analysis and design using rigid-flexible multibody dynamics with application to train vehicles [J]. International Journal for Numerical Methods in Engineering, 1997, 40(4): 655–687. doi: 10.1002/(SICI)1097-0207(19970228)40:4<655:AID-NME84>3.0.CO;2-N [6] DIAS J P, PEREIRA M S. Optimization methods for crashworthiness design using multibody models [J]. Computers & Structures, 2004, 82(17-19): 1371–1380. doi: 10.1016/S0045-7949(04)00122-1 [7] DUAN L, SUN G, CUI J, et al. Crashworthiness design of vehicle structure with tailor rolled blank [J]. Structural & Multidisciplinary Optimization, 2016, 53(2): 321–338. doi: 10.1007/s00158-015-1315-z [8] TYRELL D, PERLMAN A B. Evaluation of rail passenger equipment crashworthiness strategies [J]. Transportation Research Record Journal of the Transportation Research Board, 2003, 1825(1): 8–14. doi: 10.3141/1825-02 [9] WKIRKPATRICK S, MSCHROEDER, SIMONS J W. Evaluation of passenger rail vehicle crashworthiness [J]. International Journal of Crashworthiness, 2001, 6(1): 95–106. doi: 10.1533/cras.2001.0165 [10] SIMONS J W, KIRKPATRICK S W. High-speed passenger train crashworthiness and occupant survivability [J]. International Journal of Crashworthiness, 2012, 4(2): 121–132. doi: 10.1533/cras.1999.0095 [11] BELINGARDI G, CAVATORTA M P, DUELLA R. Material characterization of a composite–foam sandwich for the front structure of a high speed train [J]. Composite Structures, 2003, 61(1/2): 13–25. doi: 10.1016/S0263-8223(03)00028-X [12] HU D, WANG Y, SONG B, et al. Energy absorption characteristics of a foam-filled tri-tube under axial quasi-static loading: experiment and numerical simulation [J]. International Journal of Crashworthiness, 2017: 1–16. doi: 10.1080/13588265.2017.1331494 [13] 李松晏, 郑志军, 虞吉林. 高速列车吸能结构设计和耐撞性分析 [J]. 爆炸与冲击, 2015, 35(2): 164–170 doi: 10.11883/1001-1455(2015)02-0164-07LI Songyan, ZHENG Zhijun, YU Jilin. Energy-absorbing structure design and crashworthiness analysis of high-speed trains [J]. Explosion and Shock Waves, 2015, 35(2): 164–170 doi: 10.11883/1001-1455(2015)02-0164-07 [14] REID S R, PENG C. Dynamic uniaxial crushing of wood [J]. International Journal of Impact Engineering, 1997, 19(5/6): 531–570. doi: 10.1016/S0734-743X(97)00016-X [15] ZHENG Z J, LIU Y D, YU J L, et al. Dynamic crushing of cellular materials: continuum-based wave models for the transitional and shock modes [J]. International Journal of Impact Engineering, 2012, 42: 66–79. doi: 10.1016/j.ijimpeng.2011.09.009 -






 下载:
下载: