A theoretical method for the calculation of flow field behind blast reflected waves
-
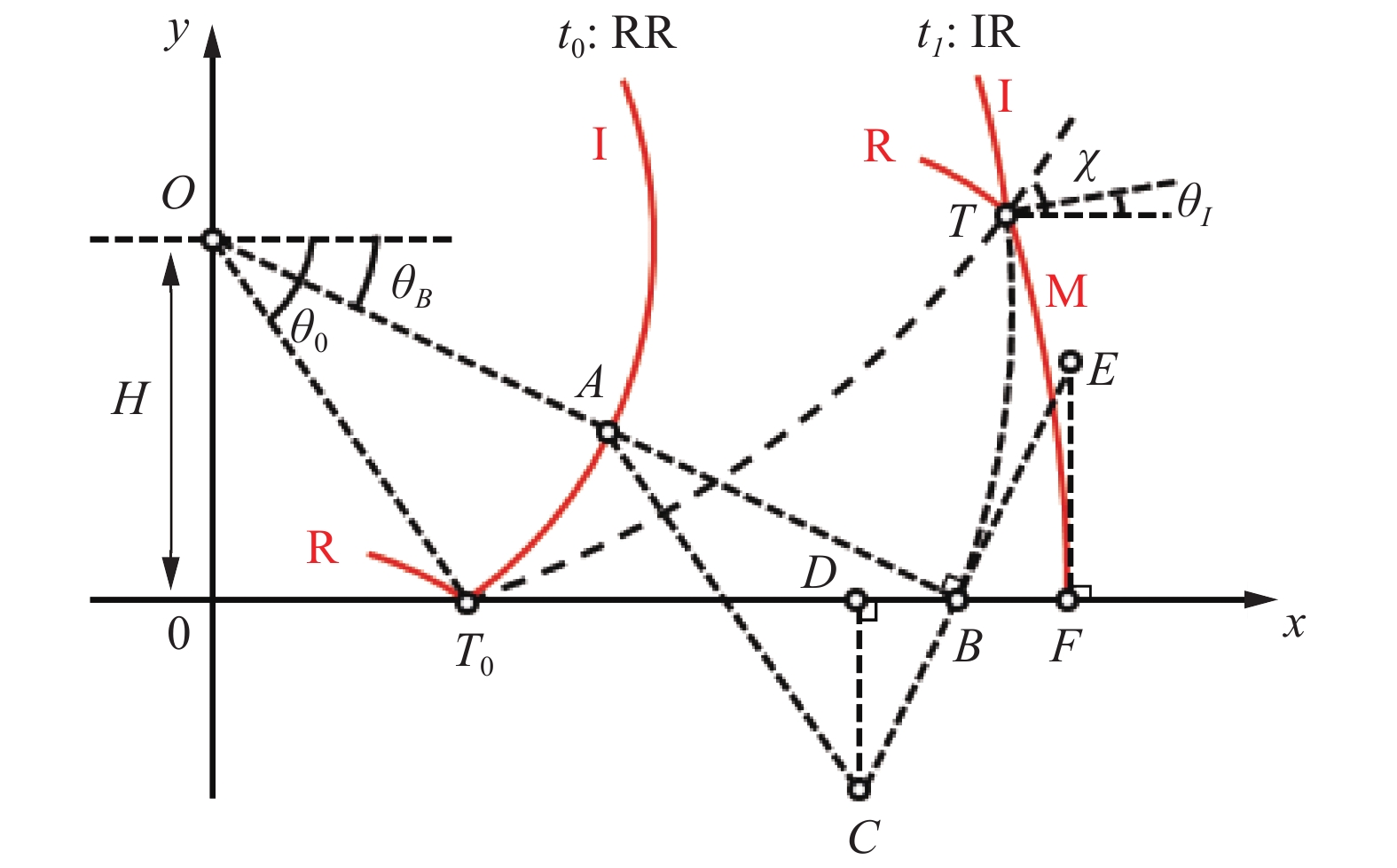
摘要: 爆炸冲击波遇到固壁,依次发生正规和非正规反射。本文中基于镜像方法,将爆炸冲击波在固壁反射等效为真实和虚拟爆炸流场的相互作用,建立了波后流场的理论计算方法。首先,假定反射波是以虚拟爆源为中心的圆弧,马赫杆是以爆心在固壁投影点为中心的圆弧。然后,根据爆炸自由场传播规律,利用基于几何近似的方法,建立流场中冲击波结构随时间演化的计算方法,确定任意时刻波后流场区域。最后,利用新发展的叠加模型LAMBR (LAMB revisied),将真实和虚拟爆炸流场进行叠加,给出波后流场中的压力、密度和速度等物理量。通过与数值模拟结果和已有数据进行对比,发现该方法得到的流场物理量分布、峰值等能够反映流场发展的主要规律,从而验证了该理论方法的合理性。而且,该理论方法所需的时间相较于数值模拟大大缩短。Abstract: Upon impinging on a rigid surface, the blast wave would go through regular and irregular reflection successively. A theoretical model is developed for the determination of the flow field behind the reflected wave, which is based on the method of image and identifies the field around blast wave reflection with that resulting from the interaction of real and imaginary bursts. Firstly, approximations of both reflected wave and Mach stems to circular arcs, centered on the imaginary burst point and ground zero respectively, are made. Then, given the blast free field, the method based on geometrical similarity is applied to calculate the temporal evolution of shock wave structures and differentiate different flow zones. Lastly, a newly developed addition model LAMBR (LAMB revisied) is employed to obtain the field parameters behind the reflected wave. The field parameter contours and peak values are in good agreement with the numerical results and the data from UFC 3-340-02, so the theoretical model is valid. And, the time needed for the theoretical calculation is much shorter than that for numerical simulation.
-
Key words:
- blast wave /
- irregular reflection /
- method of image /
- theoretical calculation
-
表 1 不同比例爆高条件下g 的取值
Table 1. The value of g at different scaled heights of explosion
$\bar H$/(m·kg−1/3) ${\bar x_{{{T,1}}}}$/(m·kg−1/3) ${\bar x_{{{T,2}}}}$/(m·kg−1/3) gUFC gYi 0.396 7 0.793 4 1.895 8 0.837 7 0.361 1 0.595 1 0.793 4 2.444 0 0.774 2 0.299 5 0.793 4 0.793 4 3.424 8 0.638 8 0.254 0 0.991 7 1.586 8 4.020 8 0.537 2 0.218 9 注: UFC 中数据采用英制单位,本文使用时换算为国际单位制。 表 2 非正规反射起始点坐标
${x_{{T_0}}}$ Table 2. The
${x_{{T_0}}}$ value of the starting point of IRH /m ${x_{{T_0}}}$/m 数值计算 理论分析 0.396 7 0.333 2 0.328 4 0.595 1 0.473 4 0.488 4 0.793 4 0.620 2 0.646 4 0.991 7 0.796 0 0.805 9 表 3 沿直线y=0.03 m的物理量峰值
Table 3. Peak values of parameters along the line y=0.03 m
t/s ps/(105 Pa) ρs/(kg·m−3) us/(m·s−1) NS TA ε/% NS TA1 ε1/% TA2 ε2/% NS TA1 ε1/% TA2 ε2/% 4.76×10−4 40.82 36.56 −10.44 7.81 7.86 0.64 6.54 −16.26 728.93 688.84 −5.50 513.35 −25.45 9.96×10−4 9.73 10.70 9.97 4.42 5.70 28.96 5.71 29.19 732.33 766.03 4.60 482.88 −34.06 1.92×10−3 4.46 4.41 −1.12 3.19 3.37 5.64 3.76 17.87 418.37 413.92 −1.06 342.21 −18.20 3.60×10−3 2.51 2.57 2.39 2.29 2.36 3.06 2.59 13.10 239.09 245.65 2.74 229.38 −4.07 注:NS 为数值结果,TA 为理论结果,ε=(TA-NS)/NS 为偏差。下标 1、2 分别表示基于 LAMBR 和 LAMB 模型的理论结果。 -
[1] KREHL P O K. History of shock waves, explosions and impact: a chronological and biographical reference[M]. Springer Science and Business Media, 2008: 1−9. [2] EHRHARDT L, BOUTILLIER J, MAGNAN P, et al. Evaluation of overpressure prediction models for air blast above the triple point [J]. Journal of Hazardous Materials, 2016, 311: 176–185. DOI: 10.1016/j.jhazmat.2016.02.051. [3] XU W Z, WU W G, LIN Y S. Numerical method and simplified analytical model for predicting the blast load in a partially confined chamber [J]. Computers and Mathematics with Applications, 2018, 76: 284–314. DOI: 10.1016/j.camwa.2018.04.019. [4] BEWICK B, FLOOD I, CHEN Z. A neural-network model-based engineering tool for blast wall protection of structures [J]. International Journal of Protective Structures, 2011, 2(2): 159–176. DOI: 10.1260/2041-4196.2.2.159. [5] ARMAGHANI D J, HASANIPANAH M, MAHDIYAR A, et al. Airblast prediction through a hybrid genetic algorithm: ANN model [J]. Neural Computing and Applications, 2018, 29(9): 619–629. DOI: 10.1007/s00521-016-2598-8. [6] CHAN P C, KLEIN H H. A study of blast effects inside an enclosure [J]. Journal of Fluids Engineering, 1994, 116(3): 450–455. DOI: 10.1115/1.2910297. [7] KONG Xiangshao, WU Weiguo, LI Jun, et al. Experimental investigation on characteristics of blast load in partially confined cabin structure [J]. Journal of Shanghai Jiaotong University (Science), 2013, 18(5): 583–589. DOI: 10.1007/s12204-013-1431-0. [8] KONG B, LEE K, LEE S, et al. Indoor propagation and assessment of blast waves from weapons using the alternative image theory [J]. Shock Waves, 2016, 26: 75–85. DOI: 10.1007/s00193-015-0581-4. [9] WU Z, GUO J, YAO X, et al. Analysis of explosion in enclosure based on improved method of images [J]. Shock Waves, 2017, 27(2): 237–245. DOI: 10.1007/s00193-016-0655-y. [10] KANDULA M, FREEMAN R. On the interaction and coalescence of spherical blast waves [J]. Shock Waves, 2008, 18: 21–33. DOI: 10.1007/s00193-008-0134-1. [11] 马涛. 空气中爆炸波快速算法研究[D]. 长沙: 国防科学技术大学, 2014: 6−16MA Tao. The study for fast computation of blast wave in air [D]. Changsha: National University of Defense Technology, 2014: 6−16. [12] NEEDHAM C E. Blast waves [M]. New York: Springer, 2010. [13] DOD U S. Structures to resist the effects of accidental explosions: UFC 3-340-02 [R]. USA: Department of Defense, 2008. [14] BEN-DOR G. Shock wave reflection phenomena [M]. New York: Springer, 2007: 25−36. [15] 易仰贤. 空爆冲击波马赫反射近似计算 [J]. 爆炸与冲击, 1983, 3(2): 44–49. DOI: 10.11883/1001-1455(1983)02-044-06.YI Yangxian. Approximate calculation of Mach reflection of explosive shock waves in air [J]. Explosion and Shock Waves, 1983, 3(2): 44–49. DOI: 10.11883/1001-1455(1983)02-044-06. [16] HU T C J, GLASS I I. Blast wave reflection trajectories from a height of burst [J]. AIAA Journal, 1986, 24(4): 607–610. DOI: 10.2514/3.9314. [17] 徐彬, 张寒虹, 陈志坚, 等. 球面激波在固壁的马赫反射: Ⅱ [J]. 爆炸与冲击, 1988, 8(1): 25–28. DOI: 10.11883/1001-1455(1988)01-0025-04.XU Bin, ZHANG Hanhong, CHEN Zhijian, et al. Mach reflection of spherical shock wave on rigid wall: Ⅱ [J]. Explosion and Shock Waves, 1988, 8(1): 25–28. DOI: 10.11883/1001-1455(1988)01-0025-04. [18] WANG Li. Mach stem height in pseudo-steady and unsteady Mach reflection [J]. Journal of Fudan University (Natural Science), 2010, 49(4): 513–519. DOI: 10.3788/HPLPB20102206.1351. [19] 王力, 韩峰, 陈放, 等. 偏心对称起爆战斗部破片初速的增益 [J]. 爆炸与冲击, 2016, 36(1): 69–74. DOI: 10.11883/1001-1455(2016)01-0069-06.WANG Li, HAN Feng, CHEN Fang, et al. Fragments’ velocity of eccentric warhead with double symmetric detonators [J]. Explosion and Shock Waves, 2016, 36(1): 69–74. DOI: 10.11883/1001-1455(2016)01-0069-06. [20] WHITHAM G B. A new approach to problems of shock dynamics: part I: two-dimensional problems [J]. Journal of Fluid Mechanics, 1957, 2(2): 145–171. DOI: 10.1017/S002211205700004X. [21] ITOH S, OKAZAKI N, ITAYA M. On the transition between regular and Mach reflection in truly non-stationary flows [J]. Journal of Fluid Mechanics, 1981, 108: 383–400. DOI: 10.1017/S0022112081002176. [22] SHIN J, WHITTAKER A S, CORMIE D. Incident and normally reflected overpressure and impulse for detonations of spherical high explosive in free air [J]. Journal of Structural Engineering, 2015, 141(12): 04015057. DOI: 10.1061/(ASCE)ST.1943-541X.0001305. -







 下载:
下载: