Components and attenuation of seismic wavesinduced by horizontal smooth blasting
-
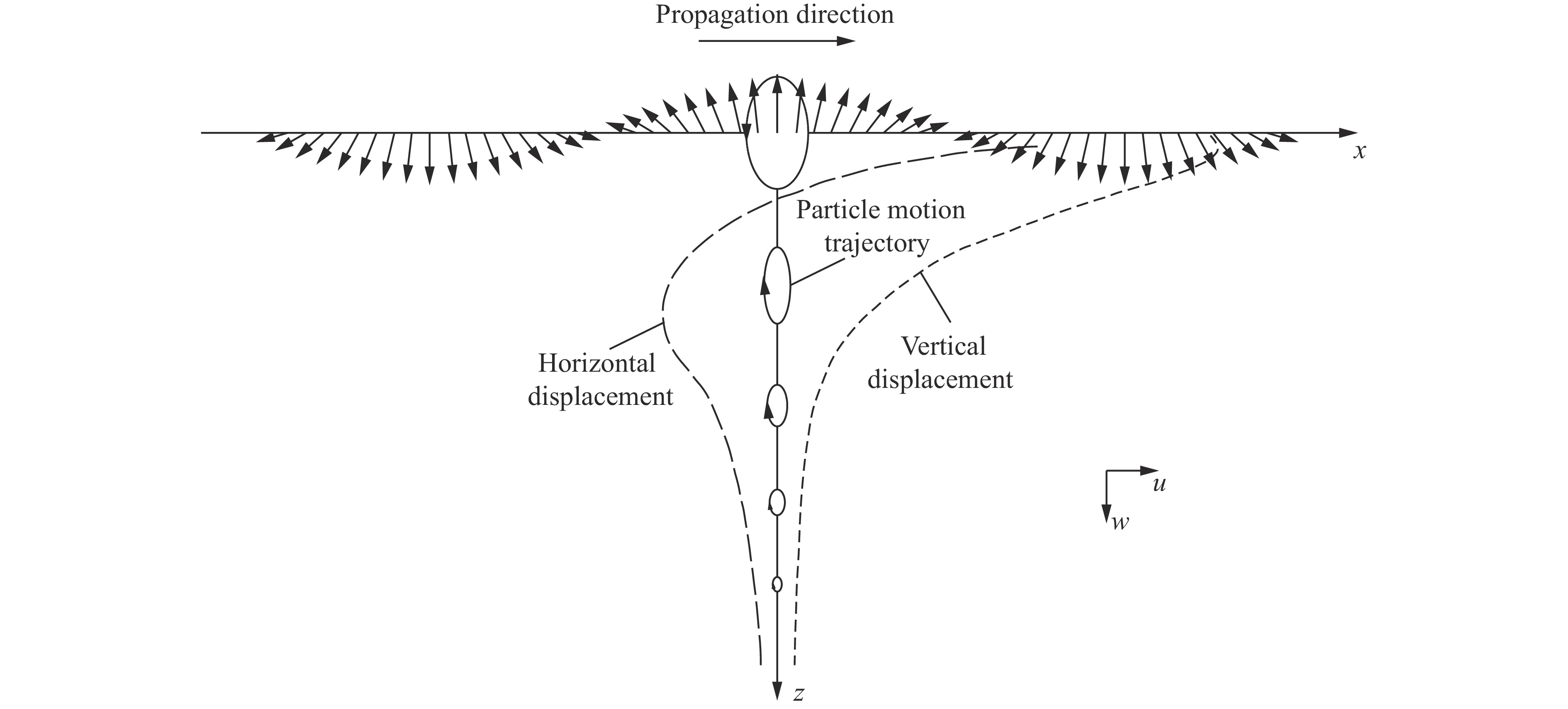
摘要: 借助极化偏振分析方法,针对一组现场爆破实验,分析了水平光面爆破激发地震波的成分构成及特性,比较了不同波的衰减特征及各自对爆破振动的影响,并探讨了水平光面爆破的内在力学机理。结果表明,爆破振动中不同波的相对量值及主导波的类型均会随测点位置的改变而变化,爆源特性和沿传播路径的不同衰减共同决定波的成分构成及演化,各测点的优势振动方向也与波的成分构成密切相关。对于水平光面爆破,在光爆孔平面上,P波的影响可忽略,S波主要在竖直向振动,R波对水平及竖直向的振动均有贡献,其中水平向的振动主要由R波引起,而S波的竖直向振速在近区远高于R波,但归因于S和R波的不同衰减,R波在距离爆源22.5 m/kg1/2(58~67 m)处开始主导竖直向的振动;在光爆孔平面外,P波的影响不可忽略,且在特定位置会成为优势波型。Abstract: In this paper, using polarization analysis, we characterized the seismic waves induced by the horizontal smooth blasting in a group of onsite blasting experiments, presenting interpretation of wave components and offering comparison of attenuation characteristics and evaluation of the influences of different waves. We also examined the inherent mechanical mechanism of the horizontal smooth blasting under some simplifications. The results show that the proportion of different waves and the dominant wave type both vary with the relative location of interest, and the dominant motion direction at a specific position closely correlates with the wave components. The pattern of the blasting source and the different attenuation characteristics jointly determine the wave components and their evolutions. For the horizontal smooth blasting, only S and R waves are included on the same plane of smooth blastholes, while the P wave component is negligible. The horizontal vibration is mainly caused by the R wave, while the S wave mainly vibrates in the vertical direction and its vertical velocity in the near field is much higher than that of the R wave. However, the R wave still dominates the vertical vibration if the scaled distance exceeds 22.5 m/kg1/2 (58−67 m), due to the different attenuation speeds of S and R waves. As for the seismic waves outside the same plane of smooth blastholes, the influence of the P wave cannot be ignored and it might become the dominant wave type somewhere. This study can help to enhance the understanding of blast-induced seismic waves.
-
表 1 各段的爆破药量和测点距离
Table 1. Charge weight and distance of each blast
测点 水平距离/m Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ #1 10.9 12.7 14.8 17.2 19.6 22.0 24.4 27.4 #2 15.9 17.7 19.8 22.2 24.6 27.0 29.4 32.4 #3 20.9 22.7 24.8 27.2 29.6 32.0 34.4 37.4 #4 18.3 16.5 14.4 12.0 9.6 7.2 4.8 1.8 药量/kg 6.6 6.6 7.7 7.7 8.8 8.8 8.8 13.2 -
[1] 卢文波, 赖世骧, 朱传云, 等. 三峡工程岩石基础开挖爆破震动控制安全标准 [J]. 爆炸与冲击, 2001, 21(1): 67–71. doi: 10.3321/j.issn:1001-1455.2001.01.014LU Wenbo, LAI Shixiang, ZHU Chuanyun, et al. Safety standards of blast vibrations adopted in rock base excavation of the Three Gorge Project [J]. Explosion and Shock Waves, 2001, 21(1): 67–71. doi: 10.3321/j.issn:1001-1455.2001.01.014 [2] 李海波, 蒋会军, 赵坚, 等. 动荷载作用下岩体工程安全的几个问题 [J]. 岩石力学与工程学报, 2003, 22(11): 1887–1891. doi: 10.3321/j.issn:1000-6915.2003.11.028LI Haibo, JIANG Huijun, ZHAO Jian, et al. Some problems about safety analysis of rock engineering under dynamic load [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1887–1891. doi: 10.3321/j.issn:1000-6915.2003.11.028 [3] 卢文波, 李海波, 陈明, 等. 水电工程爆破振动安全判据及应用中的几个关键问题 [J]. 岩石力学与工程学报, 2009, 28(8): 1513–1520. doi: 10.3321/j.issn:1000-6915.2009.08.001LU Wenbo, LI Haibo, CHEN Ming, et al. Safety criteria of blasting vibration in hydropower engineering and several key problems in their application [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1513–1520. doi: 10.3321/j.issn:1000-6915.2009.08.001 [4] MCGARR A. Estimating ground motions for small nearby earthquakes [C] // Seismic Design of Embankments and Caverns. New York: ASCE, 1983: 113−127. [5] 吕涛, 石永强, 黄诚, 等. 非线性回归法求解爆破振动速度衰减公式参数 [J]. 岩土力学, 2007, 28(9): 1871–1878. doi: 10.3969/j.issn.1000-7598.2007.09.019LYU Tao, SHI Yongqiang, HUANG Cheng, et al. Study on attenuation parameters of blasting vibration by nonlinear regression analysis [J]. Rock and Soil Mechanics, 2007, 28(9): 1871–1878. doi: 10.3969/j.issn.1000-7598.2007.09.019 [6] BLAIR D P. Non-linear superposition models of blast vibration [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 235–247. doi: 10.1016/j.ijrmms.2007.05.002 [7] 卢文波, HUSTRULID W. 质点峰值振动速度衰减公式的改进 [J]. 工程爆破, 2002, 8(3): 1–4. doi: 10.3969/j.issn.1006-7051.2002.03.001LU Wenbo, HUSTRULID W. An improvement to the equation for the attenuation of the peak particle velocity [J]. Engineering blasting, 2002, 8(3): 1–4. doi: 10.3969/j.issn.1006-7051.2002.03.001 [8] KHANDELWAL M, SINGH T N. Prediction of blast-induced ground vibration using artificial neural network [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(7): 1214–1222. doi: 10.1016/j.ijrmms.2009.03.004 [9] 施建俊, 李庆亚, 张琪, 等. 基于Matlab和BP神经网络的爆破振动预测系统 [J]. 爆炸与冲击, 2017, 37(6): 1087–1092. DOI: 10.11883/1001-1455(2017)06-1087-06.SHI Jianjun, LI Qingya, ZHANG Qi, et al. Forecast system for blasting vibration velocity peak based on Matlab and BP neural network [J]. Explosion and Shock Waves, 2017, 37(6): 1087–1092. DOI: 10.11883/1001-1455(2017)06-1087-06. [10] SINGH P K, ROY M P. Damage to surface structures due to blast vibration [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(6): 949–961. doi: 10.1016/j.ijrmms.2010.06.010 [11] 周俊汝, 卢文波, 张乐, 等. 爆破地震波传播过程的振动频率衰减规律研究 [J]. 岩石力学与工程学报, 2014, 33(11): 2171–2178.ZHOU Junru, LU Wenbo, ZHANG Le, et al. Attenuation of vibration frequency during propagation of blasting seismic wave [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2171–2178. [12] 杨建华, 姚池, 卢文波, 等. 深埋隧洞钻爆开挖围岩振动频率特性研究 [J]. 岩土力学, 2017, 38(4): 1195–1202.YANG Jianhua, YAO Chi, LU Wenbo, et al. Vibration frequency characteristics of surrounding rock of deep tunnel induced by borehole-blasting [J]. Rock and Soil Mechanics, 2017, 38(4): 1195–1202. [13] 武旭, 张云鹏, 郭奇峰. 台阶地形爆破振动放大与衰减效应研究 [J]. 爆炸与冲击, 2017, 37(6): 1017–1022. DOI: 10.11883/1001-1455(2017)06-1017-06.WU Xu, ZHANG Yunpeng, GUO Qifeng. Amplification and attenuation effect of blasting vibration on step topography [J]. Explosion and Shock Waves, 2017, 37(6): 1017–1022. DOI: 10.11883/1001-1455(2017)06-1017-06. [14] 钟冬望, 何理, 操鹏, 等. 基于精确毫秒延时控制的爆破降振试验研究 [J]. 煤炭学报, 2015, 40(S1): 107–112.ZHONG Dongwang, HE Li, CAO Peng, et al. Experimental study of reducing vibration intensity based on controlled blasting with precise time delay [J]. Journal of China Coal Society, 2015, 40(S1): 107–112. [15] 朱俊, 杨建华, 卢文波, 等. 地应力影响下隧洞边墙的爆破振动安全 [J]. 爆炸与冲击, 2014, 34(2): 153–160. DOI: 10.11883/1001-1455(2014)02-0153-08.ZHU Jun, YANG Jianhua, LU Wenbo, et al. Influences of blasting vibration on the sidewall of underground tunnel [J]. Explosion and Shock Waves, 2014, 34(2): 153–160. DOI: 10.11883/1001-1455(2014)02-0153-08. [16] 冷振东, 卢文波, 胡浩然, 等. 爆生自由面对边坡微差爆破诱发振动峰值的影响 [J]. 岩石力学与工程学报, 2016, 35(9): 1815–1822.LENG Zhendong, LU Wenbo, HU Haoran, et al. Studies on influence of blast-created free face on ground vibration in slope blasts with millisecond-delays [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(9): 1815–1822. [17] 高启栋, 卢文波, 冷振东, 等. 隧洞开挖过程中掏槽孔起爆位置的优选 [J]. 振动与冲击, 2018, 37(9): 8–16.GAO Qidong, LU Wenbo, LENG Zhendong, et al. Optimization of cut-hole detonator position in tunnel excavation [J]. Journal of Vibration and Control, 2018, 37(9): 8–16. [18] DOWDING C H. Construction vibrations [M]. NJ: Prentice Hall, 1996. [19] FAVREAU R F. Generation of strain waves in rock by an explosion in a spherical cavity [J]. Journal of Geophysical Research, 1969, 74(17): 4267–4280. doi: 10.1029/JB074i017p04267 [20] GRAFF K F. Wave motion in elastic solid [M]. Oxford University Press, 1975. [21] HEELAN P A. Radiation from a cylindrical source of finite length [J]. Geophysics, 1953, 18(3): 685. doi: 10.1190/1.1437923 [22] BLAIR D P. Seismic radiation from an explosive column [J]. Geophysics, 2010, 75(1): 55–65. [23] FRÉDÉRIC V, ENRIQUE P C, LUIS A Q. P and S Mach waves generated by the detonation of a cylindrical explosive charge: experiments and simulations [J]. Fragblast, 2002, 6(1): 21–35. doi: 10.1076/frag.6.1.21.8849 [24] AKI K, RICHARDS P G. Quantitative Seismology [M]. 2nd ed. Sausalito, California: University Science Books, 2002. [25] 阿肯巴赫. 弹性固体中波的传播 [M]. 上海: 同济大学出版社, 1992. [26] 王礼立. 应力波基础 [M]. 北京: 国防工业出版社, 2005. [27] GAO Qidong, LU Wenbo, HU Yingguo, et al. An evaluation of numerical approaches for S-wave component simulation in rock blasting [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(5): 830–842. doi: 10.1016/j.jrmge.2017.05.004 [28] 金旭浩, 卢文波, 田勇, 等. 岩石爆破过程S波的产生机制分析 [J]. 岩土力学, 2011(S2): 228–232.JIN Xuhao, LU Wenbo, TIAN Yong, et al. Analysis of mechanisms of S wave generated in rock blasting process [J]. Rock and Soil Mechanics, 2011(S2): 228–232. [29] 胡英国, 卢文波, 高启栋, 等. 不同爆破模拟方法下S波产生机制的比较 [J]. 爆破, 2015, 32(3): 10–16. doi: 10.3963/j.issn.1001-487X.2015.03.002HU Yingguo, LU Wenbo, GAO Qidong, et al. Comparison of generation of S-wave with different simulation approach [J]. Blasting, 2015, 32(3): 10–16. doi: 10.3963/j.issn.1001-487X.2015.03.002 [30] 杨招伟, 卢文波, 高启栋, 等. 爆破地震波中S波识别方法及其应用 [J]. 爆炸与冲击, 2018, 38(1): 28–36. DOI: 10.11883/bzycj-2017-0178.YANG Zhaowei, LU Wenbo, GAO Qidong, et al. A S-wave phase picking method for blasting seismic waves and its application in engineering [J]. Explosion and Shock Waves, 2018, 38(1): 28–36. DOI: 10.11883/bzycj-2017-0178. [31] KUZMENKO A A, VOROBEV V D, DENISYUK I I, et al. Seismic effects of blasting in rock [M]. 1993: 16−22. [32] FOTI S, LAI C, RIX G, et al. Surface wave methods for near-surface characterization [M]. Boca Raton, FL, Crossref: CRC Press, 2014. [33] 郑治真, 朱传镇, 胡祚春. 爆破与地震的差异 [J]. 地球物理学报, 1975, 18(3): 208–216.ZHENG Zhizhen, ZHU Chuanzhen, HU Zuochun. Differences between explosions and earthquakes [J]. Chinese journal of geophysics, 1975, 18(3): 208–216. -







 下载:
下载: