空中强爆炸冲击波地面反射规律数值模拟研究

姚成宝; 王宏亮; 浦锡锋; 寿列枫; 王智环

doi:10.11883/bzycj-2018-0287

空中强爆炸冲击波地面反射规律数值模拟研究

doi: 10.11883/bzycj-2018-0287

1.
北京大学数学科学学院，北京 100871
2.
西北核技术研究院，陕西西安 710024

基金项目: 国家自然科学基金(11421101，11325102)

详细信息

作者简介:
姚成宝（1984－　），男，博士，助理研究员，yaocheng@pku.edu.cn

中图分类号: O383
计量
- 文章访问数: 5323
- HTML全文浏览量: 2353
- PDF下载量: 123
- 被引次数: 0
出版历程
- 收稿日期: 2018-08-08
- 修回日期: 2018-11-01
- 刊出日期: 2019-11-01

Numerical simulation of intense blast wave reflected on rigid ground

1.
School of Mathematical Sciences, Peking University, Beijing 100871, China
2.
Northwest Institute of Nuclear Technology, Xi’an 710024, Shaanxi, China

摘要

摘要: 为准确预测空中强爆炸产生的冲击波载荷分布，基于欧拉坐标系建立了能够模拟具有高密度比、高压力比的强激波问题的二维多介质流体数值方法。结合网格自适应技术，对1 kt TNT当量的空中强爆炸在不同爆炸高度下的冲击波地面反射过程进行了数值模拟，并考虑了真实气体状态方程和空气随高度不均匀分布的影响。计算得到了地面上距爆心投影点大尺度范围内的反射超压和冲量等冲击波载荷分布，并给出了冲击波载荷随爆高的变化规律。
- 空中强爆炸 /
- 多介质流体 /
- 网格自适应 /
- 冲击波反射 /
- 爆高
Abstract: In order to predict the intense blast wave in air, a multi-material numerical scheme is proposed in two-dimensional cylindrical coordinates on Eulerian grids, which can handle the blast wave problems with high ratio in initial density and pressure. Combined with the adaptive mesh technique, the propagation of blast wave produced by a 1 kt TNT intense explosion is simulated, and the effects of real gas equation of state and the nonuniform atmosphere are taken into account. The calculated blast wave parameters on the ground, such as peak overpressures and impulses, agree well with the experimental data in a wide space range, and the influences of heights of burst are analyzed.
- air blast /
- multi-material flow /
- mesh adaption /
- shock reflection /
- height of burst

HTML全文

图 1 不同参考密度下真实气体状态方程的热力学参数关系

Figure 1. Plots of equations of state for real gas at different reference densities

下载: 全尺寸图片幻灯片

图 2 多介质流体计算模型示意图

Figure 2. Schematic diagram for the multi-media fluid calculation model

下载: 全尺寸图片幻灯片

图 3 典型时刻的冲击波压力等值线图和网格自适应图

Figure 3. Pressure contours and adaptive meshes at typical times

下载: 全尺寸图片幻灯片

图 4 地面不同距离处的冲击波峰值超压和冲量

Figure 4. Peak overpressures and impulses at different radii

下载: 全尺寸图片幻灯片

图 5 不同爆高下的地面冲击波峰值超压和冲量

Figure 5. Peak overpressures and impulses at different heights of burst

下载: 全尺寸图片幻灯片

参考文献(23)

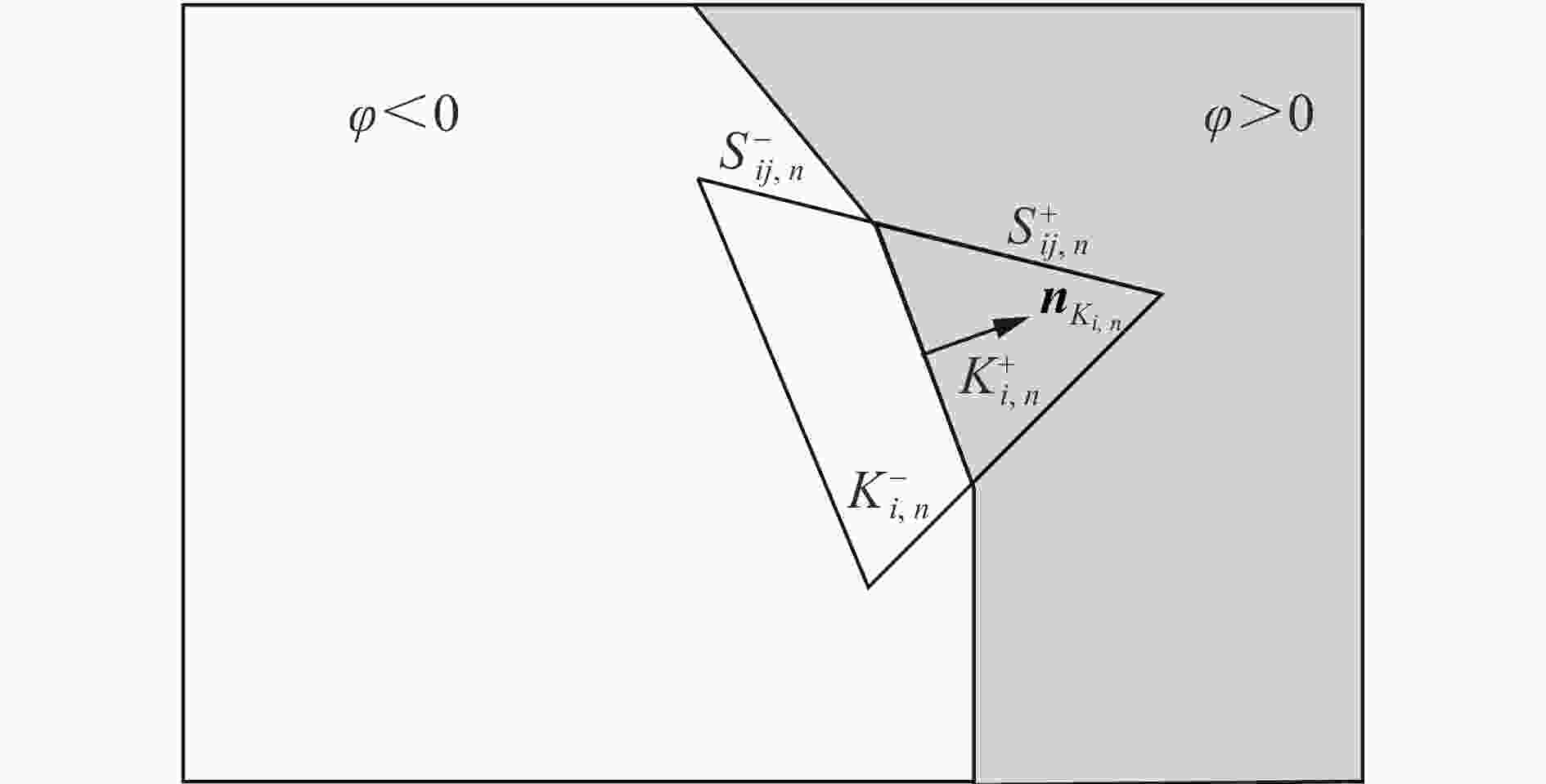
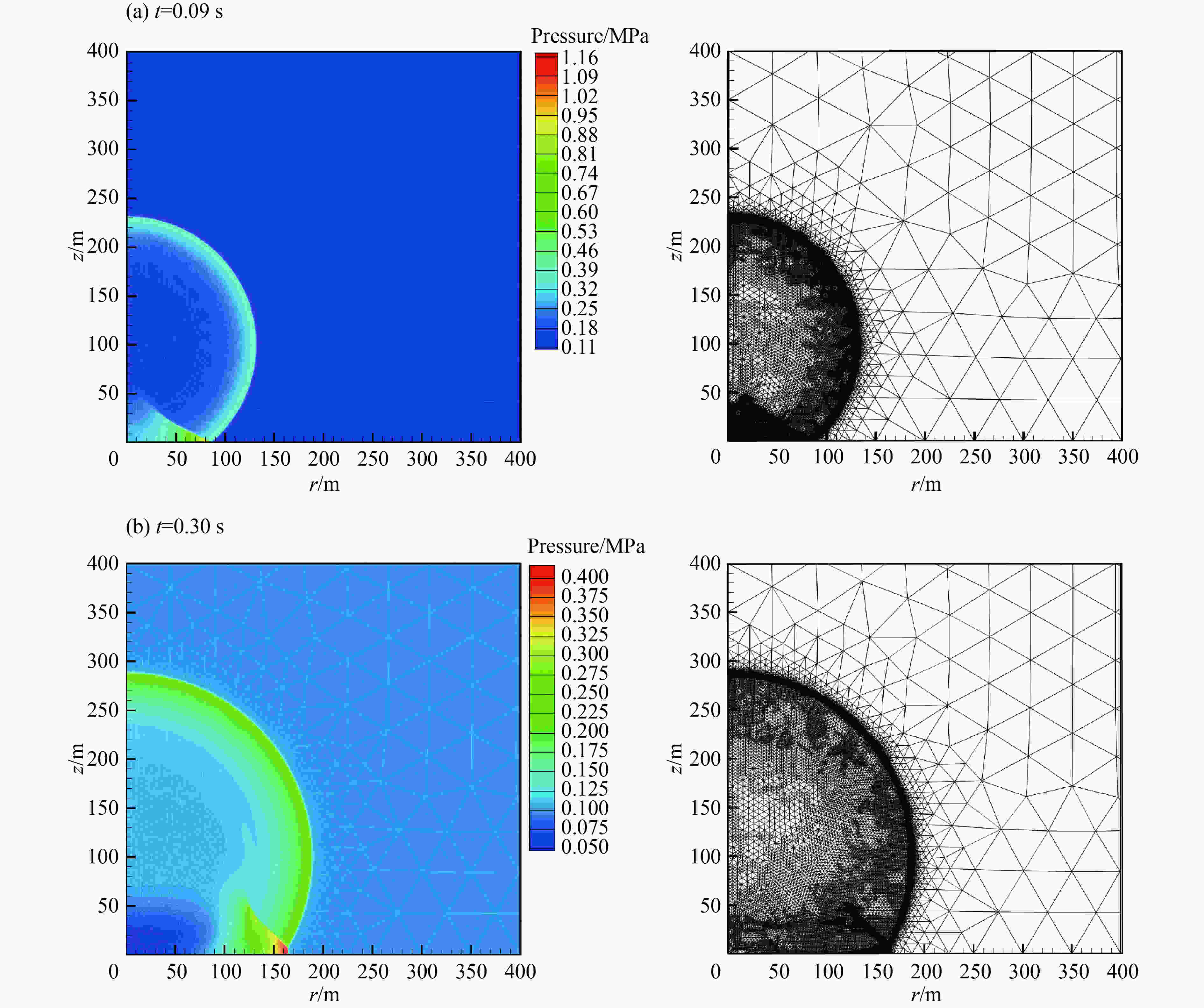
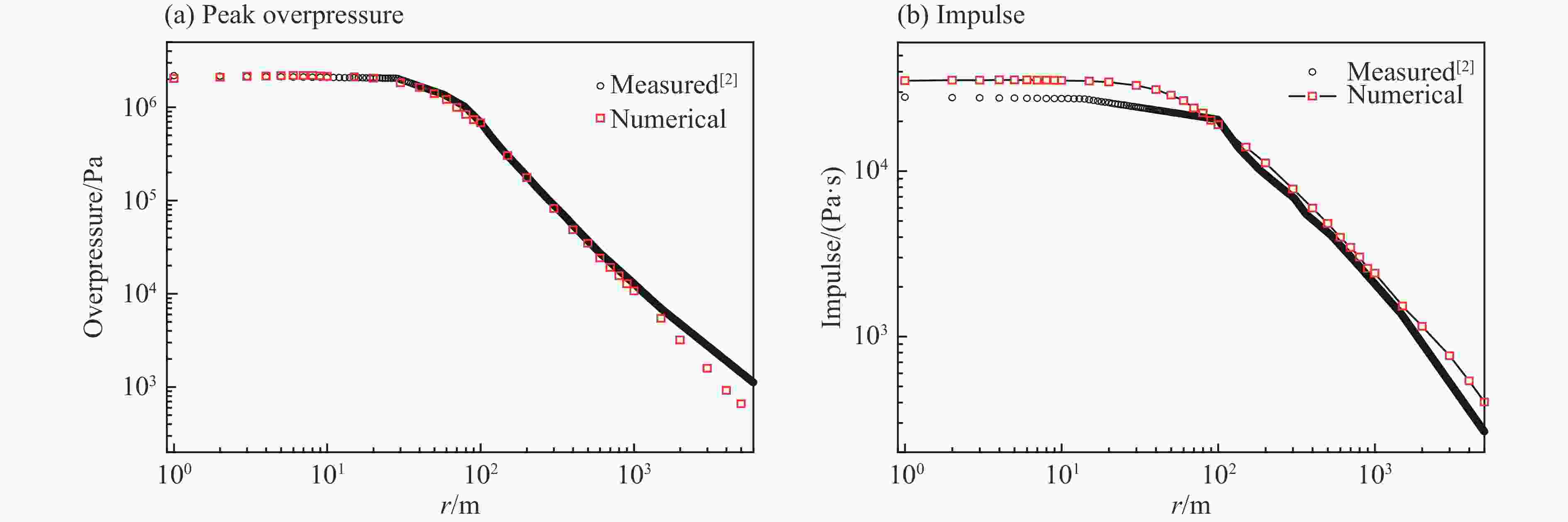
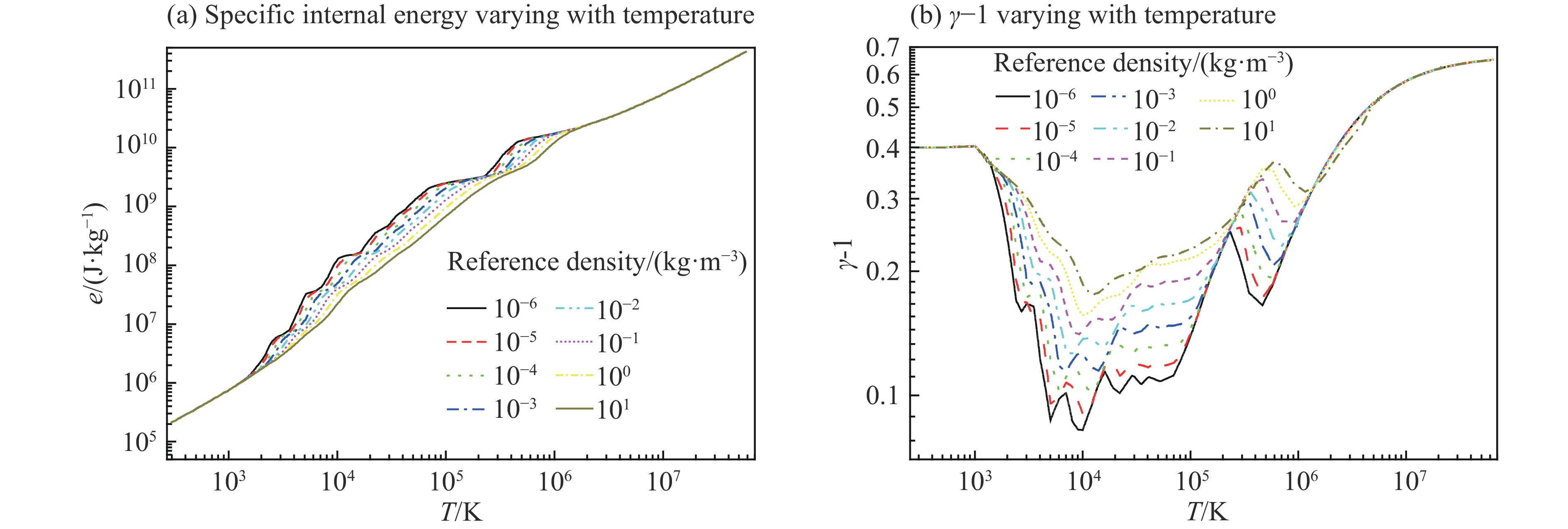
[1]	乔登江. 核爆炸物理概论[M]. 北京: 国防工业出版社, 2003: 51−55.
[2]	GLASSTONE S, DOLAN P J. The effects of nuclear weapons [R]. USA: Defense Technical Information Center, 1977: 453−501. DOI: 10.21236/ada087568.
[3]	段晓瑜, 崔庆忠, 郭学永, 等. 炸药在空气中爆炸冲击波的地面反射超压实验研究 [J]. 兵工学报, 2016, 37(12): 2277–2283. DOI: 10.3969/j.issn.1000-1093.2016.12.013. DUAN Xiaoyu, CUI Qingzhong, GUO Xueyong, et al. Experimental investigation of ground reflected overpressure of shock wave in air blast [J]. Acta Armamentarii, 2016, 37(12): 2277–2283. DOI: 10.3969/j.issn.1000-1093.2016.12.013.
[4]	HIRT C W, AMSDEN A A, COOK J L. An arbitrary Lagrangian-Eulerian computing method for all flow speeds [J]. Journal of Computational Physics, 1974, 14(3): 227–253. DOI: 10.1016/0021-9991(74)90051-5.
[5]	OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations [J]. Journal of Computational Physics, 1988, 79(1): 12–49. DOI: 10.1016/0021-9991(88)90002-2.
[6]	TRYGGVASON G, BUNNER B, ESMAEELI A, et al. A front-tracking method for the computations of multiphase flow [J]. Journal of Computational Physics, 2001, 169(2): 708–759. DOI: 10.1006/jcph.2001.6726.
[7]	FEDKIW R P, ASLAM T, MERRIMAN B, et al. A non-oscillatory Eulerian approach to interfaces in multimaterial flows: the ghost fluid method [J]. Journal of Computational Physics, 1999, 152(2): 457–492. DOI: 10.1006/jcph.1999.6236.
[8]	LIU T G, KHOO B C, WANG C W. The ghost fluid method for compressible gas-water simulation [J]. Journal of Computational Physics, 2005, 204(1): 193–221. DOI: 10.1016/j.jcp.2004.10.012.
[9]	SCHOCH S, NORDIN-BATES K, NIKIFORAKIS N. An Eulerian algorithm for coupled simulations of elastoplastic-solids and condensed-phase explosives [J]. Journal of Computational Physics, 2013, 252: 163–194. DOI: 10.1016/j.jcp.2013.06.020.
[10]	CROWL W K. Structures to resist the effects of accidental explosions [M]. USA: US Army, Navy and Air Force, US Government Printing Office, 1969: 205−315.
[11]	徐维铮, 吴卫国. 爆炸波高精度数值计算程序开发及应用 [J]. 中国舰船研究, 2017, 12(3): 64–74. DOI: 10.3969/j.issn.1673-3185.2017.03.010. XU Weizheng, WU Weiguo. Development of in-house high-resolution hydrocode for assessment of blast waves and its application [J]. Chinese Journal of Ship Research, 2017, 12(3): 64–74. DOI: 10.3969/j.issn.1673-3185.2017.03.010.
[12]	TÜRKER L. Thermobaric and enhanced blast explosives (TBX and EBX) [J]. Defence Technology, 2016, 12(6): 423–445. DOI: 10.1016/j.dt.2016.09.002.
[13]	张洪武, 何扬, 张昌权. 空中爆炸冲击波地面荷载的数值模拟 [J]. 爆炸与冲击, 1992, 12(2): 156–165. ZHANG Hongwu, HE Yang, ZHANG Changquan. Numerical simulation on ground surface loading of shock wave from air explosions [J]. Explosion and Shock Waves, 1992, 12(2): 156–165.
[14]	赵海涛, 王成. 空中爆炸问题的高精度数值模拟研究 [J]. 兵工学报, 2013, 34(12): 1536–1546. DOI: 10.3969/j.issn.1000-1093.2013.12.008. ZHAO Haitao, WANG Cheng. High resolution numerical simulation of air explosion [J]. Acta Armamentarii, 2013, 34(12): 1536–1546. DOI: 10.3969/j.issn.1000-1093.2013.12.008.
[15]	BAKER W E. Explosions in air [M]. USA: University of Texas Press, 1973: 55−95.
[16]	姚成宝, 李若, 田宙, 等. 空气自由场中强爆炸冲击波传播二维数值模拟 [J]. 爆炸与冲击, 2015, 35(4): 585–590. DOI: 10.11883/1001-1455(2015)04-0585-06. YAO Chengbao, LI Ruo, TIAN Zhou, et al. Two dimensional simulation for shock wave produced by strong explosion in free air [J]. Explosion and Shock Waves, 2015, 35(4): 585–590. DOI: 10.11883/1001-1455(2015)04-0585-06.
[17]	姚成宝, 浦锡锋, 寿列枫, 等. 强爆炸冲击波在不均匀空气中传播数值模拟 [J]. 计算力学学报, 2015, 32(S1): 6–9. YAO Chengbao, PU Xifeng, SHOU Liefeng, et al. Numeircal simulation of blast wave propagation in nonuniform air [J]. Chinese Journal of Computational Mechanics, 2015, 32(S1): 6–9.
[18]	SYMBALISTY E M D, ZINN J, WHITAKER R W. RADFLO physics and algorithms: LA-12988-MS [R]. USA: Los Alamos National Lab, 1995. DOI: 10.2172/110714.
[19]	SETHIAN J A. Evolution, implementation, and application of level set and fast marching methods for advancing fronts [J]. Journal of Computational Physics, 2001, 169(2): 503–555. DOI: 10.1006/jcph.2000.6657.
[20]	SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow [J]. Journal of Computational Physics, 1994, 114(1): 146–159. DOI: 10.1006/jcph.1994.1155.
[21]	DI Yana, LI Ruo, TANG Tao, et al. Level set calculations for incompressible two-phase flows on a dynamically adaptive grid [J]. Journal of Scientific Computing, 2007, 31(1/2): 75–98. DOI: 1007/s10915-006-9119-3.
[22]	TORO E F. Riemann solvers and numerical methods for fluid dynamics [M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2009: 102-200. DOI: 10.1007/b79761.
[23]	LI R, WU S N. h-adaptive mesh method with double tolerance adaptive strategy for hyperbolic conservation laws [J]. Journal of Scientific Computing, 2013, 56(3): 616–636. DOI: 10.1007/s10915-013-9692-1.