Millisecond time for reducing vibration between two holes for slope blasting determined by stability coefficient of time history
-
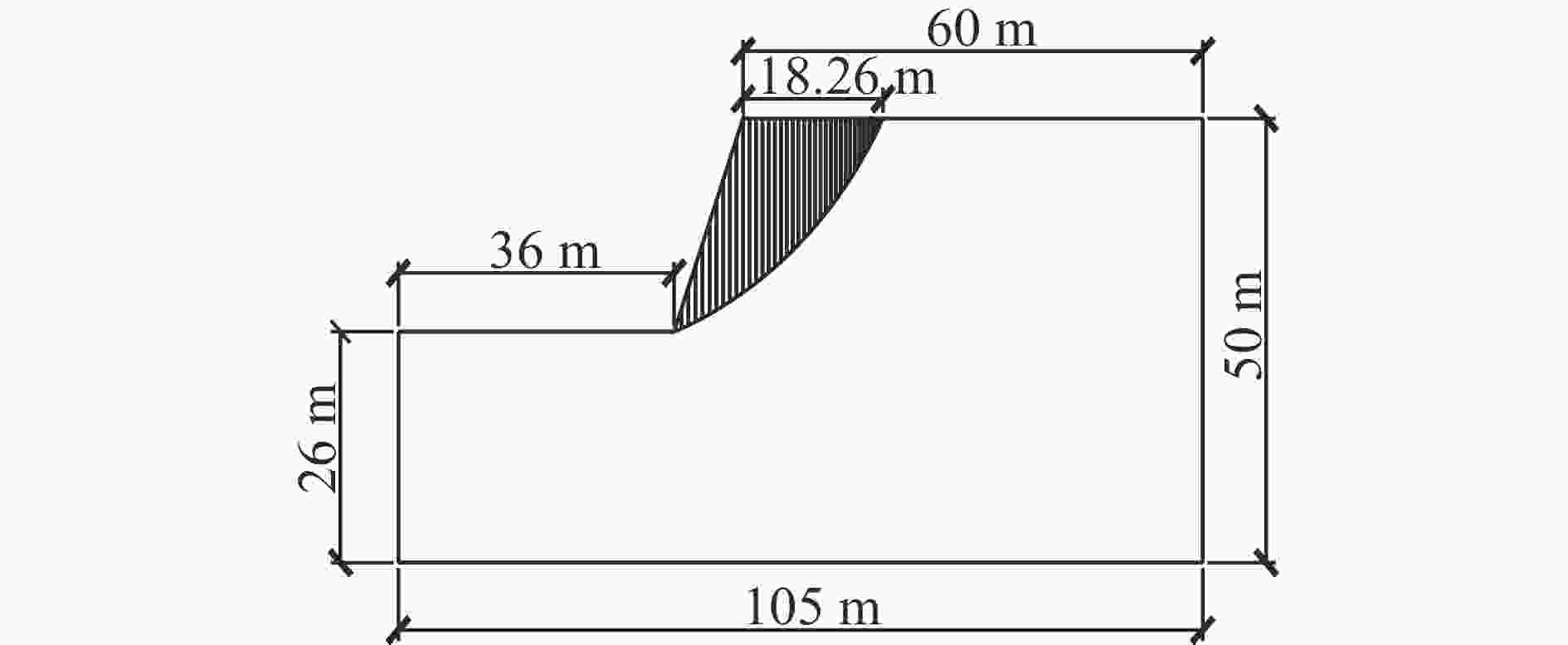
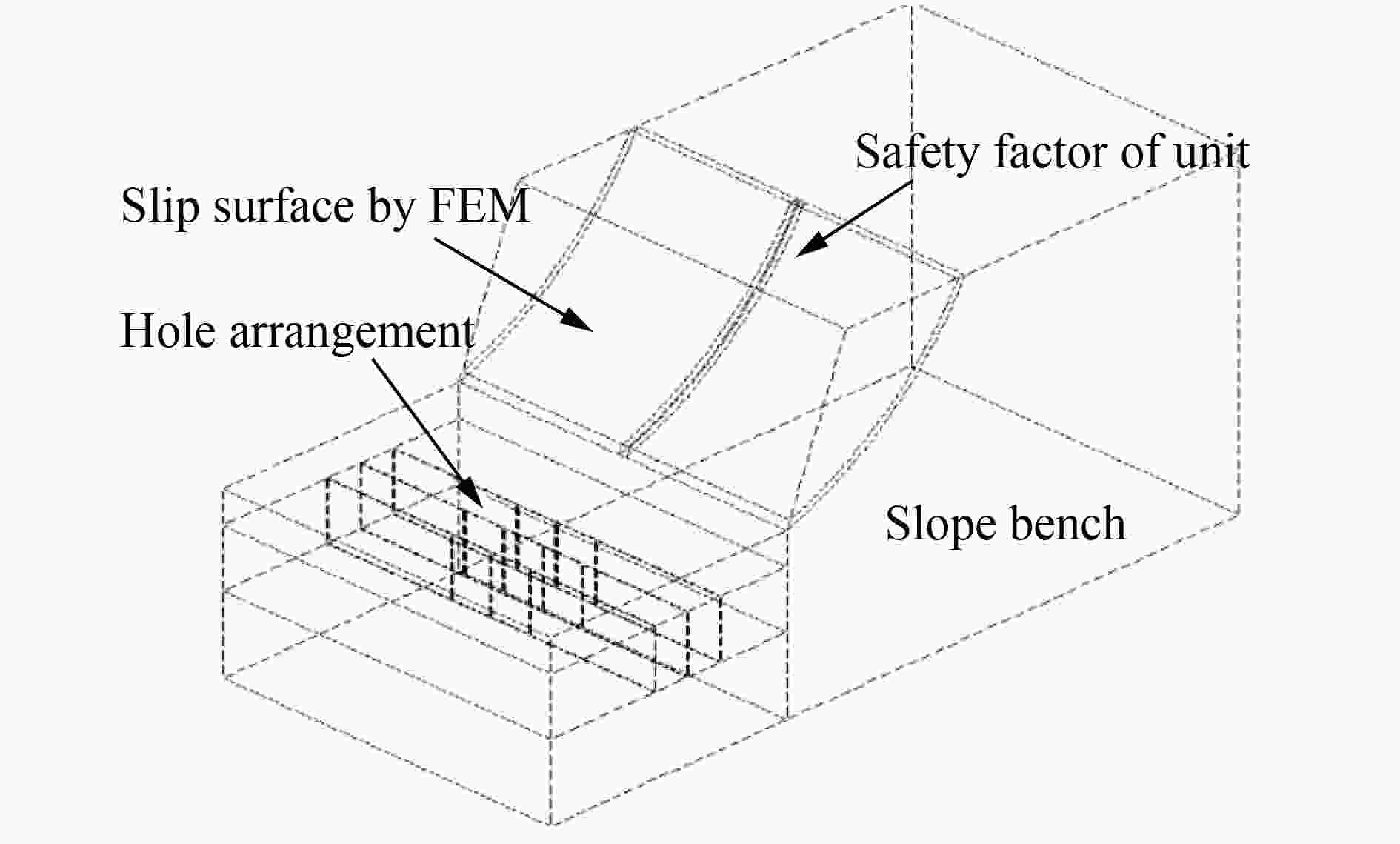
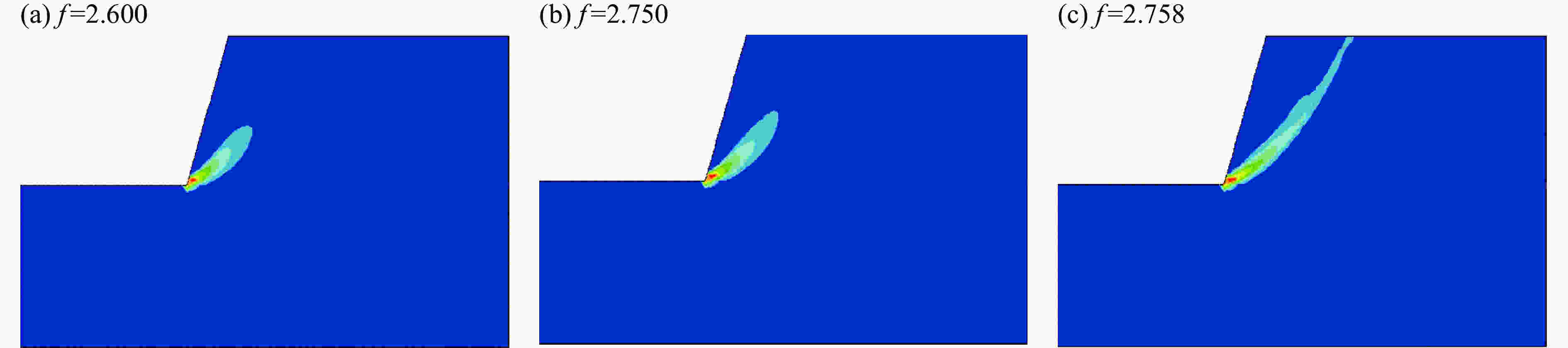
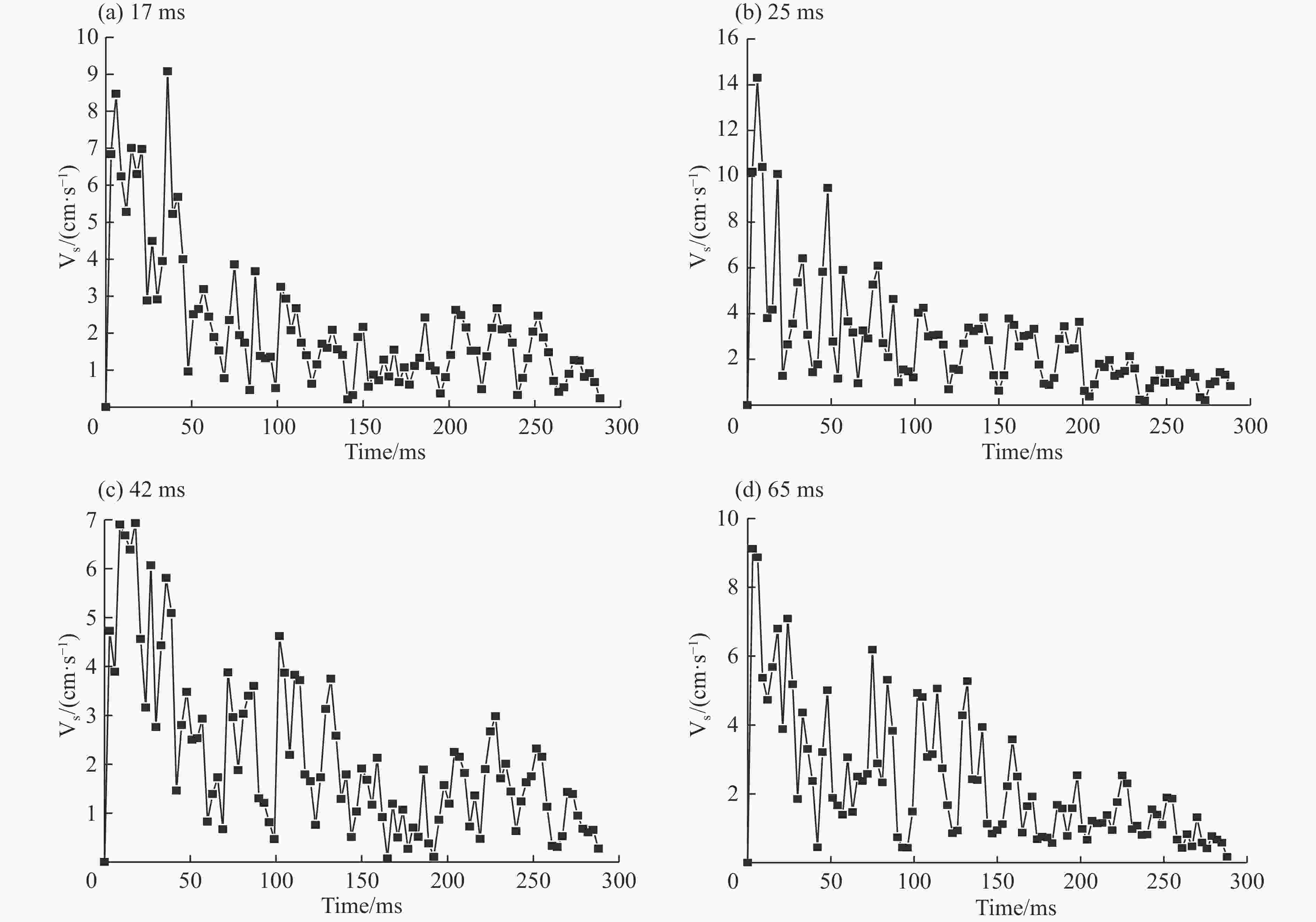
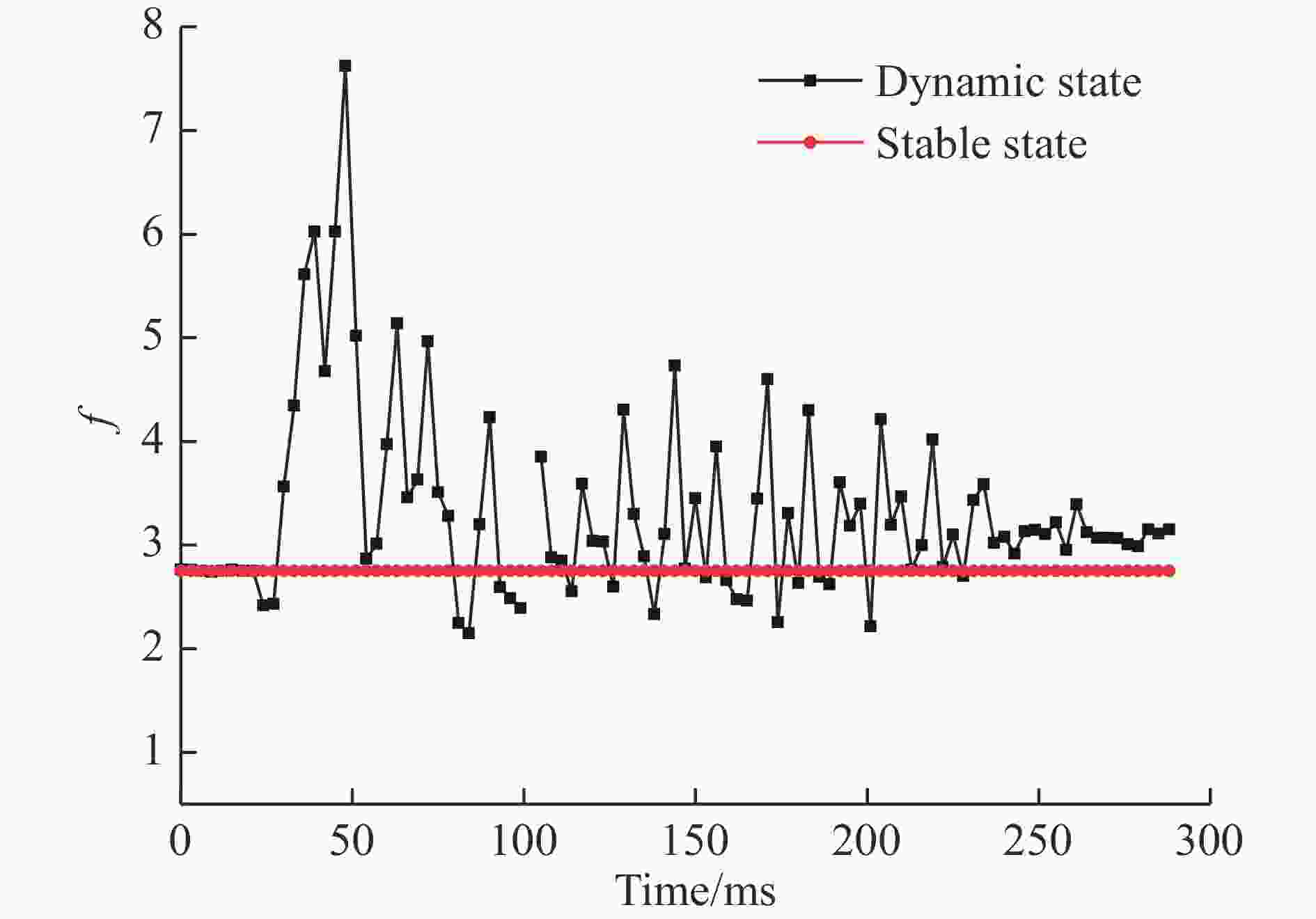
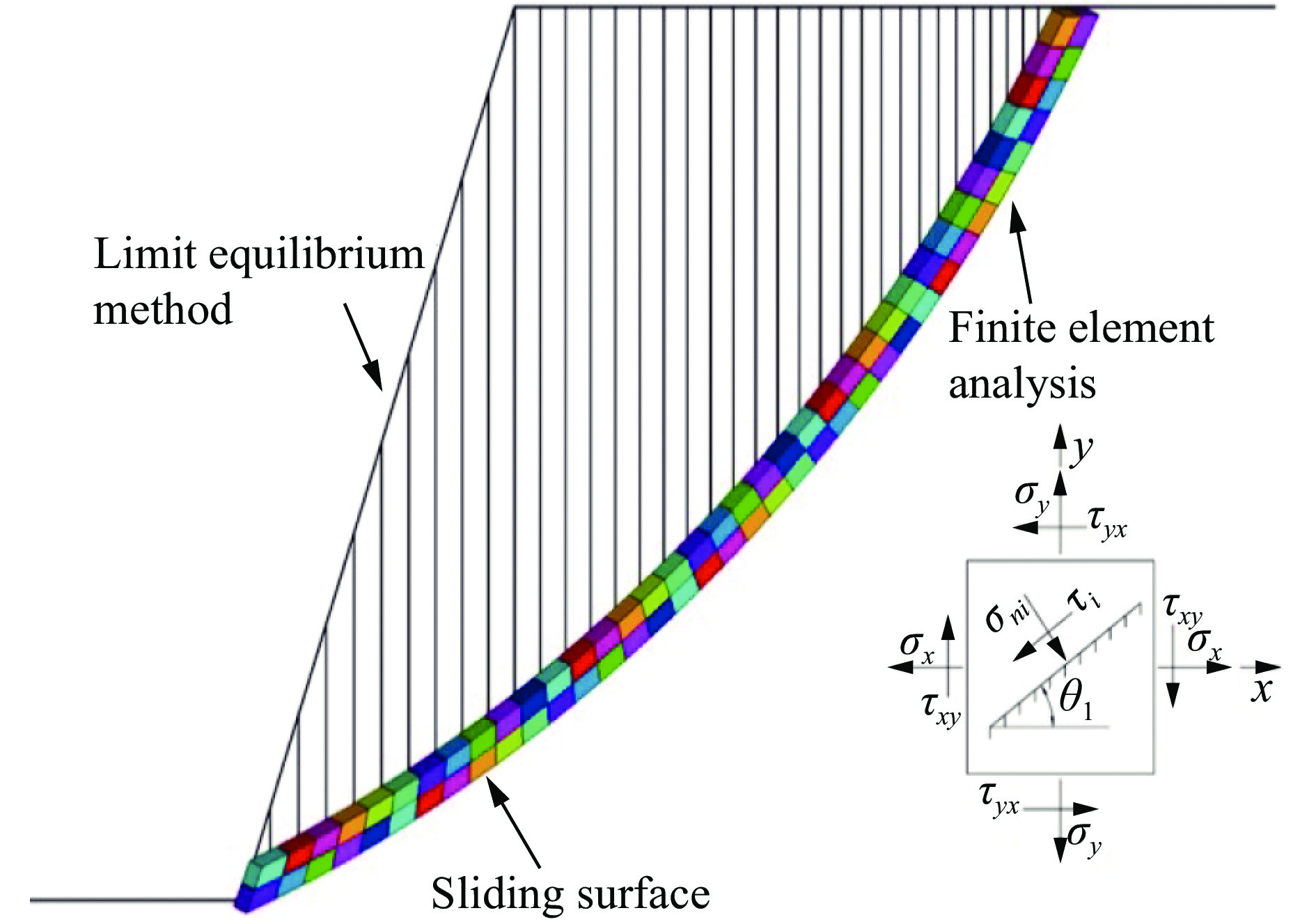
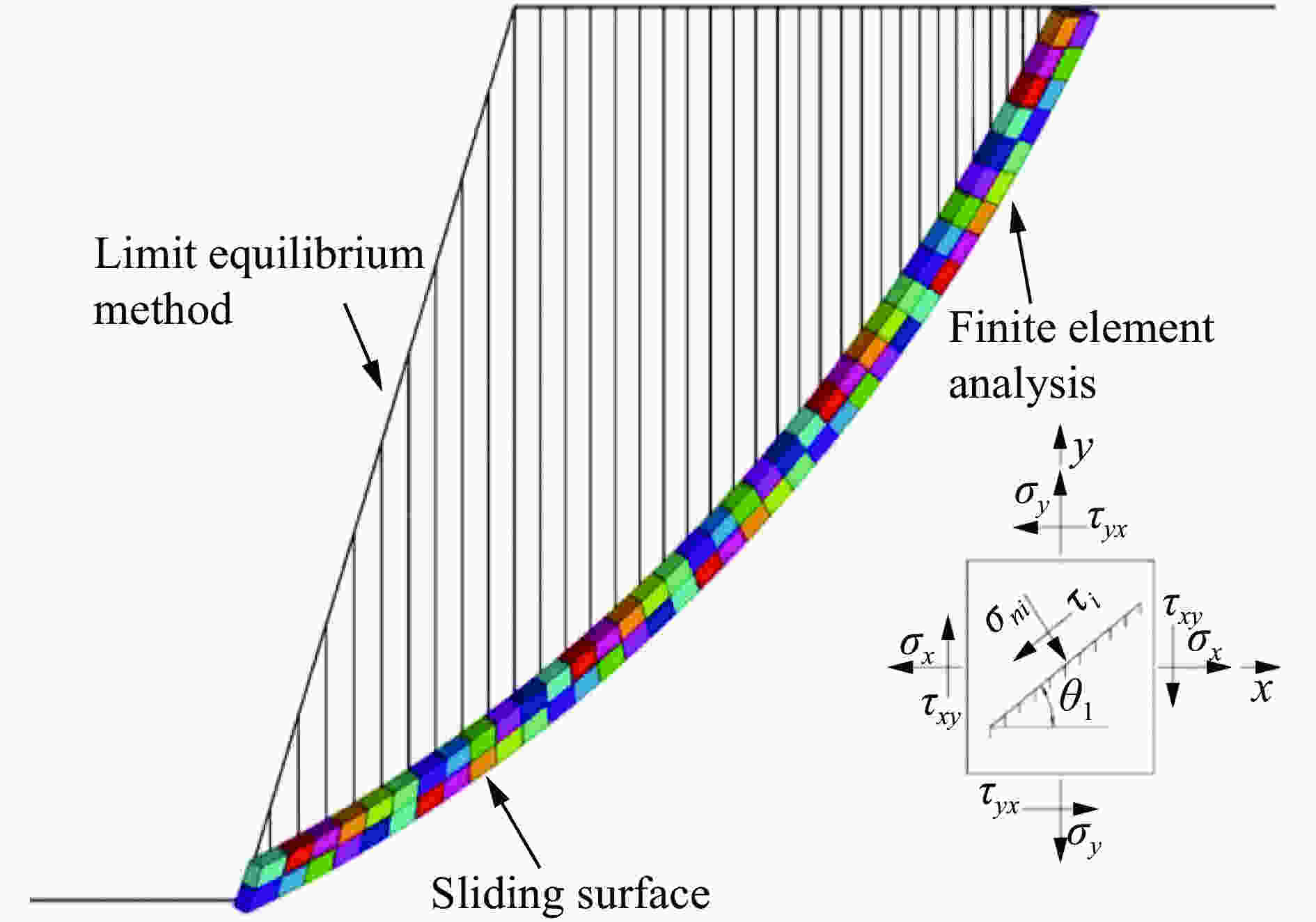
摘要: 为了获得边坡逐孔爆破最佳降振微差时间,以某个实际边坡逐孔微差爆破施工现场为原型,先利用ANSYS建立二维静态模型,借助有限元折减法确定自然状态下的潜在滑动面和静态安全系数;基于已确定的二维潜在滑动面重新建立同尺寸同性质的三维逐孔微差爆破动态模型,利用LS-DYAN进行动力分析,整个过程分别设置同排3个炮孔0、17、25、42和65 ms等5种不同孔间微差起爆方式;同时,对该施工现场进行排、孔间(25 ms,17 ms)、(25 ms,25 ms)、(25 ms,42 ms)、(25 ms,65 ms)等4种微差时间控制的等比例相似小炮测振实验。提取模拟结果中3个炮孔同时起爆时滑面单元的应力数值代入极限平衡法计算公式,绘制了冲击载荷作用下边坡稳定性系数曲线,通过对曲线的理论分析发现,最佳降振微差时间约为48 ms;而三维数值模拟和测振实验结果均显示,孔间微差时间取42 ms时降振效果较佳。这说明,边坡稳定性系数曲线给出的微差时间与模拟和实验结果较为接近,可为今后边坡逐孔微差爆破降振研究提供参考。Abstract: In the present study we found out about the optimum millisecond time for reducing vibration in hole-by-hole blasting, on the basis of an actual slope detonation work. At first we constructed a two-dimensional static model using ANSYS and determined the potential sliding surface and the static safety factor in the natural state using finite element reduction. Then we rebuilt the three-dimensional dynamic model of millisecond hole-by-hole blasting and carried out the dynamic analysis using LS-DYAN. In the whole process, we set up three holes in the same row using millisecond detonating by five differential millisecond time control of 0, 17, 25, 42 and 65 ms. At the end of the construction site, we conducted small-scale vibration tests of four millisecond time control in row holes (25 ms, 17 ms), (25 ms, 25 ms), (25 ms, 42 ms), (25 ms, 65 ms), with the stress value of the sliding surface unit during the simultaneous detonation of three holes in the simulated results taken into the formula of limit equilibrium, and drew out the time history curve of slope stability coefficient under impact loading. Analyzing the time history curve, we found that the optimum millisecond time for vibration reduction was 48 ms. Moreover, the results of three-dimensional numerical simulation and vibration test showed that the effect of vibration reduction was better when the millisecond time between holes was 42 ms. The result shows that the millisecond time, given by the slope stability coefficient, is consistent with the simulated and experimental results, which provides a reference for related research on vibration reduction of millisecond hole-by-hole blasting.
-
Key words:
- impact load /
- millisecond delay time /
- slope stability /
- safety factor /
- time history analysis
-
表 1 折减算法
Table 1. Strength reduction method
材料 凝聚力/kPa tanφ 内摩擦角φ/(°) 安全系数 状态 MAT1 220 0.358 7 20.550 1 收敛 MAT2 110 0.179 3 10.275 2 收敛 $ \vdots$ $ \vdots$ $ \vdots$ $ \vdots$ $ \vdots$ $ \vdots$ MAT8 80.0 0.130 4 7.473 2.75 收敛(塑性已经贯通) MAT9 7.91 0.129 0 7.392 2.78 不收敛 表 2 各种计算方式的安全系数
Table 2. Safety factor for each calculation method
计算方法 安全系数分析方法 安全系数 极限平衡法 Circle slip method 2.525 Bishop 2.505 Janbu 2.679 有限元法 Strength reduction FEM(2D) 2.750 Dynamic FEM(3D and t=0) 2.610 表 3 不同孔间微差时间下监测点峰值速度
Table 3. Monitoring point’s peak speed at different hole millisecond time
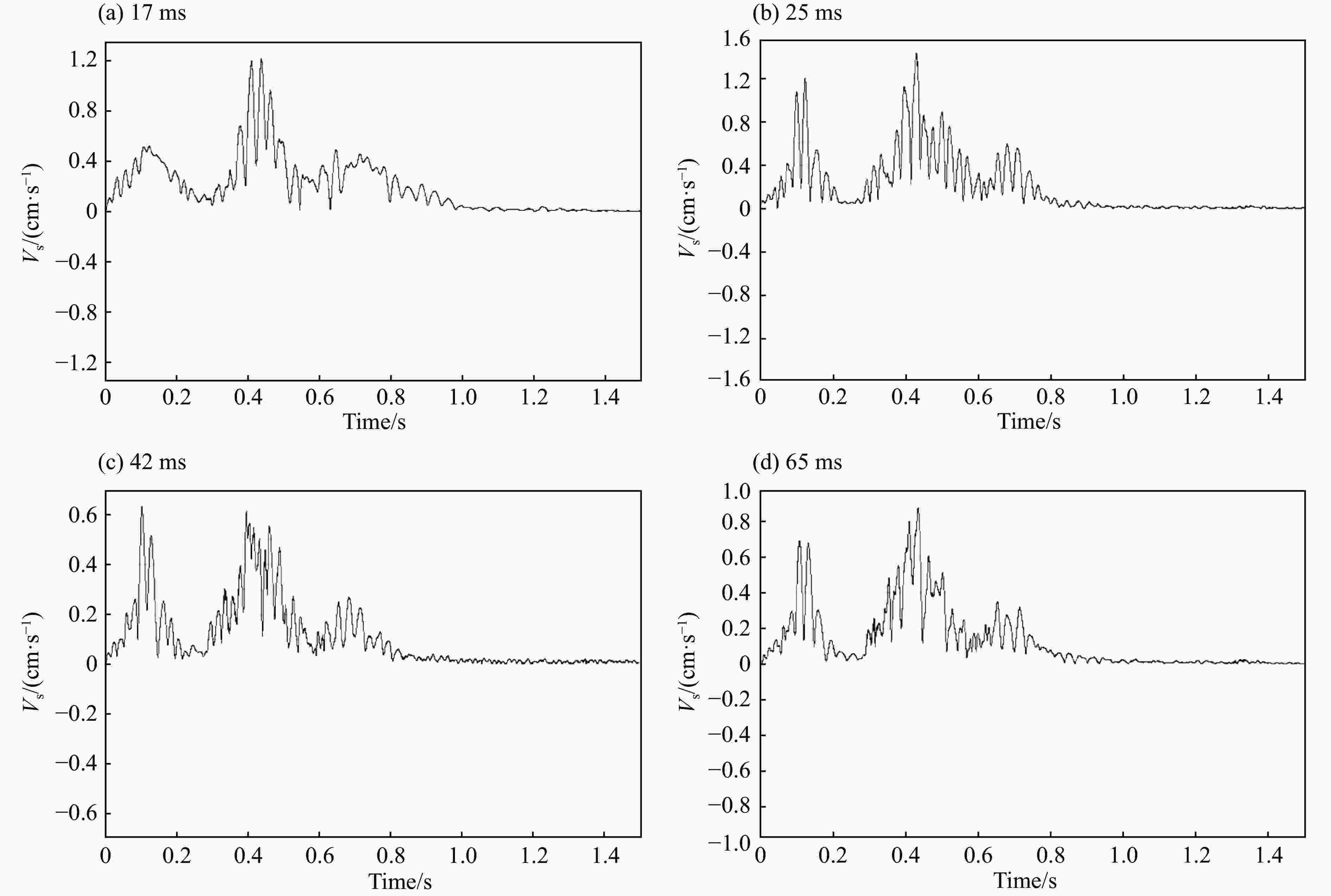
不同微差爆组 测点 Vx/(cm·s−1) Vy/(cm·s−1) Vz/(cm·s−1) Vs/(cm·s−1) (25 ms, 17 ms) A 0.736 1 0.483 6 1.158 9 1.222 7 B 0.719 4 0.421 1 1.203 1 1.067 7 C 0.669 8 0.502 3 1.149 9 1.138 1 D 0.750 2 0.469 1 1.210 1 1.294 1 (25 ms, 25 ms) A 1.115 0 1.286 1 0.475 4 1.436 1 B 1.036 1 1.445 1 0.365 5 1.600 2 C 1.000 4 1.302 2 0.446 8 1.387 8 D 1.099 7 1.510 5 0.399 3 1.702 1 (25 ms, 42 ms) A 0.554 5 0.505 6 0.457 3 0.630 6 B 0.606 2 0.623 2 0.429 1 0.599 2 C 0.581 8 0.601 7 0.362 7 0.541 0 D 0.527 9 0.503 1 0.395 1 0.503 1 (25 ms, 65 ms) A 0.741 7 0.723 8 0.529 7 0.875 6 B 0.689 9 0.745 2 0.669 0 0.910 1 C 0.713 5 0.758 1 0.632 8 0.943 7 D 0.750 8 0.795 4 0.504 3 0.865 5 -
[1] 楼晓明, 周文海, 简文彬, 等. 基于岩石破碎机理的微差爆破最佳延时控制 [J]. 哈尔滨工业大学学报, 2017, 49(2): 158–163. DOI: 10.11918/j.issn.0367-6234.2017.02.025.LOU Xiaoming, ZHOU Wenhai, JIAN Wenbin, et al. Millisecond blasting optimal time delay control based on rock breaking mechanism [J]. Journal of Harbin Institute of Technology, 2017, 49(2): 158–163. DOI: 10.11918/j.issn.0367-6234.2017.02.025. [2] 田振农, 孟祥栋, 王国欣. 城区隧道电子雷管起爆错相减震机理分析 [J]. 振动与冲击, 2012, 31(21): 108–111. DOI: 10.3969/j.issn.1000-3835.2012.21.022.TIAN Zhennong, MENG Xiangdong, WANG Guoxin. Mechanism analysis of fault-phase vibration reduction for tunnel blasting initiated by electronic detonators in city area [J]. Journal of Vibration and Shock, 2012, 31(21): 108–111. DOI: 10.3969/j.issn.1000-3835.2012.21.022. [3] JOHANSSON D, OUCHTERLONY F. Shock wave interactions in rock blasting: the use of short delays to improve fragmentation in model-scale [J]. Rock Mechanics and Rock Engineering, 2013, 46(1): 1–8. doi: 10.1007/s00603-012-0249-7 [4] 龚敏, 陈哲, 吴昊骏, 等. 掏槽药量与起爆时差的关系对隧道爆破合成振速的影响 [J]. 应用基础与工程科学学报, 2016, 24(6): 1110–1124. DOI: 10.16058/j.issn.1005-0930.2016.06.004.GONG Min, CHEN Zhe, WU Haojun, et al. Influence of correlation between cut basting charge and detonating interval time on superposition vibration velocity caused by millisecond blasting in tunnel [J]. Journal of Basic Science and Engineering, 2016, 24(6): 1110–1124. DOI: 10.16058/j.issn.1005-0930.2016.06.004. [5] ANDERSON D A, WINZER S R, RITTER A P. On computer-aided seismic analysis and discrimina-teon [C] // Proceedings of 3rd International Symposium. Washington DC: 1987: 247−261. [6] 杨年华, 张乐. 爆破振动波叠加数值预测方法 [J]. 爆炸与冲击, 2012, 32(1): 84–90. DOI: 10.11883/1001-1455(2012)02-0084-07.YANG Nianhua, ZHANG Le. Blasting vibration waveform prediction method based on superposition principle [J]. Explosion and Shock Waves, 2012, 32(1): 84–90. DOI: 10.11883/1001-1455(2012)02-0084-07. [7] 郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用 [J]. 岩石力学与工程学报, 2004, 23(19): 3381–3388. doi: 10.3321/j.issn:1000-6915.2004.19.029ZHENG Yingren, ZHAO Shangyi. Application of strength reduction fem in soil and rock slope [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381–3388. doi: 10.3321/j.issn:1000-6915.2004.19.029 [8] 赵铮, 陶钢, 杜长星. 爆轰产物JWL状态方程应用研究 [J]. 高压物理学报, 2009, 23(4): 277–282. doi: 10.3969/j.issn.1000-5773.2009.04.007ZHAO Zheng, TAO Gang, DU Changxing. Application research on JWL equation of state of detonation products [J]. Chinese Journal of High Pressure Physics, 2009, 23(4): 277–282. doi: 10.3969/j.issn.1000-5773.2009.04.007 [9] GRIFFITHS D V, MARQUEZ R M. Three-dimensional slope stability analysis by elasto-plastic finite elements [J]. Geotechnique, 2007, 57(6): 537–546. doi: 10.1680/geot.2007.57.6.537 [10] 赵尚毅, 郑颖人, 张玉芳. 有限元强度折减法中边坡失稳的判据探讨 [J]. 岩土力学, 2005, 26(2): 332–336. DOI: 10.3969/j.issn.1000-7598.2005.02.035.ZHAO Shangyi, ZHENG Yingren, ZHANG Yufang. Study on slope failure criterion in strength reduction finite element method [J]. Rock and Soil Mechanics, 2005, 26(2): 332–336. DOI: 10.3969/j.issn.1000-7598.2005.02.035. [11] SLOAN S W. Geotechnical stability analysis [J]. Geotechnique, 2013, 63(7): 531–572. doi: 10.1680/geot.12.RL.001 [12] 刘柞秋, 周翠英, 董立国, 等. 边坡稳定及加固分析的有限元强度折减法 [J]. 岩土力学, 2005, 26(4): 558–561. DOI: 10.3969/j.issn.1000-7598.2005.04.010.LIU Zuoqiu, ZHOU Cuiying, DONG Liguo, et al. Slope stability and strengthening analysis by strength reduction FEM [J]. Rock and Soil Mechanics, 2005, 26(4): 558–561. DOI: 10.3969/j.issn.1000-7598.2005.04.010. [13] Griffiths D V, Lane P A. Slope stability analysis by finite element [J]. Geotechnique, 1999, 49(3): 387–403. doi: 10.1680/geot.1999.49.3.387 [14] MATSUI T, SAN K C. Finite element slope stability analysis by shear strength reduction technique [J]. Soil and Foundation, 1992, 32(1): 59–70. doi: 10.3208/sandf1972.32.59 [15] 李红, 宫必宁, 陈琰. 有限元强度折减法边坡失稳判据 [J]. 水利与建筑工程学报, 2007, 5(1): 79–82. doi: 10.3969/j.issn.1672-1144.2007.01.025LI Hong, GONG Bining, CHEN Yan. Study on criteria for evaluating stability of slope with fem based on shear strength reduction methods [J]. Journal of Water Resources and Architectural Engineering, 2007, 5(1): 79–82. doi: 10.3969/j.issn.1672-1144.2007.01.025 [16] 楼晓明, 周文海, 简文彬, 等. 微差爆破振动波速度峰值-位移分布特征的延时控制 [J]. 爆炸与冲击, 2016, 36(6): 839–846. DOI: 10.11883/1001-1455(2016)06-0839-08.LOU Xiaoming, ZHOU Wenhai, JIAN Wenbin, et al. Control of delay time characterized by distribution of peak velocity-displacement vibration of millisecond blasting [J]. Explosion and Shock Waves, 2016, 36(6): 839–846. DOI: 10.11883/1001-1455(2016)06-0839-08. -






 下载:
下载: