Analyses of the size effect for projectile penetrations into concrete targets
-
摘要: 由于混凝土靶体抗刚性弹侵彻实验大多基于缩比弹体展开,侵彻深度相似律是否成立显得尤为重要。在侵彻相似模型基础上,综合分析已有侵彻实验数据及经验公式,发现侵彻深度在通常情况下存在尺寸效应,且无量纲侵彻深度随弹体尺寸变大而增大。但如果模型以及原型实验中弹体与混凝土靶体(包括粗骨料)严格等比例设计,侵彻深度相似律是成立的。不变的骨料特征(粗骨料未随弹体尺寸缩放)是引起侵彻实验以及侵彻经验公式中尺寸效应的主要原因。为研究由粗骨料引起的侵彻尺寸效应,开发了混凝土二维细观有限元建模程序,细观数值实验成功地反映出了侵彻尺寸效应,考虑模拟尺寸效应后的侵彻公式能较好地预测不同尺寸侵彻实验。Abstract: Whether the replica scaling law holds or not is of great significance because penetration tests of concrete targets against rigid projectiles are commonly conducted in a reduced scale. In this paper, based on the replica scaling model and the analyses of penetration tests with various sizes and empirical formulae, we found that there exists a size effect in general for penetration depth, and the dimensionless depth increases with as does the size. However, the replica scaling law is satisfied for the penetration depth in rigid projectile penetrations, as long as the scaling is done strictly for both projectiles and concrete targets, including the coarse aggregates. We also found that the coarse aggregates of an invariant size (not replica-scaled) are the major factor accounting for the size effect in penetration depth found in tests and empirical formulae. To find out about the size effect resulting from aggregates, we developed a 2D mesoscopic finite element model for concrete target and conducted numerical simulations that successfully represent the size effect, thereby proving that penetration formula with size effect considered could well predict the penetration tests with different size.
-
Key words:
- penetration depth /
- concrete /
- size effect /
- mesoscopic model
-
表 1 相似模型中原型相对于模型的各物理量
Table 1. Parameters in the prototype model relative to the reduced model
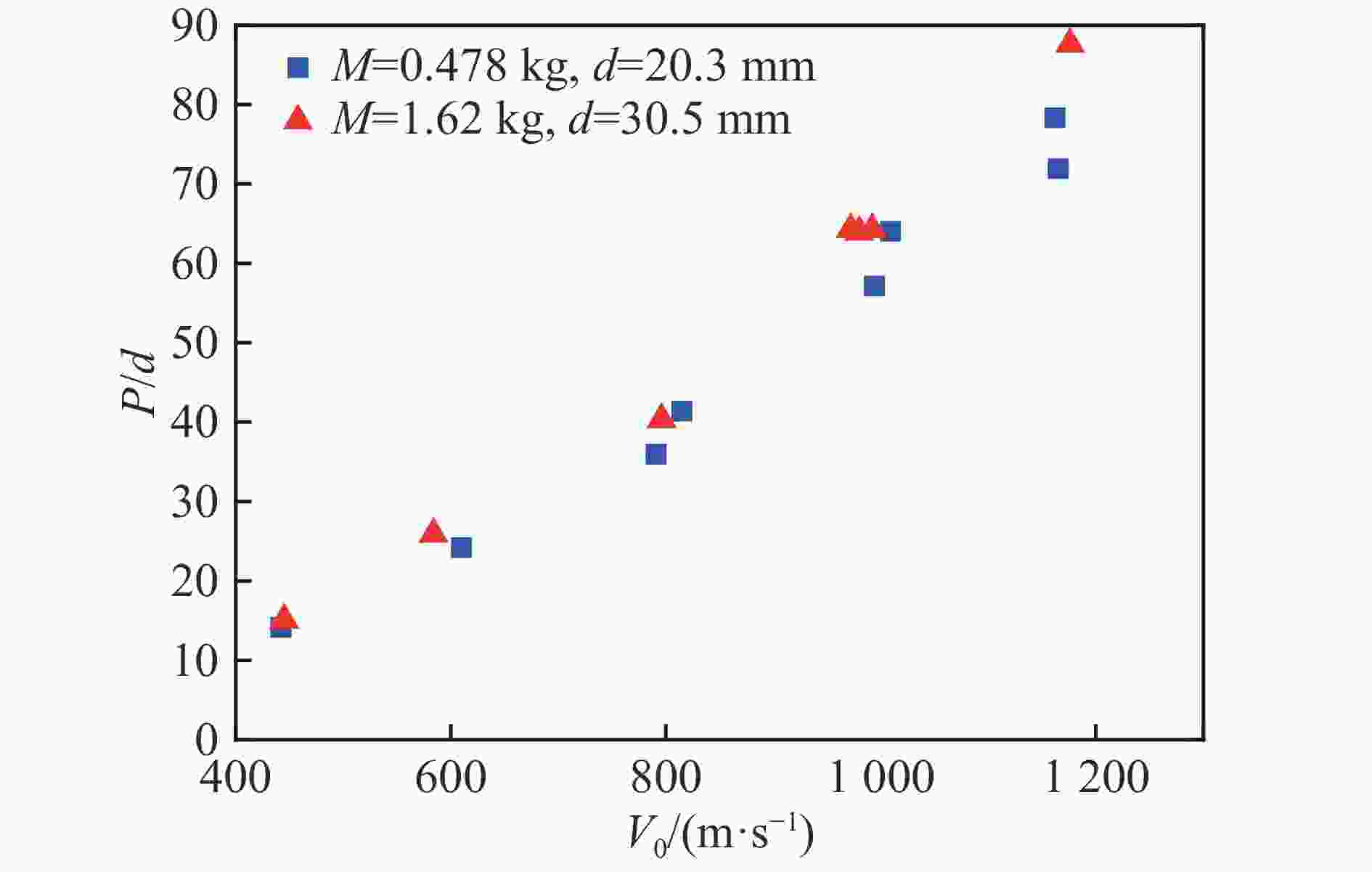
变量 比例 变量 比例 弹径 λ 侵彻深度 λ 弹长 λ 加速度 λ−1 弹体密度 1 侵彻持续时间 λ 弹体质量 λ3 弹体轴向阻力 λ2 侵彻初速度 1 阻应力 1 fc/MPa 13.5 21.6 36.2 51 58.4 62.8 96.7 a1)/mm 4.8 4.8 9.52) 9.5 9.5 9.5 9.52) d/mm 12.9 12.9 26.9 30.5 20.3/30.5 20.3 26.9 d/a 2.69 2.69 2.83 3.21 2.14/3.21 2.14 2.83 M/kg 0.064 0.064 0.906 1.6 0.478/1.62 0.478 0.904 注:1) a 为混凝土靶体中粗骨料的最大粒径,2) 表示粒径没有明确给出。 表 3 砂浆及粗骨料的HJC材料模型参数
Table 3. Parameters of the HJC material model for cement and aggregate
参数 砂浆 骨料 参数 砂浆 骨料 单轴抗压强度 fc/MPa 12 120 弹性极限静水压力Pcrush/MPa 4.0 40 密度 ρ /(kg·m−3) 2 000 2 660 弹性极限体积应变Ucrush 5.4×10−4 1.1×10−3 剪切模量 G/GPa 5.55 26.93 转折静水压力Plock/GPa 1 1 极限面参数A 0.79 0.79 压实体积应变Ulock 0.1 0.1 极限面参数B 1.6 1.6 压力系数K1/GPa 17 17 压力硬化系数 N 0.61 0.61 压力系数K2/GPa 38 38 抗拉强度 T/MPa 1.1 12 压力系数K3/GPa 29.8 29.8 -
[1] FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets [J]. International Journal of Solids and Structures, 1997, 34(31/32): 4127–4146. DOI: 10.1016/S0020-7683(97)00017-6. [2] 吴昊, 方秦, 龚自明. 考虑刚性弹弹头形状的混凝土(岩石)靶体侵彻深度半理论分析 [J]. 爆炸与冲击, 2012, 32(6): 573–580. DOI: 10.11883/1001-1455(2012)06-0573-08.WU Hao, FANG Qin, GONG Ziming. Semi-theoretical analyses for penetration depth of rigid projectiles with different nose geometries into concrete (rock) targets [J]. Explosion and Shock Waves, 2012, 32(6): 573–580. DOI: 10.11883/1001-1455(2012)06-0573-08. [3] FENG J, LI W B, WANG X M, et al. Dynamic spherical cavity expansion analysis of rate-dependent concrete material with scale effect [J]. International Journal of Impact Engineering, 2015, 84: 24–37. DOI: 10.1016/j.ijimpeng.2015.05.005. [4] KONG X Z, WU H, FANG Q, et al. Rigid and eroding projectile penetration into concrete targets based on an extended dynamic cavity expansion model [J]. International Journal of Impact Engineering, 2017, 100: 13–22. DOI: 10.1016/j.ijimpeng.2016.10.005. [5] KONG X Z, FANG Q, WU H, et al. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model [J]. International Journal of Impact Engineering, 2016, 95: 61–71. DOI: 10.1016/j.ijimpeng.2016.04.014. [6] LI Q M, REID S R, WEN H M, et al. Local impact effects of hard missiles on concrete targets [J]. International Journal of Impact Engineering, 2005, 32(1): 224–284. [7] FORRESTAL M J, ALTMAN B S, CARGILE J D. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. DOI: 10.1016/0734-743X(94)80024-4. [8] FREW D J, HANCHAK S J, GREEN M L, et al. Penetration of concrete targets with ogive-nose steel rods [J]. International Journal of Impact Engineering, 1998, 21(6): 489–497. DOI: 10.1016/S0734-743X(98)00008-6. [9] 周宁, 任辉启, 沈兆武, 等. 弹丸侵彻混凝土和钢筋混凝土的试验 [J]. 中国科学技术大学学报, 2016, 36(10): 1021–1027.ZHOU Ning, REN Huiqi, SHEN Zhaowu, et al. Experimental on the projectile penetration concrete targets and reinforced concrete targets [J]. Journal of University of Science and Technology of China, 2016, 36(10): 1021–1027. [10] LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile [J]. International Journal of Impact Engineering, 2003, 28(1): 93–116. DOI: 10.1016/S0734-743X(02)00037-4. [11] PENG Y, WU H, FANG Q, et al. A note on the deep penetration and perforation of hard projectiles into thick targets [J]. International Journal of Impact Engineering, 2015, 85: 37–44. DOI: 10.1016/j.ijimpeng.2015.06.013. [12] 徐建波. 长杆射弹对混凝土的侵彻特性研究[D]. 长沙: 国防科学技术大学, 2001: 79−84. [13] 许三罗, 相恒波. 射弹侵彻混凝土中相似理论的应用及误差分析 [J]. 弹箭与制导学报, 2007, 27(3): 123–126. DOI: 10.3969/j.issn.1673-9728.2007.03.037.XU Sanluo, XIANG Hengbo. Similarity theory applied in projectile penetrating into concrete target and deflection analysis [J]. Journal of Projectile, Rocket, Missiles and Guidance, 2007, 27(3): 123–126. DOI: 10.3969/j.issn.1673-9728.2007.03.037. [14] 卢江仁, 孟会林, 孙新利. 动能弹垂直侵彻混凝土相似律的数值模拟研究 [J]. 弹箭与制导学报, 2007, 27(4): 145–147. DOI: 10.3969/j.issn.1673-9728.2007.04.043.LU Jiangren, MENG Huilin, SUN Xinli. Numerical simulation of the analogue rules of the kinetic energy projectile vertically penetrating concrete target [J]. Journal of Projectile, Rocket, Missiles and Guidance, 2007, 27(4): 145–147. DOI: 10.3969/j.issn.1673-9728.2007.04.043. [15] 高光发, 李永池, 罗春涛, 等. 混凝土靶高速侵彻的率相关相似律研究 [J]. 弹箭与制导学报, 2011, 31(3): 98–100. DOI: 10.3969/j.issn.1673-9728.2011.03.028.GAO Guangfa, LI Yongchi, LUO Chuntao, et al. The study on rate-dependent similarity law of high velocity penetration into concrete target [J]. Journal of Projectile, Rocket, Missiles and Guidance, 2011, 31(3): 98–100. DOI: 10.3969/j.issn.1673-9728.2011.03.028. [16] FORRESTAL M J, FREW D J, HICKERSON J P, et al. Penetration of concrete targets with deceleration-time measurements [J]. International Journal of Impact Engineering, 2003, 28(5): 479–497. DOI: 10.1016/S0734-743X(02)00108-2. [17] GOMEZ J T, SHUKLA A. Multiple impact penetration of semi-infinite concrete [J]. International Journal of Impact Engineering, 2001, 25(10): 965–979. DOI: 10.1016/S0734-743X(01)00029-X. [18] HANCHAK S J, FORRESTAL M J, YOUNG E R, et al. Perforation of concrete slab with 48MPa (7ksi) and 140MPa (20ksi) unconfined compressive strength [J]. International Journal of Impact Engineering, 1992, 12(1): 1–7. DOI: 10.1016/0734-743X(92)90282-X. [19] FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles [J]. International Journal of Impact Engineering, 1996, 18(5): 465–476. DOI: 10.1016/0734-743X(95)00048-F. [20] ACE Fundamentals of protective structures[R]. Army Corps of Engineers, Office of the Chief of Engineers, 1946. [21] Effects of impact and explosion[R]. Washington D C: National Defense Research Committee, 1946. [22] TELAND J A, SJØL H. An examination and reinterpretion of experimental data behind various empirical equations for penetration into concrete[C] //Proceedings of the 9th International Symposium Interaction of the Effects of Munitions with Structures, 1999. [23] BLUDAU C, KEUSER M, KUSTERMANN A. Perforation resistance of high-strength concrete panels [J]. ACI Structural Journal, 2006, 103(2): 188–195. [24] ZHANG M H, SHIM V P W, LU G, et al. Resistance of high-strength concrete to projectile impact [J]. International Journal of Impact Engineering, 2005, 31(7): 825–841. DOI: 10.1016/j.ijimpeng.2004.04.009. [25] CANFIELD J A, CLATOR I G. Development of a scaling law and techniques to investigate penetration in concrete: 2057 [R] Dahlgren: Naval Weapons Laboratory, 1966. [26] MANUAL L S D K U, Volume I. Version 971 [M]. Livermore Software Technology Corporation, 2007: 500−600. [27] HOLMQUIST T J, JOHNSON G R, Cook W H. A computational constitutive model for concrete subjective to large strain, high strain rates, and high pressure[C] // Proceedings of the 14th International Symposium on Ballistic. Canada, Quebec City, 1993: 591−600. [28] 彭永. 单(多)层混凝土靶板抗弹体侵彻/贯穿研究[D]. 南京: 解放军理工大学, 2014: 84−87. -






 下载:
下载: