A multi-component Duan-Zhang-Kim mesoscopic reaction rate model for shock initiation of multi-component PBX explosives
-
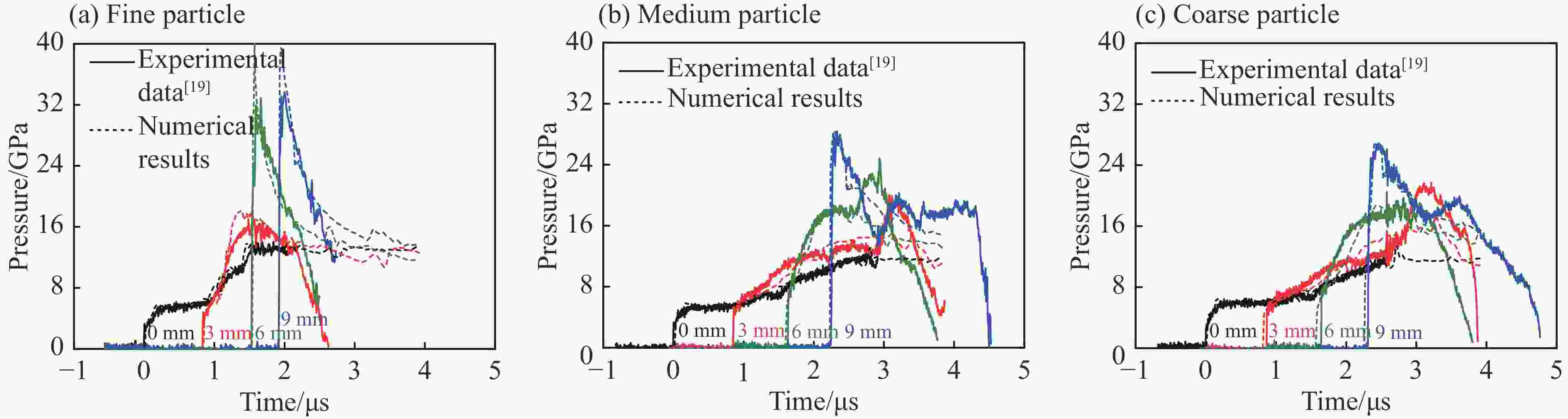
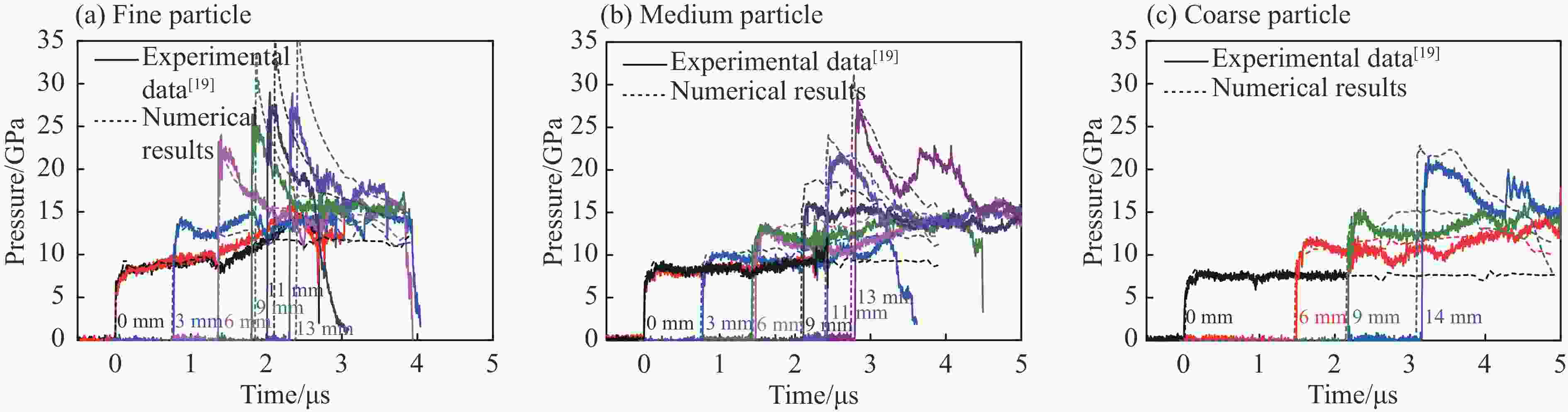
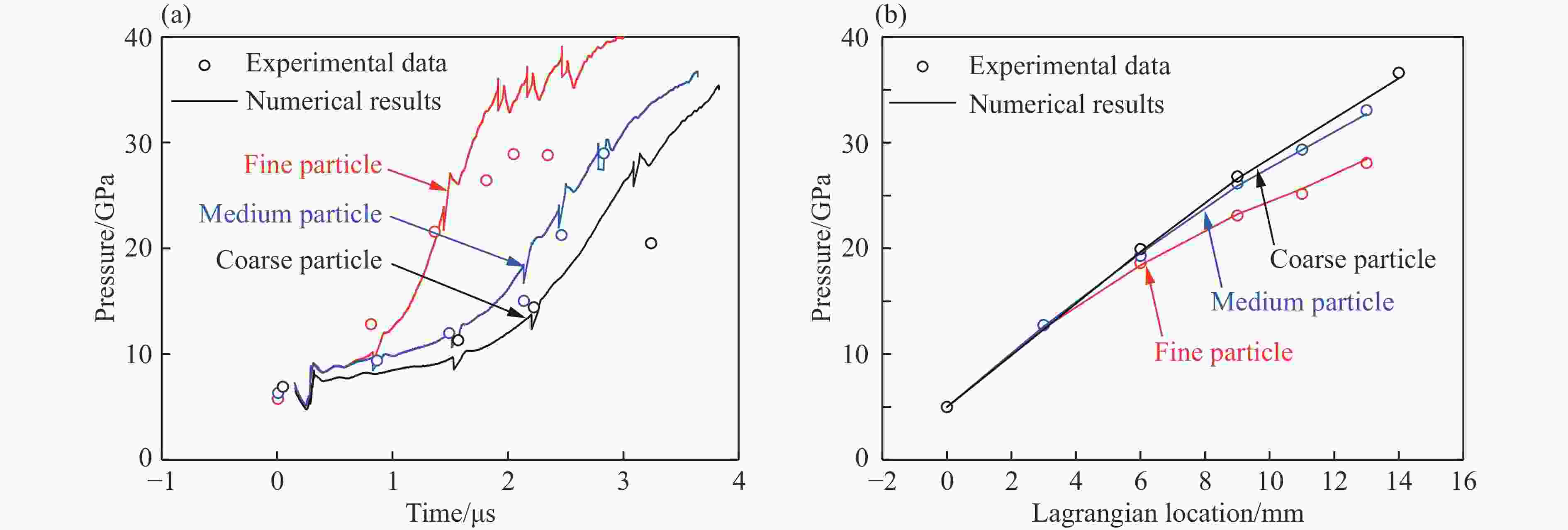
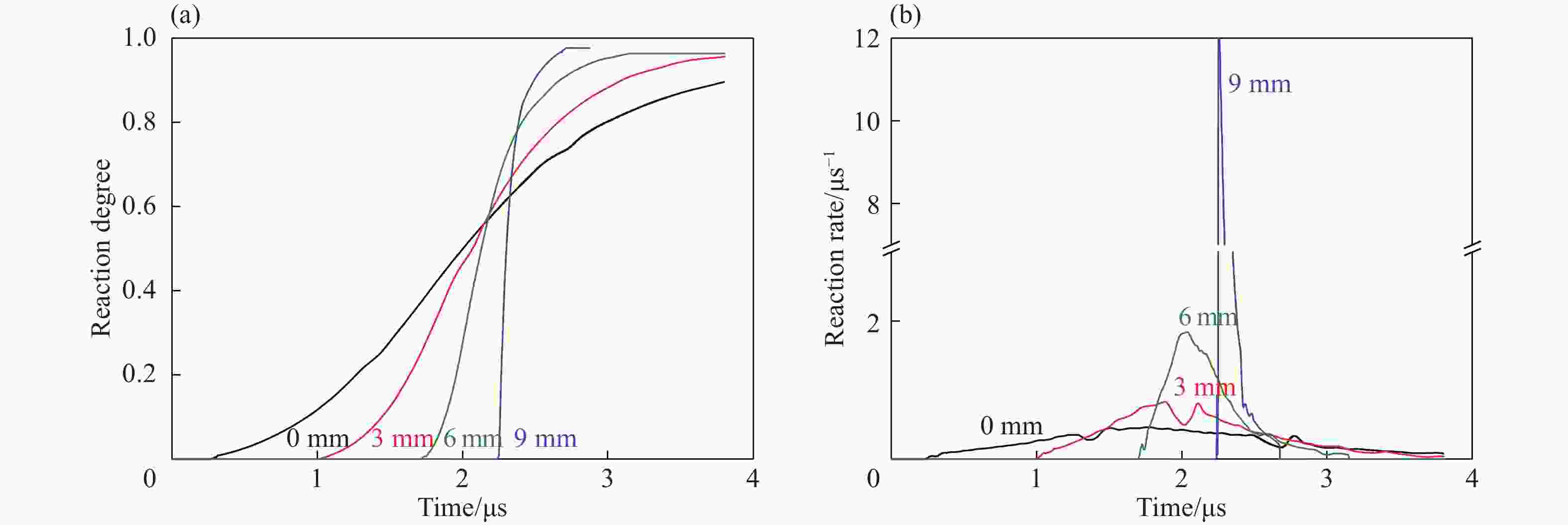
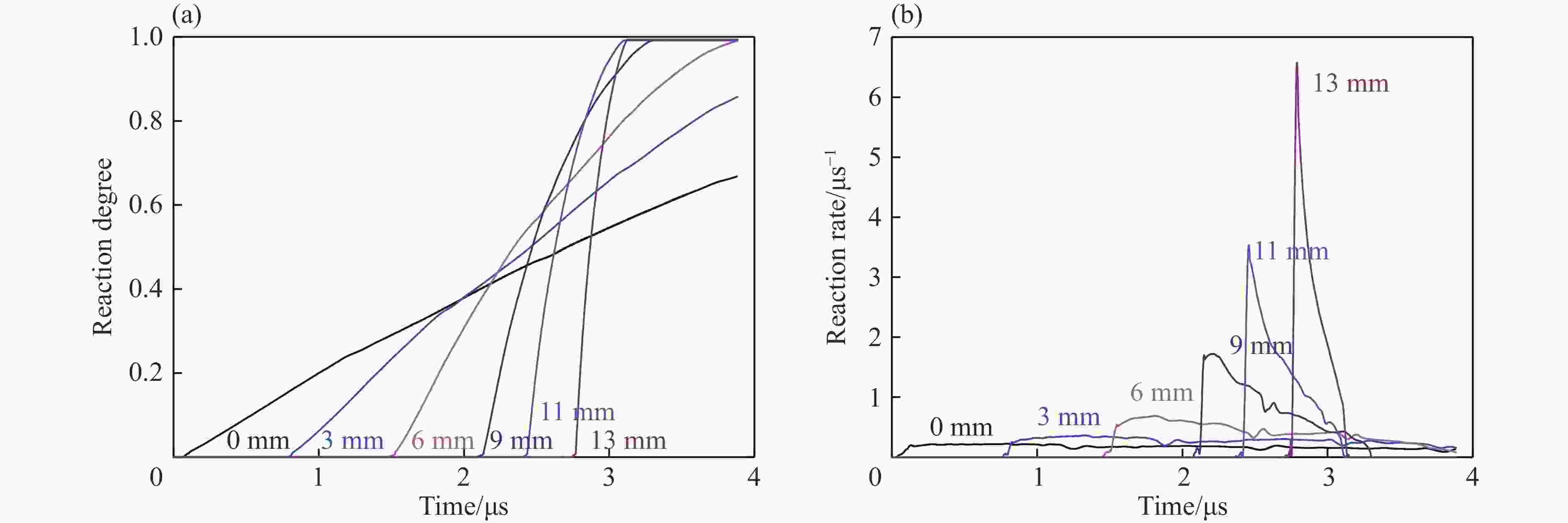
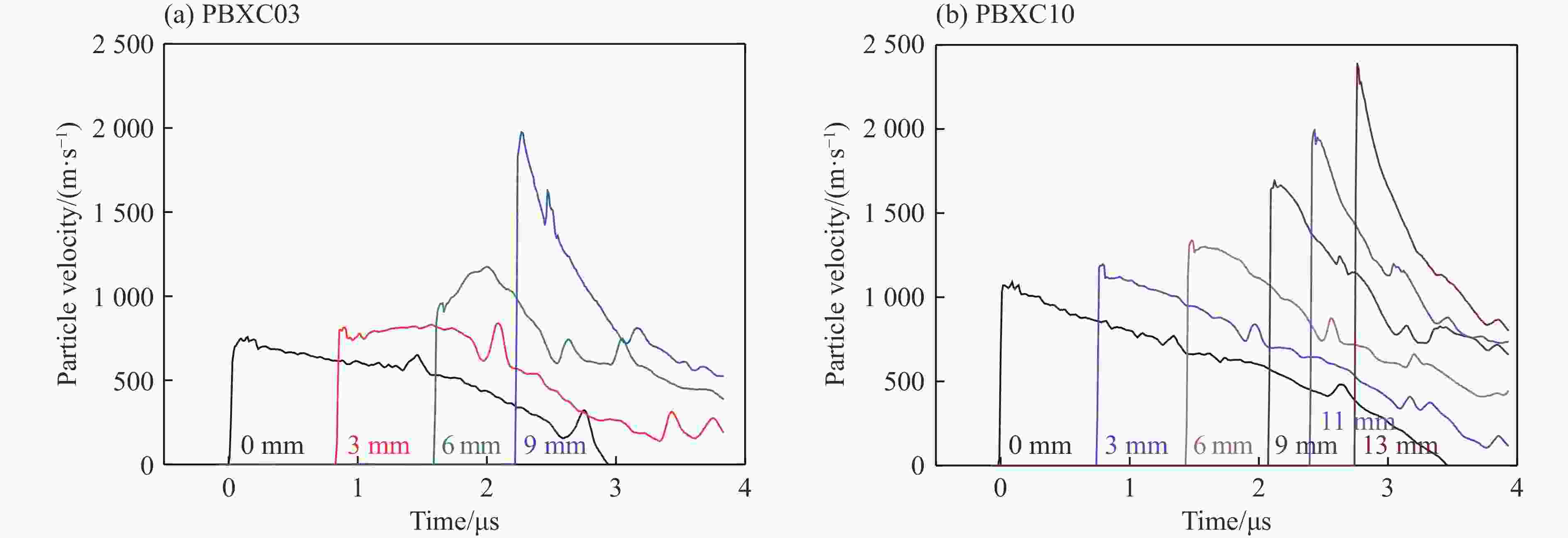
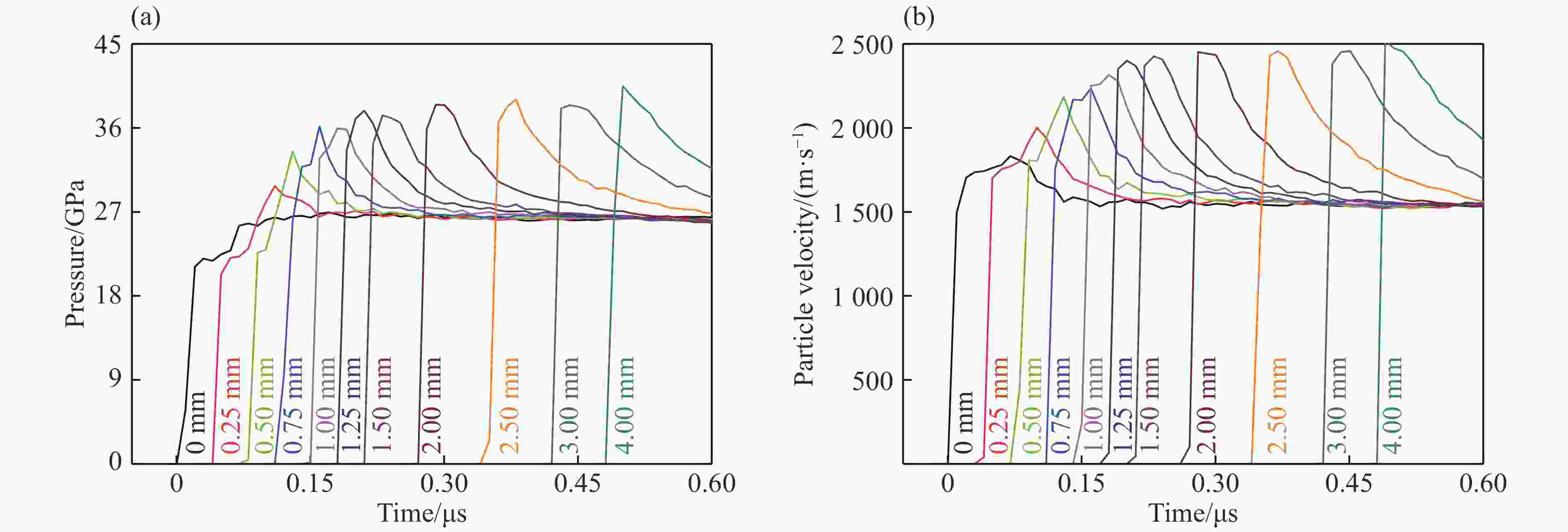
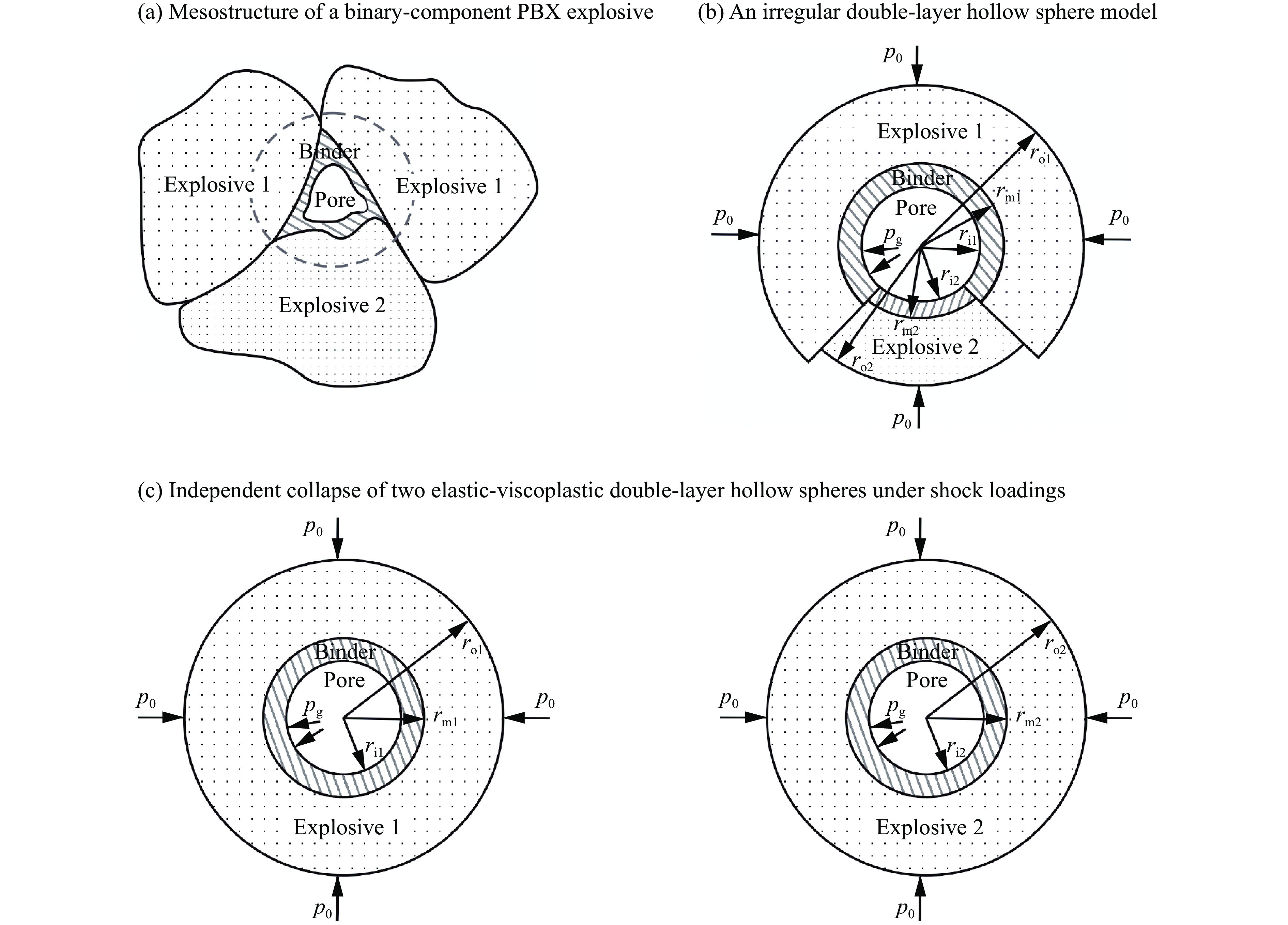
摘要: 提出了多元混合PBX炸药孔隙塌缩热点模型新的处理方法，构建了新的细观反应速率模型，系列数值模拟结果与实验结果均一致，表明该细观反应速率模型可较好地描述和预测炸药组分配比及颗粒度对多元混合PBX炸药冲击起爆过程的影响。PBX炸药冲击起爆过程主要受热点点火过程和燃烧反应过程共同作用：HMX占主导成分的PBXC03炸药，起爆压力低，冲击起爆过程受热点点火影响较明显，热点点火后的燃烧反应速度较快，表现为加速反应特性；TATB占主导成分的钝感PBXC10炸药，起爆压力高，冲击起爆过程主要受点火后的燃烧反应过程控制，且点火后燃烧反应速度较慢，表现为稳定反应特性。Abstract: This paper offers a new method for calculating the reaction rate of the pore collapse hot-spot ignition in multi-component PBX explosives, and proposes a new mesoscopic reaction rate model capable of describing and predicting the shock initiation and detonation behavior of multi-component PBX explosives with any explosive components proportion as well as any explosive particle size. The pressure-time histories in the explosive samples calculated using this mesoscopic reaction rate model are in good agreement with the experimental data. The shock initiation and detonation process of PBX explosives is mainly controlled by both the hot-spot ignition processes and the combustion reaction processes. The PBXC03 explosive with the dominant component of HMX is mainly controlled by the hot-spot ignition and shows the accelerated reaction characteristics. With the dominant component of insensitive TATB, the critical initiation pressure of PBXC10 is high and the shock initiation behavior is controlled by the combustion reaction process, which shows a stable reaction characteristics.
-
图 1 弹黏塑性不规则双球壳塌缩热点模型分解为2个独立的弹黏塑性双球壳塌缩热点模型
Figure 1. Illustration of dividing an irregular double-layer hollow sphere model into two spherically-symmetric double-layer hollow sphere models for a two-component PBX explosive
图 2 PBX9501和LX-17炸药内不同拉格朗日位置的压力历史曲线
Figure 2. Pressure-time histories at different Lagrange positions in HMX-based PBX9501 and TATB-based LX-17
图 3 不同颗粒度PBXC03炸药内不同拉格朗日位置的压力成长历史
Figure 3. Pressure-time histories at different Lagrange locations in PBXC03 with different particle sizes
图 4 不同颗粒度PBXC10炸药内不同拉格朗日位置的压力成长历史
Figure 4. Pressure-time histories at different Lagrange locations in PBXC10 with different particle sizes
图 5 不同颗粒度的PBXC03炸药前导冲击波阵面压力成长历史和前导冲击波迹线
Figure 5. Pressure growth histories on precursory shock wave front and precursory shock wave trajectories in PBXC03 with different particle sizes
图 6 不同颗粒度的PBXC10炸药前导冲击波阵面压力成长历史和前导冲击波迹线
Figure 6. Pressure growth histories on precursory shock wave front and precursory shock wave trajectories in PBXC10 with different particle sizes
图 7 PBXC03炸药在不同拉格朗日位置的反应度-时间曲线和反应速率-时间曲线
Figure 7. Typical reaction degree-time histories and reaction rate-time histories at different Lagrange locations in PBXC03
图 8 PBXC10炸药在不同拉格朗日位置的反应度-时间曲线和反应速率-时间曲线
Figure 8. Typical reaction degree-time histories and reaction rate-time histories at different Lagrange locations in PBXC10
图 9 PBXC03和PBXC10炸药不同拉格朗日位置的产物粒子速度-时间历史
Figure 9. Typical particle velocity-time histories at different Lagrange locations in PBXC03 and PBXC10
图 10 PBXC03 and PBXC10炸药中不同拉格朗日位置的前导冲击波阵面迹线、峰值粒子速度迹线、峰值化学反应速率迹线和峰值压力迹线
Figure 10. Trajectories of precursory shock wave, peak particle velocity, peak reaction rate and peak pressure at different Lagrange locations in PBXC03 and PBXC10
图 11 铝飞片以2 800 m/s的速度撞击PBXC03炸药的冲击起爆过程中不同拉格朗日位置的压力历史和粒子速度历史的计算结果
Figure 11. Numerical results for pressure-time histories and particle velocity-time histories at different Lagrange locations in PBXC03 impacted by an Al flyer with the velocity of 2 800 m/s
表 1 常温下PBXC03和PBXC10炸药中HMX和TATB的热点点火项参数[19]
Table 1. Thermodynamic parameters of hot-spot ignition terms for HMX and TATB[19]
炸药组分l=1,2 Zl/μs−1 Tl*/K T0l/K γel/μs−1 cpl/(cm2·μs−2·K−1) kel/MPa Ql/(g·μs−2·cm−1) HMX 5.0×1013 26 500 298 0.026 1.4×10−5 8 5.439×10−2 TATB 3.18×1019 30 140.8 298 0.026 2.005×10−5 8 2.510×10−2 
下载: 导出CSV
表 2 PBX9501和LX-17炸药的反应速率模型第二、三项系数
Table 2. Parameters of the second and the third terms in Eq.(5) for PBX9501 and LX-17
炸药组分(l=1,2) al bl nl Gl ml sl PBX9501(HMX基) 0.027 2.05 1.00 800.0 3.355 1.00 LX-17(TATB基) 0.01 1.70 2.03 220.0 3.077 0.2
下载: 导出CSV
表 3 PBXC03和PBXC10炸药中各取代基体的体积分数
Table 3. Volume fractions of each substituted explosive component in PBXC10 and PBXC03
体积分数 PBX9501(HMX基) PBXC03 PBXC10 LX-17(TATB基) χ1 1 0.923 193 0.247 764 0 χ2 0 0.076 807 0.752 236 1
下载: 导出CSV
表 4 PBXC03和PBXC10炸药组分配比及物理参数[19]
Table 4. Components proportions and physical parameters of PBXC03 and PBXC10[19]
炸药名称 组分及配比 装药密度
ρ/(g·cm−3)理论密度
ρt /(g·cm−3)平均颗粒度/μm HMX/TATB/黏结剂 重量/% 体积/% HMX TATB PBXC03 87/7/6 85.58/6.76/7.66 1.849 1.873 20～30 (细颗粒) 70～90 (中等颗粒) 100～130 (粗颗粒) 15 PBXC10 25/70/5 25.4/69.8/4.8 1.900 1.934
下载: 导出CSV
表 5 PBXC03和PBXC10炸药爆轰产物和未反应炸药状态方程参数[19]
Table 5. JWL EOS parameters for detonation products and unreacted PBXC03 and PBXC10[19]
参数 PBXC03 PBXC10 爆轰产物 未反应炸药 爆轰产物 未反应炸药 A/GPa 1 025.45 27 213 759.0 612.8 12 734.089 B/GPa 22.57 −73.854 4 18.58 −8.982 0 R1 4.91 19.87 4.32 10.4 R2 1.37 1.987 1.79 1.04 ω 0.29 1.99 0.21 2.50 cV/(GPa·K−1) 1.0×10−3 1.693 2×10−2 1.0×10−3 3.731 22×10−2 E0/GPa 10.0 — 10.0 —
下载: 导出CSV
-
[1] BOLTON O, SIMKE L R, PAGORIA P F, et al. High power explosive with good sensitivity: a 2:1 cocrystal of CL-20: HMX [J]. Crystal Growth and Design, 2012, 12(9): 4311–4314. DOI: 10.1021/cg3010882. [2] TARVER C M, TRAN T D. Thermal decomposition models for HMX-based plastic bonded explosives [J]. Combustion and Flame, 2004, 137(1/2): 50–62. DOI: 10.1016/j.combustflame.2004.01.002. [3] URTIEW P A, FORBES J W, GARCIA F, et al. Shock Initiation of UF-TATB at 250 ℃ [C] // FURNISH M D, HORIE Y, THADHANI N N. Shock Compression of Condensed Matter-2001. United States: American Institute of Physics, 2002: 1039−1042. DOI: 10.1063/1.1483716. [4] AN Chongwei, LI Hequn, YE Baoyun, et al. Preparation and characterization of ultrafine HMX/TATB explosive co-crystals [J]. Central European Journal of Energetic Materials, 2017, 14(4): 876–887. DOI: 10.22211/cejem/77125. [5] WANG Z, GUO X, WU F, et al. Preparation of HMX/TATB composite particles using a mechanochemical approach [J]. Propellants, Explosives, Pyrotechnics, 2016, 41(2): 327–333. DOI: 10.1002/prep.201500136. [6] GREBENKIN K F. Comparative analysis of physical mechanisms of detonation initiation in HMX and in a low-sensitive explosive (TATB) [J]. Combustion, Explosion, and Shock Waves, 2009, 45(1): 78–87. DOI: 10.1007/s10573-009-0011-y. [7] AUSTIN R, BARTON N, HOWARD W, et al. Modeling pore collapse and chemical reactions in shock-loaded HMX crystals [J]. Journal of Physics: Conference Series, 2014, 500(5): 052002–052007. DOI: 10.1088/1742-6596/500/5/052002. [8] KAPAHI A. Dynamics of void collapse in shocked energetic materials: physics of void-void interactions [J]. Shock Waves, 2013, 23(6): 537–558. DOI: 10.1007/s00193-013-0439-6. [9] OZLEM M, SCHWENDEMAN D W, KAPILA A K, et al. A numerical study of shock-induced cavity collapse [J]. Shock Waves, 2012, 22(2): 89–117. DOI: 10.1007/s00193-011-0352-9. [10] TRAN L, UDAYKUMAR H S. Simulation of void collapse in an energetic material: Part 1: inert case [J]. Journal of Propulsion and Power, 2006, 22(5): 947–958. DOI: 10.2514/1.13146. [11] ZHOU Tingting, LOU Jianfeng, ZHANG Yangeng, et al. Hot spot formation and chemical reaction initiation in shocked HMX crystals with nanovoids: a large-scale reactive molecular dynamics study [J]. Physical Chemistry Chemical Physics, 2016, 18(26): 17627–17645. DOI: 10.1039/C6CP02015A. [12] MASSONI J, SAUREL R, BAUDIN G, et al. A mechanistic model for shock initiation of solid explosives [J]. Physics of Fluids, 1999, 11(3): 710–736. DOI: 10.1063/1.869941. [13] SOUERS P C, GARZA R, VITELLO P. Ignition & growth and JWL++ detonation models in coarse zones [J]. Propellants, Explosives, Pyrotechnics, 2002, 27(2): 62–71. DOI: 10.1002/1521-4087(200204)27:23.0.CO;2-5. [14] STARKENBERG J. Modeling detonation propagation and failure using explosive initiation models in a conventional hydrocode [C] // SHOR J M, MAIENSCHEIN J L. The 12th Symposium (International) on Detonation. USA: Office of Naval Research, 2002: 1001−1007. [15] SHAW M S, MENIKOFF R. A reactive burn model for shock initiation in a PBX: scaling and separability based on the hot spot concept [C] // PEIRIS C B S, ASAY B. The 14th Symposium (International) on Detonation. USA: Office of Naval Research, 2010. [16] DUAN Zhuoping, WEN Lijing, LIU Yan, et al. A pore collapse model for hot-spot ignition in shocked multi-component explosives [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2010, 11(S): 19–24. DOI: 10.1515/IJNSNS.2010.11.S1.19. [17] KIM K. Development of a model of reaction rates in shocked multicomponent explosives [C] // LEE E L, SHORT J M. The 9th Symposium (International) on Detonation. USA: Office of the Chief of Naval Researche, 1989: 593−603. [18] WEN Lijing, DUAN Zhuoping, ZHANG Liansheng, et al. Effects of HMX particle size on the shock initiation of PBXC03 explosive [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2012, 13(2): 189–194. DOI: 10.1515/ijnsns.2011.129. [19] 温丽晶. PBX炸药冲击起爆细观反应速率模型研究[D]. 北京: 北京理工大学, 2011.WEN Lijing. Research on mesoscopic reaction rate model of shock initiation of PBX [D]. Beijing: Beijing Institute of Technology, 2011. [20] LIU Y R, DUAN Z P, ZHANG Z Y, et al. A mesoscopic reaction rate model for shock initiation of multi-component PBX explosives [J]. Journal of Hazardous Materials, 2016, 317: 44–51. DOI: 10.1016/j.jhazmat.2016.05.052. [21] URTIEW P A, TARVER C M. Shock initiation of energetic materials at different initial temperatures: review [J]. Combustion, Explosion, and Shock Waves, 2005, 41(6): 766–776. DOI: 10.1007/s10573-005-0085-0. [22] URTIEW P A, VANDERSALL K S, TARVER C M, et al. Initiation of heated PBX-9501 explosive when exposed to dynamic loading: UCRL-CONF-214667 [R]. United States: Lawrence Livermore National Laboratory, 2005. -
计量
- 文章访问数: 5189
- HTML全文浏览量: 1794
- PDF下载量: 64
- 被引次数: 0