Analytical model for attitude deflection of rigid projectile during oblique perforation of concrete targets
-
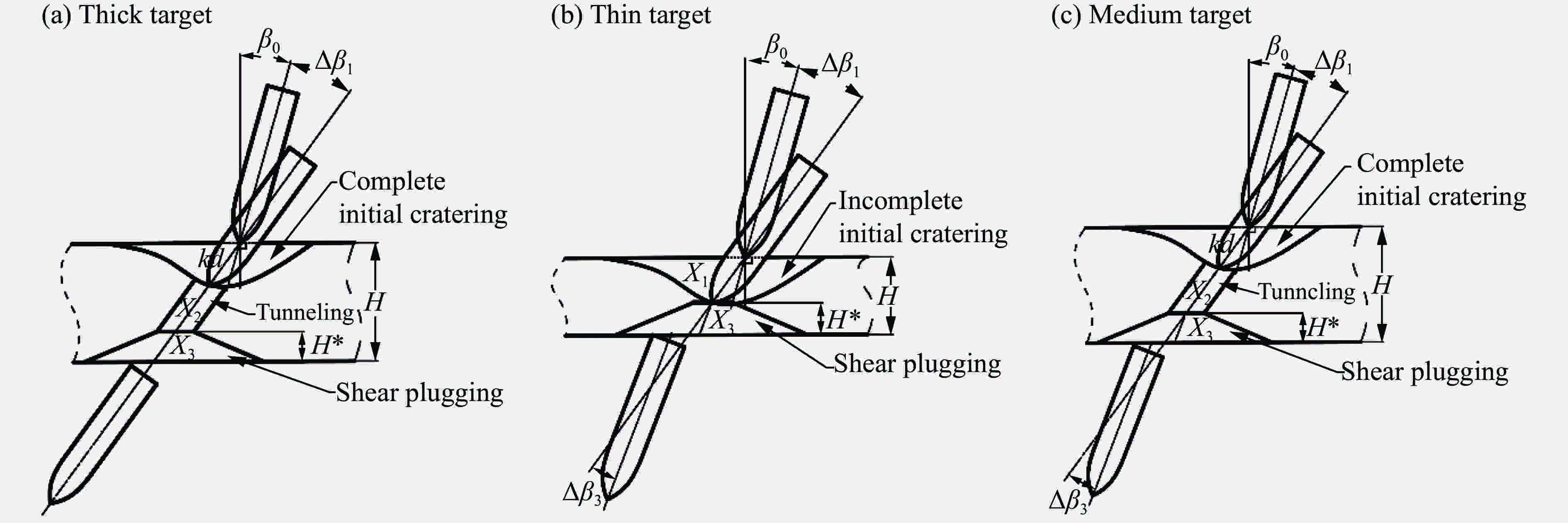
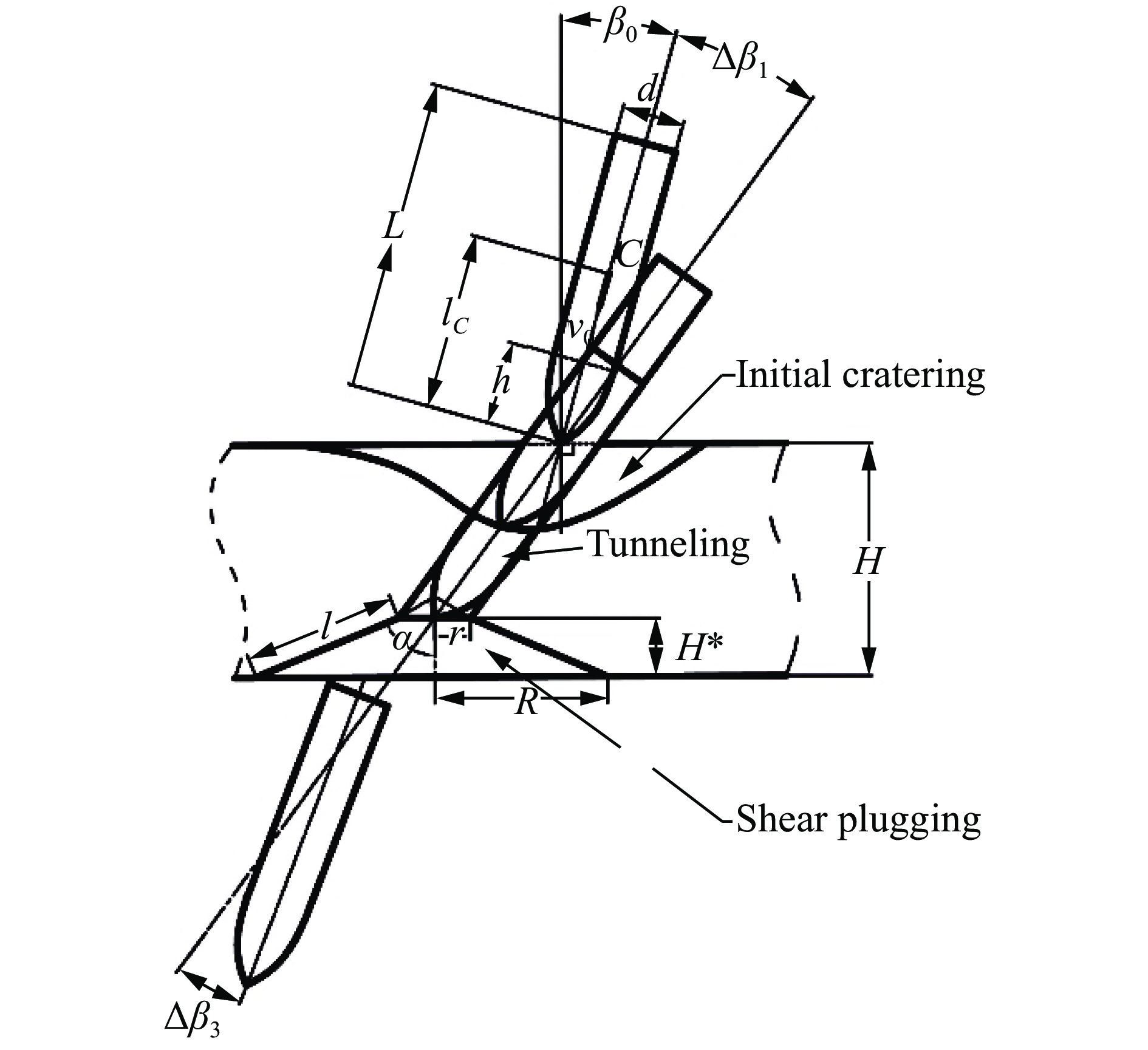
摘要: 为描述刚性弹体斜侵彻贯穿混凝土靶的弹体姿态变化，针对已有贯穿模型存在的问题，在斜侵彻贯穿过程中考虑了弹体转动惯量对姿态偏转的影响，根据弹体贯穿靶板后的成孔特性重新假设了背靶面崩落块形状，并在弹体贯穿出靶的剪切冲塞阶段引入了弹体姿态二次偏转机制，从而建立了刚性弹体斜侵彻贯穿混凝土靶的姿态偏转理论模型，同时给出了混凝土薄靶、中厚靶和厚靶的分类方法。多种侵彻状态的理论模型计算结果均与实验测量结果吻合较好，表明本文理论模型可有效预估弹体斜侵彻贯穿混凝土靶的弹体出靶姿态。Abstract: In the present study we developed an analytical model to describe the attitude deflection of the rigid projectile obliquely penetrating into concrete targets. To improve on the previous models, we took the effect of the inertia moment of the projectile into account and assumed anew the shape of the plug formed on the rear surface of the concrete target with regard to the experimental perforation characteristics, and introduced a second attitude deflection mechanism into the shear plugging stage. Moreover, we proposed to classify concrete targets into three types, i.e. thin, medium and thick. The calculated results under different perforation situations accorded well with the experimental data, indicating the validity of our analytical model in predicting the projectile attitude during the oblique perforation of concrete targets.
-
Key words:
- rigid projectile /
- oblique perforation /
- penetration /
- concrete target /
- attitude deflection
-
图 1 弹体斜侵彻贯穿混凝土靶过程中各阶段弹体姿态偏转过程示意图
Figure 1. Illustrated attitude deflection of the projectile in each stage during the oblique perforation of concrete targets
图 2 弹体斜侵彻贯穿不同厚度混凝土靶时弹体姿态的偏转过程
Figure 2. Attitude deflection of the projectile in oblique perforation of concrete targets with different thickness.
表 1 垂直侵彻普通强度(48 MPa)钢筋混凝土靶弹体出靶剩余速度的实验结果与计算结果[15]
Table 1. Experimental data and numerical results of the residual velocities in normal perforation of the normal strength (48 MPa) reinforced concrete targets[15]
弹体质量/
kg靶厚/
m初始速度/
(m·s−1)弹体出靶剩余速度/(m·s−1) 相对误差/
%实验结果[15] 计算结果 0.5 0.127 301 0 0 0 360 67 79 17.9 381 136 150 10.3 434 214 250 16.8 606 449 482 7.3 746 605 641 6.0 749 615 645 4.9 1 058 947 973 2.7 
下载: 导出CSV
表 2 斜侵彻贯穿多层间隔混凝土薄靶实验中弹体出靶剩余速度的实验结果和计算结果
Table 2. Experimental data and numerical results of the residual velocities in oblique perforation of the multi-layered thin concrete targets
实验序号 靶厚/
m初始速度/
(m·s−1)弹体出靶剩余速度/(m·s−1) 相对误差/
%实验结果[10] 计算结果 1-1 0.30 833 820 827 0.9 1-2 0.18 820 800 818 2.3 1-3 0.18 800 771 798 3.5 2-1 0.30 688 684 681 0.4 2-2 0.18 684 669 679 1.5
下载: 导出CSV
表 3 斜侵彻贯穿多层间隔混凝土薄靶实验中弹体出靶姿态偏转角的实验结果和计算结果
Table 3. Experimental data and numerical results of the attitude deflection angles in oblique perforation of the multi-layered thin concrete targets
实验序号 靶厚/
m初始姿态角/
(°)弹体出靶姿态偏转角/(°) 绝对误差/
(°)实验结果[10] 计算结果 1-1 0.30 15.0 −0.9 −1.00 0.10 1-2 0.18 14.1 −0.1 −0.30 0.20 1-3 0.18 14.0 −0.2 −0.30 0.10 2-1 0.30 14.7 −1.6 −1.40 0.20 2-2 0.18 13.1 −0.4 −0.42 0.02
下载: 导出CSV
-
[1] 王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2005: 39−64. [2] 薛建峰, 沈培辉, 王晓鸣. 弹体斜侵彻混凝土靶的实验研究及其数值模拟 [J]. 爆炸与冲击, 2017, 37(3): 536–543. DOI: 10.11883/1001-1455(2017)03-0536-08.XUE Jianfeng, SHEN Peihui, WANG Xiaoming. Experimental study and numerical simulation of projectile obliquely penetrating into concrete target [J]. Explosion and Shock Waves, 2017, 37(3): 536–543. DOI: 10.11883/1001-1455(2017)03-0536-08. [3] 汪斌, 曹仁义, 谭多望. 大质量高速动能弹侵彻钢筋混凝土的实验研究 [J]. 爆炸与冲击, 2013, 33(1): 98–102. DOI: 10.11883/1001-1455(2013)01-0098-05.WANG Bin, CAO Renyi, TAN Duowang. Experimental study on penetration of reinforced concrete by a high-speed penetrator with large mass [J]. Explosion and Shock Waves, 2013, 33(1): 98–102. DOI: 10.11883/1001-1455(2013)01-0098-05. [4] 何翔, 徐翔云, 孙桂娟, 等. 弹体高速侵彻混凝土的效应实验 [J]. 爆炸与冲击, 2010, 30(1): 1–6. DOI: 10.11883/1001-1455(2010)01-0001-06.HE Xiang, XU Xiangyun, SUN Guijuan, et al. Experimental investigation on projectiles’ high-velocity penetration into concrete targets [J]. Explosion and Shock Waves, 2010, 30(1): 1–6. DOI: 10.11883/1001-1455(2010)01-0001-06. [5] 吕中杰, 徐钰巍, 黄风雷. 弹体斜侵彻混凝土过程中的方向偏转 [J]. 兵工学报, 2009, 30(2): 301–304.LYU Zhongjie, XU Yuwei, HUANG Fenglei. Transverse deflection of projectile obliquely penetrating into concrete [J]. Acta Armamentarii, 2009, 30(2): 301–304. [6] CHEN X W, FAN S C, LI Q M. Oblique and normal perforation of concrete targets by a rigid projectile [J]. International Journal of Impact Engineering, 2004, 30: 617–637. doi: 10.1016/j.ijimpeng.2003.08.003 [7] CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. doi: 10.1016/S0734-743X(02)00005-2 [8] LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile [J]. International Journal of Impact Engineering, 2003, 28: 93–116. doi: 10.1016/S0734-743X(02)00037-4 [9] 马兆芳, 段卓平, 欧卓成, 等. 弹体斜侵彻多层间隔混凝土靶实验和数值模拟 [J]. 北京理工大学学报, 2016, 36(10): 1001–1005.MA Zhaofang, DUAN Zhuoping, OU Zhuocheng, et al. Experimental and simulative research on projectile oblique penetration into concrete targets with multi-layered space structure [J]. Transactions of Beijing Institute of Technology, 2016, 36(10): 1001–1005. [10] 马兆芳. 动能弹斜侵彻有限厚混凝土靶体的弹道规律研究 [D]. 北京: 北京理工大学, 2016: 12−26. [11] IPSON T W, RECHT R F. Ballistic penetration resistance and its measurement [J]. Experimental Mechanics, 1975, 15: 249–257. doi: 10.1007/BF02318057 [12] 薛建锋, 沈培辉, 王晓鸣. 弹体斜侵彻混凝土靶面的开坑阶段分析 [J]. 南京理工大学学报, 2016, 40(1): 72–76.XUE Jianfeng, SHEN Peihui, WANG Xiaoming. Analysis on crater-forming of projectile obliquely penetrating into concrete target [J]. Journal of Nanjing University Science Technology, 2016, 40(1): 72–76. [13] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. doi: 10.1016/0734-743X(94)80024-4 [14] DANCYGIER A N. Rear face damage of normal and high-strength concrete elements caused by hard projectile impact [J]. Aci Structural Journal, 1998, 95(3): 291–304. [15] HANCHAK S J, FORRESTAL M J, YOUNG E R, et al. Perforation of concrete slabs with 48 MPa (7 ksi) and 140 MPa (20 ksi) unconfined compressive strengths [J]. International Journal of Impact Engineering, 1992, 12(1): 1–7. doi: 10.1016/0734-743X(92)90282-X -
计量
- 文章访问数: 6342
- HTML全文浏览量: 2088
- PDF下载量: 104
- 被引次数: 0