Attenuation of blast wave in a large-section tunnel
-
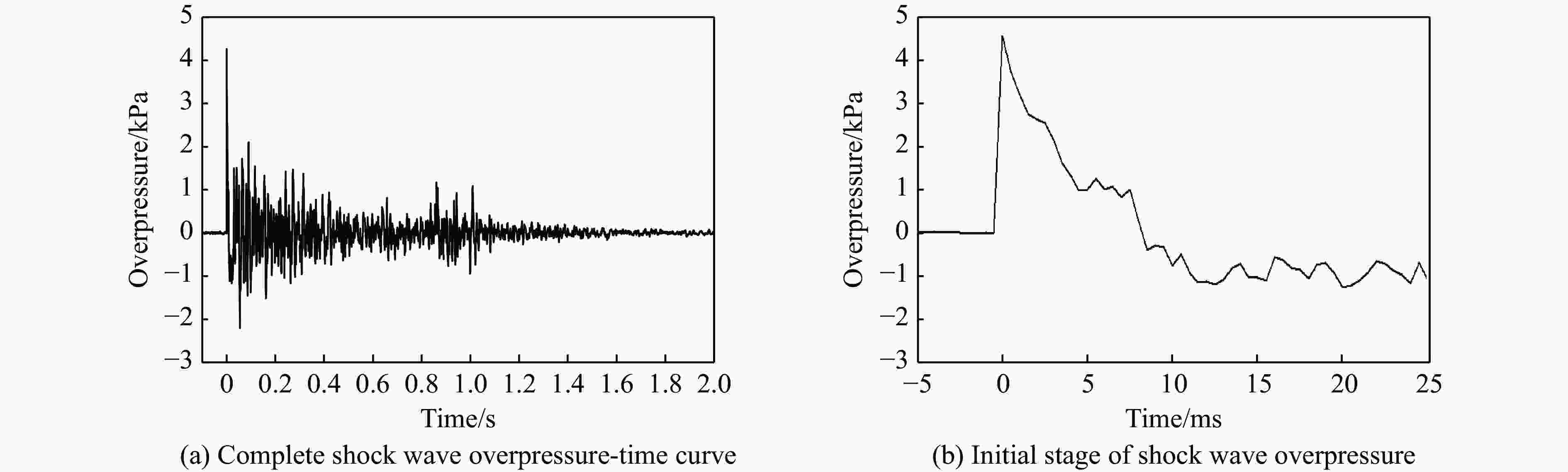
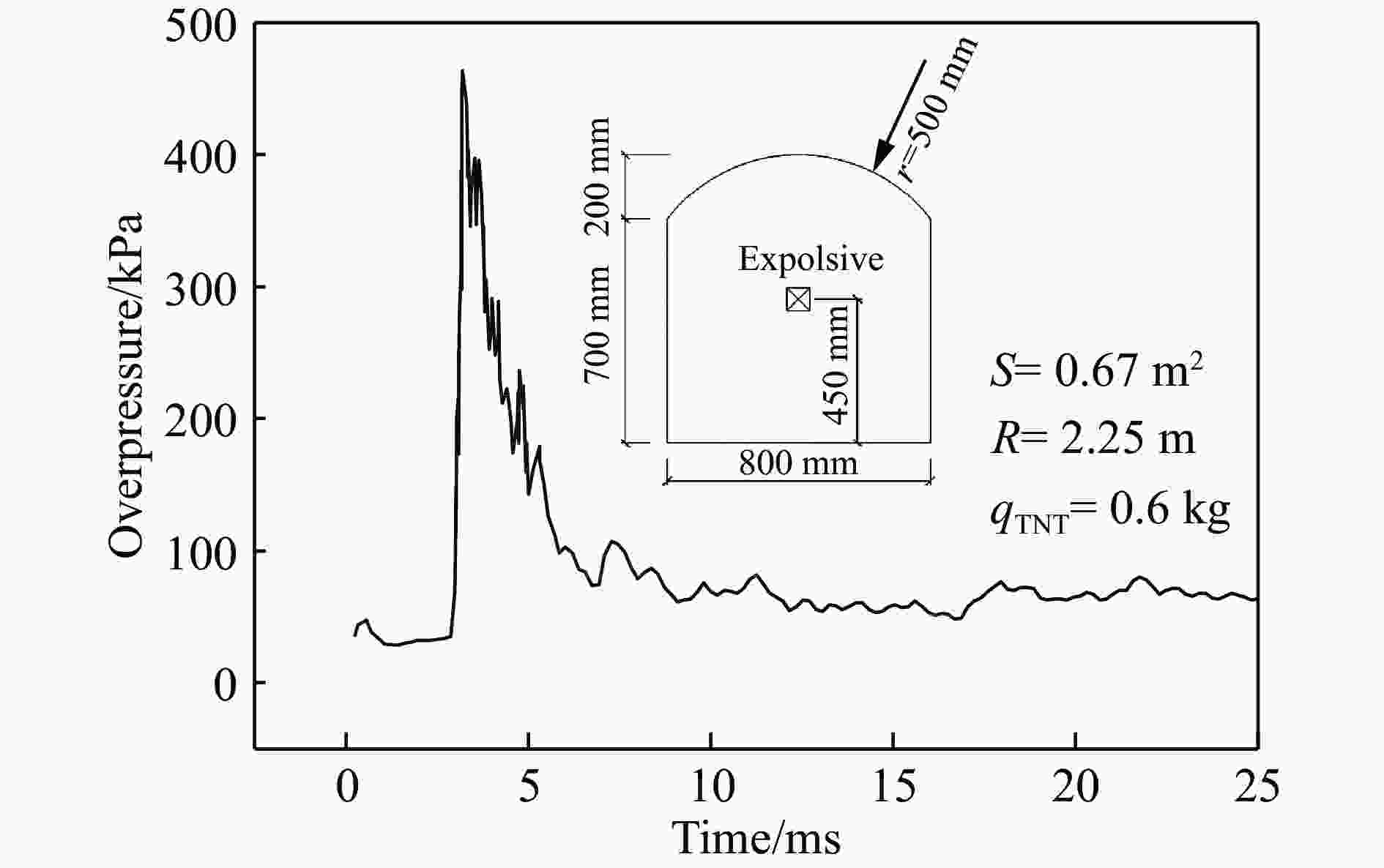
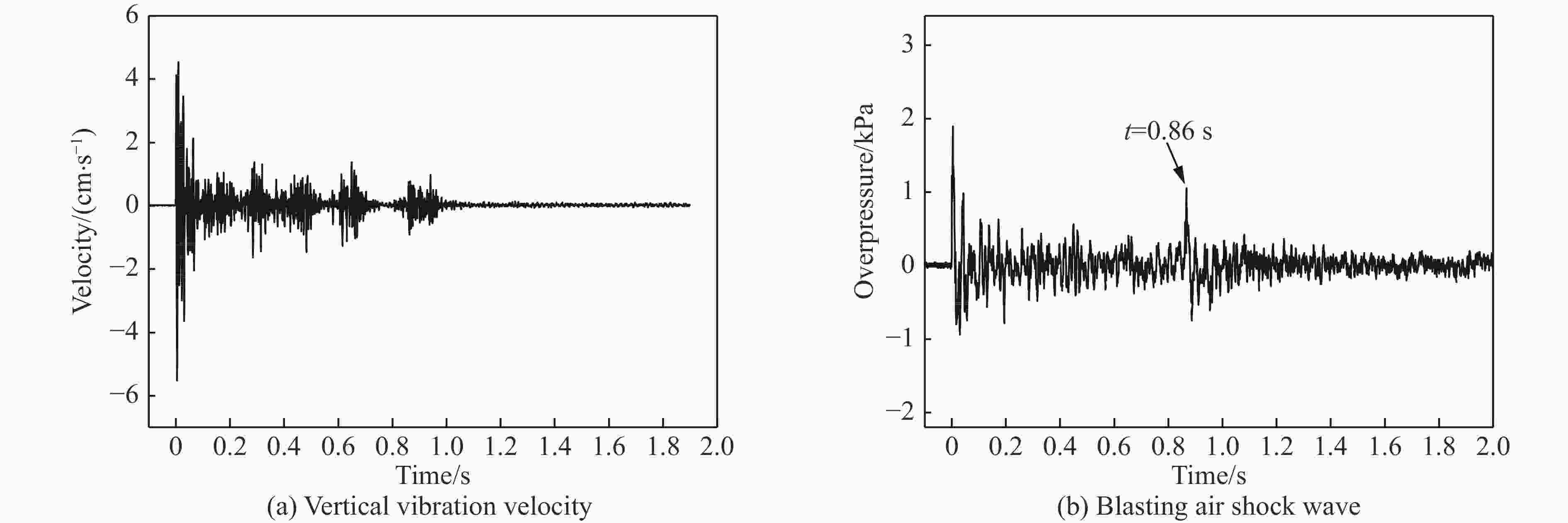
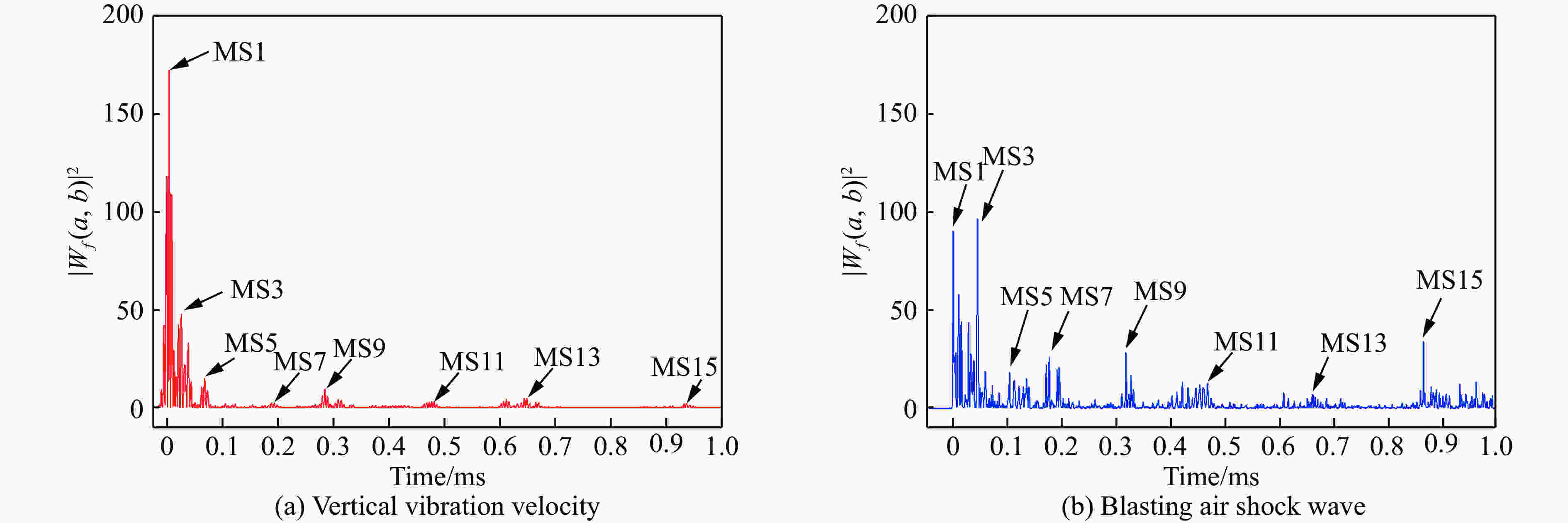
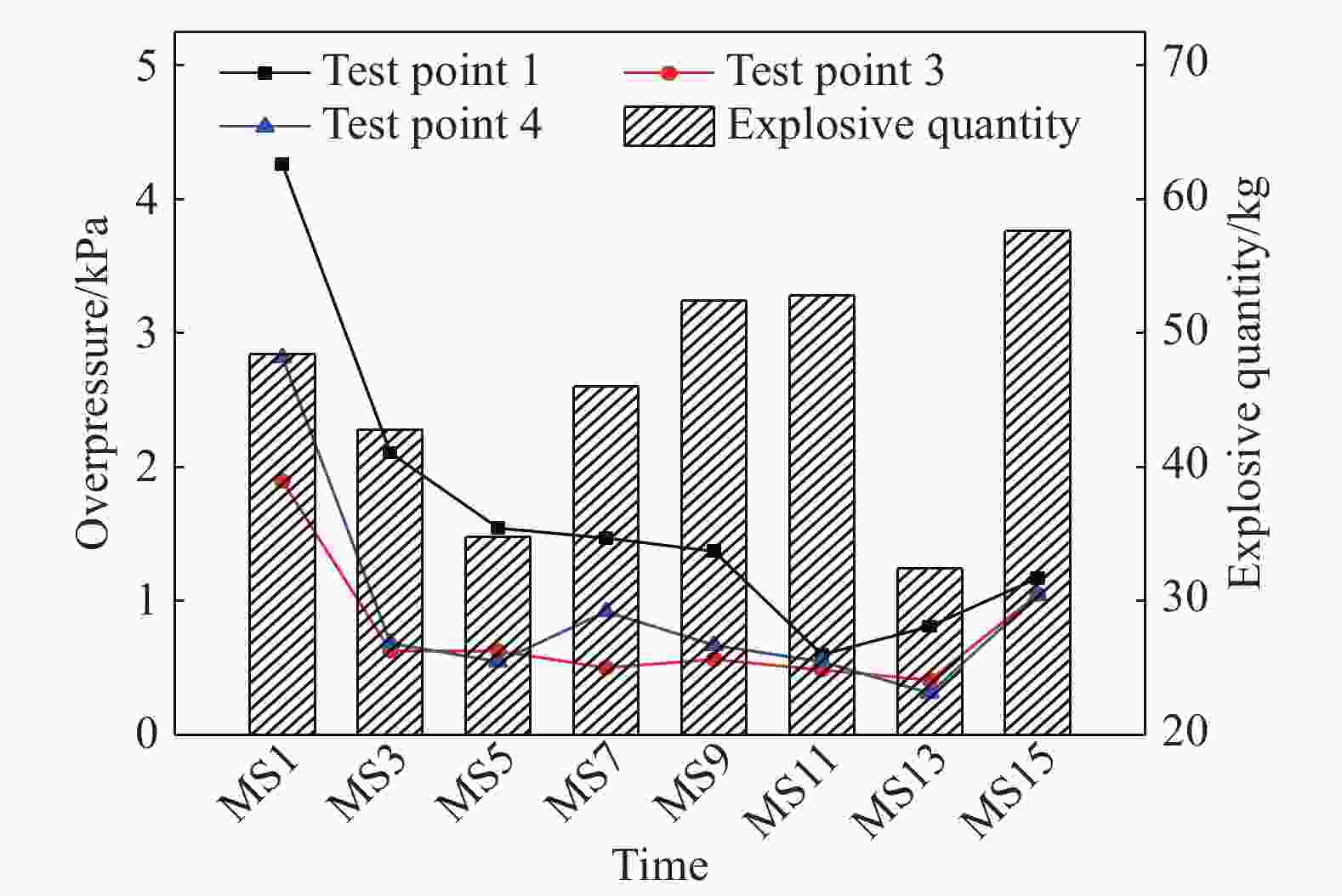
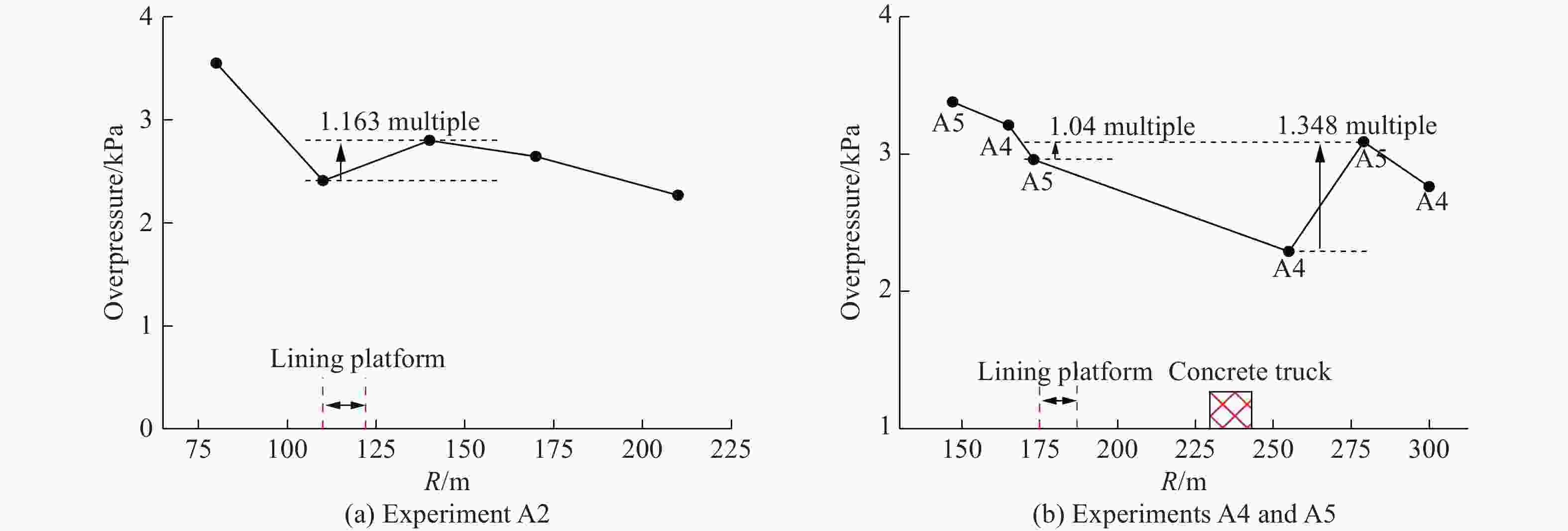
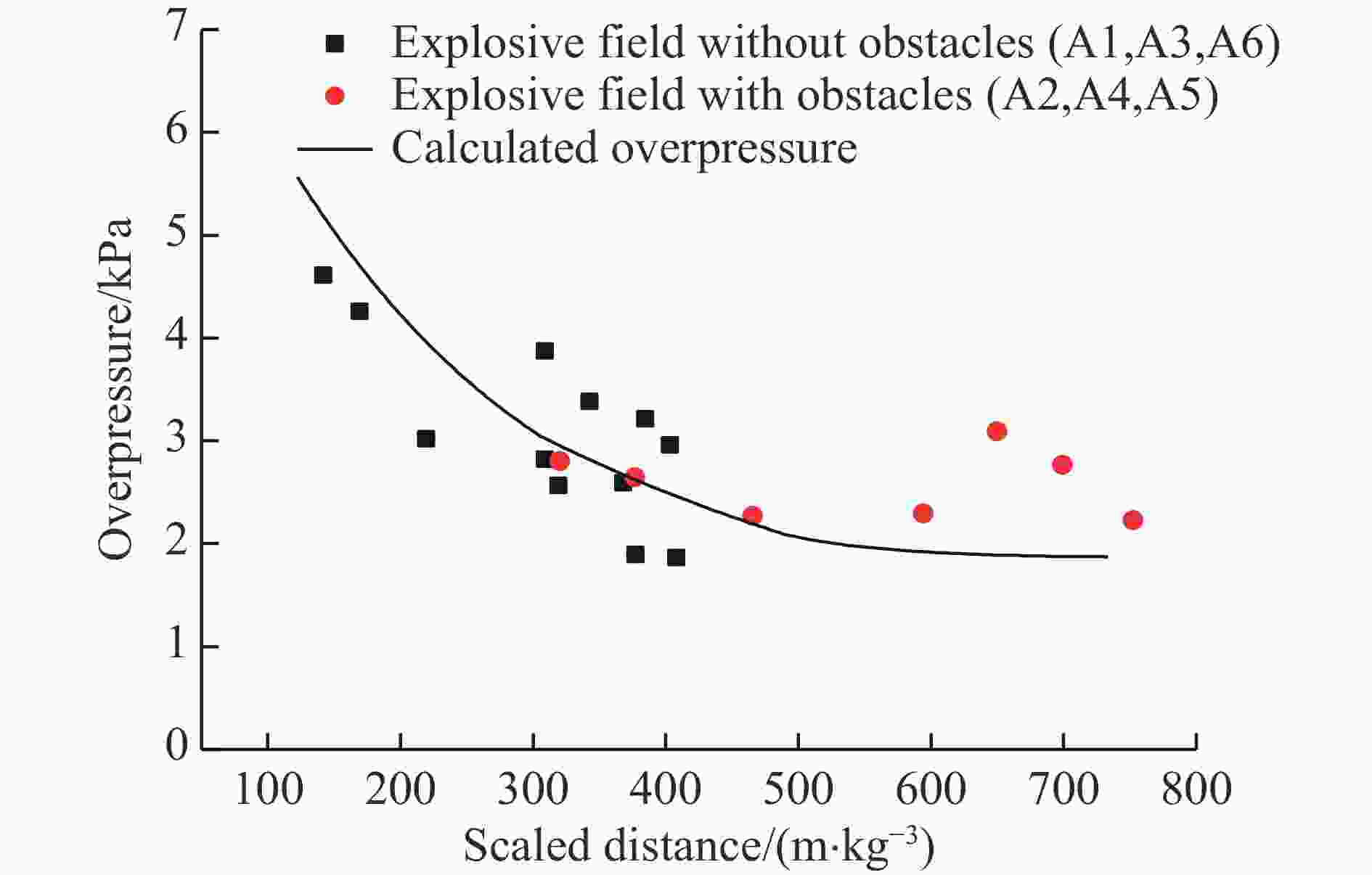
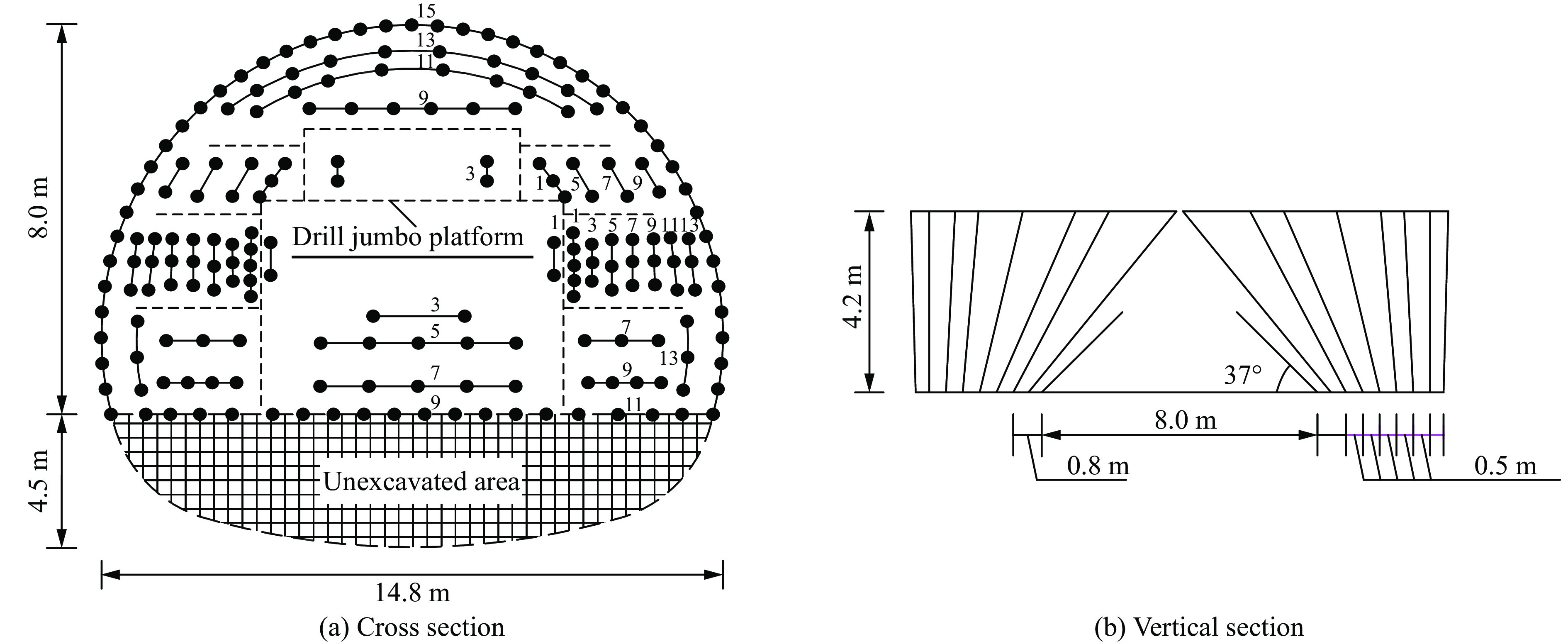
摘要: 隧道开挖爆破产生的空气冲击波的破坏效应,将会对人员、机具设备与周围环境造成危害。隧道钻孔爆破冲击波的影响因素比裸露药包爆炸更多、更复杂,研究其衰减规律对采取合适的防护措施意义重大。本文中开展了时速350 km双线铁路大断面隧道钻孔爆破空气冲击波的现场测试,分析了不同工况下冲击波传播规律及影响因素。结果表明:钻爆冲击波超压时程曲线存在多个不同幅值的超压波峰,波峰之间具有明显微差延时的短间隔性,传播至远场未形成稳定的单一平面波,与单一药包爆炸冲击波的传播规律存在差异;钻爆冲击波超压信号由多段与微差延时相对应的子信号叠加而成,子信号数量与毫秒延期雷管段数相同,呈现出典型的时域特征;相同爆破条件下,大断面隧道钻爆时的乳化炸药冲击波转化因数小于小断面巷道工况下的;相较于总药量及最大段药量,按掏槽药量计算的超压峰值与实测超压峰值之间的相关性最强,钻爆冲击波最大超压峰值宜按掏槽段炸药TNT当量确定;隧道内大型机械设备等障碍物改变了钻爆冲击波流场的传播规律,呈现较明显的叠加放大效应。Abstract: The blasting air shock wave produced by tunnel excavation results in considerable casualties and damage to equipments and environments. Compared with those of the explosion of bare charges, the influencing factors of the blast wave induced by tunnel drilling are more complicated, so it is of considerable significance to study its attenuation law for taking appropriate protective measures. In this paper, a field test of blasting shock wave was carried out during the drilling and blasting of a large cross-section tunnel with a speed of 350 km/h, and the propagation law and influence factors of blasting shock wave under different conditions were analyzed. The results display that there are multiple overpressure peaks with different amplitudes in the shock wave overpressure-time curve, showing the short time intervals with significant millisecond delay characteristics between wave peaks. When the shock wave propagates to the far field, it does not form a stable plane wave, and it is different from the propagation law of shock wave of the single charge explosion. The shock wave overpressure signal is superimposed by multiple sub-signals, showing typical time domain properties, and the number of sub-signals is the same as that of the millisecond delay detonator segments. Under the same blasting conditions, the conversion factor of emulsion explosive energy into shock wave in a large-section tunnel is smaller than that in a small-section tunnel. Compared with the total charge and the maximum charge, the linear correlation between the peak values of shock wave overpressure calculated by the cut-hole charge and the measured peak values is the strongest. Then the maximum peak value of the blasting shock wave overpressure should be determined according to TNT equivalent of the cut-hole charge. Obstacles such as the large equipment in the tunnel will change the propagation law of the shock wave, showing a significant superimposed amplification effect.
-
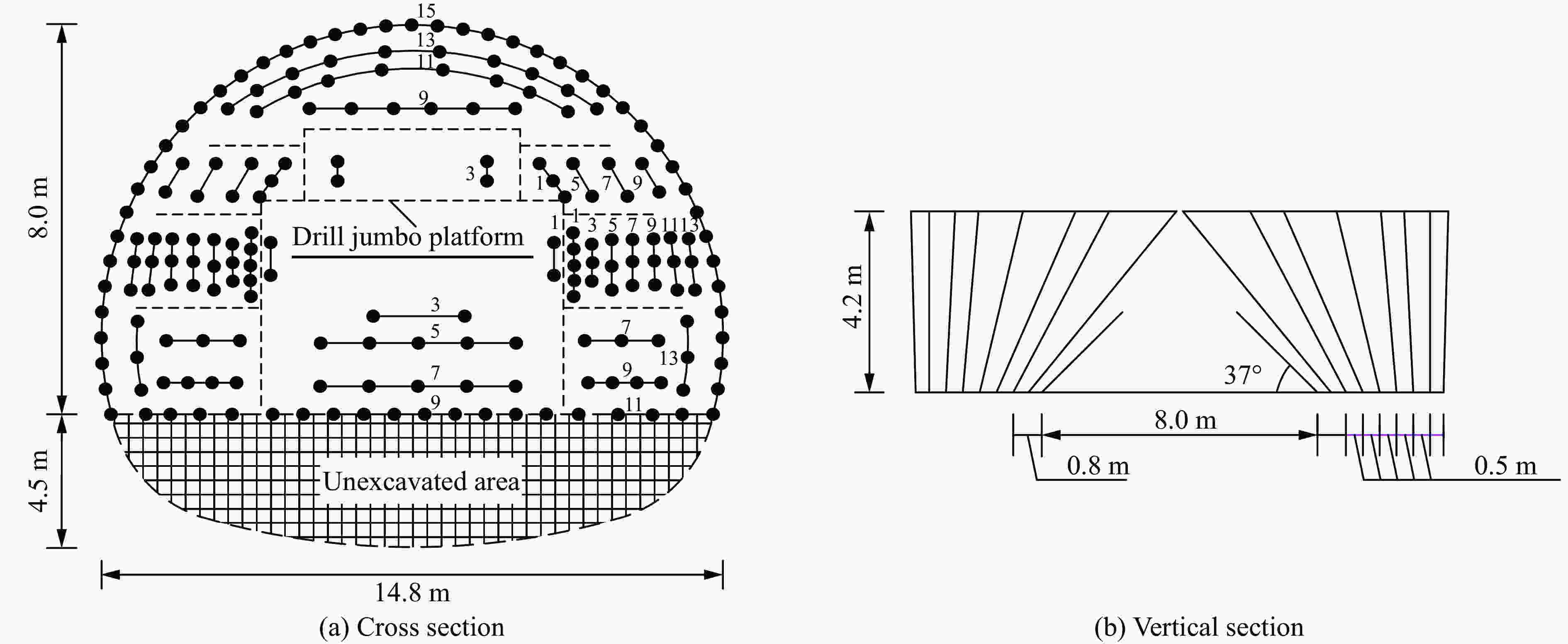
表 1 上台阶钻爆设计参数
Table 1. Design parameters of borehole blasting for the upper bench
炮孔分类 段别 孔数 孔深/m 单孔药卷数 单孔用药量/kg 延期时间/ms 总药量/kg 内掏槽 1 4 3.0 5 1.0 0 4.0 外掏槽 1 16 5.5 12/15 2.4/3.0 0 44.4 辅助孔 3 16 4.8 13 2.6 50 41.6 辅助孔 5 10 4.8 12 2.4 110 24.0 辅助孔 7 12 4.5 11 2.2 200 26.4 辅助孔 9 18 4.5 11 2.2 310 39.6 辅助孔 11 6 4.3 11 2.2 460 13.2 辅助孔 13 12 4.2 8/9 1.6/1.8 650 20.4 上周边孔 15 47 4.2 4 0.8 880 37.6 下周边孔 15 8 4.2 8/9/10/11 1.6/1.8/2.0/2.2 880 15.2 压孔 7 6 4.5 8 1.6 200 9.6 压孔辅助 9 8 4.5 8 1.6 310 12.8 二圈孔 13 10 4.2 6 1.2 650 12.0 抬孔 3 2 4.3 3 0.6 50 1.2 抬孔 5 6 4.2 9 1.8 110 10.8 抬孔 7 5 4.2 10 2.0 200 10.0 底板孔 11 16 4.5 8/11/12 1.6/2.2/2.4 460 39.6 角孔 15 2 4.5 12 2.4 880 4.8 合计 367.2 表 2 隧道上台阶钻爆冲击波测试结果
Table 2. Records of shock wave test in upper bench cutting
试验工况 总药量/kg 掏槽药量/kg 最大段药量(段别)/kg 测点 爆心距/m 超压峰值/kPa A1 367.2 48.4 57.6 (MS15) 1 74.5 4.259 3 136.0 2.818 4 166.0 1.894 A2 359.5 49.6 90.4 (MS09) 1 80.0 3.549 2 110.0 2.408 3 140.0 2.802* 4 170.0 2.645* 5 210.0 2.269* A3 359.5 49.6 90.4 (MS09) 1 64.0 4.608 2 99.0 3.019 3 144.0 2.567 4 184.0 1.863 A4 343.7 47.2 62.4 (MS11) 1 165.0 3.213 3 255.0 2.292* 4 300.0 2.764* A5 343.7 47.2 62.4 (MS11) 1 147.0 3.380 2 173.0 2.959 3 279.0 3.089* A6 351.7 52.0 63.2 (MS11) 1 146.0 3.870 2 174.0 2.590 -
[1] BENSELAMA A M, WILLIAM-LOUIS MAMEJ P, MONNOYER F, et al. A numerical study of the evolution of the blast wave shape in tunnels [J]. Journal of Hazardous Materials, 2010, 181(1-3): 609–616. DOI: 10.1016/j.jhazmat.2010.05.056. [2] 杨科之, 杨秀敏. 坑道内化爆冲击波的传播规律 [J]. 爆炸与冲击, 2003, 23(1): 37–40.YANG K Z, YANG X M. Shock waves propagation inside tunnels [J]. Explosion and Shock Waves, 2003, 23(1): 37–40. [3] 李秀地, 郑颖人. 坑道中冲击波冲量传播模型的试验 [J]. 解放军理工大学学报(自然科学版), 2007, 8(5): 425–428. DOI: 10.7666/j.issn.1009-3443.20070504.LI X D, ZHENG Y R. Scale model tests to determine in tunnel blast impulse from HE charges at tunnel entrance [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2007, 8(5): 425–428. DOI: 10.7666/j.issn.1009-3443.20070504. [4] 刘晶波, 闫秋实, 伍俊. 坑道内爆炸冲击波传播规律的研究 [J]. 振动与冲击, 2009, 28(6): 8–11. DOI: 10.3969/j.issn.1000-3835.2009.06.003.LIU J B, YAN Q S, WU J. Analysis of blast wave propagation inside tunnels [J]. Journal of Vibration and Shock, 2009, 28(6): 8–11. DOI: 10.3969/j.issn.1000-3835.2009.06.003. [5] 田志敏, 邬玉斌, 罗奇峰. 隧道内爆炸冲击波传播特性及爆炸荷载分布规律研究 [J]. 振动与冲击, 2011, 30(1): 21–26. DOI: 10.3969/j.issn.1000-3835.2011.01.005.TIAN Z M, WU Y B, LUO Q F. Characteristics of in-tunnel explosion-induced air shock wave and distribution law of reflected shock wave load [J]. Journal of Vibration and Shock, 2011, 30(1): 21–26. DOI: 10.3969/j.issn.1000-3835.2011.01.005. [6] YAN Q S, DU X L. Forecasting research of overpressure of explosive blast in subway tunnels [J]. Journal of Vibroengineering, 2015, 17(6): 33810–3391. [7] 李玉民, 胡峰. 井下爆破空气冲击波传播规律的量纲分析与拟合 [J]. 矿冶工程, 1993, 13(2): 13–17.LI Y M, HU F. The dimensional and regression analyses on the propagation regulation of air blast waves in mines [J]. Mining and Metallurgical Engineering, 1993, 13(2): 13–17. [8] 庞伟宾, 何翔, 李茂生, 等. 空气冲击波在坑道内走时规律的实验研究 [J]. 爆炸与冲击, 2003, 23(6): 573–576.PANG W B, HE X, LI M S, et al. The formula for air blast time of arrival in tunnel [J]. Explosion and Shock Waves, 2003, 23(6): 573–576. [9] 庞伟宾, 李永池, 何翔. 化爆冲击波在T型通道内到时规律的实验研究 [J]. 爆炸与冲击, 2007, 27(1): 63–67. DOI: 10.11883/1001-1455(2007)01-0063-05.PANG W B, LI Y C, HE X. The regularity of arrival time in T-shaped tunnel for shock wave due to explosions from high explosive charges [J]. Explosion and Shock Waves, 2007, 27(1): 63–67. DOI: 10.11883/1001-1455(2007)01-0063-05. [10] 赵晓磊. 城市地铁浅埋隧道爆破振动及空气冲击波传播规律探索[D]. 大连: 大连理工大学, 2015.ZHAO X L. Exploration of laws of blasting vibration and air blast propagation for urban shallow tunnels [D]. Dalian, China: Dalian University of Technology, 2015. [11] 陈明, 何文学, 卢文波, 等. 隧洞开挖爆破空气超压诱发围岩振动机理 [J]. 振动与冲击, 2017, 36(12): 12–17. DOI: 10.13465/j.cnki.jvs.2017.12.003.CHEN M, HE W X, LU W B, et al. Studies on the vibration of tunnel surrounding rock induced by air overpressure [J]. Journal of Vibration and Shock, 2017, 36(12): 12–17. DOI: 10.13465/j.cnki.jvs.2017.12.003. [12] 汪旭光, 于亚伦, 刘殿中. 爆破安全规程实施手册[M]. 北京: 人民交通出版社, 2004: 157−158. [13] 张胜, 凌同华, 刘浩然, 等. 模式自适应小波时能密度法及其在微差爆破振动信号分析中的应用 [J]. 煤炭学报, 2014, 39(10): 2007–2013. DOI: 10.13225/j.cnki.jccs.2014.0325.ZHANG S, LING T H, LIU H R, et al. Pattern adapted wavelet time-energy density method and its application in millisecond blast vibration signal analysis [J]. Journal of China Coal Society, 2014, 39(10): 2007–2013. DOI: 10.13225/j.cnki.jccs.2014.0325. [14] 汪旭光, 郑炳旭, 张正忠, 等. 爆破安全规程GB6722-2014 [S]. 北京: 中国标准出版社, 2015: 42−46. [15] 萨文科, 古林, 马雷. 井下空气冲击波[M]. 龙维祺, 丁亚伦, 译. 北京: 冶金工业出版社, 1979: 98−100. -






 下载:
下载: