W/ZrNiAlCu亚稳态合金复合材料破片对RHA靶的侵彻释能特性

张云峰; 罗兴柏; 刘国庆; 施冬梅; 张玉令; 甄建伟

doi:10.11883/bzycj-2019-0065

W/ZrNiAlCu亚稳态合金复合材料破片对RHA靶的侵彻释能特性

doi: 10.11883/bzycj-2019-0065

陆军工程大学石家庄校区，河北石家庄 050000

详细信息

作者简介:
张云峰（1990－　），男，博士研究生，1193954881@qq.com

通讯作者:
刘国庆（1975－　），男，博士，副教授，13081106809@163.com

中图分类号: O385; TJ410
计量
- 文章访问数: 5941
- HTML全文浏览量: 1585
- PDF下载量: 61
- 被引次数: 0
出版历程
- 收稿日期: 2019-03-04
- 修回日期: 2019-04-26
- 网络出版日期: 2020-01-25
- 刊出日期: 2020-02-01

Penetration and energy release effect of W/ZrNiAlCu metastable reactive alloy composite rragment against RHA target

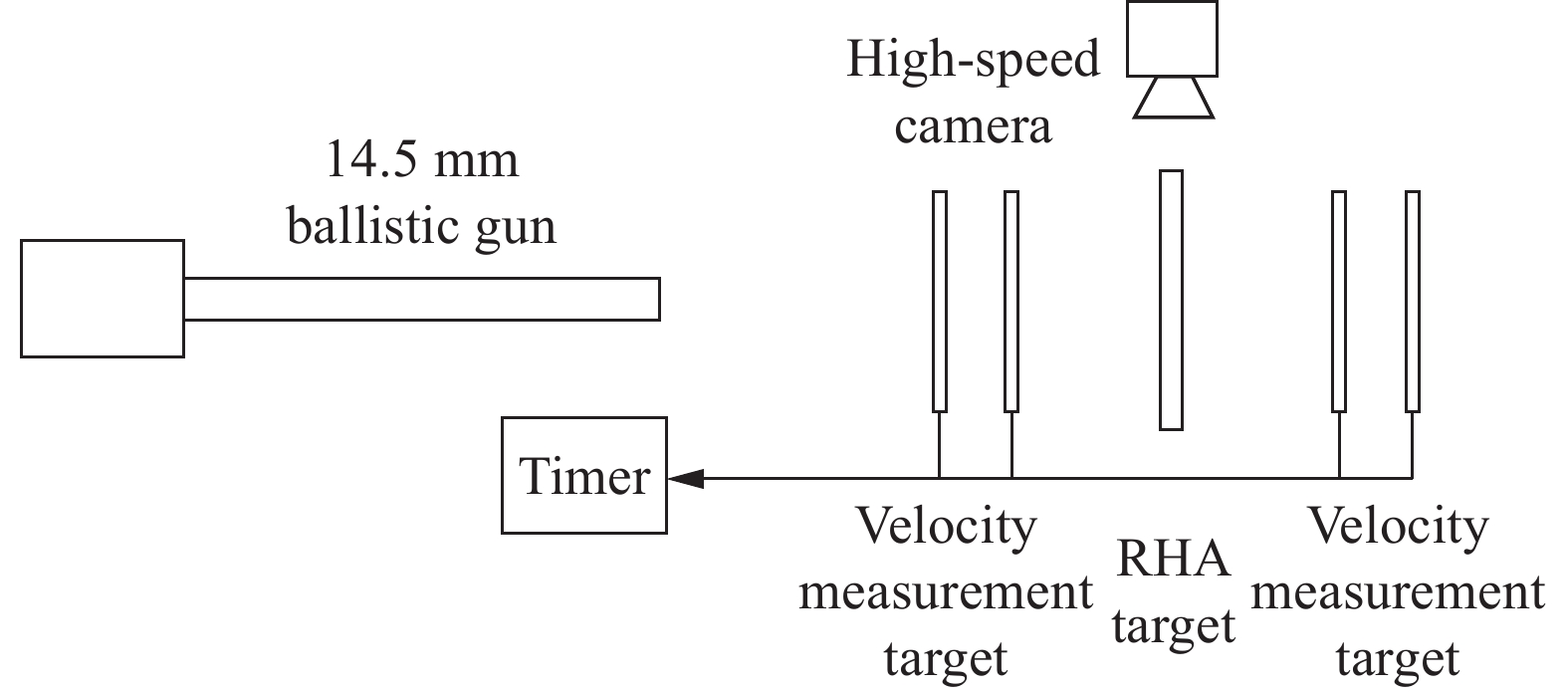
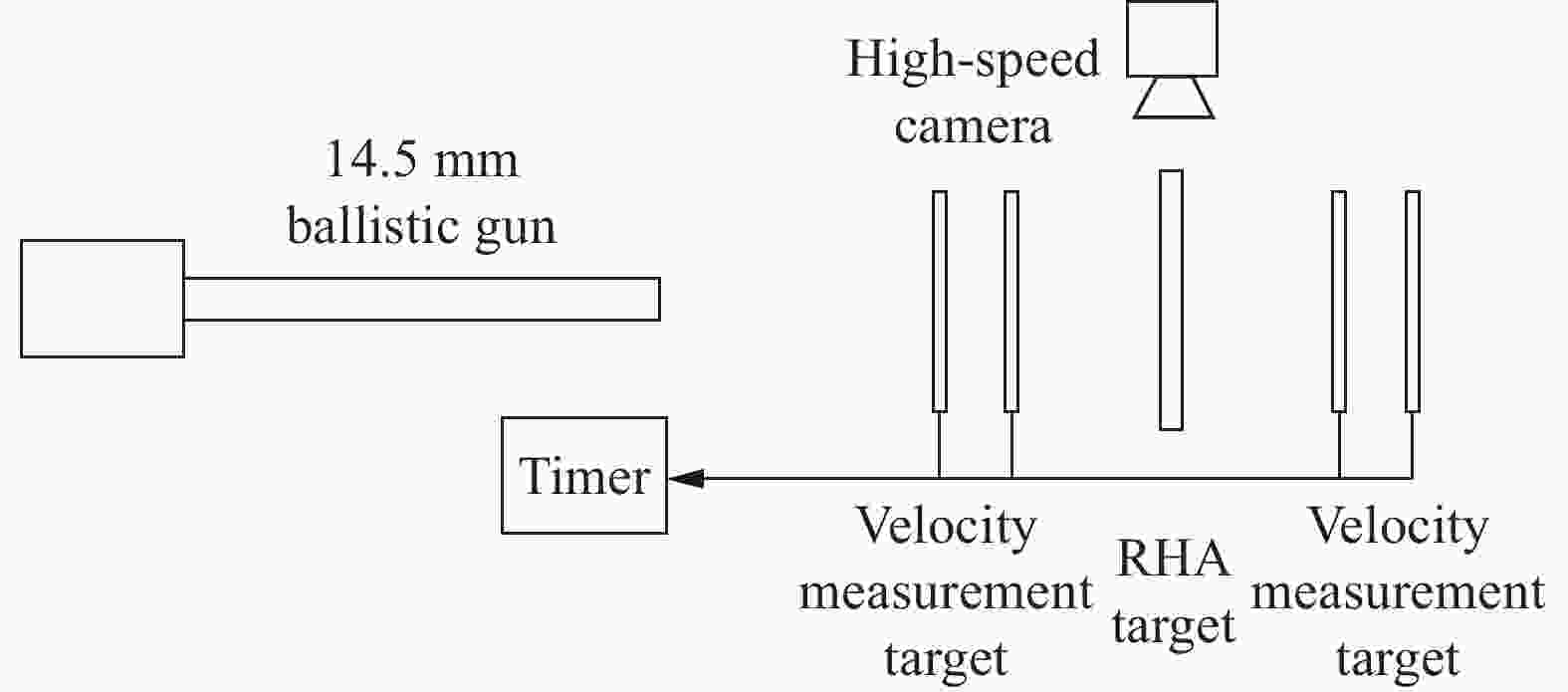
Shijiazhuang College, Army Engineering University, Shijiazhuang 050000, Hebei, China

摘要

摘要: 为研究W/ZrNiAlCu亚稳态合金复合材料破片对RHA靶板的侵彻释能特性，采用高速摄影弹道枪侵彻实验和能量方程、Avrami-Erofeev方程理论分析的方法，对破片的侵彻释能过程、侵彻规律、释能规律进行了研究。结果表明，破片在撞击并贯穿靶板的过程中激发了材料的燃烧反应，在靶板前方和后方产生了明显火光，随着撞击速度增加，火光范围增加、亮度提高；破片撞击速度、冲塞体速度的关系符合采用能量法推导的包含质量损失的破片侵彻公式，破片理论弹道极限速度为987.1 m·s⁻¹；在实验速度范围内，材料反应效率随着冲击压力的增加而增加，与实验现象吻合。
- 亚稳态合金复合材料 /
- 侵彻规律 /
- 释能特性 /
- RHA靶
Abstract: To study the penetration and energy release effect of W/ZrNiAlCu metastable reactive alloy composite fragment against RHA target, the penetration tests using high-speed camera and ballistic gun system were conducted. And the energy equation and Arami-Erofeev equation was produced to theoretical analyze the results of penetration tests. The results show that the combustion reaction of fragment is induced by penetration process, which initiates distinct flame in the front of the target and behind the target. The brightness and scope of flame are enhanced with the increase of impact velocity. The relationship between impact velocity and plug velocity conforms to the penetration equation deduced by energy method. The theoretical ballistic limit velocity is 987.1 m/s. The efficiency of reaction is enhanced with the increase of impact pressure within the experimental velocities, which consistent with the experiment.
- metastablereactive alloy composite /
- penetration characters /
- energy release characters /
- RHA target

HTML全文

图 1 侵彻实验装置布置

Figure 1. Layout of penetration experimental setup

下载: 全尺寸图片幻灯片

图 2 不同撞击速度下W/ZrNiAlCu亚稳态合金复合材料破片对RHA靶板的侵彻释能过程

Figure 2. Penetration and energy release processes of W/ZrNiAlCu metastable reactive alloy composite fragments against RHA targets at different impact velocities

下载: 全尺寸图片幻灯片

图 3 v_i-v_p关系曲线

Figure 3. Curve of v_i-v_p relationship

下载: 全尺寸图片幻灯片

图 4 冲击压力与反应效率的理论曲线

Figure 4. Theoretical curve of reaction efficiencyversus shock pressure

下载: 全尺寸图片幻灯片

表 1 破片侵彻实验结果

Table 1. Experimental results of fragments penetration

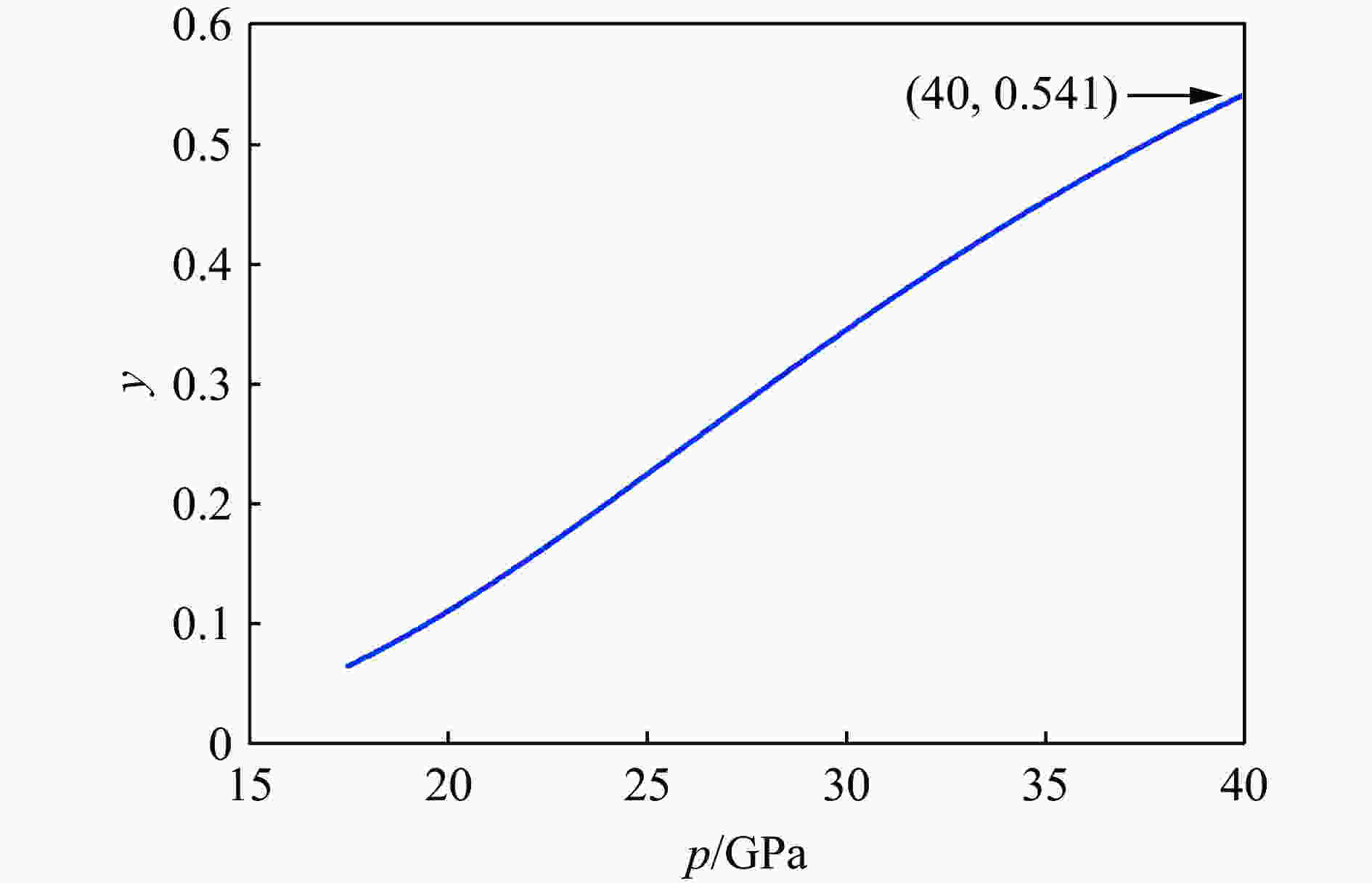
编号	m/g	v_i/(m·s⁻¹)	v_p/(m·s⁻¹)	p/GPa	是否穿透
1#	6.65	726	−	16.46	否
2#	6.54	810	−	18.63	否
3#	6.39	995	−	23.62	否
4#	6.68	973	34	23.01	是
5#	6.80	1 067	137	25.63	是
6#	6.72	1 144	176	27.83	是
7#	6.37	1 159	131	28.26	是
8#	6.65	1 240	195	30.64	是
9#	6.51	1 295	317	32.28	是
10#	6.56	1 359	397	34.21	是
11#	6.68	1 508	497	38.85	是

下载: 导出CSV

表 2 W/ZrNiAlCu亚稳态合金复合材料参数^[13]

Table 2. Parameters of W/ZrNiAlCu metastable reactive alloy composite

材料	C₀/(m∙s⁻¹)	s	γ_0K	α_V/(10⁻⁵·K⁻¹)	C_V/(J·g⁻¹·K⁻¹)	E_a/(kJ·mol⁻¹)	n
W/ZrNiAlCu	3 417	1.732	1.629	1.559	0.182	459.25	0.347

下载: 导出CSV

参考文献(13)

[1]	张先锋, 赵晓宁. 多功能含能结构材料研究进展 [J]. 含能材料, 2009, 17(6): 731–739. DOI: 10.3969/jissn.1006-9941.2009.06.021. ZHANG X F, ZHAO X N. Review on multifunctional energetic structural materials [J]. Chinese Journal of Energetic Materials, 2009, 17(6): 731–739. DOI: 10.3969/jissn.1006-9941.2009.06.021.
[2]	XU F Y, ZHENG Y F, YU Q B, et al. Experimental study on penetration behavior of reactive material projectile impacting aluminum plate [J]. International Journal of Impact Engineering, 2016, 95: 125–132. DOI: 10.1016/j.ijimpeng.2016.05.007.
[3]	ZHANG X F, SHI A S, QIAO L, et al. Experimental study on impact-initiated characters of multifunctional energetic structural materials [J]. Journal of Applied Physics, 2013, 113: 083508. DOI: 10.1063/1.4793281.
[4]	ZHANG X F, SHI A S, ZHANG J, et al. Thermochemical modeling of temperature controlled shock-induced chemical reactions in multifunctional energetic structural materials under shock compression [J]. Journal of Applied Physics, 2012, 111: 123501. DOI: 10.1063/1.4729048.
[5]	XIONG W, ZHANG X F, WU Y, et al. Influence of additives on microstructures, mechanical properties and shock-induced reaction characteristics of Al/Ni composites [J]. Journal of Alloys and Compounds, 2015, 648: 540–549. DOI: 10.1016/j.jallcom.2015.07.004.
[6]	XIONG W, ZHANG X F, TAN M T, et al. The energy release characteristics of shock-induced chemical reaction of Al/Ni composites [J]. The Journal of Physical Chemistry C, 2016, 120: 24551–24559. DOI: 10.1021/acs.jpcc.6b06530.
[7]	WANG H F, ZHENG Y F, YU Q B. Impact-induced initiation and energy release behavior of reactive materials [J]. Journal of Applied Physics, 2011, 110: 074904. DOI: 10.1063/1.3644974.
[8]	LUO P G, WANG Z C, JIANG C L, et al. Experimental study on impact-initiated characters of W/Zr energetic fragments [J]. Materials and Design, 2015, 84: 72–78. DOI: 10.1016/j.matdes.2015.06.107.
[9]	XU F Y, YU Q B, ZHENG Y F, et al. Damage effects of double-spaced aluminum plates by reactive material projectile impact [J]. International JournalofImpactEngineering, 2017, 104: 13–20. DOI: 10.1016/j.ijimpeng.2017.01.023.
[10]	经福谦. 实验物态方程导引（第二版） [M]. 北京, 科学出版社, 1999: 209−370. JING F Q. Experimental state equation guidance (second edition) [M]. Beijing: Science Press, 1999: 209−370.
[11]	ROSENBERG Z, DEKEL E. 终点弹道学 [M]. 钟方平, 译. 北京: 国防工业出版社, 2014: 120−135.
[12]	谭华. 实验冲击波物理导引[M]. 北京: 国防工业出版社, 2007: 15−61. TAN H. Introduction to experimental shock-wave physics [M]. Beijing: National Defense Industry Press, 2007: 15−61.
[13]	余志统. 钨/多元非晶合金复合材料破片侵彻及冲击释能研究[D]. 石家庄: 陆军工程大学, 2018. YUZ T. Study on penetration and energy release of tungsten/multi-element amorphous alloy composite fragments [D]. Shijiazhuang: Army Engineering University, 2018.