含水率对非饱和钙质砂动力特性影响的试验研究

赵章泳; 邱艳宇; 紫民; 邢化岛; 王明洋

doi:10.11883/bzycj-2019-0066

含水率对非饱和钙质砂动力特性影响的试验研究

doi: 10.11883/bzycj-2019-0066

赵章泳^1,,
邱艳宇^1,2,
紫民³,
邢化岛²,
王明洋^1,2, ,

1.
陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏南京 210007
2.
南京理工大学机械工程学院，江苏南京 210094
3.
海军91058部队，海南三亚 572000

详细信息

作者简介:
赵章泳（1992－　），男，博士研究生，zhaozhangyong1@126.com

通讯作者:
王明洋（1966－　），男，博士，教授，博士生导师，wmyrf@163.com

中图分类号: O341; O344
计量
- 文章访问数: 5794
- HTML全文浏览量: 1697
- PDF下载量: 99
- 被引次数: 0
出版历程
- 收稿日期: 2019-03-04
- 修回日期: 2019-05-23
- 网络出版日期: 2020-01-25
- 刊出日期: 2020-02-01

Experimental study on dynamic compression of unsaturated calcareous sand

1.
State Key Laboratory of Disaster Prevention and Mitigation of Explosion and Impact, the Army Engineering University of PLA, Nanjing 210007, Jiangsu, China
2.
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
3.
Navy 91058 Force, Sanya 572000, Hainan, China

摘要

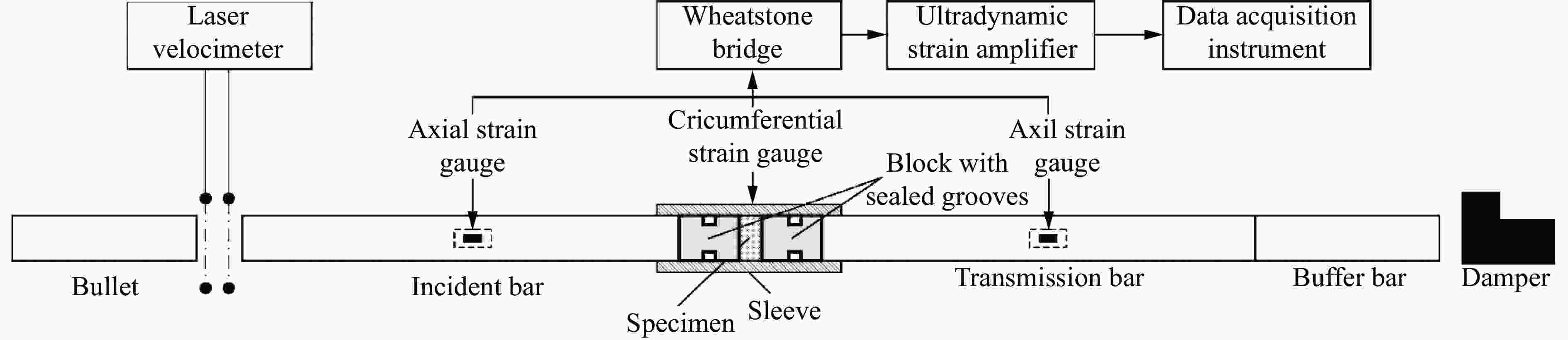
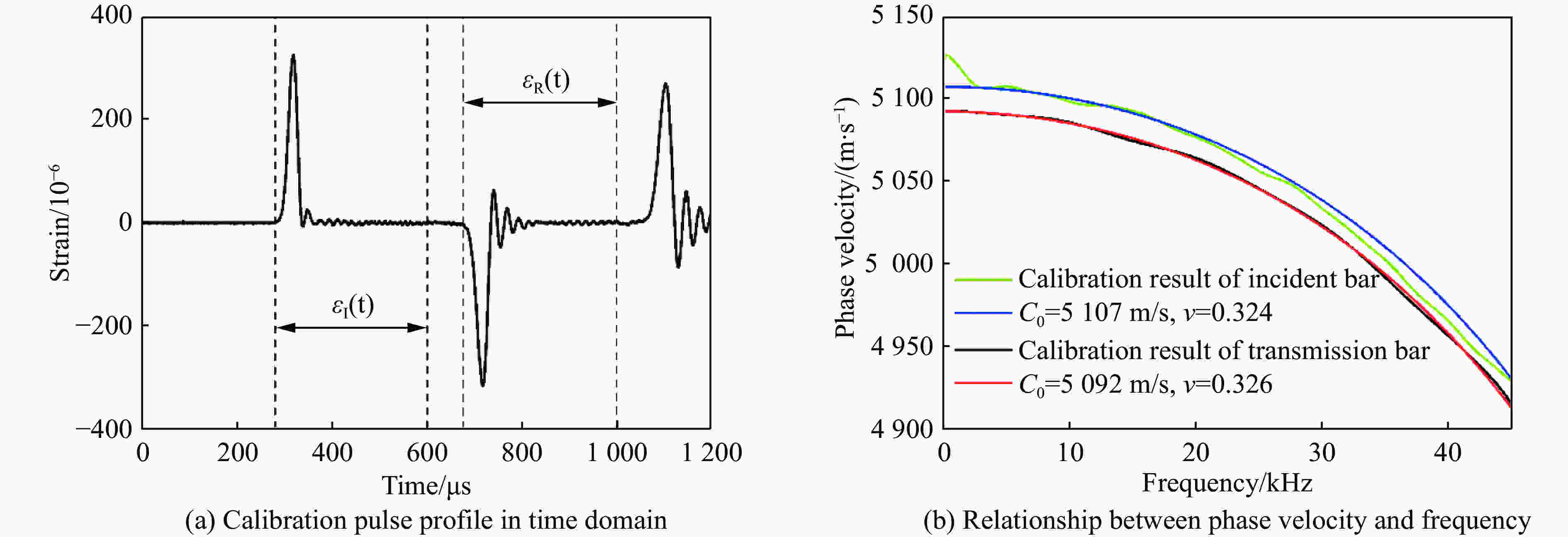
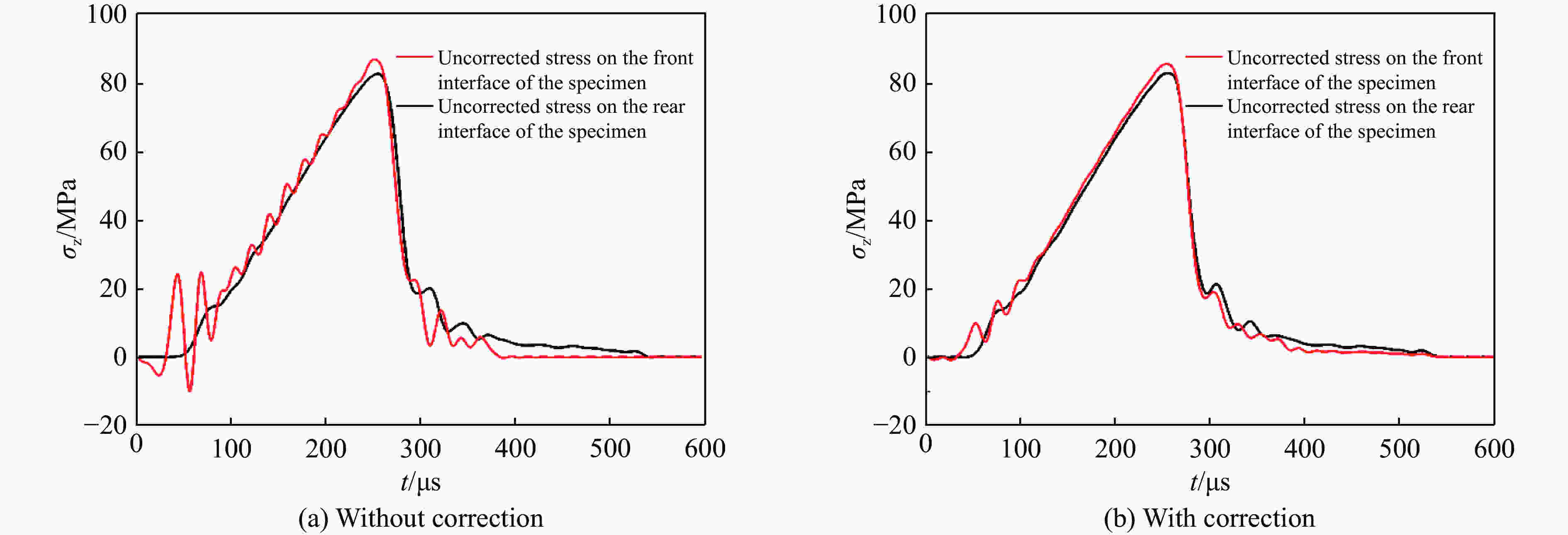
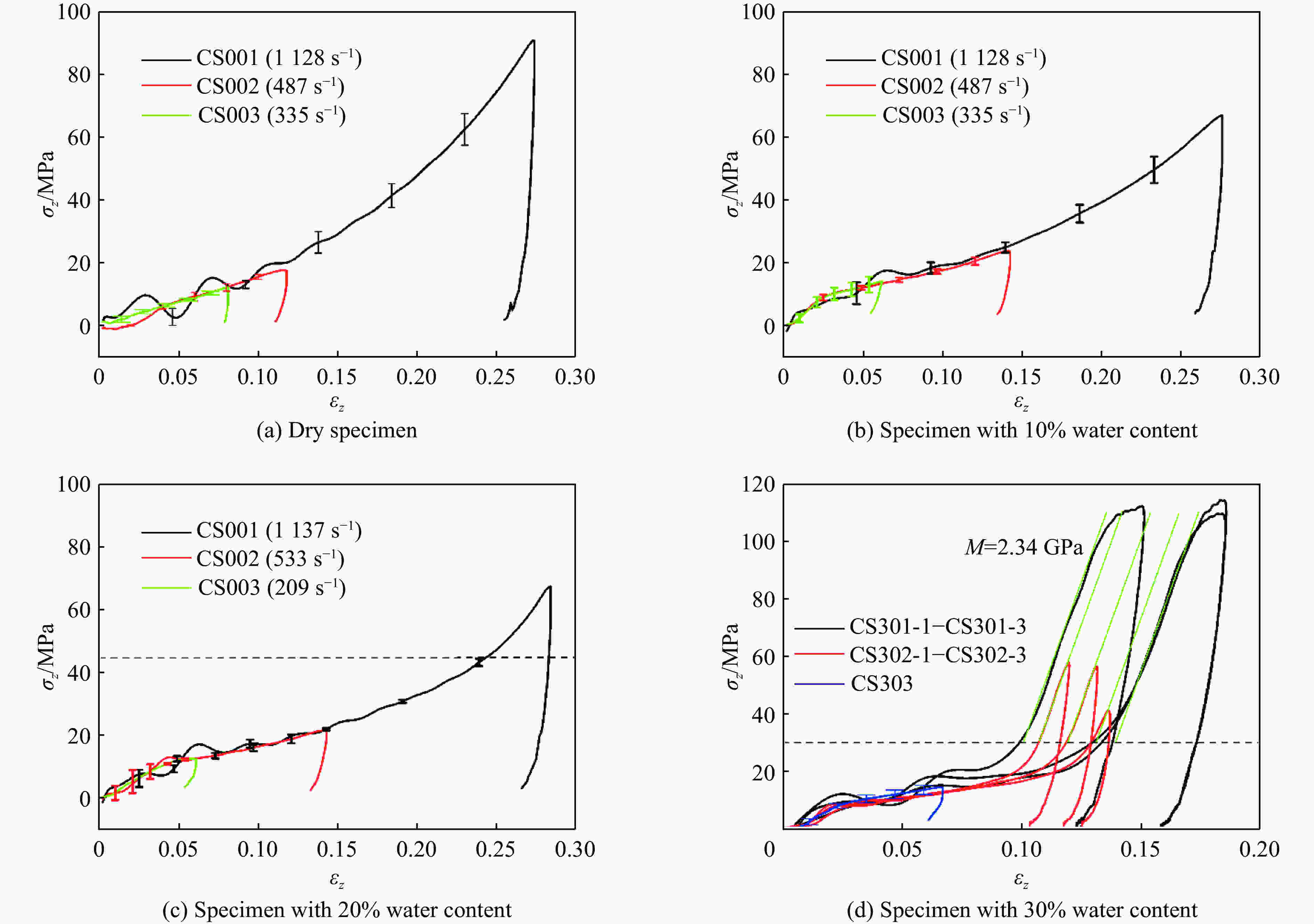
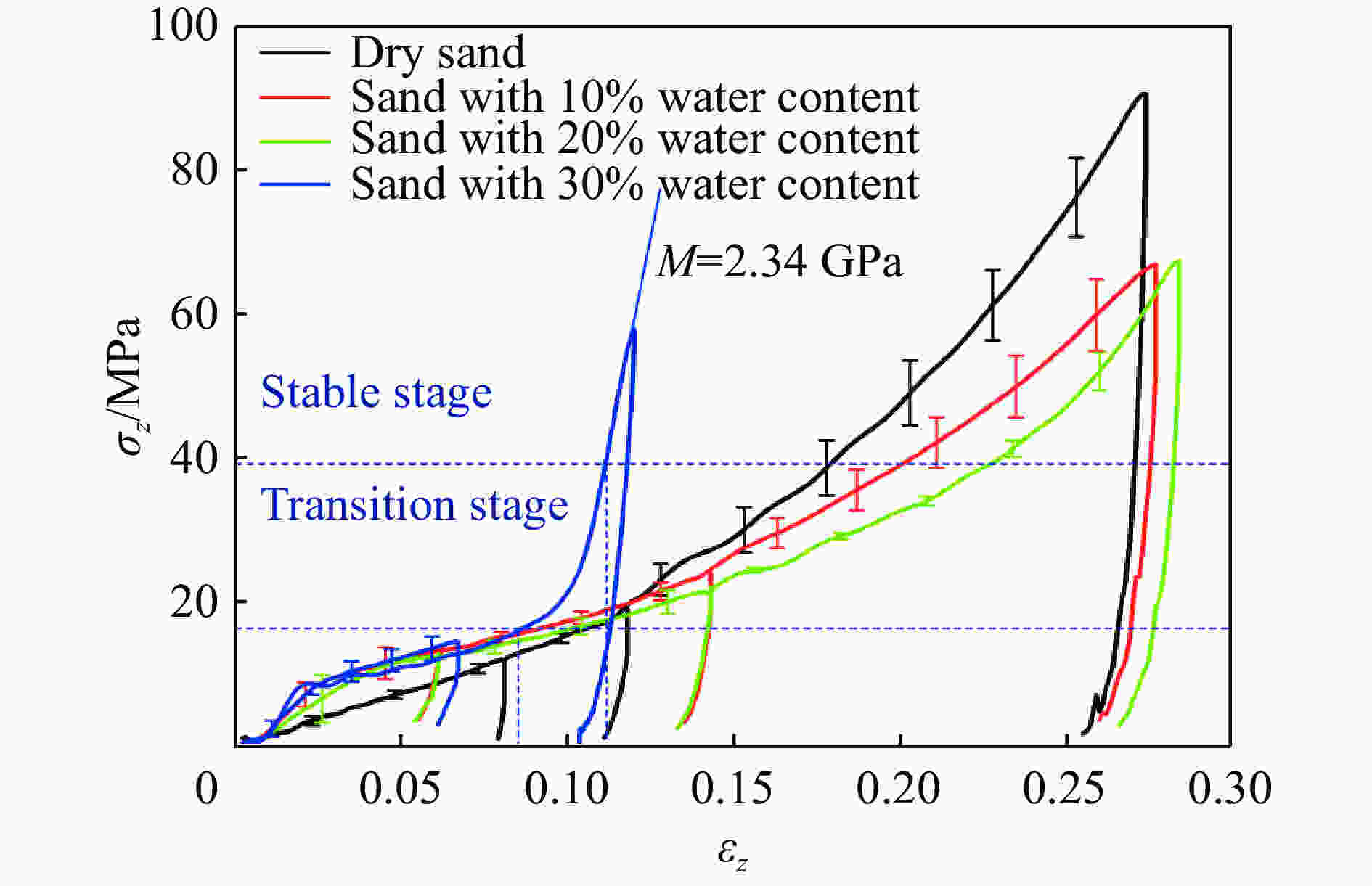
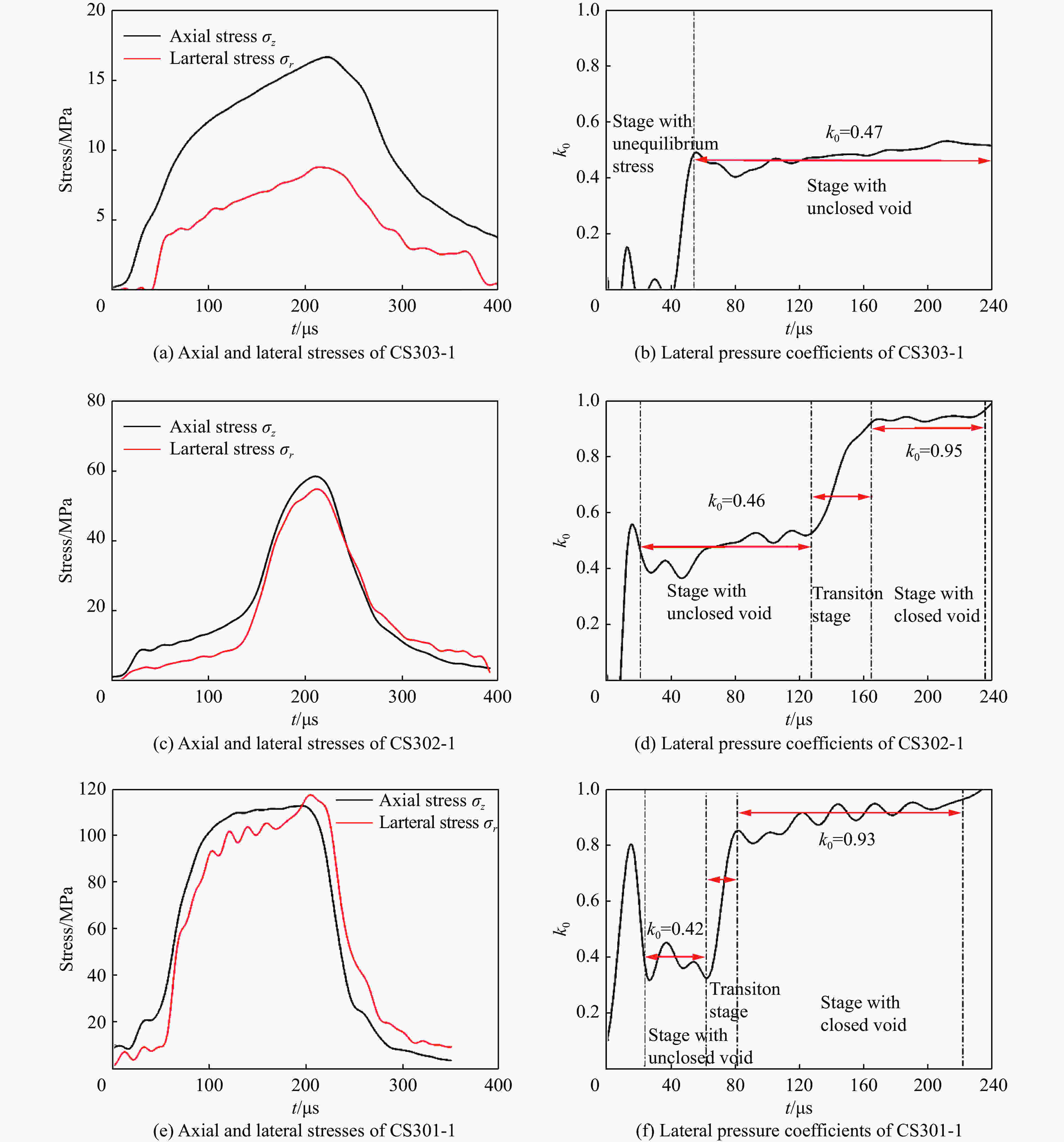
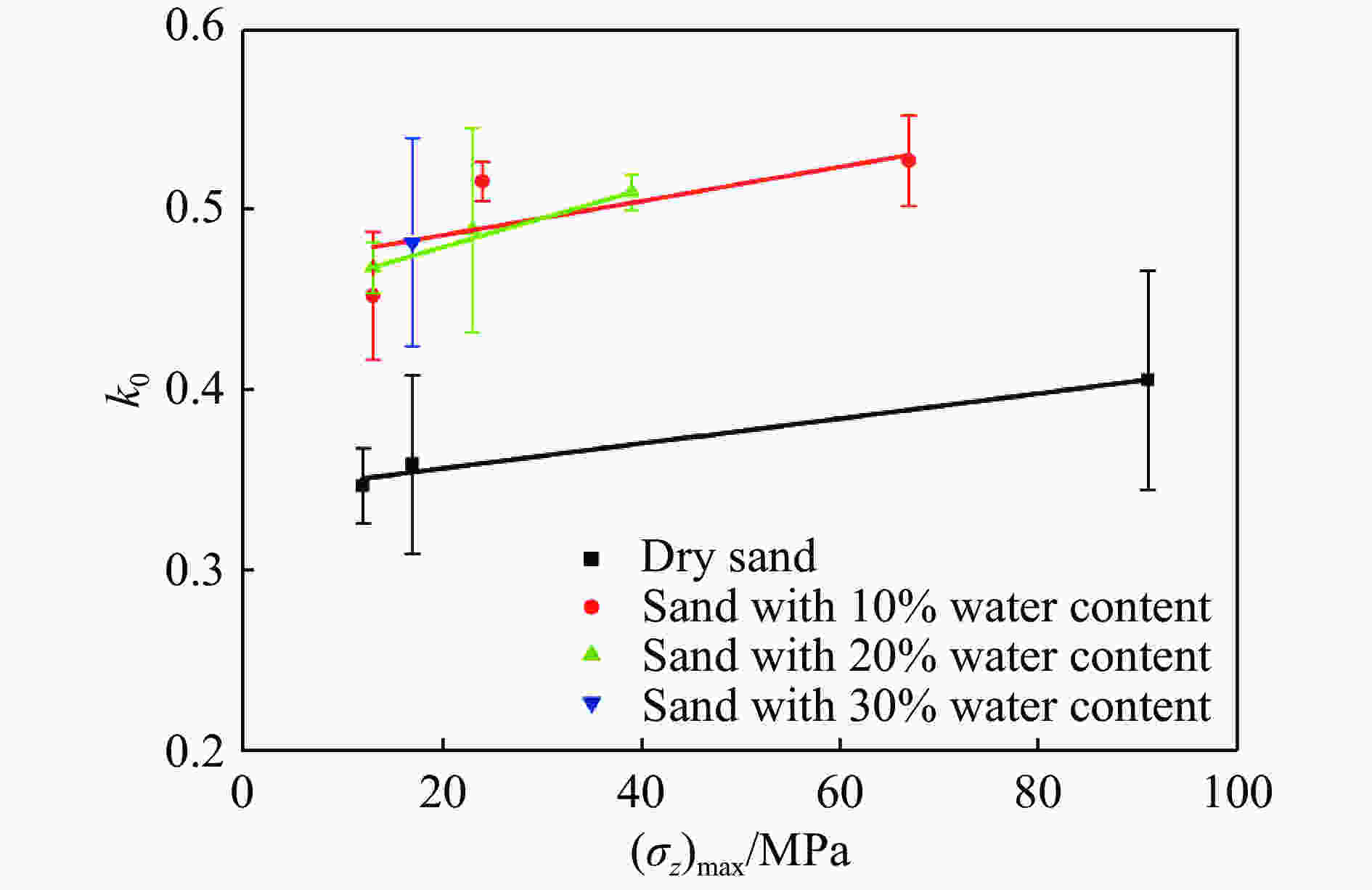
摘要: 使用经过系统标定的霍普金森压杆试验装置对不同含水率钙质砂进行了在准一维应变条件下的动态压缩试验，试样的平均应变率为209～1 137 s⁻¹。试验结果表明：半导体应变片灵敏系数和压杆弥散关系的标定对试验结果的准确性具有重要影响；当钙质砂应变小于0.025时潮湿试样的切向模量高于干燥试样，而在应变大于0.025时则相反；潮湿钙质砂的切线模量随含水率的增加先减后增。通过分析非饱和钙质砂在锁变后其轴向应力应变曲线及侧压力系数的变化规律，提出了非饱和钙质砂锁变现象的模型。
- 非饱和钙质砂 /
- 含水率 /
- 霍普金森压杆 /
- 半导体应变片 /
- 侧压力系数 /
- 锁变现象
Abstract: The dynamic compression tests of calcareous sands with different moisture contents under quasi-one-dimensional strain conditions were carried out using a calibrated SHPB system in the average strain rate ranging from 209 s⁻¹ to 1137 s⁻¹. The test results show that the calibration of the sensitivity coefficient of the semiconductor strain gauge and the dispersion of the pressure bar have a significant influence on the accuracy of the test results. When the strain of the calcareous sand is below 0.025, the tangential modulus of moist calcareous sand is higher than that of dry sand, but the opposite is true when the strain is above 0.025. The tangential modulus of moist samples decreases first and then increases with the increase of the water content. By analyzing the variation of axial stress-strain curve and lateral pressure coefficient of unsaturated calcareous sand after lock-in phenomenon, a model of the phenomenon of unsaturated calcareous sand is proposed.
- unsaturated calcareous sand /
- moist content /
- split Hopkinson pressure bar /
- semiconductor strain gauge /
- lateral pressure coefficient /
- lock-in phenomenon

HTML全文

图 1 钙质砂颗粒分配曲线

Figure 1. The particle distribution curve of calcareous sand

下载: 全尺寸图片幻灯片

图 2 SHPB试验系统示意图

Figure 2. The schematic diagram of SHPB system

下载: 全尺寸图片幻灯片

图 3 压杆弥散关系的标定

Figure 3. Calibration of dispersion of the bar

下载: 全尺寸图片幻灯片

图 4 半导体应变片标定结果

Figure 4. Calibration results of the semiconductor strain gauge

下载: 全尺寸图片幻灯片

图 5 装样容器

Figure 5. Specimen container

下载: 全尺寸图片幻灯片

图 6 压杆三维效应的修正对轴向应力(σ_z)测试结果

Figure 6. Effect of three dimensional effect correction of the bar on test results on axial stress (σ_z)

下载: 全尺寸图片幻灯片

图 7 不同含水率下钙质砂的轴向应力(σ_z)应变(ε_z)曲线

Figure 7. The axial stress (σ_z)-strain (ε_z) curves of calcareous sand with different water contents

下载: 全尺寸图片幻灯片

图 8 含水率对钙质砂轴向应力(σ_z)应变(ε_z)关系的影响

Figure 8. Effect of water content on axial stress (σ_z)-strain (ε_z) relation of calcareous sand

下载: 全尺寸图片幻灯片

图 9 30%含水率试样的侧压力系数时程曲线

Figure 9. Lateral pressure coefficient time profile of specimen with 30% water content

下载: 全尺寸图片幻灯片

图 10 侧压力系数(k₀)与轴向应力峰值((σ_z)_max)关系

Figure 10. The relationship between lateral pressure coefficient (k₀) and peak axial stress ((σ_z)_max)

下载: 全尺寸图片幻灯片

图 11 锁变现象中封闭孔隙的示意图

Figure 11. The schematic diagram of a closed pore in a locking-up phenomenon

下载: 全尺寸图片幻灯片

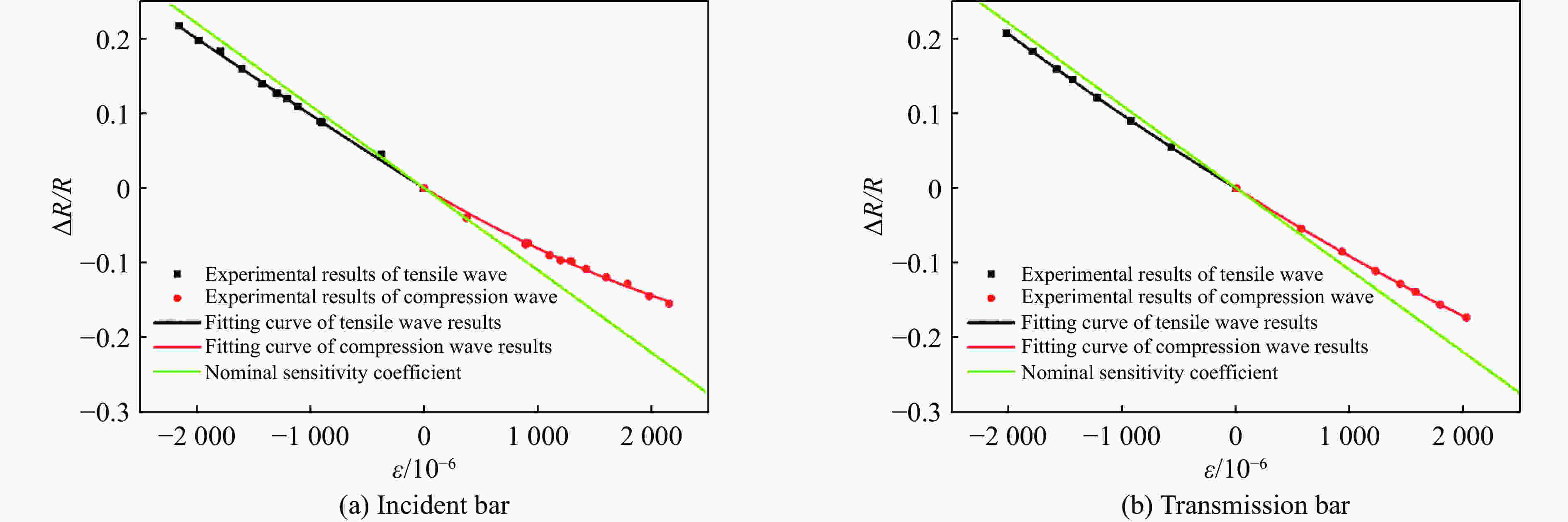
表 1 半导体应变片标定结果

Table 1. Calibration results of semiconductor strain gauges

信号类型	K₁	K₂	R²
入射杆压缩波	91.0	9 275	0.997
入射杆拉伸波	95.0	1 890	0.998
透射杆压缩波	93.6	4 500	0.998
透射杆拉伸波	97.1	1 537	0.999

下载: 导出CSV

表 2 SHPB试验工况表

Table 2. Test table of SHPB experiments

干密度/(g∙cm⁻³)	名义含水率/%	试验组编号	平均子弹速度/(m∙s⁻¹)	平均应变率/s⁻¹
1.40	1	CS001	21.43	1 128
		CS002	9.78	487
		CS003	4.02	335
1.40	10	CS101	18.52	1 118
		CS102	9.03	551
		CS103	3.62	242
1.40	20	CS201	18.04	1 137
		CS202	9.01	533
		CS203	3.61	209
1.40	30	CS301	18.14	836
		CS302	9.13	522
		CS303	3.56	243

下载: 导出CSV

表 3 非饱和砂土锁变现象试验结果的统计

Table 3. Experimental results of unsaturated sands with locking-up phenomenon

结果	$\dot \varepsilon $/s^-1	(σ_z)_max/MPa	砂土种类	C_u	e₀	S_r/%	M/GPa	R
Veyera^[12]	1 000	220	Eglin石英砂	3.41	0.51	60	3.32	0.56
		220	Eglin石英砂	3.41	0.51	80	2.85	0.44
		180	Tyndall石英砂	1.18	0.654	80	3.65	0.82
		211	Ottawa石英砂	1.5	0.545	80	3.24	0.86
Luo^[34]	600	300	Quikrete 砂	2.33	0.55	64	—	0.68
Luo^[34]	600	300	Quikrete 砂	2.33	0.55	85	—	0.59
Barr^[13]	3 500	240	松散石英砂	2.2	0.77	25	3.17	1.02
Barr^[13]	3 500	240	松散石英砂	2.2	0.77	52	3.35	1.01
本文	500	70	密实钙质砂	>6	1.01	57	—	1.02
本文	500	70	密实钙质砂	>6	1.01	86	2.34	1.11
注：$\dot \varepsilon $为应变率；C_u为不均匀系数；e₀为初始孔隙比；S_r为试样饱和度；M为锁变模量。

下载: 导出CSV

参考文献(36)

刘崇权, 杨志强, 汪稔. 钙质土力学性质研究现状与进展 [J]. 岩土力学, 1995(4): 74–84.

LIU C Q, YANG Z Q, WANG R. The present condition and development in studies of mechanical properties of calcareous soils [J]. Rock and Soil Mechanics, 1995(4): 74–84.

DATTA M, RAO G V, GULHATI S K. The nature and engineering behavior of carbonate soils at Bombay High, India [J]. Marine Geotechnology, 1981, 4(4): 307–341. DOI: 10.1080/10641198109379830.

STERIANOS B. Geotechnical properties of carbonate soils with reference to an improved engineering classification [D]. Rondebosch: University of Cape Town, 1988: 1−4.

ALBA J L, AUDIBERT J M. Pile design in calcareous and carbonaceous granular materials, and historic review [C] // Proceedings of the 2nd international conference on engineering for calcareous sediments. Rotterdam: AA Balkema. 1999, 1: 29−44.

WANG X, JIAO Y, WANG R, et al. Engineering characteristics of the calcareous sand in Nansha Islands, South China Sea [J]. Engineering Geology, 2011, 120(1): 40–47. DOI: 10.1016/j.enggeo.2011.03.011.

曹梦, 叶剑红. 南海钙质砂蠕变-应力-时间四参数数学模型 [J]. 岩土力学, 2019(5): 1771–1777. DOI: 10.16285/j.rsm.2018.1267.

CAO M, YE J H. Creep-stress-time four parameters mathematical model of calcareous sand in South China Sea [J]. Rock and Soil Mechanic, 2019(5): 1771–1777. DOI: 10.16285/j.rsm.2018.1267.

AL-DOURI R H, POULOS H G. Static and cyclic direct shear tests on carbonate sands [J]. Geotechnical Testing Journal, 1992, 15(2): 138–157. DOI: 10.1520/GTJ10236J.

COOP M R. The mechanics of uncemented carbonate sands [J]. Géotechnique, 1990, 40(4): 607–626. DOI: 10.1680/geot.1990.40.4.607.

COOP M R, ATKINSON J H. The mechanics of cemented carbonate sands [J]. Géotechnique, 1993, 43(1): 53–67. DOI: 10.1680/geot.1993.43.1.53.

文祝, 邱艳宇, 紫民, 等. 钙质砂的准一维应变压缩试验研究 [J]. 爆炸与冲击, 2019, 39(3): 1–11. DOI: 10.11883/bzycj-2018-0015.

WEN Z, QIU Y Y, ZI M, et al. Experimental study on quasi-one-dimensional strain compression of calcareous sand [J]. Explosion and Shock Waves, 2019, 39(3): 1–11. DOI: 10.11883/bzycj-2018-0015.

魏久淇, 王明洋, 邱艳宇, 等. 钙质砂动态力学特性试验研究 [J]. 振动与冲击, 2018, 37(24): 7–12. DOI: 10.13465/j.cnki.jvs.2018.24.002.

WEI J Q, WANG M Y, QIU Y Y, et al. Impact compressive response of calcareous sand [J]. Journal of Vibration and Shock, 2018, 37(24): 7–12. DOI: 10.13465/j.cnki.jvs.2018.24.002.

VEYERA G E. Uniaxial stress-strain behavior of unsaturated soils at high strain rates: WR-TL-93-3523 [R]. Fort Belvoir, VA: Defense Technical Information Center, 1994.

BARR A D, CLARKE S D, TYAS A, et al. Effect of moisture content on high strain rate compressibility and particle breakage in loose sand [J]. Experimental Mechanics, 2018, 58(8): 1331–1334. DOI: 10.1007/s11340-018-0405-4.

王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2010: 52−60.

胡时胜, 唐志平, 王礼立. 应变片技术在动态力学测量中的应用 [J]. 实验力学, 1987(2): 75–84.

HU S S, TANG Z P, WANG L L. Application of strain gage technique in dynamic measurement [J]. Journal of Experimental Mechanics, 1987(2): 75–84.

BUSSAC M N, COLLET P, GARY G, et al. An optimization method for separating and rebuilding one-dimensional dispersive waves from multi-point measurements: application to elastic or viscoelastic bars [J]. Journal of the Mechanics and Physics of Solids, 2002, 50(2): 321–349. DOI: 10.1016/S0022-5096(01)00057-6.

TYAS A, WATSON A J. An investigation of frequency domain dispersion correction of pressure bar signals [J]. International Journal of Impact Engineering, 2001, 25(1): 87–101. DOI: 10.1016/S0734-743X(00)00025-7.

TYAS A, POPE D J. Full correction of first-mode Pochammer-Chree dispersion effects in experimental pressure bar signals [J]. Measurement Science and Technology, 2005, 16(3): 642. DOI: 10.1088/0957-0233/16/3/004.

BACON C. An experimental method for considering dispersion and attenuation in a viscoelastic Hopkinson bar [J]. Experimental Mechanics, 1998, 38(4): 242–249. DOI: 10.1007/BF02410385.

LOVE A E H. A Treatise on the mathematical theory of elasticity [M]. 4th ed. New York: Dover Publications, 1944: 289−291.

SONG B, CHEN W, LUK V. Impact compressive response of dry sand [J]. Mechanics of Materials, 2009, 41(6): 777–785. DOI: 10.1016/j.mechmat.2009.01.003.

MARTIN B E, KABIR M E, CHEN W. Undrained high-pressure and high strain-rate response of dry sand under triaxial loading [J]. International Journal of Impact Engineering, 2013, 54: 51–63. DOI: 10.1016/j.ijimpeng.2012.10.008.

SEMBLAT J, LUONG M P, GARY G. 3D-Hopkinson bar: new experiments for dynamic testing on soils [J]. Soils and Foundations, 1999, 39(1): 1–10. DOI: 10.3208/sandf.39.1.

KABIR E. Dynamic behavior of granular materials [D]. Indiana: Purdue University, 2010: 13−35.

FARR J V. Loading rate effects on the one-dimensional compressibility of four partially saturated soils [R]. Army Engineer Waterways Experiment Station Vicksburg MS Structures LAB, 1986: 373.

谢定义. 非饱和土土力学[M]. 北京: 高等教育出版社, 2015: 10.

MULILIS J P, ARULANANDAN K, MITCHELL J K, et al. Effects of sample preparation on sand liquefaction [J]. Journal of the Geotechnical Engineering Division, 1977, 103(2): 91–108.

LADD R S. Specimen preparation and cyclic stability of sands [J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 1977, 103: 535–547.

JUANG C H, HOLTZ R D. Fabric, pore size distribution, and permeability of sandy soils [J]. Journal of Geotechnical Engineering, 1986, 112(9): 855–868. DOI: 10.1061/(ASCE)0733-9410(1986)112:9(855).

NIMMO J R, AKSTIN K C. Hydraulic conductivity of a sandy soil at low water content after compaction by various methods [J]. Soil Science Society of America Journal, 1988, 52(2): 303–310. DOI: 10.2136/sssaj1988.03615995005200020001x.

PIERCE J, CHARLIE W A. High-intensity compressive stress wave propagation through unsaturated sands: ESL-TR-90-12 [R]. Tyndall: Air Force Engineering and Services Center, 1990.

MARTIN B E, CHEN W, SONG B, et al. Moisture effects on the high strain-rate behavior of sand [J]. Mechanics of Materials, 2009, 41(6): 786–798. DOI: 10.1016/j.mechmat.2009.01.014.

FELICE C W. The response of soil to impulse loads using the split-Hopkinson pressure bar technique [D]. Utah: The University of Utah, 1986: 246−291.

LUO H Y, COOPER W L, LU H B. Effects of particle size and moisture on the compressive behavior of dense Eglin sand under confinement at high strain rates [J]. International Journal of Impact Engineering, 2014, 65: 40–55. DOI: 10.1016/j.ijimpeng.2013.11.001.

BLOUIN S E, KWANG J K. Undrained compressibility of saturated soil: DNA-TR-87-42 [R]. USA: ARA, 1984.

AKERS S A. Two-dimensional finite element analysis of porous geomaterials at multikilobar stress levels [D]. Virginia: Virginia Tech., 2001: 124.

施引文献

资源附件(0)

访问统计