Study on similarity law of non-proportionally scaled penetration/perforation test
-
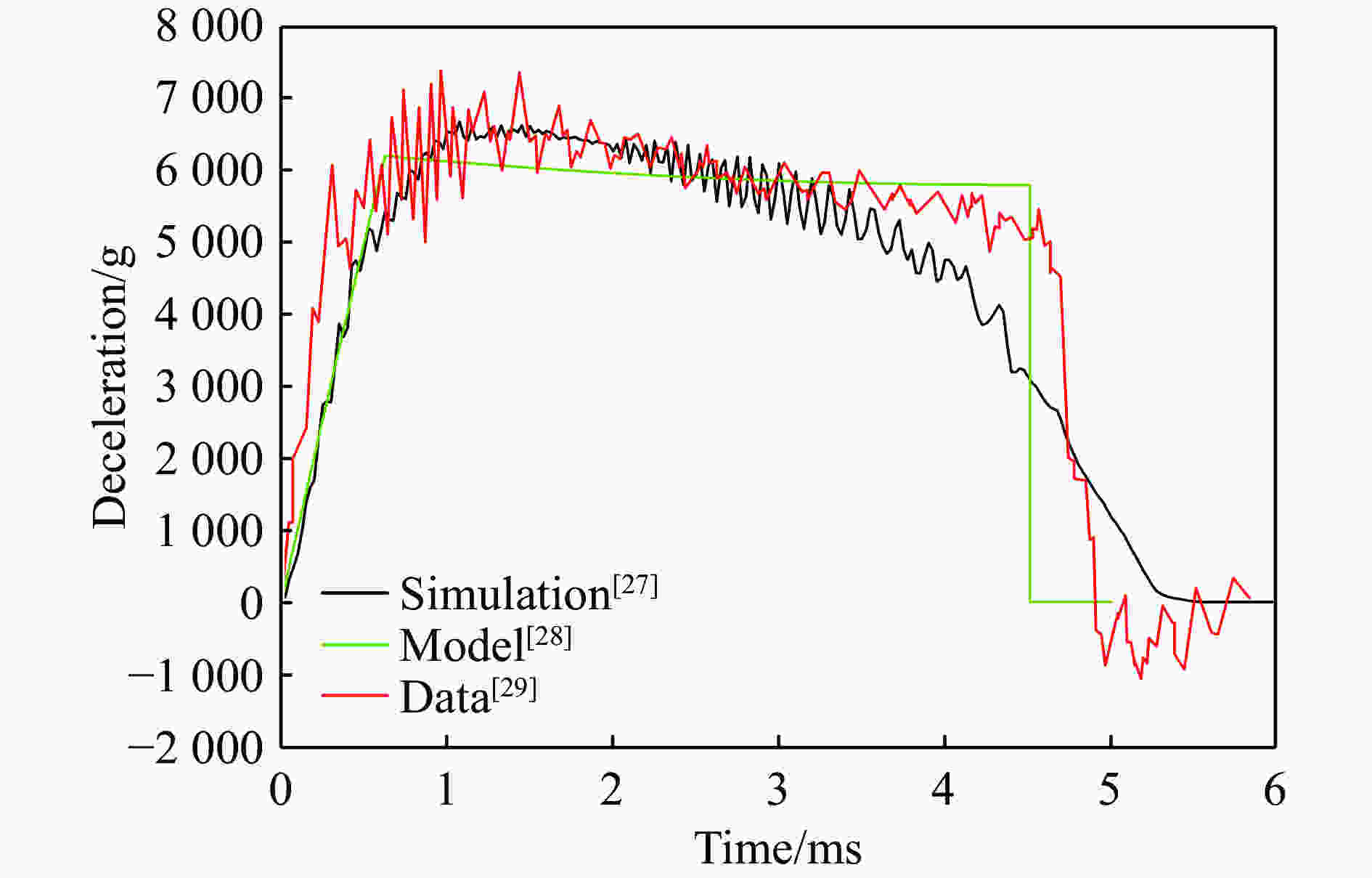
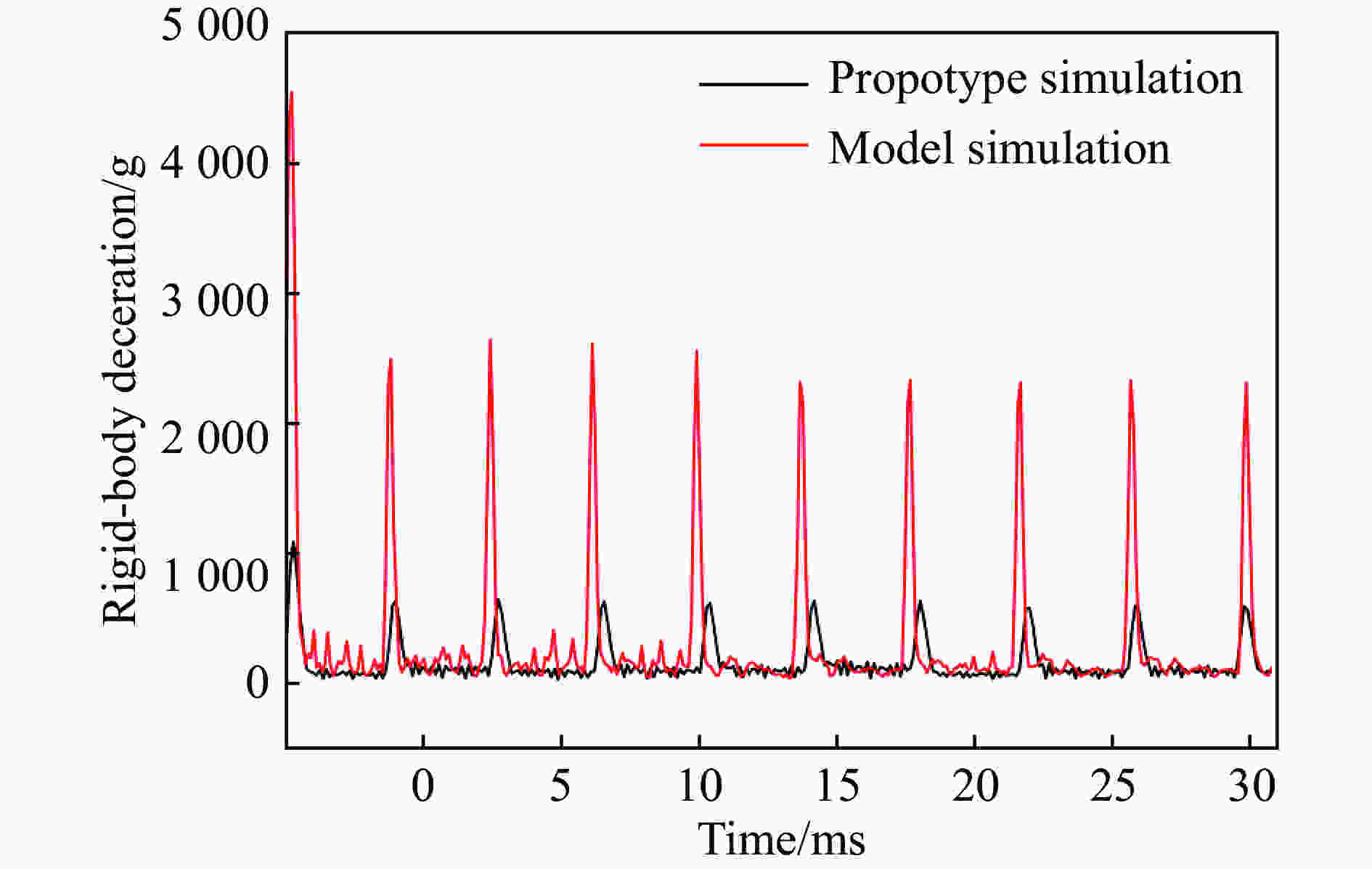
摘要: 高速侵彻弹体的弹载部件/关键元器件的生存性与可靠性考核是引战系统研制领域的热点与难点问题,受原型试验的成本限制,利用缩比弹体搭载原型引信部件开展非等比例缩比试验研究是可行途径。针对传统等比例缩比方案无法满足弹体刚体过载相似性要求的情况,研究了非等比例缩比侵彻/贯穿相似规律,提出了非等比例缩比侵彻试验设计方法。数值计算结果表明:侵彻半无限厚混凝土靶条件下,非等比例缩比弹刚体过载的脉宽、幅值均可实现与原型弹刚体过载一致的加载条件;贯穿多层薄靶的条件下,通过调节靶板布置及弹体初速等试验工况,合理设计缩比弹体结构,可使非等比例缩比试验的弹体刚体过载峰值和脉宽覆盖原型试验。通过缩比模型试验得到的刚体过载特性可以为弹体及引信部件抗过载防护设计提供可靠的参考依据。Abstract: Survivability and reliability assessment of components/key components on high-speed penetrating projectiles is a hot and difficult issue in the field of EPW development. Due to the cost limitation of prototype test, it is feasible to carry out non-proportionally scale experimental research by carrying prototype fuze components on scaled projectiles. Through the analysis of the process mechanism of a projectile penetrating concrete target, the analytic solution of rigid-body deceleration when the projectile penetrating the semi-infinite thick concrete target and the multi-layer thin concrete target are discussed respectively. From the point of view of similarity of rigid-body deceleration, the non-proportionally reduced-scale criterion of projectile is proposed when the traditional scaling scheme can not meet the requirements of similarity. The numerical results show that under the condition of penetrating semi-infinite thick concrete target, the rigid-body deceleration of the non-proportionally reduced-scale projectile can achieve the same conditions as which of the prototype projectile from the point of view of pulse width and amplitude; under the condition of penetrating multi-layered thin target, through reasonably setting the scale factor and adjusting the layout of the target plate and the initial velocity of the projectile. The pulse width and amplitude of the rigid-body deceleration in the reduced scale test can cover them in the prototype test. The rigid body deceleration characteristics obtained from scaled model test can provide reliable overload environment reference for missile projectile design.
-
表 1 模型和原型物理量缩比因子
Table 1. Scaling factors of physical quantities between model and prototype
变量 量纲 原型与模型参量比 缩比因子 特征尺寸 L lp/lm n 时间 T tp/tm n 质量 M Mp/Mm n3 密度 ML−3 ρp/ρm 1 应力 ML−1T−2 σp/σm 1 过载 LT−2 ap/am 1/n 速度 LT−1 Vp/Vm 1 表 2 原型弹的弹靶参数
Table 2. Expemrimental parameters of prototype projectiles and targets
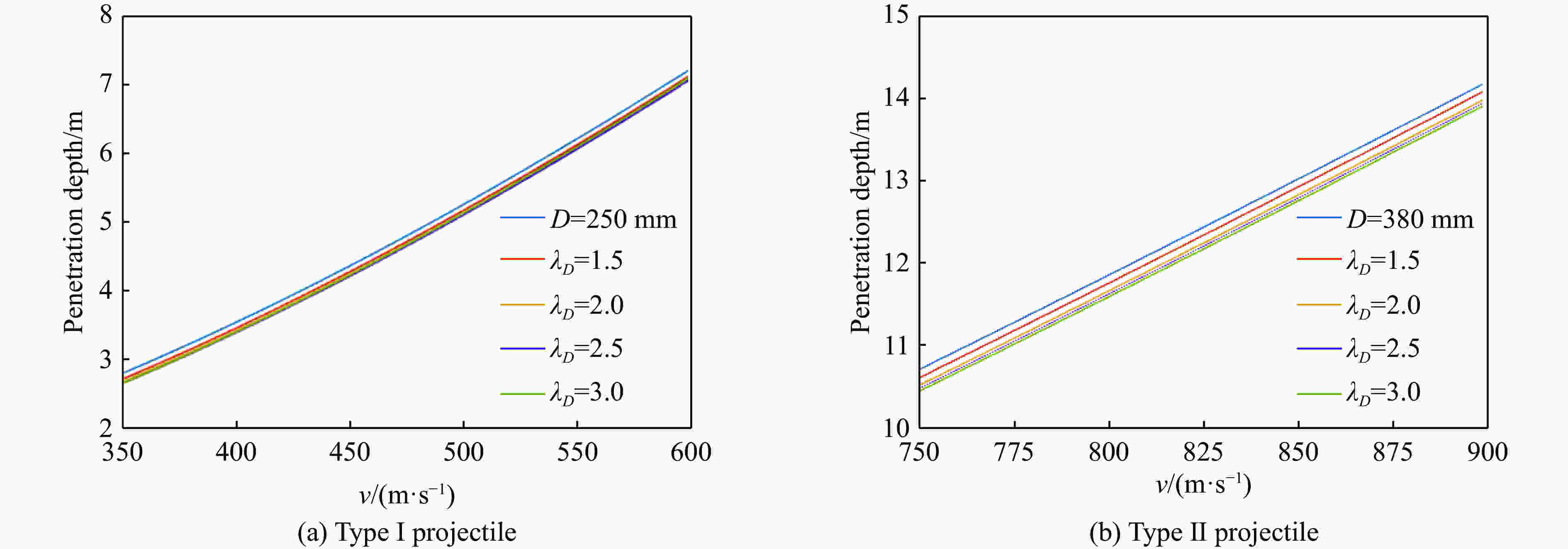
弹型 D/mm M/kg l/mm ηCRH v0/(m∙s−1) ρt/(kg∙m-3) fc/MPa Ⅰ 250 500 2 000 3.5 450 2 420 45 Ⅱ 380 1 200 2 500 3.5 850 2 420 45 表 3 缩比系数表
Table 3. Scaling parameters of prototype projectiles
缩比弹序号 λD λM λb λe 1 1.50 2.25 1.20 1.20 2 2.00 4.00 1.30 1.20 3 2.50 6.25 1.50 1.20 4 3.00 9.00 1.60 1.20 表 4 Ⅱ型(1 000 kg级)弹原型试验及对应的缩比试验参数
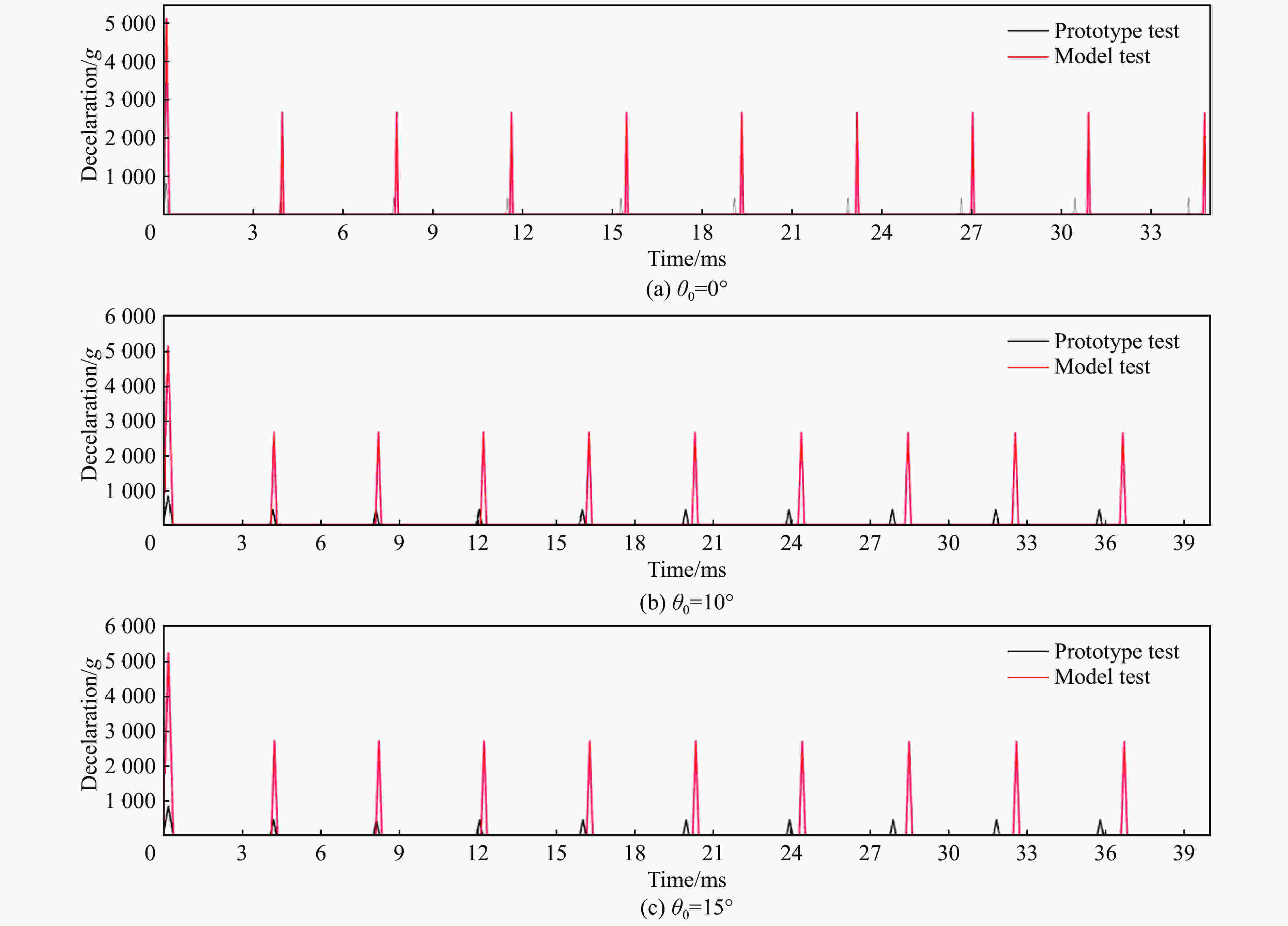
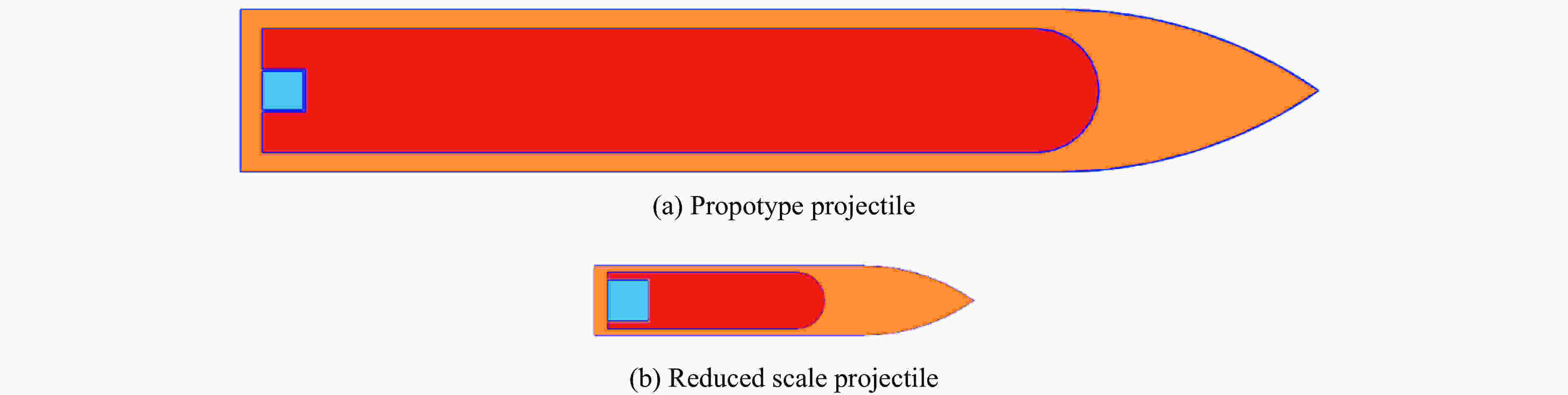
Table 4. Prototype test and corresponding scaling test parameters of type II (1 000 kg) projectile
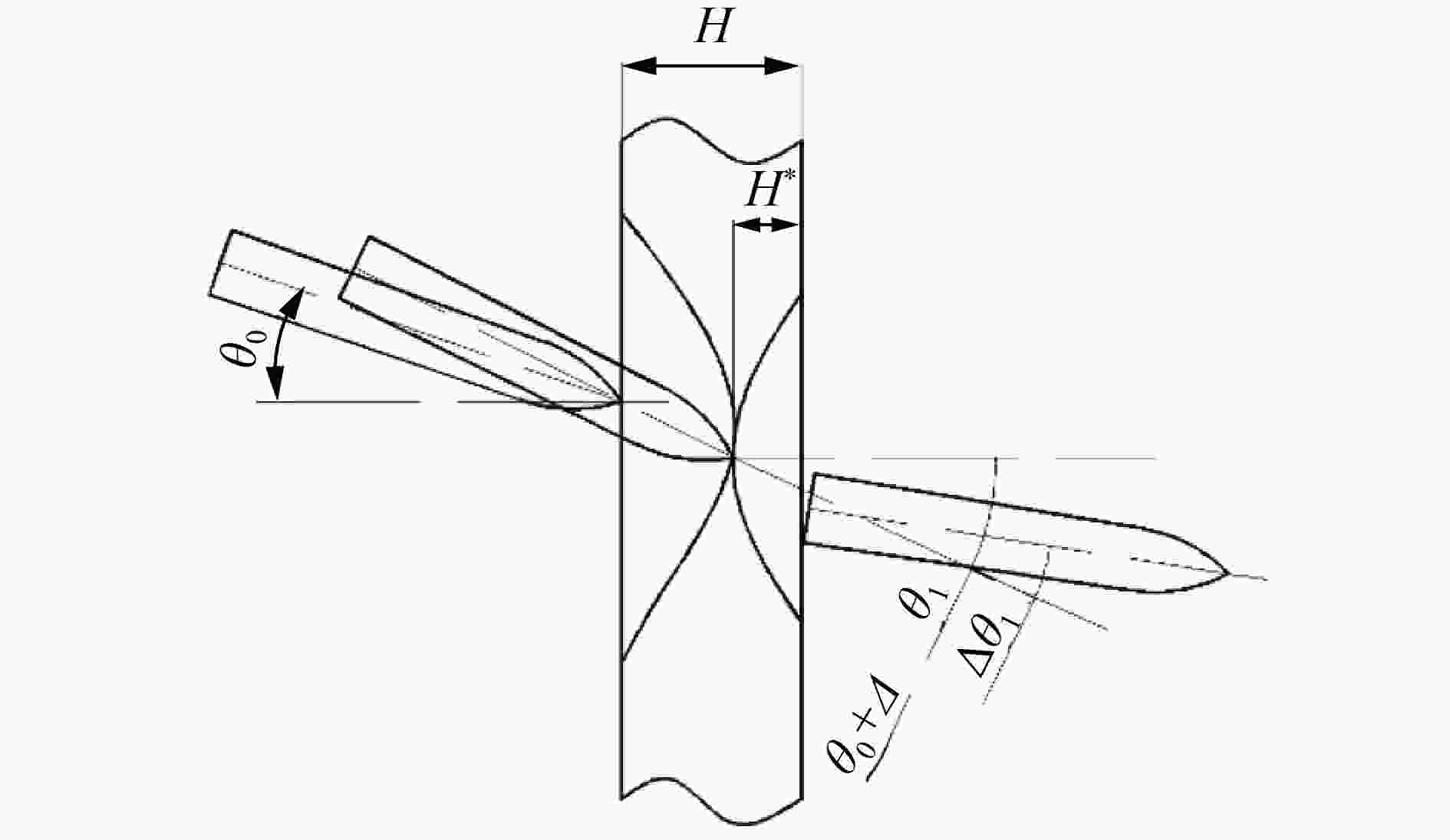
量 原型试验 缩比试验 相关缩比系数 M/kg 1 200 80 λM=15 l/mm 2 500 890 λl=2.8 D/mm 380 150 ${\lambda _D}{\rm{ = }}2.5$ ηCRH 3 3 v0/(m∙s−1) 850 850 ${\lambda _{{v_0}}} = 1$ θ0/(°) 0/10/15 0/10/15 H/mm 300+180×9 300+140×9 λH=1和1.35 z/mm 3 000 2 900 ${\lambda _z}{\rm{ = }}0.97$ σbc/MPa 40 30 λfc=0.75 注:z为靶间距;σbc为靶材料抗压强度。 表 5 1 000 kg级原型弹及其缩比弹自由状态下前20阶模态频率
Table 5. Top 20 modal frequencies of 1 000 kg class prototype projectile and reduced scale projectile in free state
模态序号 模态频率/Hz 模态序号 模态频率/Hz 原型弹 缩比弹 原型弹 缩比弹 7 335.67 1 159.2 14 1 416.2 4 670.5 8 335.67 1 159.2 15 1 453.2 4 670.5 9 716.72 2 132.5 16 2 012.8 6 291.2 10 833.99 2 708.3 17 2 012.8 6 291.2 11 833.99 2 708.3 18 2 200.1 6 463.9 12 1 085.9 3 196.4 19 2 236.0 7 044.5 13 1 416.2 4 563.3 20 2 633.9 8 244.7 -
[1] 王树有, 顾晓辉, 赵有守. 混凝土侵彻试验相似准则验证分析 [J]. 南京理工大学学报(自然科学版), 2005, 29(5): 43–46. DOI: 10.3969/j.issn.1005-9830.2005.05.011.WANG S Y, GU X H, ZHAO Y H. Experimental analysis of simularity criteria for concrete penetration [J]. Journal of Nanjing University of Science and Technology (Natural Science), 2005, 29(5): 43–46. DOI: 10.3969/j.issn.1005-9830.2005.05.011. [2] 王世虎. 硬目标侵彻中的加速度信号研究[D]. 北京: 北京理工大学, 2010: 5−30. [3] FORRESTAL M J, FREW D J, HICKERSON J P, et al. Penetration of concrete targets with deceleration-time measurements [J]. International Journal of Impact Engineering, 2003, 28(5): 479–497. DOI: 10.1016/S0734-743X(02)00108-2. [4] FREW D J, FORRESTAL M J, Cargile J D. The effect of concrete target diameter on proticle deceleration and penetration depth [J]. International Journal of Impact Engineering, 2006, 32(10): 1584–1594. DOI: 10.1016/j.ijimpeng.2005.01.012. [5] XU Y, KEER L M, LUK V K. Elastic-cracked model for penetration into un-reinforced concrete targets with ogival nose projectiles [J]. International Journal Solids Structures, 1997, 34(12): 1479–1491. DOI: 10.1016/S0020-7683(96)00099-6. [6] LUNDGREN. A strain gage based projectile health monitor and salvage indicating circuit for kinetic energy penetrating projectiles [C] // 53th NDIA Fuze Conferenc. Florida: NDIA, 2009. [7] 刘小虎, 刘吉, 王乘, 等. 弹丸低速垂直侵彻无钢筋混凝土的实验研究 [J]. 爆炸与冲击, 1999, 19(4): 323–328.LIU X H, LIU J, WANG C, et al. Experimental studies on the projectile penetrating normally into a plain concrete [J]. Explosion and Shock Waves, 1999, 19(4): 323–328. [8] 杨明, 杨志刚, 林祖森. 加速度计输出信号的信息组成 [J]. 中北大学学报(自然科学版), 2000, 21(1): 44–46. DOI: 10.3969/j.issn.1673-3193.2000.01.012.YANG M, YANG Z G, LIN Z S. Information compositions of the output signal of accelerometers [J]. Journal of North China Institute of Technology (Natural Science Edtition), 2000, 21(1): 44–46. DOI: 10.3969/j.issn.1673-3193.2000.01.012. [9] ZHANG W, CHEN L, XIONG J, et al. Ultra-high g deceleration-time measurement for the penetration into steel target [J]. International Journal of Impact Engineering, 2007, 34(3): 436–447. DOI: 10.1016/j.ijimpeng.2006.01.008. [10] 徐鹏, 祖静, 范锦彪. 高速动能弹侵彻硬目标加速度测试技术研究 [J]. 振动与冲击, 2007, 26(11): 118–122. DOI: 10.3969/j.issn.1000-3835.2007.11.028.XU P, ZU J, FAN J B. Study on acceleration test technique of high velocity kinetic energy projectile penetrating into hard target [J]. Journal of Vibration and Shock, 2007, 26(11): 118–122. DOI: 10.3969/j.issn.1000-3835.2007.11.028. [11] 何丽灵, 高进忠, 陈小伟, 等. 弹体高过载硬回收测量技术的实验探讨 [J]. 爆炸与冲击, 2013, 33(6): 608–612. DOI: 10.11883/1001-1455(2013)06-0608-0612.HE L L, GAO J Z, CHEN X W, et al. Experimental study on measurement technology for projectile deceleration [J]. Explosion and Shock Waves, 2013, 33(6): 608–612. DOI: 10.11883/1001-1455(2013)06-0608-0612. [12] 周宁, 任辉启, 沈兆武, 等. 侵彻钢筋混凝土过程中弹丸过载特性的实验研究 [J]. 实验力学, 2006, 21(5): 572–578. DOI: 10.3969/j.issn.1001-4888.2006.05.005.ZHOU N, REN Q H, SHEN Z W, et al. Experimental study on overload characteristics of projectile penetrating reinforced concrete [J]. Journal of Experimental Mechanics, 2006, 21(5): 572–578. DOI: 10.3969/j.issn.1001-4888.2006.05.005. [13] 黄家蓉, 刘瑞朝, 何翔, 等. 侵彻过载测试信号的数据处理方法 [J]. 爆炸与冲击, 2009, 29(5): 555–560. DOI: 10.11883/1001-1455(2009)05-0555-0560.HUANG J R, LIU R C, HE X, et al. A new data processing technique for measured penetration overloads [J]. Explosion and Shock Waves, 2009, 29(5): 555–560. DOI: 10.11883/1001-1455(2009)05-0555-0560. [14] 赵生伟, 初哲, 李明. 抗侵彻过载战斗部装药安定性实验研究 [J]. 兵工学报, 2010, 31(S1): 284–287.ZHAO S W, CHU Z, LI M. Experiment investigation on stability of explosive in anti-overload warhead [J]. Acta Armamentarii, 2010, 31(S1): 284–287. [15] 张会锁, 罗旭, 张远高. 弹体过载记录仪安装方式对侵彻过载峰值的影响分析 [J]. 中北大学学报(自然科学版), 2014, 35(3): 252–257. DOI: 10.3969/j.issn.1673-3193.2014.03.006.ZHANG H S, LUO X, ZHANG Y G. Research on the influence of the missile overload recorder installation style on penetration acceleration peak value [J]. Journal of North University of China (Natural Science Edition), 2014, 35(3): 252–257. DOI: 10.3969/j.issn.1673-3193.2014.03.006. [16] 李计林, 徐文峥, 王晶禹, 等. 侵彻过程中弹载火工品过载特性数值模拟 [J]. 火工品, 2009(6): 30–34. DOI: 10.3969/j.issn.1003-1480.2009.06.010.LI J L, XU W J, WANG J Y, et al. The numerical simulation for overload characteristic of initiating explosive device on missile during penetration [J]. Initiators and Pyrotechnics, 2009(6): 30–34. DOI: 10.3969/j.issn.1003-1480.2009.06.010. [17] HALDAR A, HAMIEH H A. Local effect of solid missiles on concrete structures [J]. Journal of Structural Engineering, 1984, 110(5): 948–960. DOI: 10.1061/(ASCE)0733-9445(1984)110:5(948). [18] 徐建波. 长杆射弹对混凝土的侵彻特性研究[D]. 湖南: 国防科学技术大学, 2001: 23−56. [19] 杨超, 赵宝荣, 付克勤, 等. 缩比件弹体侵彻混凝土过程相似律研究 [J]. 兵器材料科学与工程, 2003(5): 3–7. DOI: 10.3969/j.issn.1004-244X.2003.05.001.YANG C, ZHAO B R, FU K Q, et al. Research on similarity law of penetration concrete of equiscale projectile [J]. Ordnance Material Science and Engineering, 2003(5): 3–7. DOI: 10.3969/j.issn.1004-244X.2003.05.001. [20] 武海军, 黄风雷, 陈利, 等. 动能弹侵彻钢筋混凝土相似性分析 [J]. 兵工学报, 2007, 28(3): 276–280. DOI: 10.3321/j.issn:1000-1093.2007.03.005.WU H J, HUANG F L, CHEN L, et al. Similarity law analyses of penetration behavior in reinforced concrete [J]. Acta Armamentarii, 2007, 28(3): 276–280. DOI: 10.3321/j.issn:1000-1093.2007.03.005. [21] 陈小伟, 张方举, 杨世全, 等. 动能深侵彻弹的力学设计(III): 缩比实验分析 [J]. 爆炸与冲击, 2006, 26(2): 105–114. DOI: 10.11883/1001-1455(2006)02-0105-0114.CHEN X W, ZHANG F J, YANG S Q, et al. Mechanics of structural design of epw (Ⅲ): investigations on the reduced-scale tests [J]. Explosion And Shock Waves, 2006, 26(2): 105–114. DOI: 10.11883/1001-1455(2006)02-0105-0114. [22] MEBAR Y. A method for scaling ballistic penetration phenomena [J]. International Journal of Impact Engineering, 1997, 19(9): 821–829. DOI: 10.1016/S0734-743X(97)00020-1. [23] YOUNG C W. Equations for predicting earth penetration by projectiles: an update: SAND88-0013 [R]. USA: Sandia National Laboratories, 1988. [24] LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile [J]. International Journal of Impact Engineering, 2003, 28(1): 93–116. DOI: 10.1016/S0734-743X(02)00037-4. [25] 朱彤. 结构动力模型相似问题及结构动力试验技术研究[D]. 大连: 大连理工大学, 2004. [26] MAI Y W, ATKINS A G. Crack propagation in non-proportionally scaled elastic structures [J]. International Journal of Mechanical Sciences, 1978, 20(7): 437–449. DOI: 10.1016/0020-7403(78)90033-4. [27] FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets [J]. International. Journal. Solids Structure, 1997, 34(31-32): 4127–4146. DOI: 10.1016/S0020-7683(97)00017-6. [28] MA Z F, DUAN Z P, OU Z C, et al. The experimental and theoretical research on attitude of projectile obliquely penetrating into thin concrete target [J]. Acta Armamentarii, 2015, 36(S1): 248–252. DOI: 10.15918/j.tbit1001-0645.2016.10.003. [29] 王冰. 大长径比弹体侵彻混凝土的数值模拟研究[D]. 北京: 北京理工大学, 2012: 5−30. [30] PENG Y, WU H, FANG Q, et al. Residual velocities of projectiles after normally perforating the thin ultra-high performance steel fiber reinforced concrete slabs [J]. International Journal of Impact Engineering, 2016, 97(11): 1–9. DOI: 10.1016/j.ijimpeng.2016.06.006. -







 下载:
下载: