磁驱动单侧飞片实验的数值模拟

阚明先; 王刚华; 肖波; 段书超; 张朝辉

doi:10.11883/bzycj-2019-0103

磁驱动单侧飞片实验的数值模拟

doi: 10.11883/bzycj-2019-0103

中国工程物理研究院流体物理研究所，四川绵阳 621999

基金项目: 国家自然科学基金（11571293）

详细信息

作者简介:
阚明先（1971－　），男，硕士，副研究员，kanmx@caep.cn

中图分类号: O361.3
计量
- 文章访问数: 5440
- HTML全文浏览量: 1293
- PDF下载量: 68
- 被引次数: 0
出版历程
- 收稿日期: 2019-04-01
- 修回日期: 2019-11-18
- 网络出版日期: 2020-02-25
- 刊出日期: 2020-03-01

Simulation on magnetically-driven one-sided flyer plate experiments

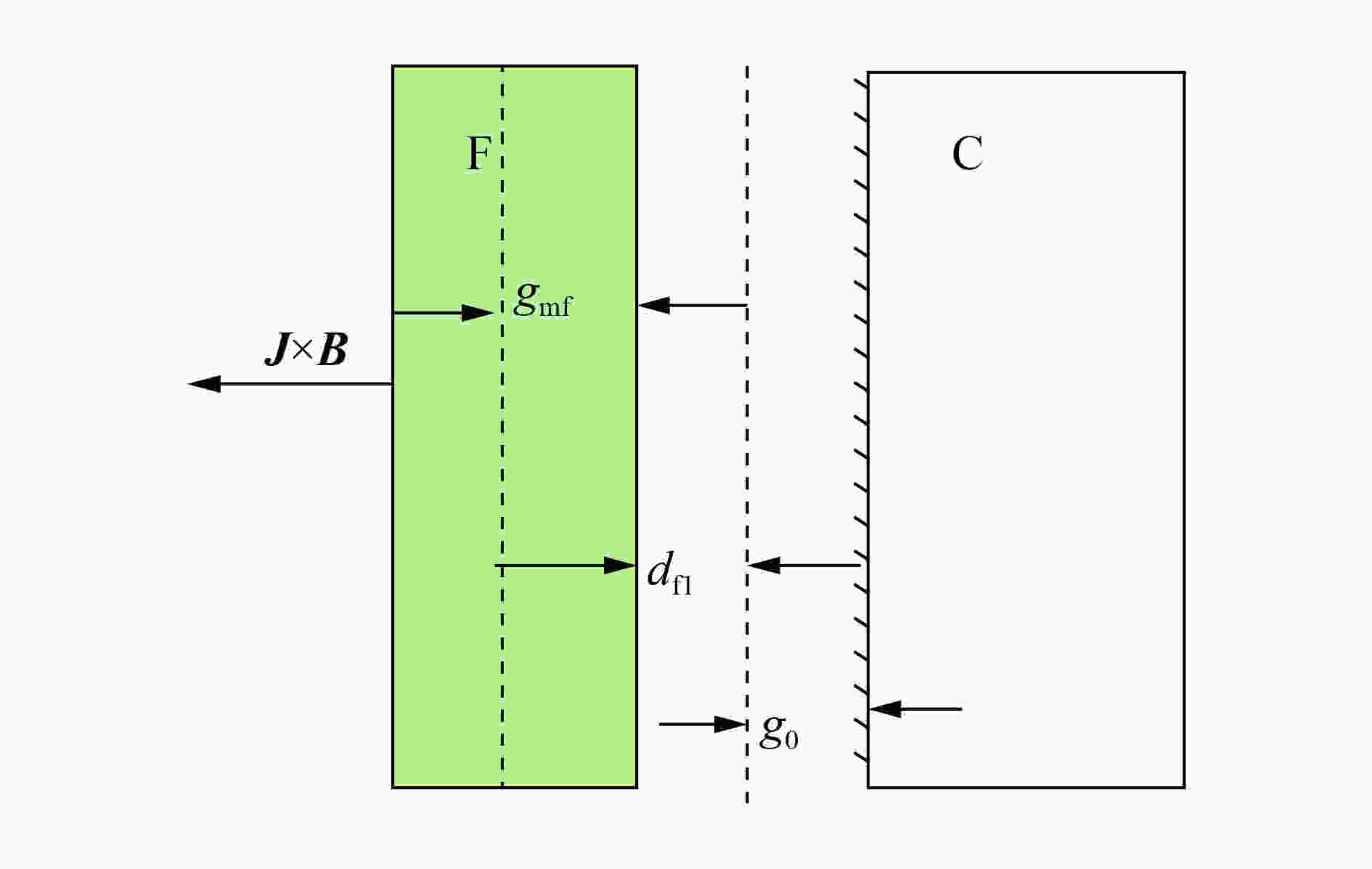
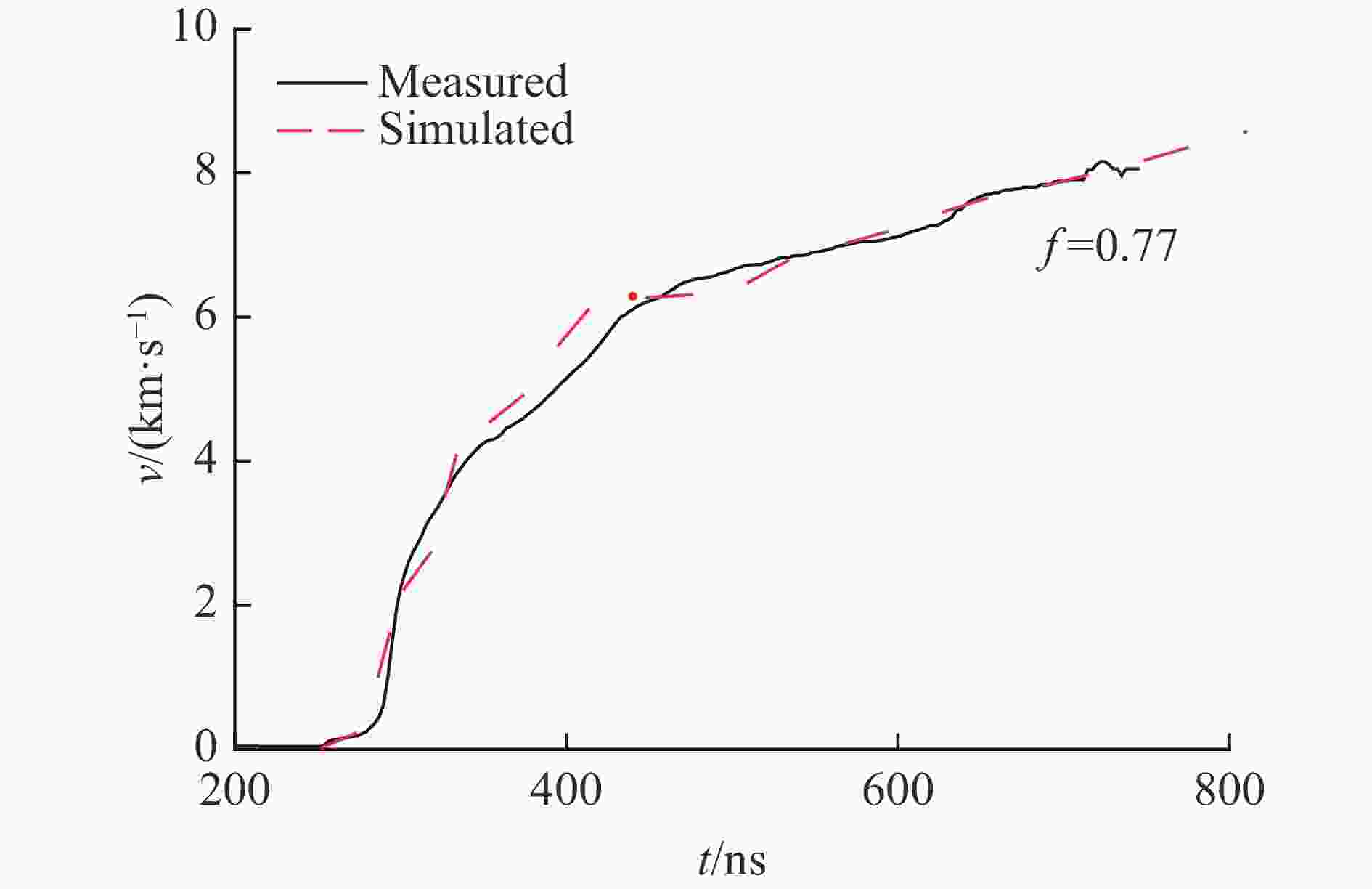
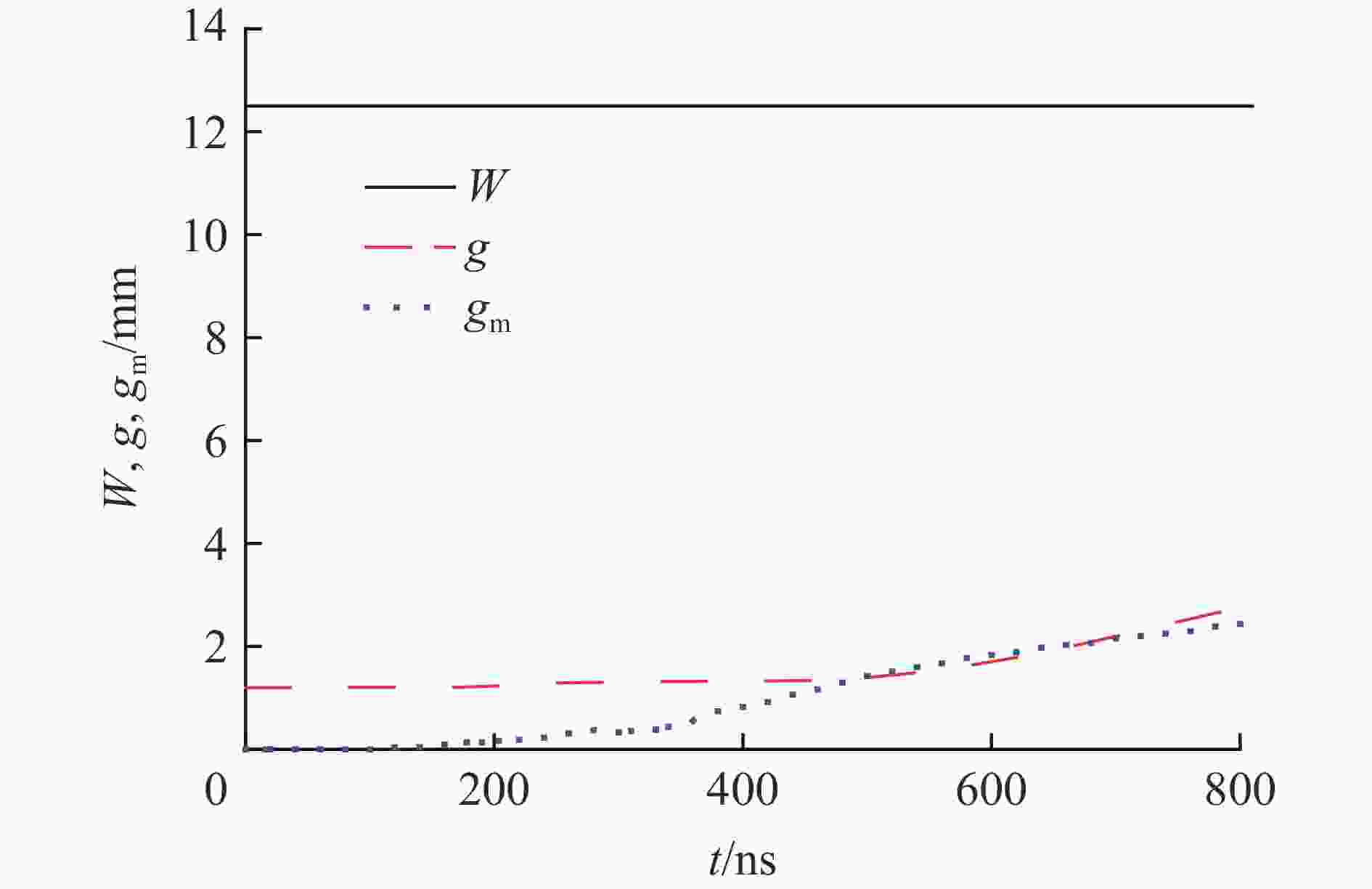
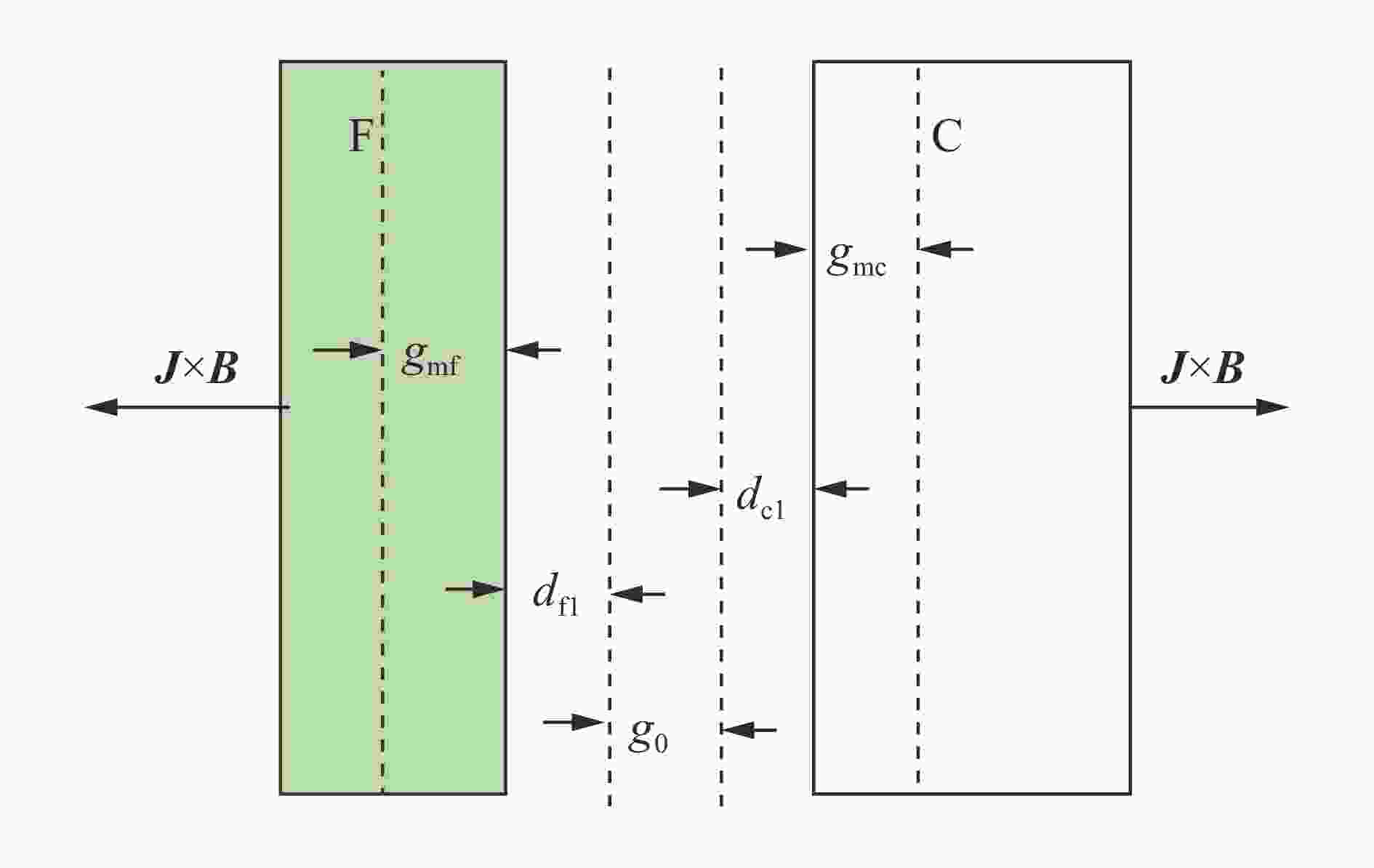
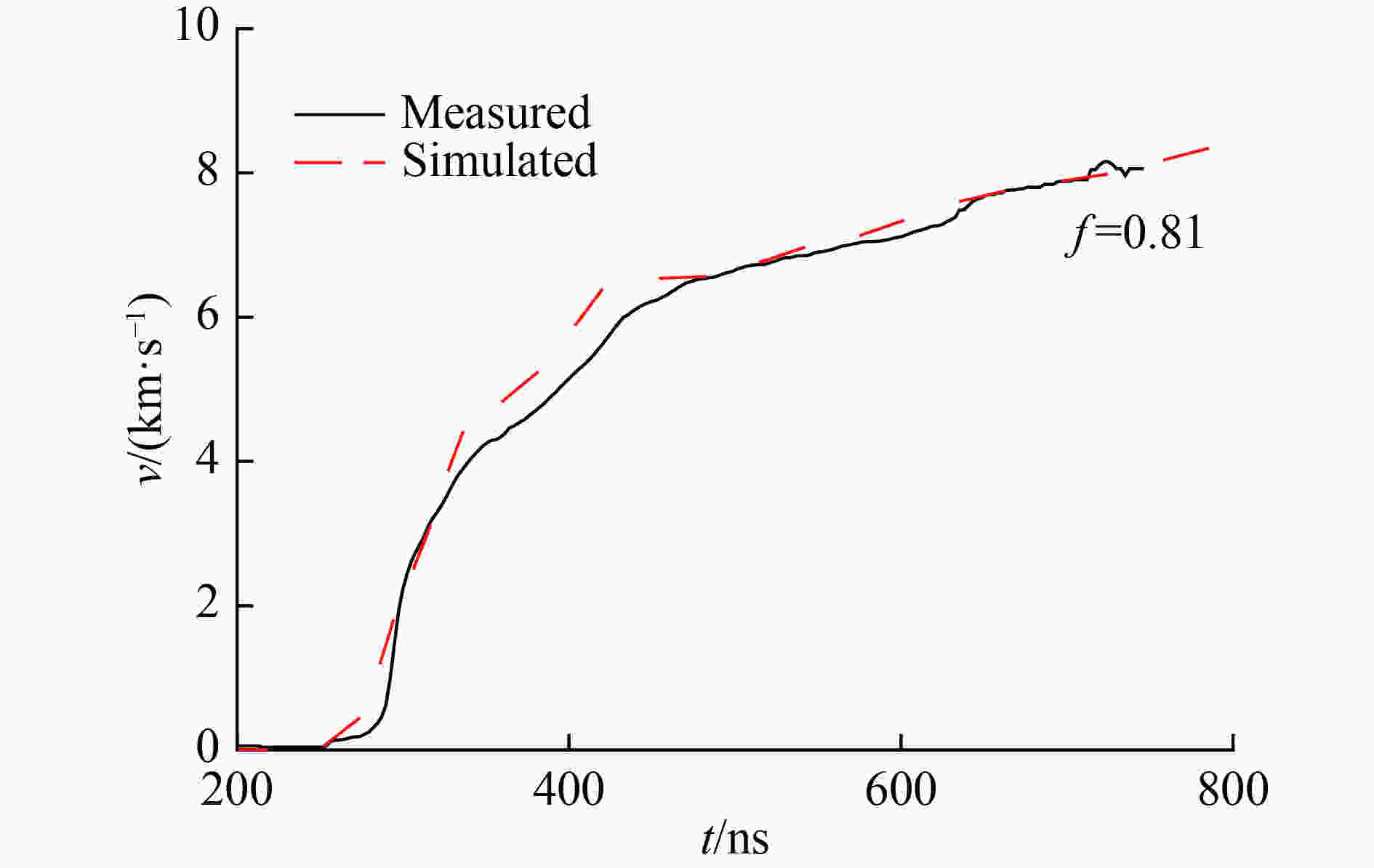
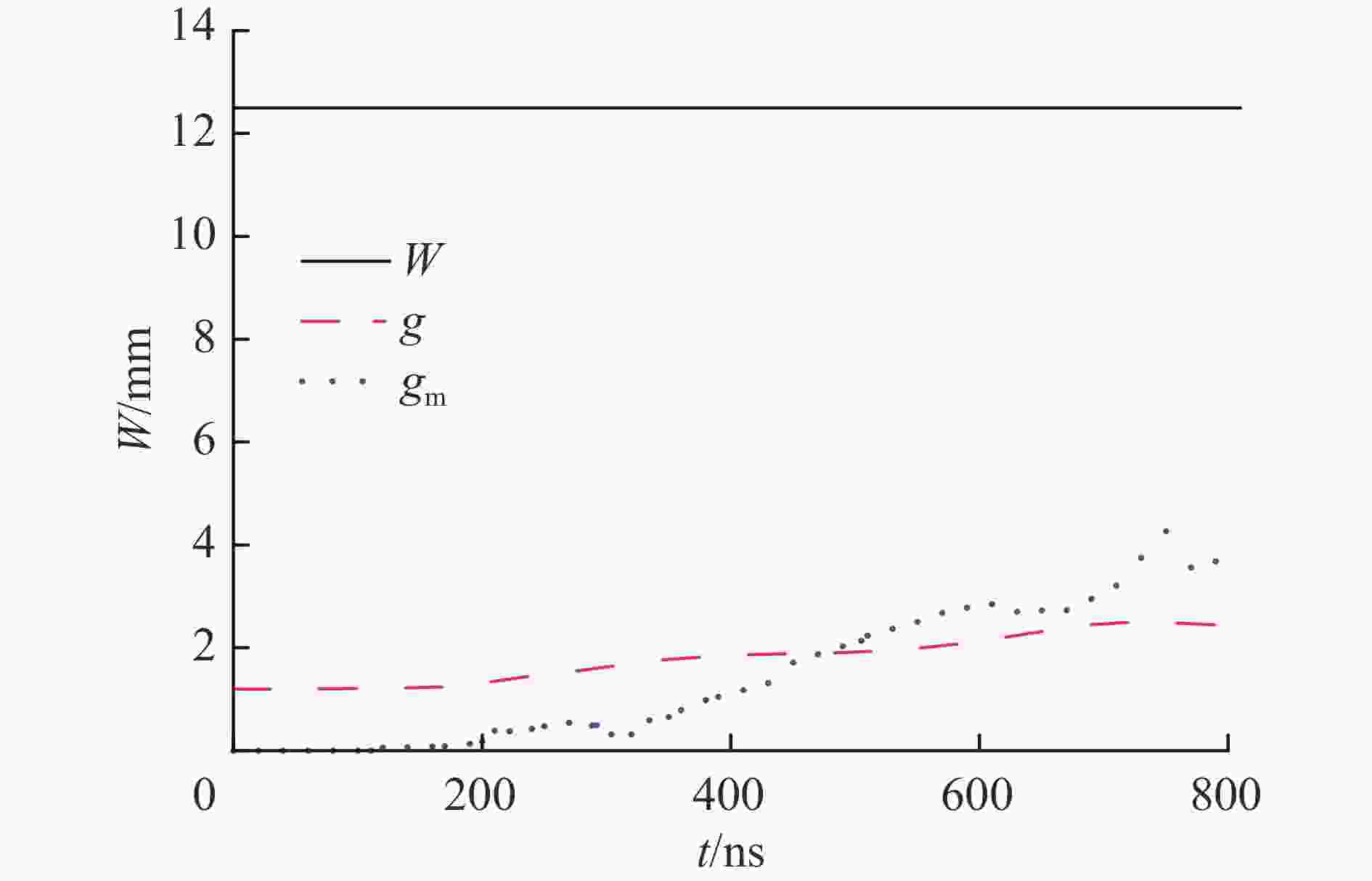
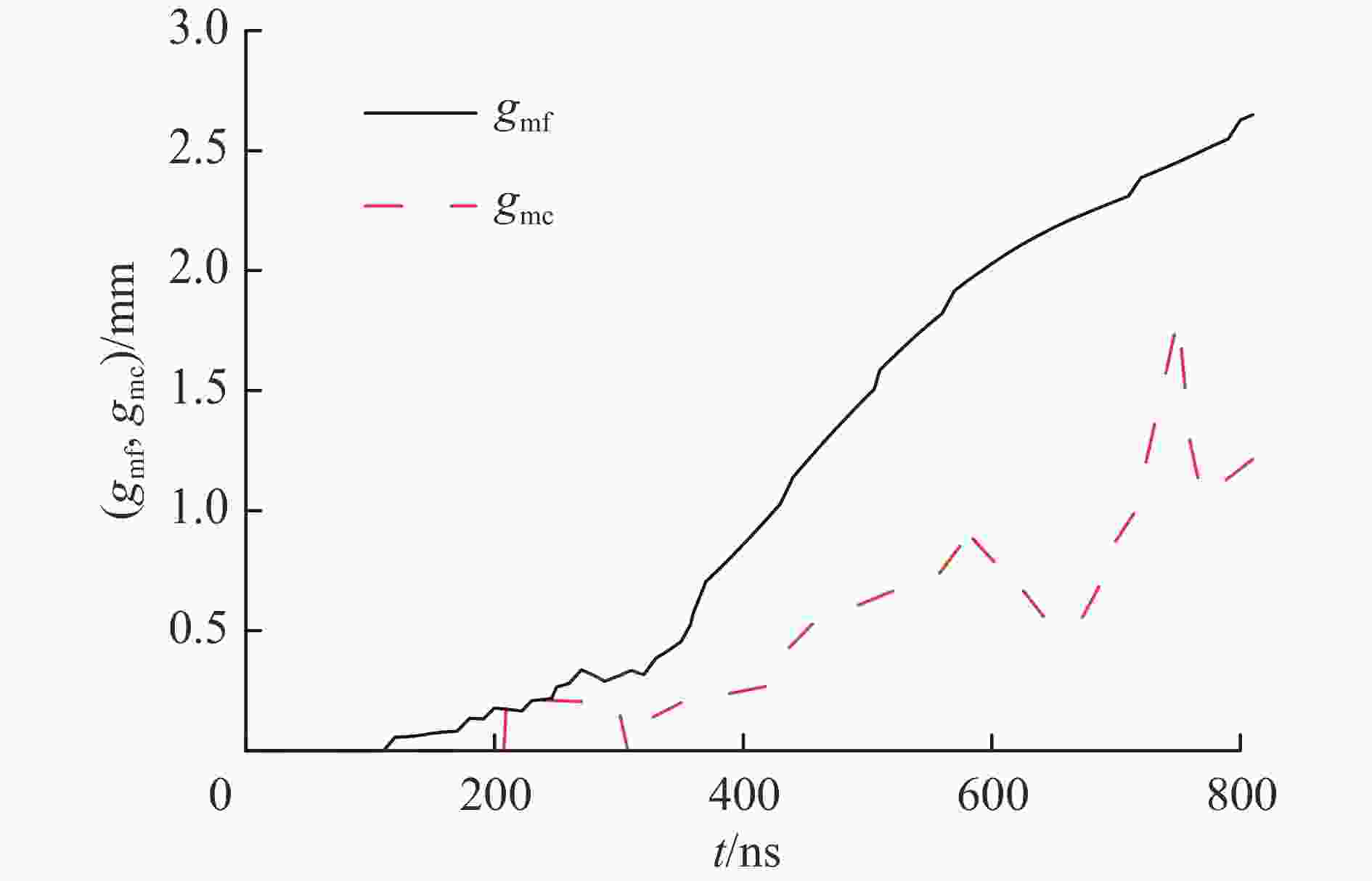
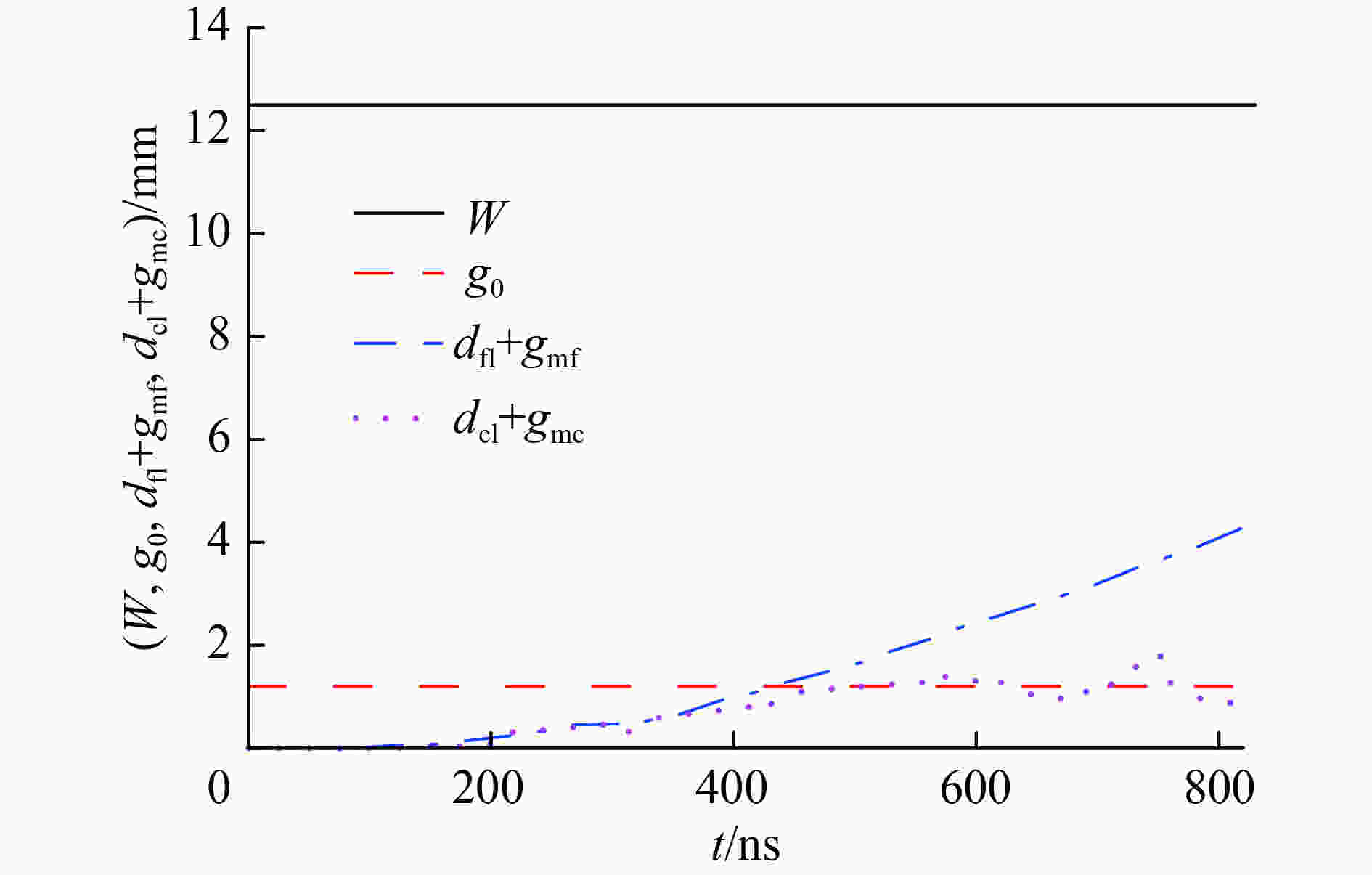
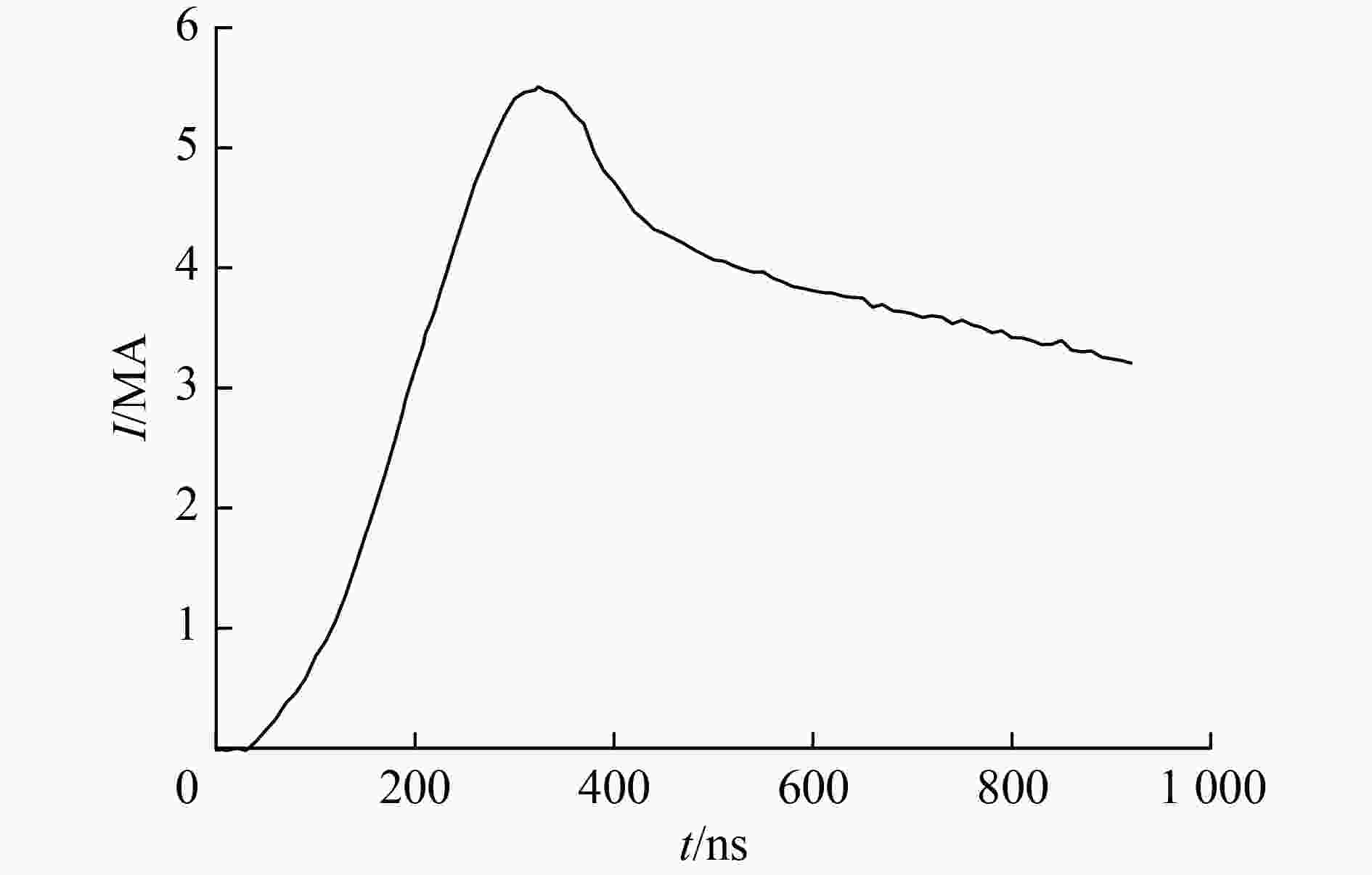
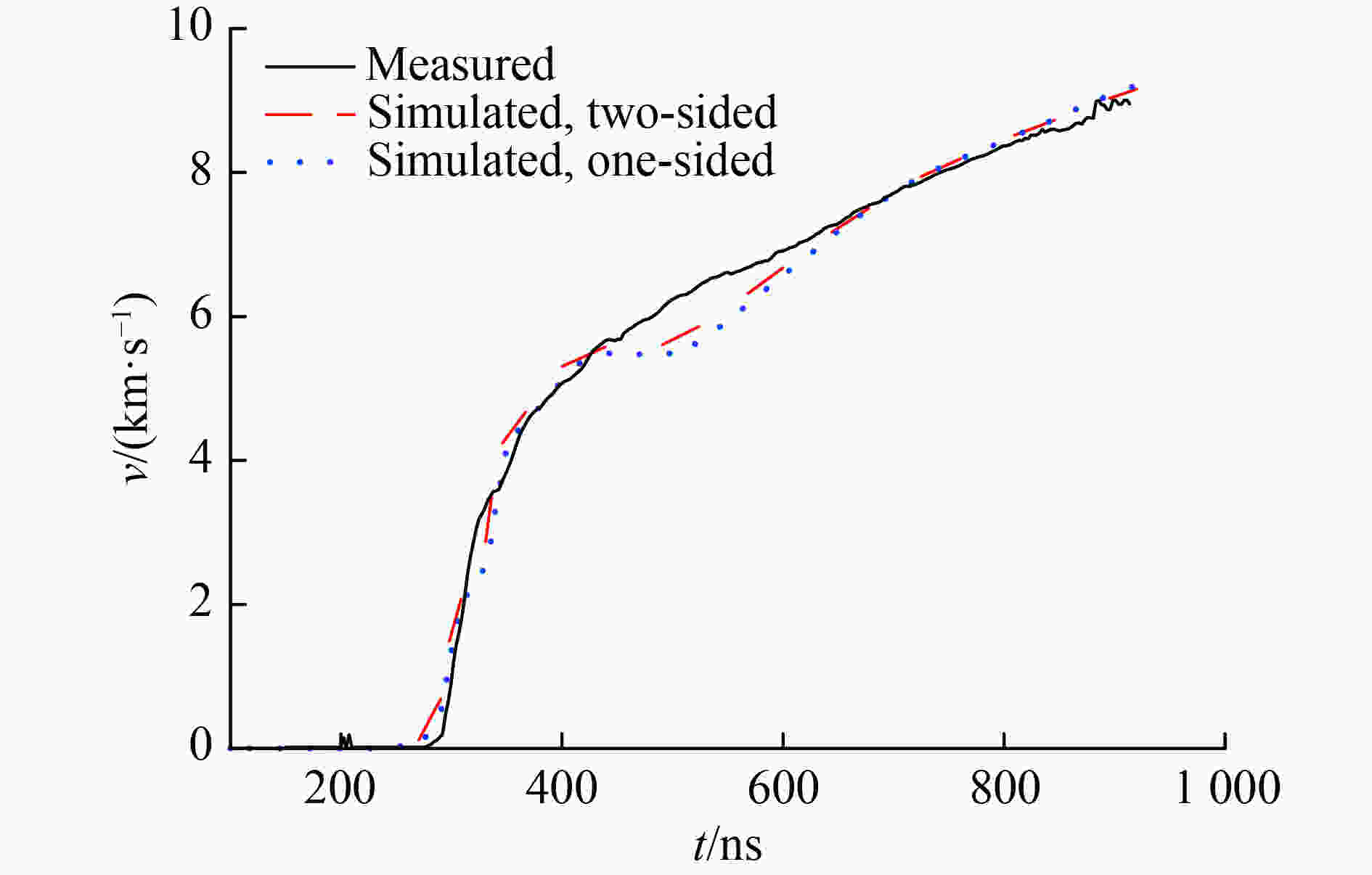
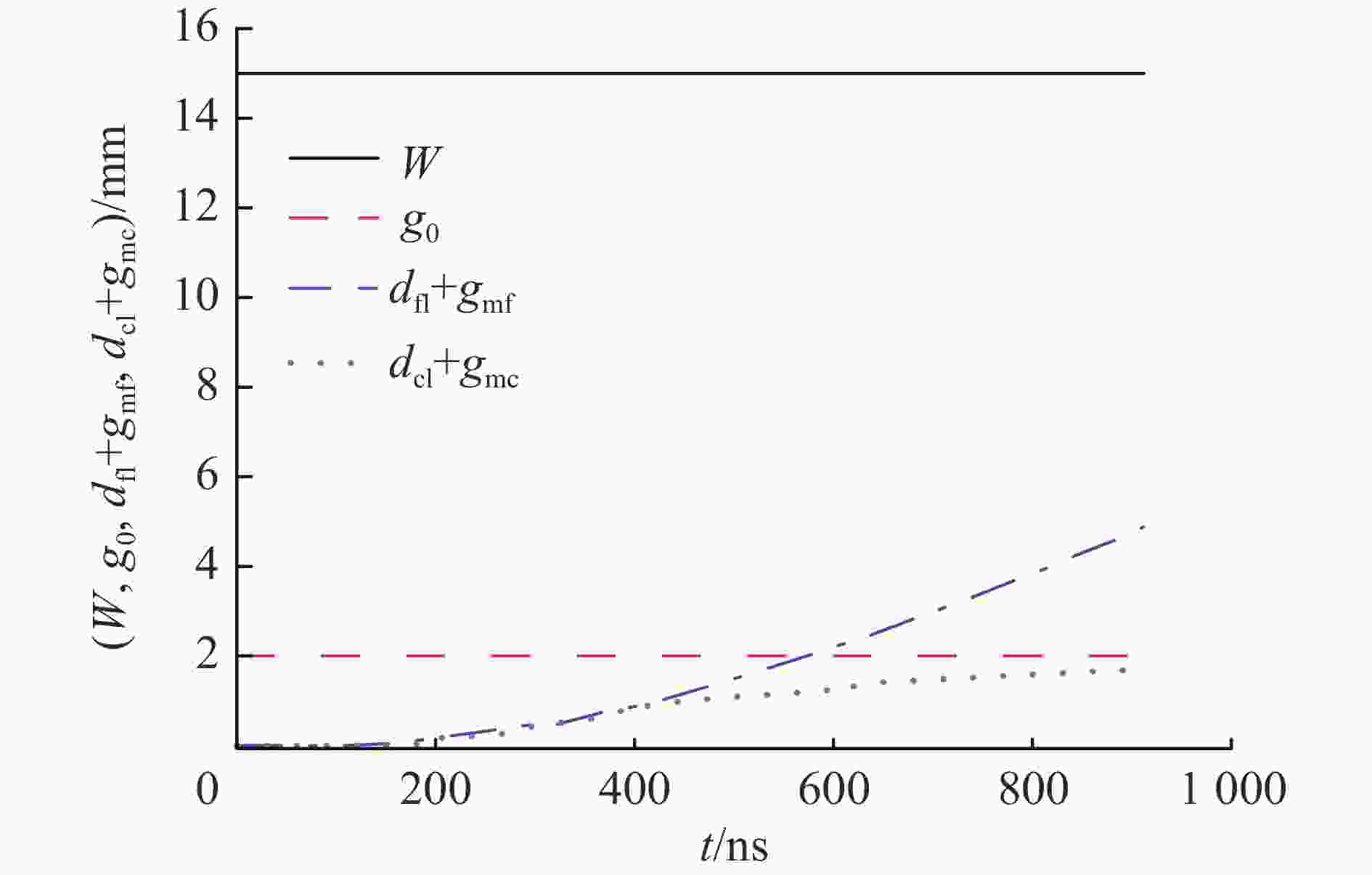
Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China

摘要

摘要: 磁驱动单侧飞片实验的数值模拟通常可不考虑厚的阴极的运动状态和厚度方向上烧蚀宽度的影响，采用单侧计算模型进行模拟。为了理解磁驱动单侧飞片实验可采用单侧计算模型的原因，为磁驱动单侧飞片实验的单侧计算建模提供理论依据，建立了磁驱动单侧飞片实验的双侧计算模型，并对PTS-061、PTS-064磁驱动单侧飞片实验进行了模拟分析。在PTS-061、PTS-064实验中，飞片的电流加载面的位移随着时间的增加持续增大；厚的阴极的电流加载面的位移不随时间的增加持续增大，在磁驱动实验中后期基本保持不变。PTS-061实验结束时，飞片的电流加载面的位移为4.9 mm，阴极电流加载面的位移仅为1.7 mm。PTS-064实验结束时，飞片的电流加载面的位移为4.1 mm，阴极电流加载面的位移仅为0.9 mm。磁驱动单侧飞片实验能采用单侧计算模型模拟的原因，不是阴极板面保持位置不动，而是阴极电流加载面的位移不随时间持续增加；在磁驱动实验后期，飞片电流加载面位移对边界磁场的影响远大于阴极电流加载面的位移对边界磁场的影响。
- 磁驱动单侧飞片实验 /
- 磁流体力学 /
- 单侧计算模型 /
- 自由面速度
Abstract: The numerical simulation of magnetically driven one-sided flyer plate experiment usually does not take into account the influences of cathode motion and ablation width in the thickness direction on the boundary magnetic field. Hence, one-sided computational model was usually applied to simulate magnetically driven one-sided flyer plate experiment. In order to understand the reason why magnetically driven one-sided flyer plate experiment can be simulated by one-sided computational model, magnetically driven one-sided flyer plate experiment (experiment PTS-061 with a 0.972-mm-thick aluminum flyer plate and experiment PTS-064 with a 1.041-mm-thick aluminum flyer plate) were simulated by two-sided computational model. In the experiments with experiment PTS-061 and PTS-064, displacement of thin flyer plate current-loading surface increases with time; displacement of thick cathode current-loading surface does not increases with time, and remains basically unchanged with small displacement in the middle and late stage of experiments. At the end of experiment PTS-061, displacement of thin flyer plate current-loading surface is 4.9 mm, and displacement of thick cathode current-loading surface is only 1.7 mm. At the end of experiment PTS-064, displacement of thin flyer plate current-loading surface is 4.1 mm, and displacement of thick cathode current-loading surface is only 0.9 mm. The reason of one-sided computational model can be adopted in magnetically driven one-sided flyer plate experiment is not that cathode plate position remains unchanged, but instead that cathode current-loading surface has smaller displacement remaining basically unchanged in the middle and later stage of experiments, and the displacement of thin flyer plate current-loading surface has a greater influence on the boundary magnetic field that of thick cathode current-loading surface in the late stage of experiments.
- magnetically driven one-sided flyer plate experiment /
- magneto-hydrodynamics /
- one-sided computational model /
- free-surface velocity

HTML全文

图 1 PTS-061实验的磁驱动负载结构

Figure 1. Cross section of 3D flyer configuration

下载: 全尺寸图片幻灯片

图 2 单侧计算模型

Figure 2. One-sided computational model

下载: 全尺寸图片幻灯片

图 3 PTS-064实验的电流

Figure 3. Current of experiment PTS-064

下载: 全尺寸图片幻灯片

图 4 PTS-064实验飞片自由面速度的单侧计算结果

Figure 4. Flyer plate free-surface velocities of experiment PTS-064 simulated by one-sided computational model

下载: 全尺寸图片幻灯片

图 5 PTS-064实验真空间隙和飞片烧蚀宽度的单侧计算结果

Figure 5. Vacuum gap and flyer-plate ablation depth of experiment PTS-064 simulated by one-sided computational model

下载: 全尺寸图片幻灯片

图 6 双侧计算模型

Figure 6. Two-sided computational model

下载: 全尺寸图片幻灯片

图 7 PTS-064实验飞片自由面速度的双侧计算结果

Figure 7. Flyer plate free-surface velocities of experiment PTS-064 simulated by two-sided computational model

下载: 全尺寸图片幻灯片

图 8 PTS-064实验真空间隙和飞片烧蚀宽度的双侧计算结果

Figure 8. Vacuum gap and flyer plate ablation depth of experiment PTS-064 simulated by two-sided computational model

下载: 全尺寸图片幻灯片

图 9 PTS-064实验飞片和阴极烧蚀厚度的双侧计算结果

Figure 9. Flyer plate and cathode ablation depths of experiment PTS-064 simulated by two-sided computational model

下载: 全尺寸图片幻灯片

图 10 PTS-064实验飞片和阴极电流加载面位移的双侧计算结果

Figure 10. Displacements of flyer plate and cathode current-loading surfaces of experiment PTS-064 simulated by two-sided computational model

下载: 全尺寸图片幻灯片

图 11 PTS-061实验的电流

Figure 11. Current of experiment PTS-061

下载: 全尺寸图片幻灯片

图 12 PTS-061实验飞片自由面速度的单、双侧计算结果

Figure 12. Flyer plate free-surface velocities of experiment TS-061 simulated by one-sided and two-sided computational models

下载: 全尺寸图片幻灯片

图 13 PTS-061实验飞片和阴极电流加载面位移的双侧计算结果

Figure 13. Displacements of flyer plate and cathode current-loading surfaces of experiment PTS-061 simulated by two-sided computational model

下载: 全尺寸图片幻灯片

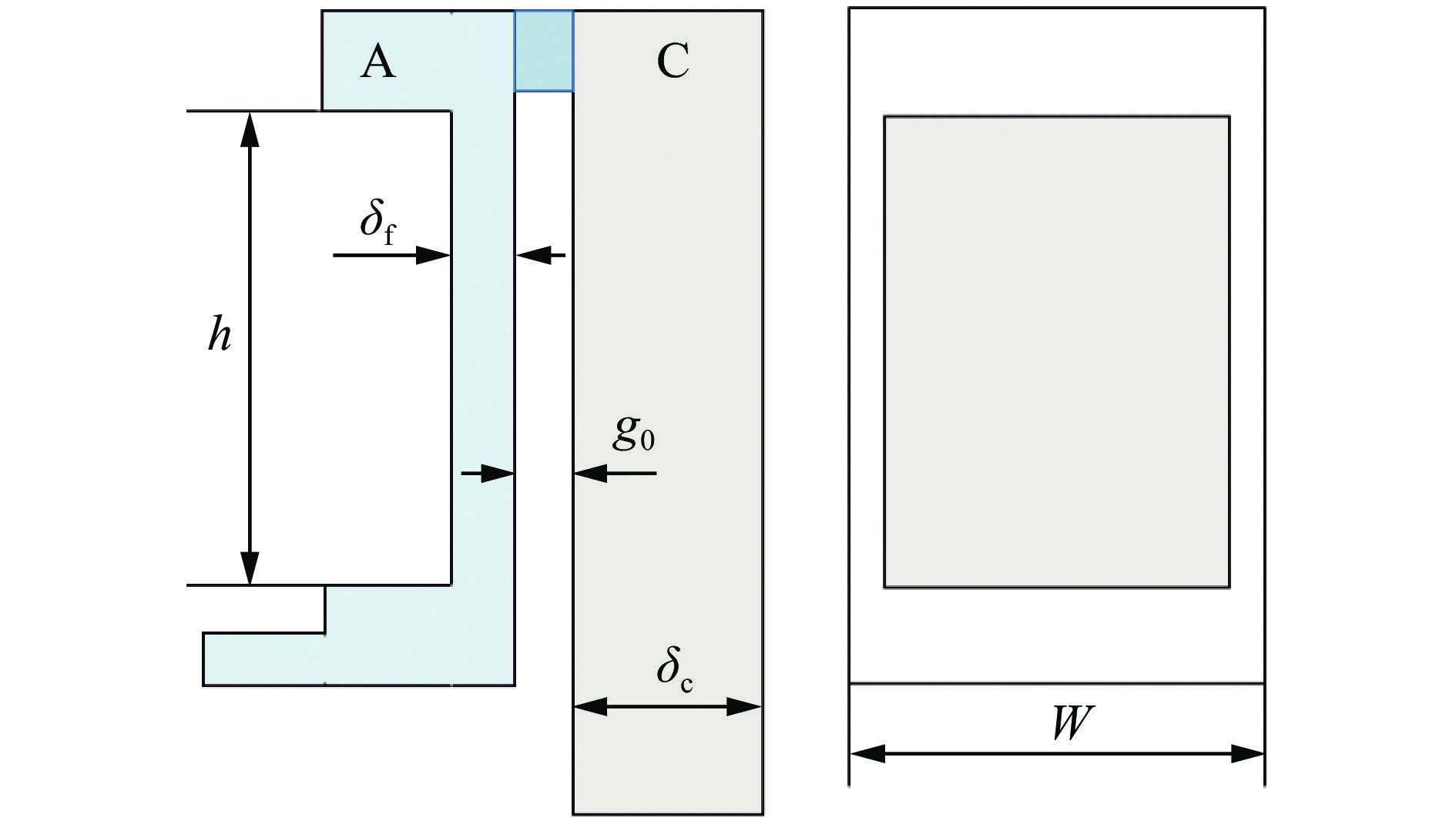
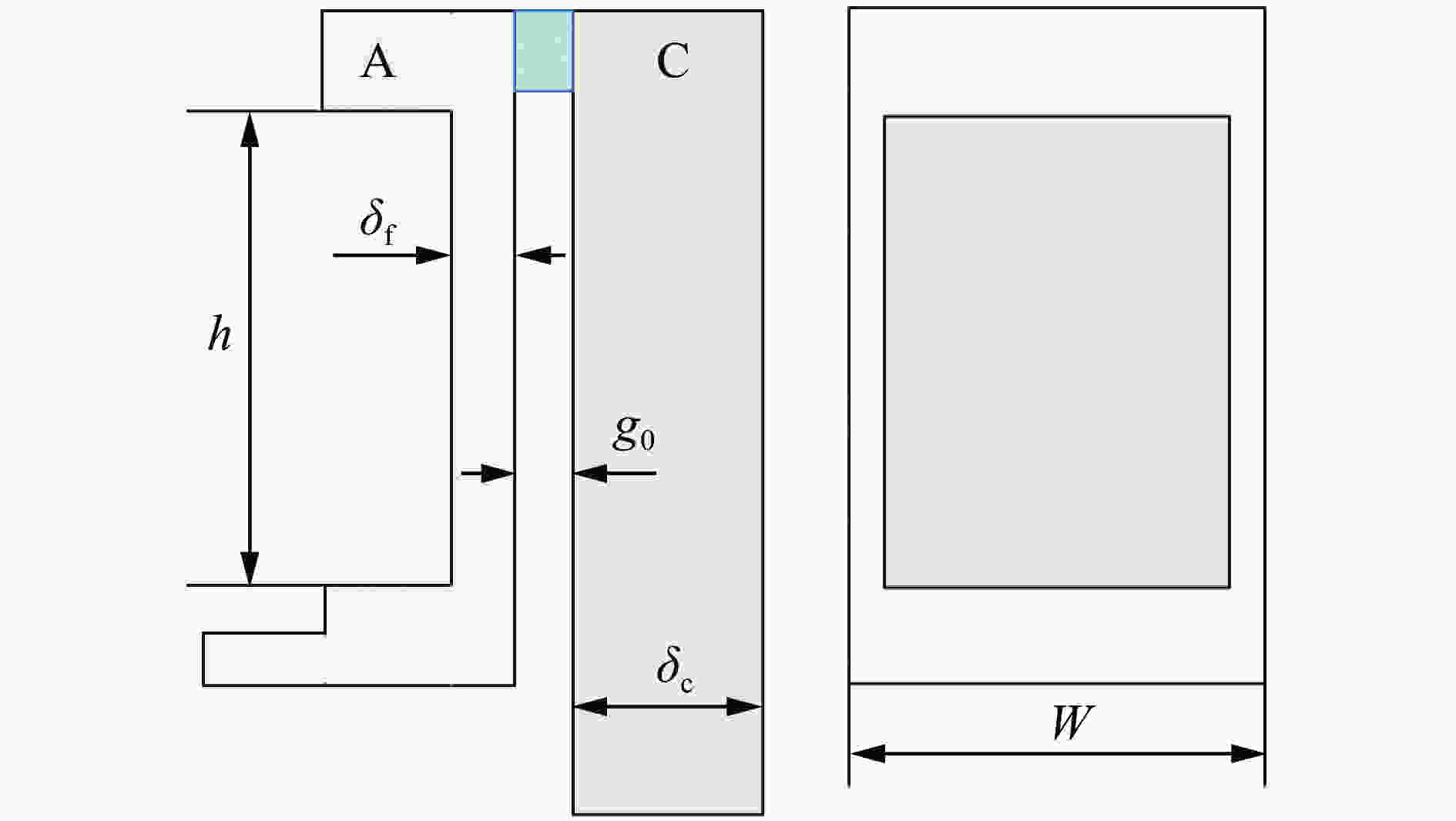
表 1 磁驱动单侧飞片实验的负载参数

Table 1. Loading parameters for magnetically driven one-sided flyer plate experiments

实验 ${\delta _{\rm{f}}}$/mm ${\delta _{\rm{c}}}$/mm ${g_0}$/mm W/mm

PTS-061 0.972 5 2.0 15.0
PTS-064 1.041 5 1.2 12.5

下载: 导出CSV

参考文献(19)

[1]	KNUDSON M D, LEMKE R W, HAYES D B, et al. Near-absolute Hugoniot measurements in aluminum to 500 GPa using a magnetically accelerated flyer plate technique [J]. Journal of Applied Physics, 2003, 94(7): 4420–4431. DOI: 10.1063/1.1604967.
[2]	LEMKE R W, KNUDSON M D, BLISS D E, et al. Magnetically accelerated, ultrahigh velocity flyer plates for shock wave experiments [J]. Journal of Applied Physics, 2005, 98: 073530. DOI: 10.1063/1.2084316.
[3]	KNUDSON M D, HANSON D L, BAILEY J E, et al. Equation of state measurements in liquid Deuterium to 70 GPa [J]. Physical Review Letters, 2001, 87: 225501. DOI: 10.1103/PhysRevLett.87.225501.
[4]	KNUDSON M D, HANSON D L, BAILEY J E, et al. Use of a wave reverberation technique to infer the density compression of shocked liquid deuterium to 75 GPa [J]. Physical Review Letters, 2003, 90: 035505. DOI: 10.1103/PhysRevLett.90.035505.
[5]	KNUDSON M D, HANSON D L, BAILEY J E, et al. Principal Hugoniot, reverberating wave, and mechanical reshock measurements of liquid deuterium to 400 GPa using plate impact techniques [J]. Physical Review B, 2004, 69: 144209. DOI: 10.1103/PhysRevB.69.144209.
[6]	LEMKE R W, KNUDSON M D, HALL C A, et al. Characterization of magnetically accelerated flyer plates [J]. Physics of Plasmas, 2003, 10(4): 1092–1099. DOI: 10.1063/1.1554740.
[7]	LEMKE R W, KNUDSON M D, DAVIS J P. Magnetically driven hyper-velocity launch capability at the Sandia Z accelerator [J]. International Journal of Impact Engineering, 2011, 38(6): 480–485. DOI: 10.1016/j.ijimpeng.2010.10.019.
[8]	DAVIS J P, BROWN J L, KNUDSON M D, et al. Analysis of shockless dynamic compression data on solids to multi-megabar pressures: application to tantalum [J]. Journal of Applied Physics, 2014, 116: 204903. DOI: 10.1063/1.4902863.
[9]	KAN M X, ZHANG Z H, XIAO B, et al. Simulation of magnetically driven flyer plate experiments with an improved magnetic field boundary formula [J]. High Energy Density Physics, 2018, 26: 38–43. DOI: 10.1016/j.hedp.2017.12.002.
[10]	DENG J J, XIE W P, FENG S P, et al. Initial performance of the Primary Test Stand [J]. IEEE TPS, 2013, 41(10): 2580–2583.
[11]	但加坤, 任晓东, 黄显宾, 等. Z箍缩内爆产生的电磁脉冲辐射 [J]. 物理学报, 2013, 62(24): 245201. DOI: 10.7498/aps.62.245201. DAN J K, REN X D, HUANG X B, et al. Electromagnetic pulse emission produced by Z pinch implosions [J]. Acta Physica Sinica, 2013, 62(24): 245201. DOI: 10.7498/aps.62.245201.
[12]	郭帅, 王贵林, 张朝辉, 等. 聚龙一号装置准等熵压缩实验负载优化研究 [J]. 强激光与粒子束, 2016, 28(1): 015015. DOI: 10.11884/HPLPB201628.015015. GUO S, WANG G L, ZHANG Z H, et al. Optimization of load configurations for isentropic compression experiments on PTS [J]. High Power Laser and Particle Beams, 2016, 28(1): 015015. DOI: 10.11884/HPLPB201628.015015.
[13]	王贵林, 张朝辉, 郭帅, 等. 聚龙一号装置上铜的准等熵压缩线测量实验研究 [J]. 强激光与粒子束, 2016, 28(5): 055010. DOI: 10.11884/HPLPB201628.055010. WANG G L, ZHANG Z H, GUO S, et al. Experimental measurement of quasi-isentrope for copper on PTS [J]. High Power Laser and Particle Beams, 2016, 28(5): 055010. DOI: 10.11884/HPLPB201628.055010.
[14]	阚明先, 蒋吉昊, 王刚华, 等. 套筒内爆ALE方法二维MHD数值模拟 [J]. 四川大学学报, 2007, 44(1): 91–96. DOI: 10.3969/j.issn.0490-6756.2007.01.020. KAN M X, JIANG J H, WANG G H, et al. ALE simulation 2D MHD for liner [J]. Journal of Sichuan University, 2007, 44(1): 91–96. DOI: 10.3969/j.issn.0490-6756.2007.01.020.
[15]	阚明先, 王刚华, 赵海龙, 等. 磁驱动飞片二维磁流体力学数值模拟 [J]. 强激光与粒子束, 2013, 25(8): 2137–2141. DOI: 10.3788/HPLPB20132508.2137. KAN M X, WANG G H, ZHAO H L, et al. Two dimensional magneto-hydrodynamic simulations of magnetically accelerated flyer plates [J]. High Power Laser and Particle Beams, 2013, 25(8): 2137–2141. DOI: 10.3788/HPLPB20132508.2137.
[16]	杨龙, 王刚华, 阚明先, 等. 基于MDSC程序的Z箍缩内爆单温和三温模拟分析 [J]. 高压物理学报, 2016, 30(1): 64–70. DOI: 10.11858/gywlxb.2016.01.010. YANG L, WANG G H, KAN M X, et al. A numerical simulation analysis of mono-temperature and tri-temperature models by MDSC program Z-pinch implosion [J]. Chinese Journal of High Pressure Physics, 2016, 30(1): 64–70. DOI: 10.11858/gywlxb.2016.01.010.
[17]	阚明先, 张朝辉, 段书超, 等. “聚龙一号”装置上磁驱动铝飞片实验的数值模拟 [J]. 强激光与粒子束, 2015, 27(12): 125001. DOI: 10.11884/HPLPB201527.125001. KAN M X, ZHANG Z H, DUAN S C, et al. Numerical simulation of magnetically driven aluminum flyer plate on PTS accelerator [J]. High Power Laser and Particle Beams, 2015, 27(12): 125001. DOI: 10.11884/HPLPB201527.125001.
[18]	阚明先, 段书超, 王刚华, 等. 自由面被烧蚀磁驱动飞片的数值模拟 [J]. 强激光与粒子束, 2017, 29(4): 045003. DOI: 10.11884/HPLPB201729.160482. KAN M X, DUAN S C, WANG G H, et al. Numerical simulation of magnetically driven flyer plate of ablated free surface [J]. High Power Laser and Particle Beams, 2017, 29(4): 045003. DOI: 10.11884/HPLPB201729.160482.
[19]	阚明先, 王刚华, 赵海龙, 等. 金属电阻率模型 [J]. 爆炸与冲击, 2013, 33(3): 282–286. DOI: 10.11883/1001-1145(2013)03-0282-05. KAN M X, WANG G H, ZHAO H L, et al. Electrical resistivity model for metals [J]. Explosion and Shock Waves, 2013, 33(3): 282–286. DOI: 10.11883/1001-1145(2013)03-0282-05.