Multi-scale failure mechanism analysis of layered phyllite subject to impact loading
-
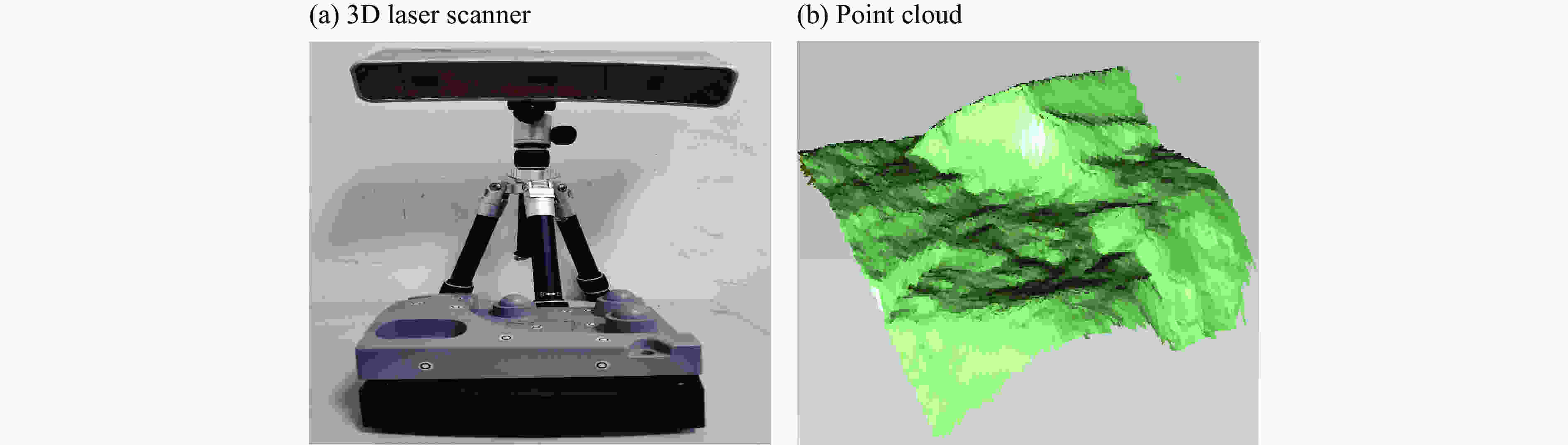
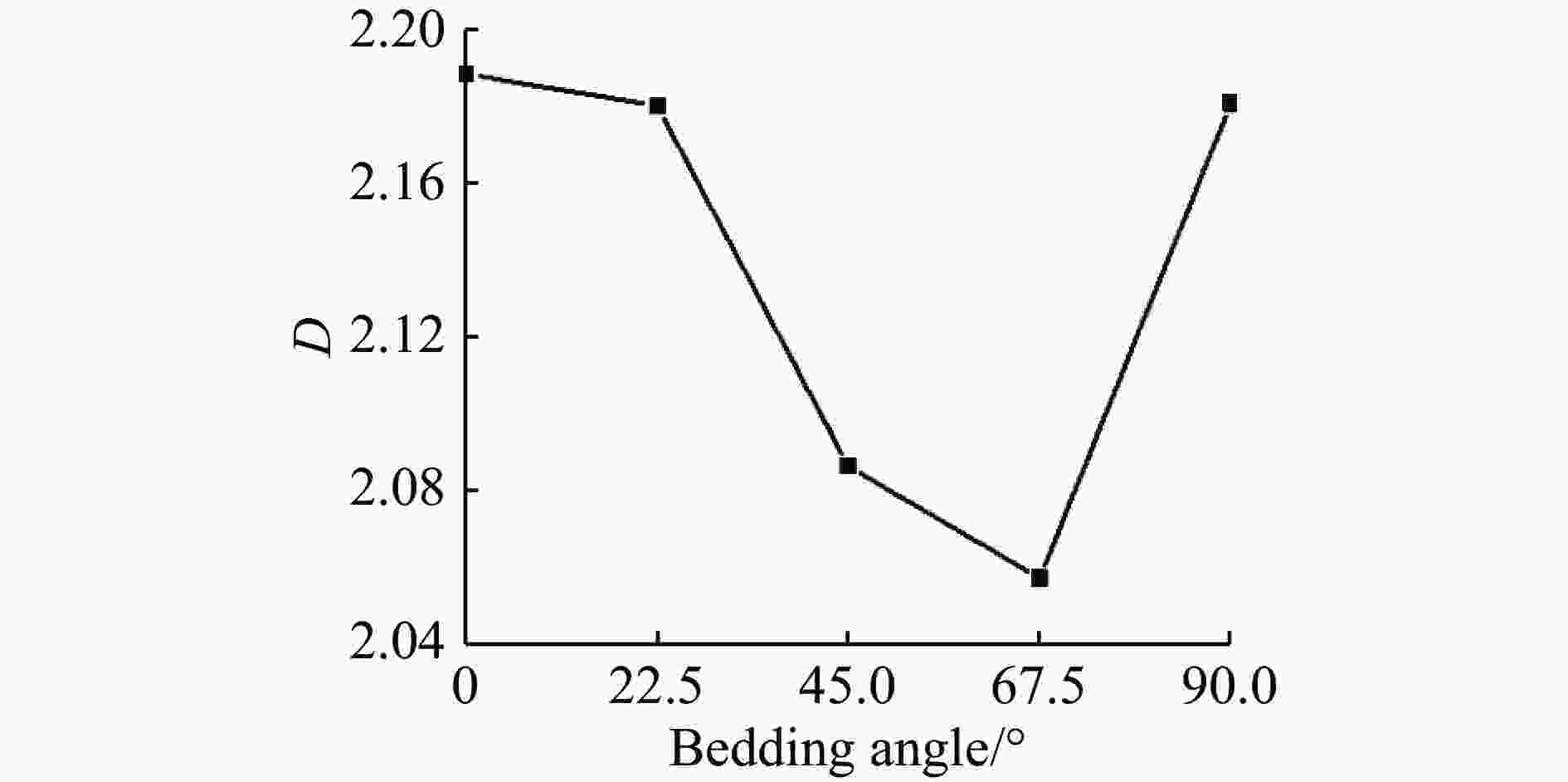
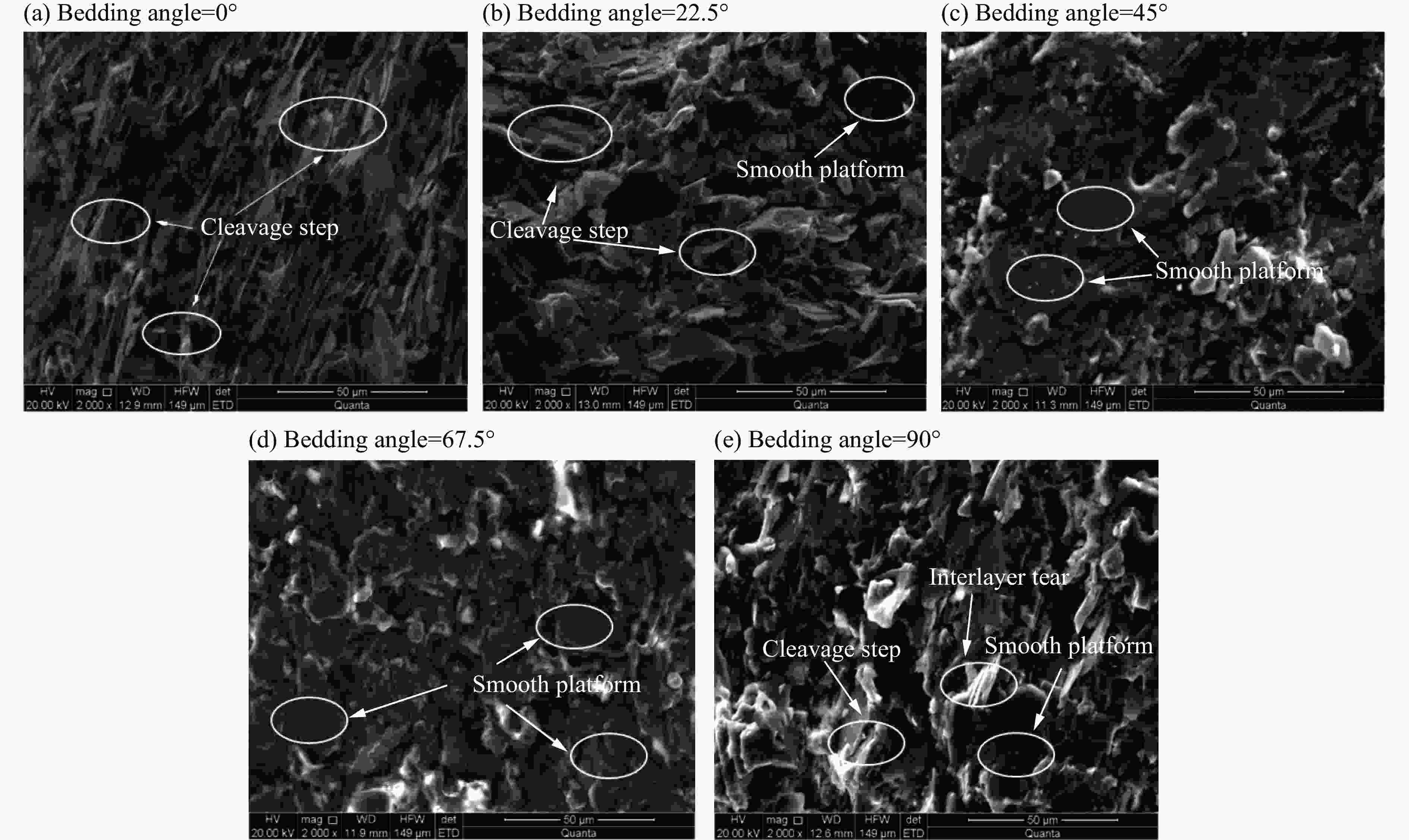
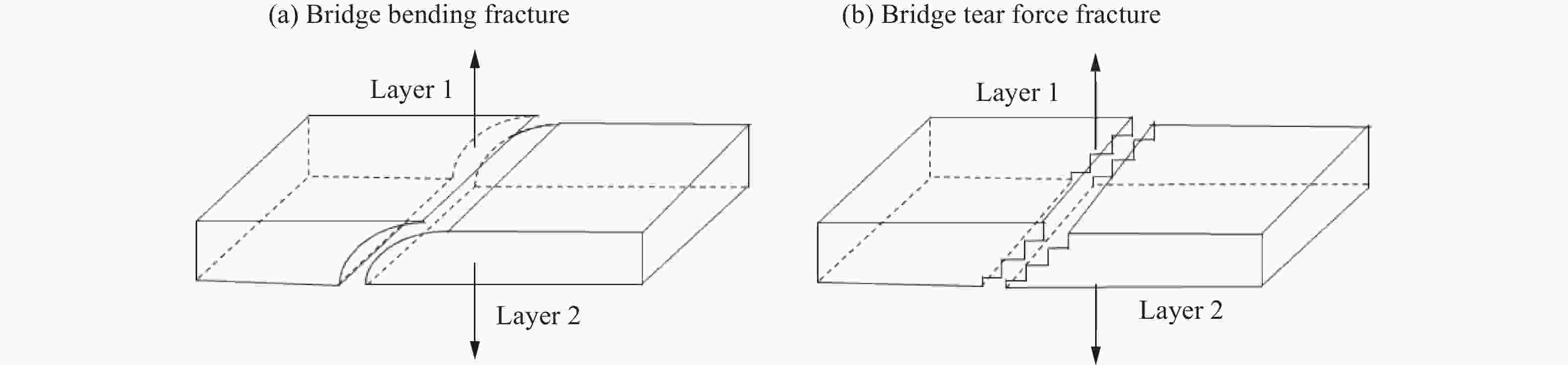
摘要: 通过分离式霍普金森杆对层状千枚岩施加动态载荷,得到不同层理倾角下层状千枚岩的动态抗压强度与宏观破坏模式。采用三维激光仪获得断裂面细观形貌,引入分形几何定量计算断口面粗糙度;结合SEM观察到的微观尺度下不同层理倾角断口破坏机理,分析了不同层理倾角下层状岩石的动态破坏机制。研究结果表明:动态压缩下层理弱面对岩石的抗压强度影响较大;不同层理倾角千枚岩的断口形貌分形维数随层理倾角增大呈U型变化;从强度与裂纹扩展两方面考虑层理弱面对层状岩石破坏特征的影响,对于层理倾角为0°的试样,强度由岩石基质控制,但层理弱面仍对岩石破坏的裂纹分布与走向产生较大影响;对于层理倾角为22.5°的试样,强度与裂纹走向受岩石基质与层理弱面共同控制;对于层理倾角为45°~67.5°的试样,强度与裂纹走向受层理弱面控制;而对于层理倾角为90°的试样,动态抗压强度受岩石基质的影响较大,在层理弱面较早形成纵向宏观裂纹,导致该层理弱面角度下裂纹受层理弱面的影响较大。Abstract: The dynamic compressive strength characteristics and macroscopic failure modes of layered phyllite are carried out by the Split Hopkinson Pressure Bar. The micromorphology of fracture surface was obtained by 3D laser instrument, and the fractal geometry was introduced to quantitatively describe the roughness of fracture surface. Based on the fracture mechanism observed by SEM, the dynamic failure mechanism of layered rock with different bedding angles is analyzed. The results indicate that the weak bedding plane has a great influence on the dynamic compressive strength of layered rock. The fractal dimension of layered phyllite changes in U-shape with the increase of bedding angle. The influence of bedding plane on the failure characteristics of layered rocks is examined according to strength and crack propagation. For specimens with bedding angle of 0°, the failure strength is controlled by rock matrix, but the weak bedding plane still has a large impact on the distribution and trend of cracks in rock failure. For specimens with bedding angle of 22.5°, strength and direction of cracks are controlled by both the rock matrix and weak bedding plane. For specimens with bedding dip angle ranging from 45° to 67.5°, strength and direction of cracks are controlled by weak bedding plane. For the bedding angle of 90°, the dynamic compressive strength of the specimen is affected by the rock matrix, and longitudinal macro-cracks are formed early on the weak plane of the bedding, which results in that the cracks are greatly affected by the bedding plane.
-
Key words:
- impact loads /
- layered phyllite /
- multi-scale /
- fractal dimension
-
表 1 SHPB试验结果
Table 1. Experimental results of SHPB tests
层理倾角/(°) 冲击速度/(m∙s−1) 应变率/s−1 峰值应变率/s−1 峰值应力/MPa 0 14.82 80.18 114.54 247.95 0 14.97 88.35 118.96 254.47 0 14.86 82.28 123.84 241.75 22.5 14.82 91.43 120.64 215.64 22.5 14.96 97.39 127.95 221.35 22.5 14.79 94.48 130.14 206.74 45 14.97 136.73 173.88 148.42 45 14.84 132.50 166.84 142.86 45 14.89 129.95 161.29 138.24 67.5 14.72 140.09 178.73 121.89 67.5 14.74 135.73 173.38 118.83 67.5 14.94 141.48 184.87 126.89 90 14.83 134.60 172.64 185.90 90 14.85 136.95 176.95 197.73 90 14.98 130.74 163.10 177.43 -
[1] JAEGER J C. Shear failure of anisotropic rocks [J]. Geological Magazine, 1960, 97(1): 65–72. DOI: 10.1017/S0016756800061100. [2] 吴亮, 李凤, 卢文波, 等. 爆破扰动下邻近层状围岩隧道的稳定性与振速阈值 [J]. 爆炸与冲击, 2017, 37(2): 208–214. DOI: 10.11883/1001-1455(2017)02-0208-07.WU Liang, LI Feng, LU Wenbo, et al. Vibration velocity threshold of a tunnel adjacent to surrounding layered rocks under blasting load [J]. Explosion And Shock Waves, 2017, 37(2): 208–214. DOI: 10.11883/1001-1455(2017)02-0208-07. [3] POTYONDY O D. The bonded-particle model as a tool for rock mechanics research and application: current trends and future directions [J]. Geosystem Engineering, 2015, 18(1): 1–28. DOI: 10.1080/12269328.2014.998346. [4] 裴建良, 苏立, 刘建锋, 等. 层状大理岩间接拉伸试验及断口形貌和断裂机理分析 [J]. 工程科学与技术, 2014, 46(4): 39–45. DOI: 10.15961/j.jsuese.2014.04.002.PEI Jianliang, SU Li, LIU Jianfeng, et al. Indirect tensile test of layered marble and analysis of fracture morphology and mechanism [J]. Advanced Engineering Sciences, 2014, 46(4): 39–45. DOI: 10.15961/j.jsuese.2014.04.002. [5] TIEN Y M, KUO M C, JUANG C H. An experimental investigation of the failure mechanism of simulated transversely isotropic rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(8): 1163–1181. DOI: 10.1016/j.ijrmms.2006.03.011. [6] MA T, PENG N, ZHU Z, et al. Brazilian tensile strength of anisotropic rocks: Review and new insights [J]. Energies, 2018, 11(2): 304. DOI: 10.3390/en11020304. [7] 李先炜, 兰勇瑞, 邹俊兴. 岩石断口分析 [J]. 中国矿业学院学报, 1983, 12(1): 15–21.LI Xianwei, LAN Yongrui, ZOU Junxing. A study of rock fractures [J]. Journal of China University of Mining & Technology, 1983, 12(1): 15–21. [8] 谢和平, 陈至达. 断口定量分析的分形几何方法 [J]. 工程力学, 1989, 6(4): 1–8.XIE Heping, CHEN Zhida. The method of fractal geometry for quantitative analysis of fracture surfaces [J]. Engineering Mechanics, 1989, 6(4): 1–8. [9] 王礼立. 爆炸与冲击载荷下结构和材料动态响应研究的新进展 [J]. 爆炸与冲击, 2001, 21(2): 81–88. DOI: 10.3321/j.issn:1001-1455.2001.02.001.WANG Lili. Progress in studies on dynamic response of structures and materials under explosive/impact loading [J]. Explosion and Shock Waves, 2001, 21(2): 81–88. DOI: 10.3321/j.issn:1001-1455.2001.02.001. [10] LI X F, ZHANG Q B, LI H B, et al. Grain-based discrete element method (GB-DEM) modelling of multi-scale fracturing in rocks under dynamic loading [J]. Rock Mechanics and Rock Engineering, 2018, 51(12): 3785–3817. DOI: 10.1007/s00603-018-1566-2. [11] 李海波, 王建伟, 李俊如, 等. 单轴压缩下软岩的动态力学特性试验研究 [J]. 岩土力学, 2004, 25(1): 1–4. DOI: 10.3969/j.issn.1000-7598.2004.01.001.LI Haibo, WANG Jianwei, LI Junru, et al. Mechanical properties of soft rock under dynamic uniaxial compression [J]. Rock and Soil Mechanics, 2004, 25(1): 1–4. DOI: 10.3969/j.issn.1000-7598.2004.01.001. [12] ZHANG Q B, ZHAO J. Effect of loading rate on fracture toughness and failure micromechanisms in marble [J]. Engineering Fracture Mechanics, 2013, 102: 288–309. DOI: 10.1016/j.engfracmech.2013.02.009. [13] ZHANG Z X, KOU S Q, JIANG L G, et al. Effects of loading rate on rock fracture: fracture characteristics and energy partitioning [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 745–762. DOI: 10.1016/S1365-1609(00)00008-3. [14] ULUSAY R. The ISRM suggested methods for rock characterization, testing and monitoring: 2007-2014 [M]. Berlin: Springer International Publishing, 2014: 35−44. DOI: 10.1007/978-3-319-07713-0 [15] LI X F, LI X, LI H B, et al. Dynamic tensile behaviours of heterogeneous rocks: The grain scale fracturing characteristics on strength and fragmentation [J]. International Journal of Impact Engineering, 2018, 118: 98–118. DOI: 10.1016/j.ijimpeng.2018.04.006. [16] LI X F, LI H B, ZHANG Q B, et al. Dynamic fragmentation of rock material: characteristic size, fragment distribution and pulverization law [J]. Engineering Fracture Mechanics, 2018, 199: 739–759. DOI: 10.1016/j.engfracmech.2018.06.024. [17] 李晓锋, 李海波, 刘凯, 等. 冲击荷载作用下岩石动态力学特性及破裂特征研究 [J]. 岩石力学与工程学报, 2017(10): 57–69. DOI: 10.13722/j.cnki.jrme.2017.0539.LI Xiaofeng, LI Haibo, LIU Kai, et al. Dynamic properties and fracture characteristics of rocks subject to impact loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2017(10): 57–69. DOI: 10.13722/j.cnki.jrme.2017.0539. [18] 张亚衡, 周宏伟, 谢和平. 粗糙表面分形维数估算的改进立方体覆盖法 [J]. 岩石力学与工程学报, 2005(17): 3192–3196. DOI: 10.3321/j.issn:1000-6915.2005.17.030.ZHANG Yaheng, ZHOU Hongwei, XIE Heping. Improved cubic covering method for fractal dimensions of a fracture surface of rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2005(17): 3192–3196. DOI: 10.3321/j.issn:1000-6915.2005.17.030. [19] DEREK H. 断口形貌学[M]. 李晓刚, 董超芳, 杜翠薇, 等译. 北京: 科学出版社, 2009: 93−109. [20] TOLANSKY S. Surface microtophgraphy [M]. London: Longmans, 1960: 78−89. DOI: 10.1021/ja01469a074. [21] TAKAHASHI K. Dynamic fracture instability in glassy polymers as studied by ultrasonic fractography [J]. Polymer Engineering & Science, 2010, 27(1): 25–32. DOI: 10.1002/pen.760270105. -







 下载:
下载: