A GPU parallel staircase finite difference mesh generation algorithm based on the ray casting method
-
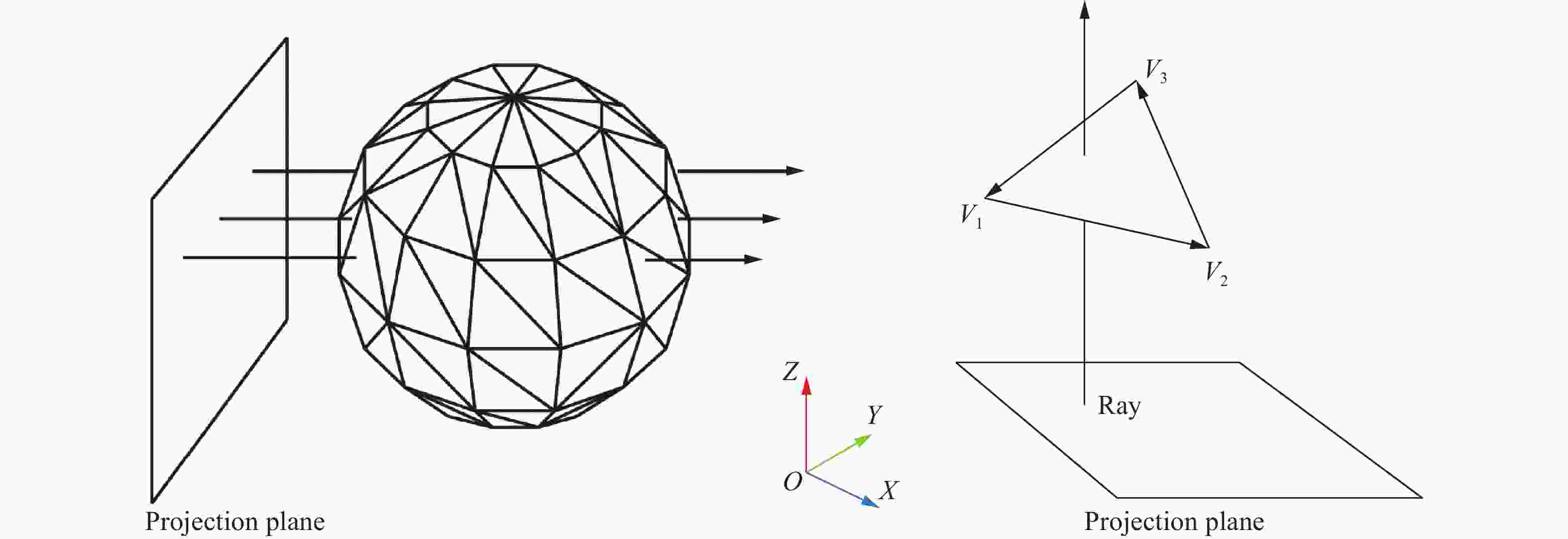
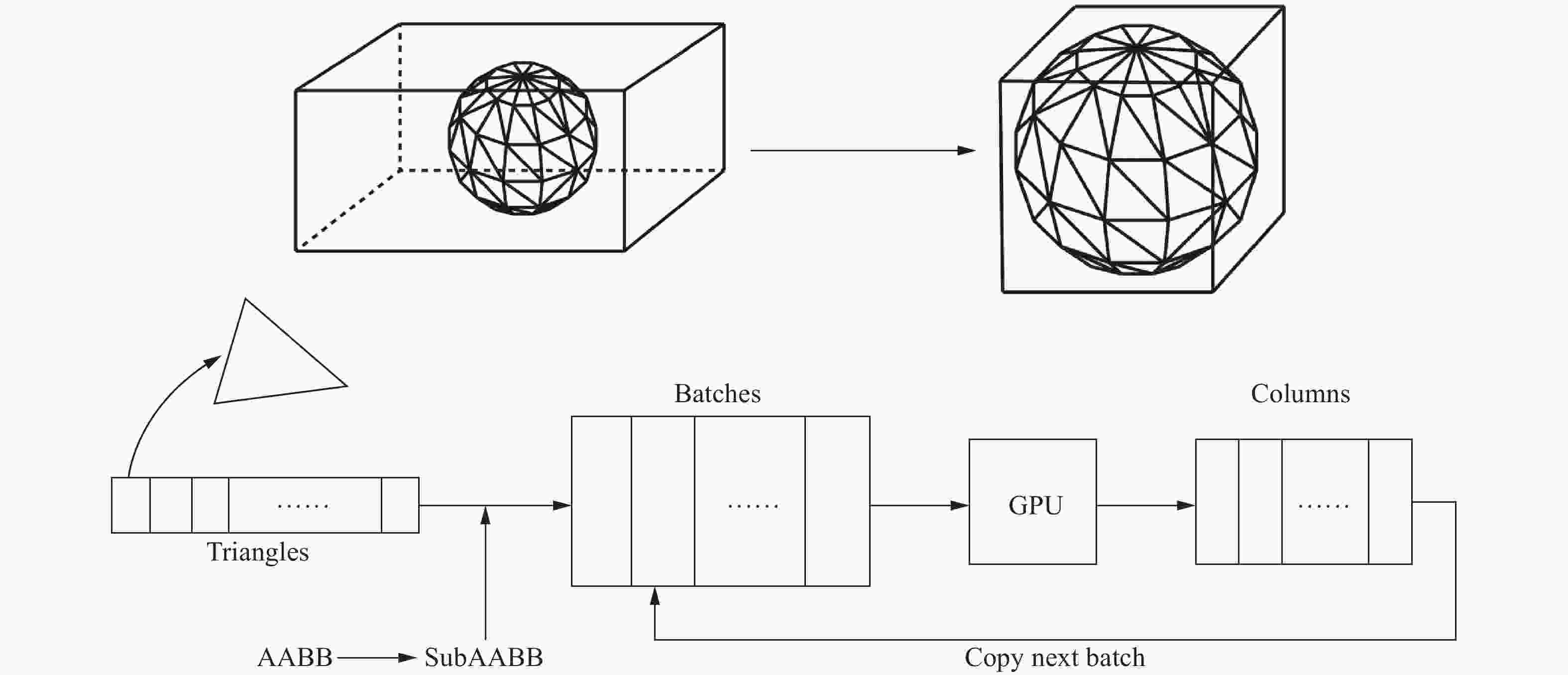
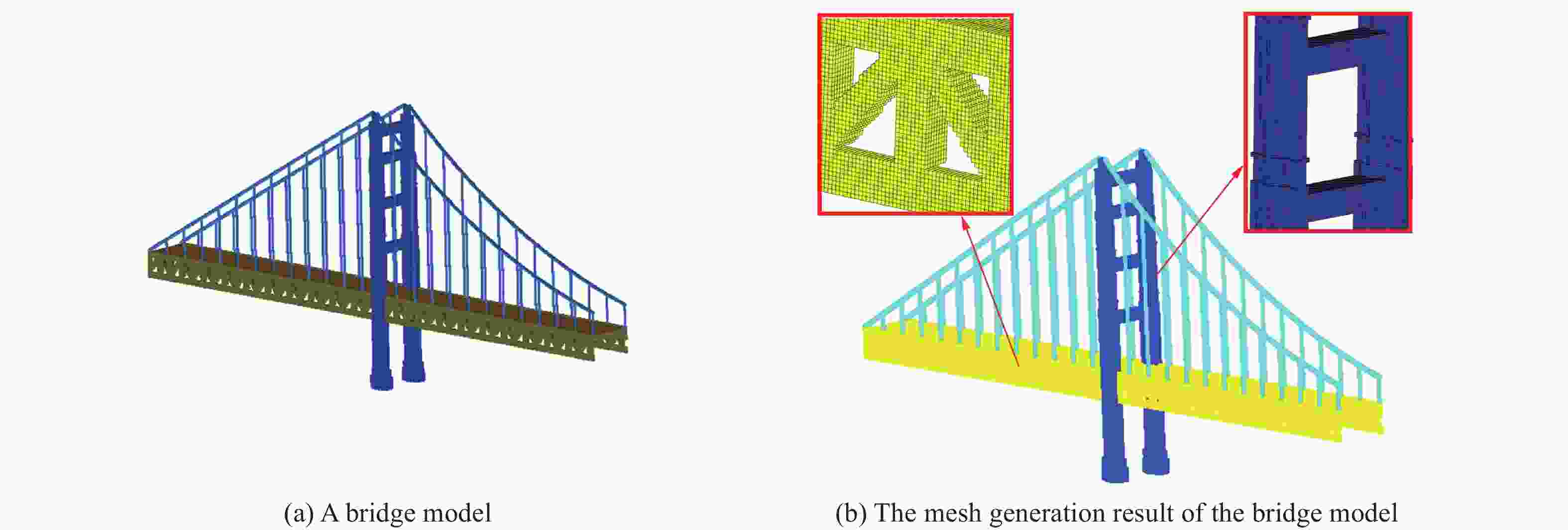
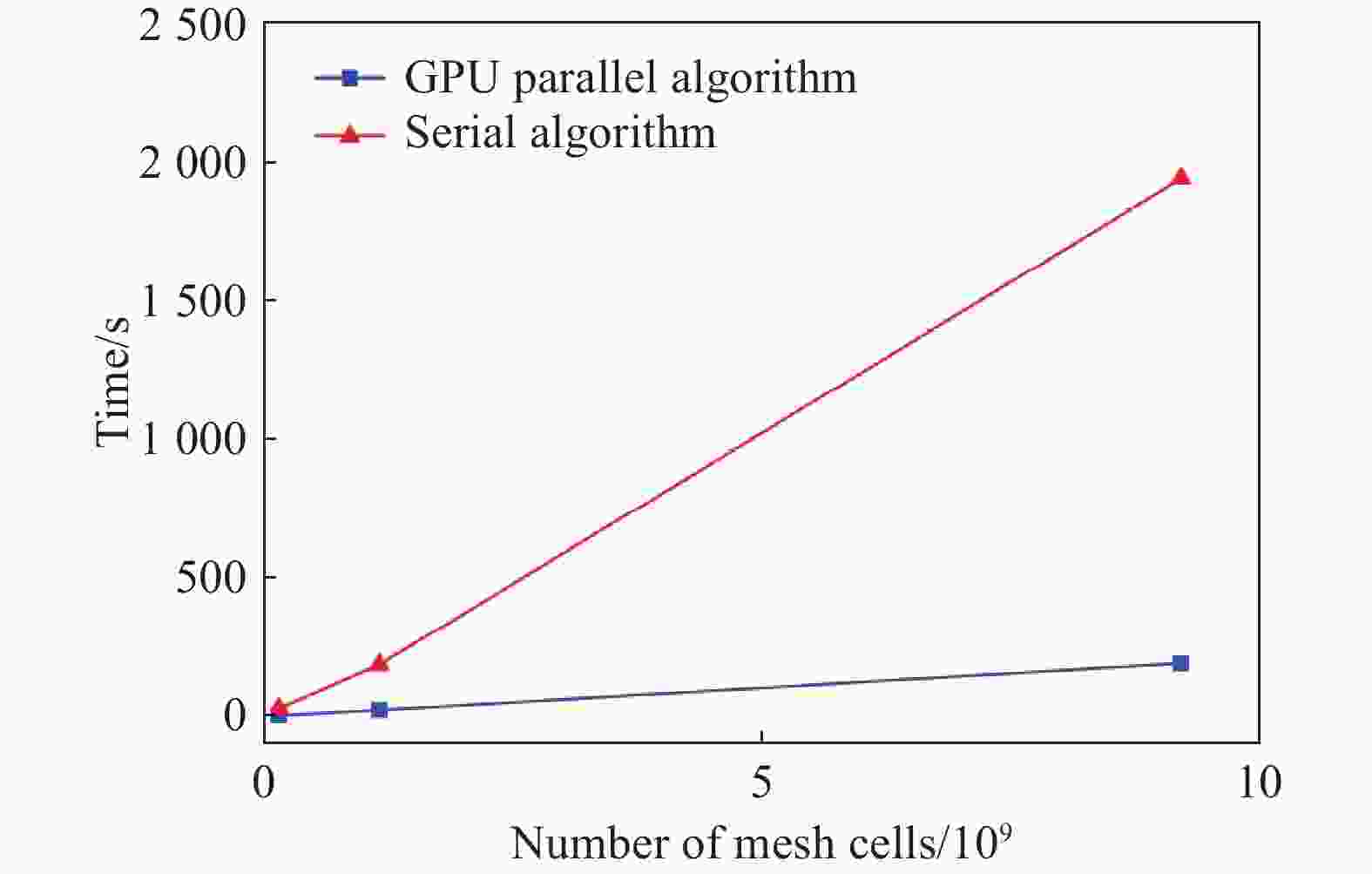
摘要: 三维大规模有限差分网格生成技术是三维有限差分计算的基础，网格生成效率是三维有限差分网格生成的研究热点。传统的阶梯型有限差分网格生成方法主要有射线穿透法和切片法。本文在传统串行射线穿透法的基础上，提出了基于GPU （graphic processing unit）并行计算技术的并行阶梯型有限差分网格生成算法。并行算法应用基于分批次的数据传输策略，使得算法能够处理的数据规模不依赖于GPU内存大小，平衡了数据传输效率和网格生成规模之间的关系。为了减少数据传输量，本文提出的并行算法可以在GPU线程内部相互独立的生成射线起点坐标，进一步提高了并行算法的执行效率和并行化程度。通过数值试验的对比可以看出，并行算法的执行效率远远高于传统射线穿透法。最后，通过有限差分计算实例可以证实并行算法能够满足复杂模型大规模数值模拟的需求。Abstract: Three-dimensional large-scale finite difference mesh generation technology is the basis of three-dimensional finite difference computation, and the efficiency of mesh generation is a research hotspot of three-dimensional finite difference mesh generation. The traditional staircase finite difference mesh generation algorithm mainly includes ray casting algorithm and slicing algorithm. Based on the traditional serial ray casting algorithm, a parallel staircase finite difference mesh generation algorithm based on GPU (graphic processing unit) is proposed in this paper. Parallel algorithm uses batch-based data transmission strategy, which makes the scale of mesh generation independent of GPU memory size, and balances the relationship between data transmission efficiency and mesh generation scale. In order to reduce the time consumption of data transmission between the host memory and the device memory, the parallel algorithm proposed in this paper can generate ray starting coordinates independently within GPU threads, which further improves the execution efficiency and parallelization degree of the parallel algorithm. The comparison of numerical experiments shows that the efficiency of parallel algorithm is much higher than that of traditional ray casting algorithm. Finally, an example of finite difference calculation shows that the parallel algorithm can meet the requirement of large-scale numerical simulation of complex models.
-
图 1 三维计算域，内部几何体和几何体局部图
Figure 1. Three-dimensional computational domain, the geometries in the domain and the details of the geometry
图 2 射线穿透法原理（以XY平面为射线投射平面，Z轴方向为射线方向）
Figure 2. Principle of ray casting method (set the XY plane as the projection plane, and the Z dimension as the ray direction)
图 3 三维几何数据转换与并行计算过程图
Figure 3. Diagram of three-dimensional geometric data conversion and parallel computing process
图 5 桥梁模型及其阶梯型有限差分网格生成结果图及细节放大图
Figure 5. A bridge model, the finite difference mesh generated and the details of the mesh
图 6 本文提出的并行算法与传统算法的网格生成时间比较折线图
Figure 6. Mesh generation time comparison curve between the proposed parallel algorithm and the traditional algorithm
图 8 某厂房三维阶梯型有限差分网格
Figure 8. Three-dimensional finite difference mesh of a factory model
图 10 厂房二层距离楼梯口10 m处关键点的超压变化曲线
Figure 10. Change of overpressure with time at a key point which is 10 m from stairway entrance on the second floor
表 1 不同模型生成相同数量网格单元(1×109)的执行时间
Table 1. Generation times of different models with the cell number of 1×109
模型 面片数量 传统CPU串行算法执行时间/s GPU并行算法执行时间/s 并行加速比 模型 1 19 202 177.54 20.99 8.46 模型 2 78 354 620.23 55.15 11.25 模型 3 95 062 895.83 78.94 11.35 
下载: 导出CSV
-
[1] 马天宝, 任会兰, 李健, 等. 爆炸与冲击问题的大规模高精度计算 [J]. 力学学报, 2016, 48(3): 599–608. DOI: 10.6052/0459-1879-15-382.MA T B, REN H L, LI J, et al. Large scale high precision computation for explosion and impact problems [J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 599–608. DOI: 10.6052/0459-1879-15-382. [2] NING J G, YUAN X P, MA T B, et al. Positivity-preserving moving mesh scheme for two-step reaction model in two dimensions [J]. Computers and Fluids, 2015, 123: 72–86. DOI: 10.1016/j.compfluid.2015.09.011. [3] WANG X, MA T B, NING J G. A pseudo arc-length method for numerical simulation of shock waves [J]. Chinese Physics Letters, 2014, 31(3): 030201. DOI: 10.1088/0256-307X/31/3/030201. [4] 陈龙伟, 张华, 汪旭光. 水中多物质爆炸场的三维数值模拟 [J]. 兵工学报, 2009(S2): 1–4. DOI: 1000-1093(2009) S2-0001-04.CHEN L W, ZHANG H, WANG X G. Three-dimensional numerical simulation of multi-material explosive field in water [J]. Acta Armamentarii, 2009(S2): 1–4. DOI: 1000-1093(2009) S2-0001-04. [5] 张军, 赵宁, 任登凤, 等. Level set方法在自适应Cartesian网格上的应用 [J]. 爆炸与冲击, 2008, 28(5): 438–442. DOI: 10.3321/j.issn:1001-1455.2008.05.009.ZHANG J, ZHAO N, REN D F, et al. Application of the level set method on adaptive Cartesian grids [J]. Explosion and Shock Waves, 2008, 28(5): 438–442. DOI: 10.3321/j.issn:1001-1455.2008.05.009. [6] 肖涵山, 刘刚, 陈作斌, 等. 基于STL文件的笛卡尔网格生成方法研究 [J]. 空气动力学学报, 2006, 24(1): 120–124. DOI: 10.3969/j.issn.0258-1825.2006.01.022.XIAO H S, LIU G, CHEN Z B, et al. The adaptive Cartesian grid generation method based on STL file [J]. Acta Aerodynamica Sinica, 2006, 24(1): 120–124. DOI: 10.3969/j.issn.0258-1825.2006.01.022. [7] PANDEY P M, REDDY N V, DHANDE S G. Slicing procedures in layered manufacturing: a review [J]. Rapid Prototyping Journal, 2003, 9(5): 274–288. DOI: 10.1108/13552540310502185. [8] 赵吉宾, 刘伟军. 快速成型技术中分层算法的研究与进展 [J]. 计算机集成制造系统, 2009, 15(2): 209–221.ZHAO J B, LIU W J. Recent progress in slicing algorithm of rapid prototyping technology [J]. Computer Integrated Manufacturing Systems, 2009, 15(2): 209–221. [9] FEI G L, MA T B, HAO L. Large-scale high performance computation on 3D explosion and shock problems [J]. Applied Mathematics and Mechanics, 2011, 32(3): 375–382. DOI: 10.1007/s10483-011-1422-7. [10] MACGILLIVRAY J T. Trillion cell CAD-based Cartesian mesh generator for the finite-difference time-domain method on a single-processor 4-GB workstation [J]. IEEE Transactions on Antennas and Propagation, 2008, 56(8): 2187–2190. DOI: 10.1109/TAP.2008.926790. [11] BERENS M K, FLINTOFT I D, DAWSON J F. Structured Mesh Generation: open-source automatic nonuniform mesh generation for FDTD simulation [J]. IEEE Antennas and Propagation Magazine, 2016, 58(3): 45–55. DOI: 10.1109/MAP.2016.2541606. [12] NING J G, MA T B, LIN G H. A mesh generator for 3-D explosion simulations using the staircase boundary approach in Cartesian coordinates based on STL models [J]. Advances in Engineering Software, 2014, 67(1): 148–155. DOI: 10.1016/j.advengsoft.2013.09.007. [13] ISHIDA T, TAKAHASHI S, NAKAHASHI K. Efficient and robust Cartesian mesh generation for building-cube method [J]. Journal of Computational Science and Technology, 2008, 2(4): 435–446. DOI: 10.1299/jcst.2.435. [14] FOTEINOS P, CHRISOCHOIDES N. High quality real-time image-to-mesh conversion for finite element simulations [J]. Journal of Parallel and Distributed Computing, 2013, 74(2): 2123–2140. DOI: 10.1109/SC.Companion.2012.322. [15] QI M, CAO T T, TAN T S. Computing 2D constrained Delaunay triangulation using the GPU [J]. IEEE Transactions on Visualization and Computer Graphics, 2013, 19(5): 736–748. DOI: 10.1109/TVCG.2012.307. [16] PARK S, SHIN H. Efficient generation of adaptive Cartesian mesh for computational fluid dynamics using GPU [J]. International Journal for Numerical Methods in Fluids, 2012, 70(11): 1393–1404. DOI: 10.1002/fld.2750. [17] SCHWARZ M, SEIDEL H P. Fast parallel surface and solid voxelization on GPUs [J]. ACM Transactions on Graphics, 2010, 29(6): 1–10. DOI: 10.1145/1882261.1866201. [18] SZILVI-NAGY M, MATYASI G. Analysis of STL files [J]. Mathematical and Computer Modelling, 2003, 38(7): 945–960. DOI: 10.1016/s0895-7177(03)90079-3. [19] POSPICHAL P, JAROS J, SCHWARZ J. Parallel genetic algorithm on the CUDA architecture [J]. Lecture Notes in Computer Science, 2010, 6024: 442–451. DOI: 10.1007/978-3-642-12239-2_46. [20] NING J G, MA T B, FEI G L. Multi-material Eulerian method and parallel computation for 3D explosion and impact problems [J]. International Journal of Computational Methods, 2014, 11(5): 1350079. DOI: 10.1142/S0219876213500795. -
点击查看大图
计量
- 文章访问数: 8035
- HTML全文浏览量: 1753
- PDF下载量: 79
- 被引次数: 0