Experimental study of LPG storage tank BLEVE in unconfined space under fire
-
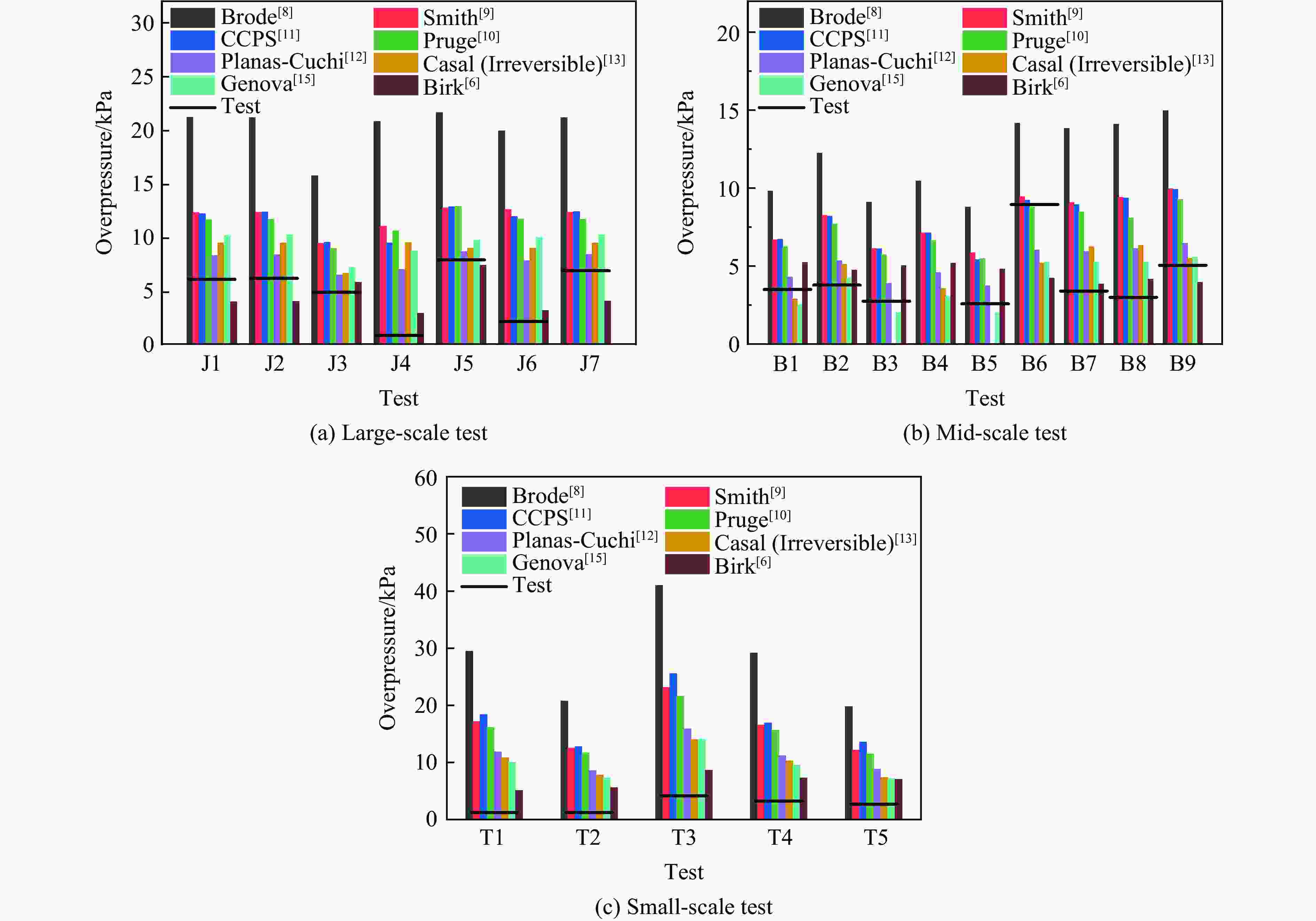
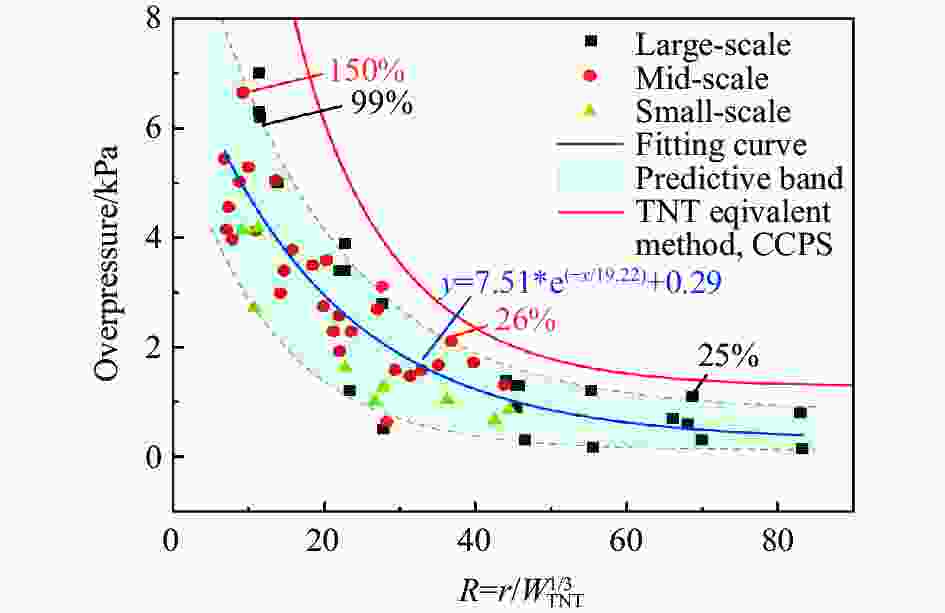
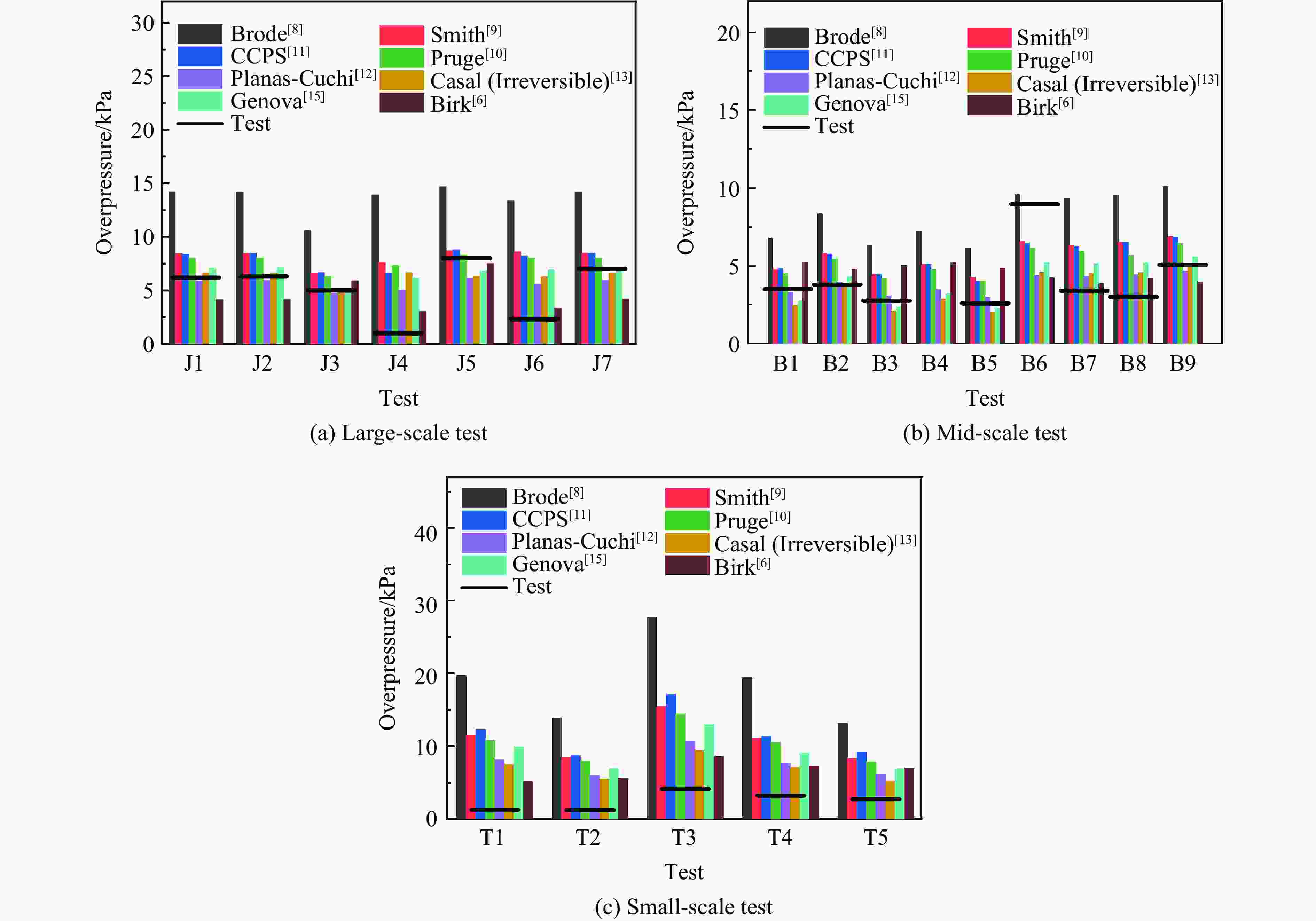
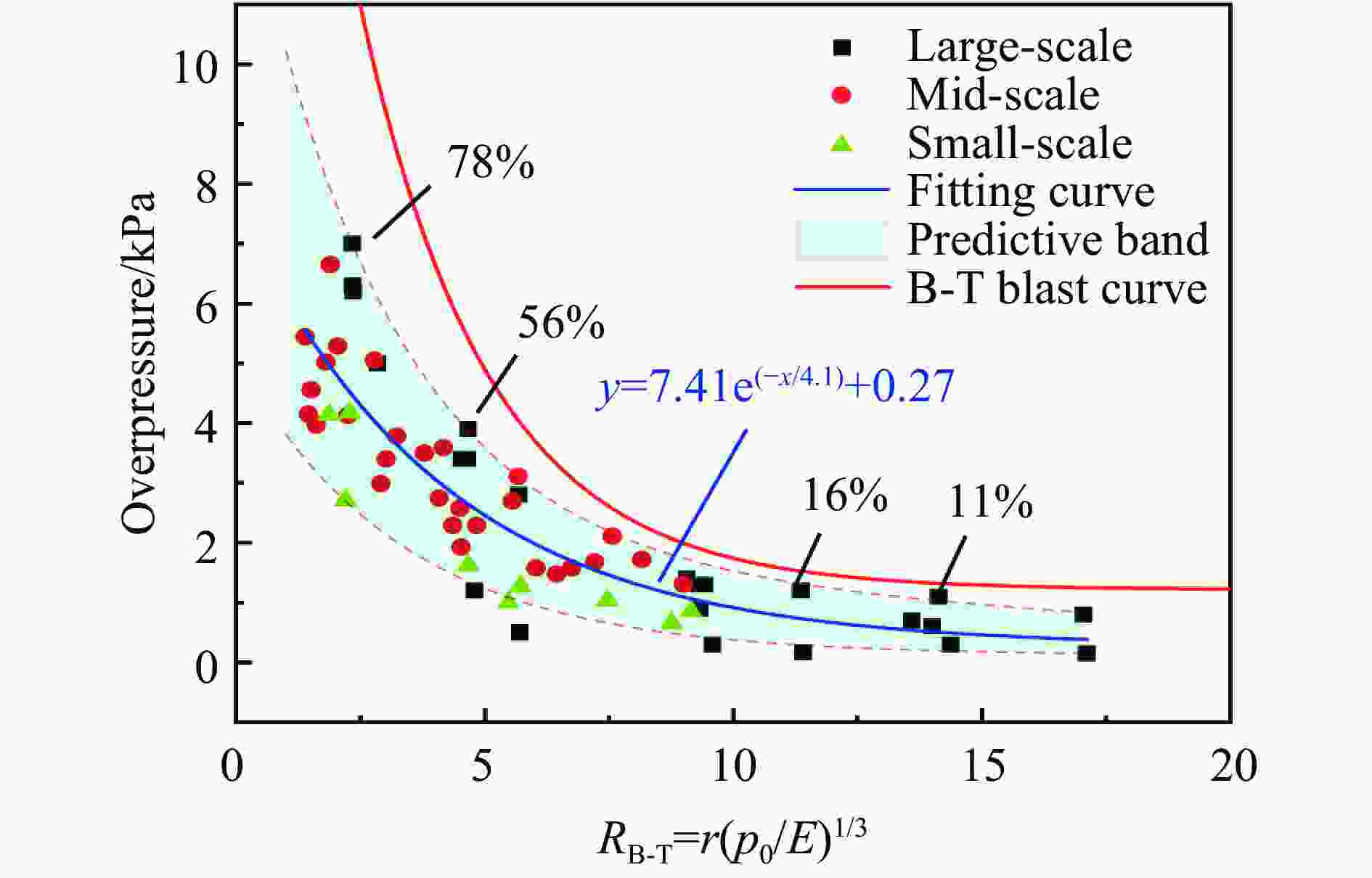
摘要: 为研究火灾条件下开敞空间液化石油气（liquefied petroleum gas, LPG）储罐沸腾液体膨胀蒸汽爆炸（boiling liquid expansion vapor explosion，BLEVE）的荷载特征及爆炸波传播规律，研制了带滤波片的储罐爆炸试验装置，开展了小尺寸LPG储罐BLEVE试验，分析了LPG储罐的BLEVE过程及超压荷载特征，讨论了滤波片、LPG质量、储罐形状等因素对爆炸超压的影响，总结了已有BLEVE超压荷载的简化计算模型，对比试验数据与简化模型预测结果，给出了简化计算模型的适用范围。研究结果表明：次生蒸气云爆炸对开敞空间BLEVE超压荷载影响有限；BLEVE超压荷载峰值随爆源中心距离的增加而减小，随储存介质质量的增大而增大；在BLEVE超压荷载简化计算模型中，使用Brode模型计算爆炸能量最为保守，Planas模型仅能较准确地预测大尺度试验的结果，Birk模型则能较准确地预测大、中、小尺度试验的结果，但其结果略低于实验结果；规范建议的超压荷载计算方法中，Baker-Tang爆炸曲线法预测效果优于TNT当量法。Abstract: Ten batches of liquefied petroleum gas (LPG) tank explosion tests under fires were conducted to investigate the overpressure load characteristics and blast wave propagation of LPG tank boiling liquid expansion vapor explosion (BLEVE) in unconfined space. Five different LPG tanks were considered in the tests with the variations of filters, LPG mass and tank shape. The explosion process and overpressure load of BLEVE were recorded by high-speed camera and overpressure sensors. The effects of filters, LPG mass, tank shape on the overpressure loads of BLEVEs were revealed and discussed. The empirical models of BLEVE overpressure loads are reviewed and the predictions of the simplified models are compared with the data of multi-scale BLEVE tests. The limitation and suggestion of the simplified empirical models are proposed. It is found that the existence of filters during explosion tests brings about the secondary gas cloud explosion of LPG tank BLEVE and the effect of secondary vapor cloud explosion on overpressure loads of BLEVE in unconfined space is limited due to the specific testing conditions. Typically, the overpressure loads of BLEVE have two positive phases and one negative phase, which is significantly different from the loads of TNT and gas explosions. The peak value of BLEVE overpressure loads decreases with the increase of distance and the decrease of LPG mass. Among the existed empirical models, the Brode model is the most conservative in predicting the BLEVE overpressure loads and the Planas model can predict the large scale BLEVE reasonably. The Birk model shows good predictions for large, medium and small scale tests, while the results are prone to danger. With the increase of scaled distance, the peak value of BLEVE overpressure loads decays exponentially. Moreover, the performance of the Baker-Tang blast curve method is better than that of the TNT equivalent method in the prediction of BLEVE loads.
-
Key words:
- LPG /
- BLEVE /
- overpressure load /
- simplified empirical model /
- muti-scale
-
图 6 LPG储罐爆炸超压时程曲线对比（有/无火球）
Figure 6. Overpressure-time history profiles with and without fireball
图 7 典型工况下LPG储罐爆炸的超压时程曲线
Figure 7. Overpressure-time history profiles of typical LPG tank explosion
图 12 BLEVE超压分布（TNT当量法）
Figure 12. BLEVE overpressure distribution (TNT equivalent method)
图 14 BLEVE超压分布（Baker-Tang爆炸曲线法）
Figure 14. BLEVE overpressure distribution (Baker-Tang blast curve method)
表 1 试验工况
Table 1. Test conditions
工况 滤波片 储罐质量/g 储罐体积/cm3 储罐长径比（L/D） 储罐形状 T1 有 230 660 3.00 长罐 T2 有 110 430 2.00 长罐 T3 有 450 1380 1.32 扁罐 T4 有 230 855 0.82 扁罐 T5 有 110 445 0.78 扁罐 T6 无 230 660 3.00 长罐 T7 无 110 430 2.00 长罐 T8 无 450 1380 1.32 扁罐 T9 无 230 855 0.82 扁罐 T10 无 110 445 0.78 扁罐 
下载: 导出CSV
表 2 测试结果
Table 2. Testing results
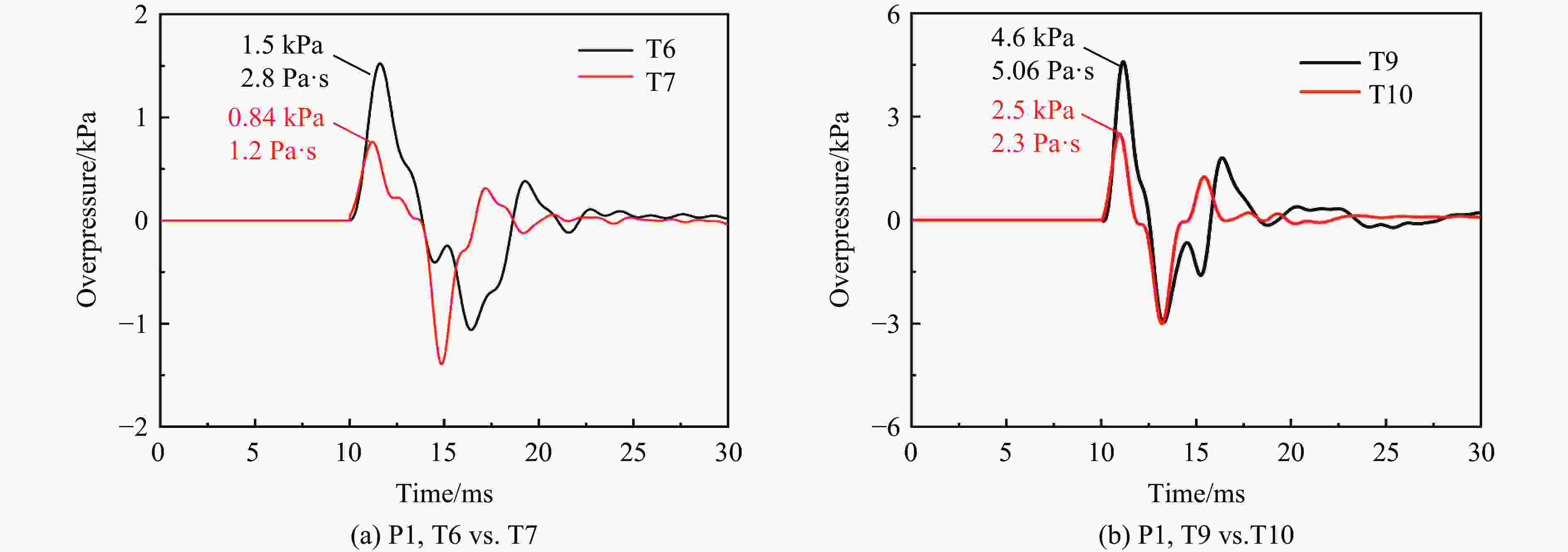
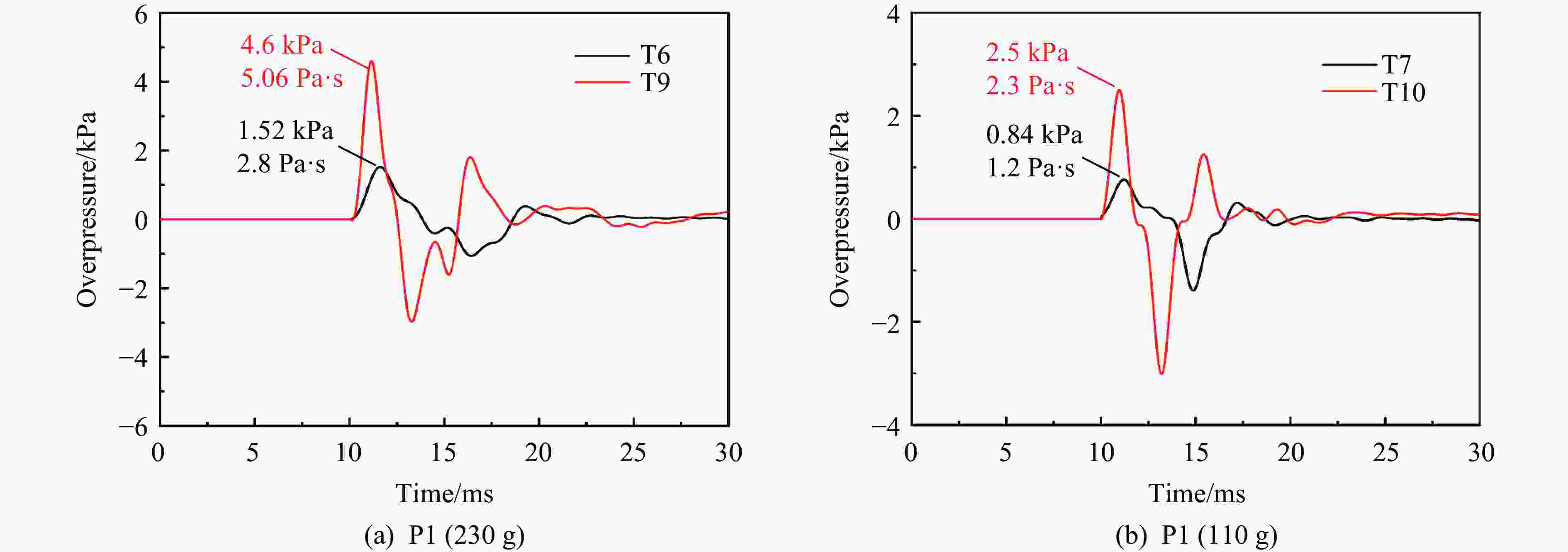
工况 储罐 是否产生火球 极限压力/MPa 压力峰值/kPa P1 P2 P3 P4 P5 P6 T1 L230g 是 1.88 1.26 0.61 0.33 0.36 0.30 0.26 T2 L110g 是 1.70 1.22 0.86 0.31 0.36 0.34 0.25 T3 F450g 是 2.02 4.18 1.63 1.04 1.27 1.14 0.75 T4 F230g 是 1.61 4.18 1.63 1.12 1.41 1.23 0.92 T5 F110g 是 2.17 2.71 1.00 0.66 0.75 0.66 0.54 T6 L230g 否 1.88 1.52 0.42 0.37 0.52 0.37 0.32 T7 L110g 否 1.70 0.84 0.30 0.28 0.28 0.23 0.14 T8 F450g 否 2.02 4.10 1.83 1.14 1.32 1.27 0.70 T9 F230g 否 1.61 4.60 1.60 1.07 1.36 1.25 0.76 T10 F110g 否 2.17 2.50 0.94 0.66 0.80 0.73 0.52
下载: 导出CSV
表 3 液相与气相能量对比
Table 3. Comparison of liquid and vapor energies
储罐 储罐体积/cm3 气体填充率/% mL/g mV/g EL/kJ EV/kJ E/kJ L230g 660 83 222 8 65.40 1.19 66.60 L110g 430 58 101 9 28.08 1.28 29.36 F450g 1380 69 428 22 131.41 3.36 134.77 F230g 855 54 214 16 57.65 2.22 59.87 F110g 445 50 97 13 31.03 2.04 33.17 注: (1)液体和气体能量计算公式：E=m(u1-u2)。(2)$m$为液体或气体质量，$ {m_{\text{L}}} $为液体质量，${m_{\text{V}}}$为气体质量，${E_{\text{L}}}$为液相爆炸能量，${E_{\text{V}}}$为气相爆炸总能量，$E$为爆炸总能量，$ {u_{\text{1}}} $为爆炸前总内能，${u_{\text{2}}}$为爆炸后总内能。
下载: 导出CSV
表 4 能量计算公式
Table 4. Energy calculation method
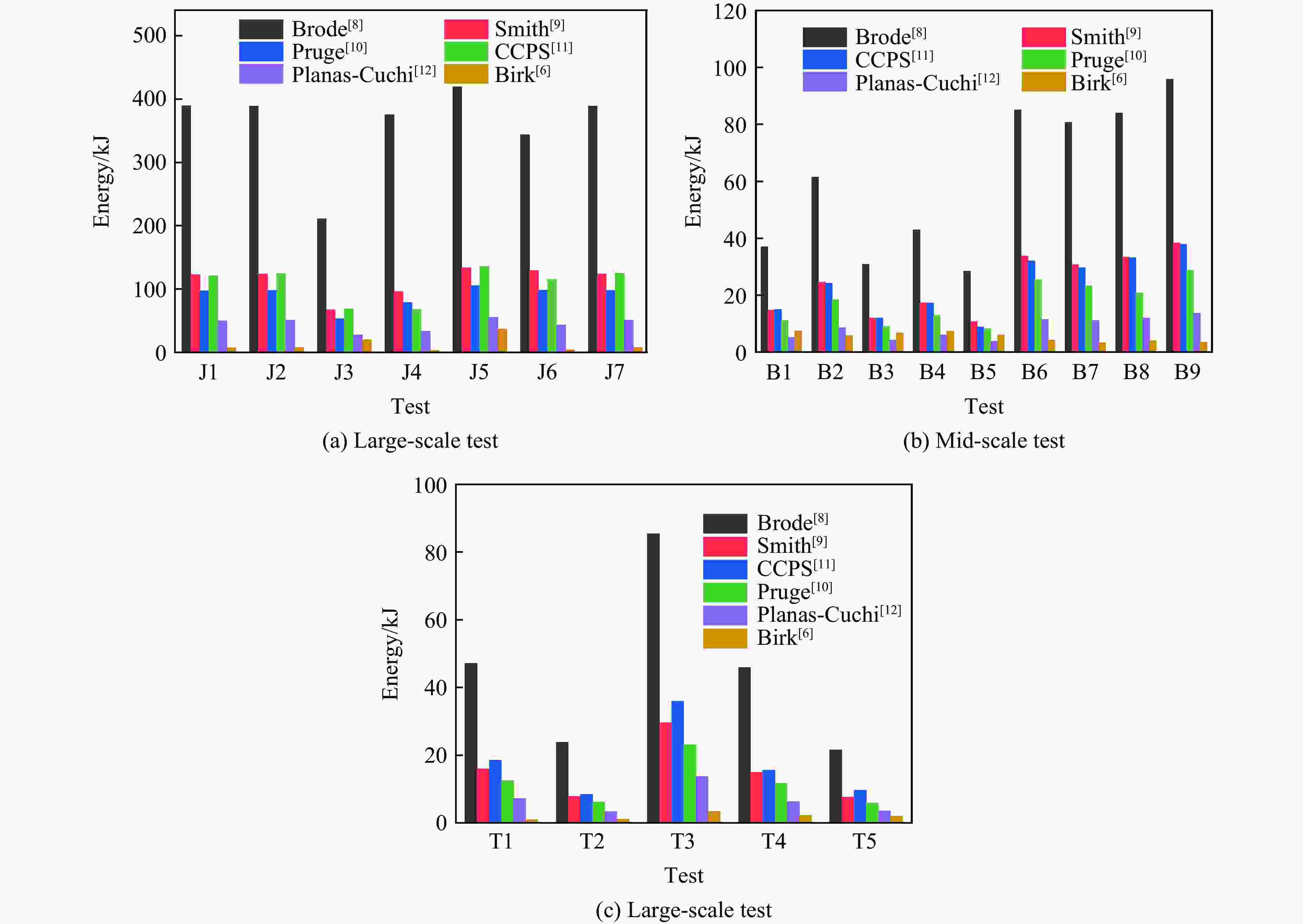
来源 能量来源 简化过程 气体行为 折减系数β 能量计算公式 Brode[8] 气相 恒容过程 理想气体 0.4 $ E = pV\ln \left( {\dfrac{p}{{{p_0}}}} \right) $ Smith[9] 气相 等温过程 理想气体 0.4 $ E = pV\ln \left( {\dfrac{p}{{{p_0}}}} \right) $ Prugh[10] 气相 等熵膨胀 理想气体 0.4 $E = \dfrac{{pV}}{{\gamma - 1}}\left[ {1 - {{\left( {\dfrac{{{p_0}}}{p}} \right)}^{^{(\gamma - 1)/\gamma }}}} \right]$ CCPS[11] 液相+气相 等熵膨胀 真实气体 0.4 $ E = {m_{{\text{L0}}}}{u_{{\text{L0}}}} + {m_{{\text{V0}}}}{u_{{\text{V0}}}} - {m_{\text{L}}}{u_{\text{L}}} - {m_{\text{V}}}{u_{\text{V}}} $ Planas-Cuchi[12] 液相+气相 绝热不可逆过程 真实气体 0.4 $ E = {m_{\text{T}}}{u_{{\text{L0}}}} - \left( {{u_{{\text{L0}}}} - {u_{{\text{V0}}}}} \right){m_{\text{T}}}x - U $ Casal[13] 液相 等熵膨胀和绝热不可逆过程 真实气体 0.05/0.14 $E = \beta {m_{\text{L}}}\left( {{h_{\text{L}}} - {h_{{\text{L0}}}}} \right)$ Genova[15] 液相 等熵膨胀 真实气体 0.07 $ E = \beta {m_{\text{L}}}{c_{{p}}}\Delta T $ Birk[6] 气相 等熵膨胀 真实气体 1 $E = {m_{\text{V}}}\left( {{u_{\text{1}}} - {u_{\text{2}}}} \right)$
下载: 导出CSV
-
[1] 侯淑雅, 王智, 栾笑阳, 等. 浙江温岭槽罐车爆炸事故分析 [J]. 南京工业大学学报(自然科学版), 2021, 43(2): 144–149. DOI: 10.3969/j.issn.1671-7627.2021.02.002.HOU S Y, WANG Z, LUAN X Y, et al. Analysis of tank truck explosion accident in Wenling, Zhejiang Province [J]. Journal of Nanjing University of Technology (Natural Science Edition), 2021, 43(2): 144–149. DOI: 10.3969/j.issn.1671-7627.2021.02.002. [2] LABOUREUR D, HEYMES F, LAPEBIE E, et al. BLEVE overpressure: multiscale comparison of blast wave modeling [J]. Process Safety Progress,, 2015, 33(3): 274–284. DOI: 10.1002/prs.11626. [3] STAWCZYK J. Experimental evaluation of LPG tank explosion hazards [J]. Journal of Hazardous Materials, 2003, 96(2/3): 189–200. DOI: 10.1016/S0304-3894(02)00198-X. [4] BIRK A M, POIRIER D, DAVISON C. On the response of 500gal propane tanks to a 25% engulfing fire [J]. Journal of Loss Prevention in the Process Industries, 2006, 19(6): 527–541. DOI: 10.1016/j.jlp.2005.12.008. [5] BIRK A M, VANDERSTEEN J D J. On the transition from non-BLEVE to BLEVE failure for a 1.8 m3 propane tank [J]. Journal of Pressure Vessel Technology, 2006, 128(4): 648–655. DOI: 10.1115/1.2349579. [6] BIRK A M, DAVISON C, CUNNINGHAM M. Blast overpressures from medium scale BLEVE tests [J]. Journal of Loss Prevention in the Process Industries, 2007, 20(3): 194–206. DOI: 10.1016/j.jlp.2007.03.001. [7] 胡昆, 陈国华, 周志航, 等. 爆炸冲击波作用下化工设备易损性研究评述 [J]. 化工进展, 2019, 38(4): 1634–1645. DOI: 10.16085/j.issn.1000-6613.2018-0756.HU K, CHEN G H, ZHOU Z H, et al. Review of the vulnerabilityofchemical equipment subjected to blastwave [J]. Chemical Industry and Engineering Progress, 2019, 38(4): 1634–1645. DOI: 10.16085/j.issn.1000-6613.2018-0756. [8] BRODE H L. Blast wave from a spherical charge [J]. Physics of Fluids, 1959, 2(2): 217–229. DOI: 10.1063/1.1705911. [9] SMITH J M. Introduction to chemical engineering thermodynamics [M]. 5th ed. New York: McGraw-Hill, 1996. [10] PRUGH R W. Quantitative evaluation of “BLEVE” hazards [J]. Journal of Fire Protection Engineering, 1991, 3(1): 9–24. DOI: 10.1177/104239159100300102. [11] SAFETY C F C P . Guidelines for vapor cloud explosion, pressure vessel burst, BLEVE, and flash fire hazards [M]. 2nd ed. Hoboken: John Wiley & Sons, Inc. , 2010. [12] PLANAS-CUCHI E, SALLA J M, CASAL J. Calculating overpressure from BLEVE explosions [J]. Journal of Loss Prevention in the Process Industries, 2004, 17(6): 431–436. DOI: 10.1016/j.jlp.2004.08.002. [13] CASAL J, SALLA J M. Using liquid superheating energy for a quick estimation of overpressure in BLEVEs and similar explosions [J]. Journal of Hazardous Materials, 2006, 137(3): 1321–1327. DOI: 10.1016/j.jhazmat.2006.05.001. [14] SALLA J M, DEMICHELA M, CASAL J. BLEVE: a new approach to the superheat limit temperature [J]. Journal of Loss Prevention in the Process Industries, 2006, 19(6): 690–700. DOI: 10.1016/j.jlp.2006.04.004. [15] GENOVA B, SILVESTRINI M, TRUJILLO F J L. Evaluation of the blast-wave overpressure and fragments initial velocity for a BLEVE event via empirical correlations derived by a simplified model of released energy [J]. Journal of Loss Prevention in the Process Industries, 2008, 21(1): 110–117. DOI: 10.1016/j.jlp.2007.11.004. [16] 孔维轩, 刘宁, 林煦淏等. 国内通用水压试验标准内容对比分析 [J]. 环境技术, 2023, 41(7): 153–158. DOI: 10.3969/j.issn.1004-7204.2023.07.030.KONG W X, LIU N, LIN X H, et al. Comparative analysis of domestic general hydraulic test standards [J]. Environmental Technology, 2023, 41(7): 153–158. DOI: 10.3969/j.issn.1004-7204.2023.07.030. [17] KINNEY G F, GRAHAM K J. Explosives shocks in air [M]. 2nd ed. Berlin: Springer, 1985. [18] BAKER W E, COX P A, WESTINE P S, et al. Explosion hazards and evaluation [M]. Amsterdam: Elsevier, 2012. [19] HEMMATIAN B, PLANAS E, CASAL J. Comparative analysis of BLEVE mechanical energy and overpressure modelling [J]. Process Safety and Environmental Protection, 2017, 106: 138–149. DOI: 10.1016/j.psep.2017.01.007. [20] BUBBICO R, MARCHINI M. Assessment of an explosive LPG release accident: a case study [J]. Journal of Hazardous Materials, 2008, 155(3): 558–565. DOI: 10.1016/j.jhazmat.2007.11.097. -
图(14) / 表(4)
计量
- 文章访问数: 177
- HTML全文浏览量: 61
- PDF下载量: 97
- 被引次数: 0