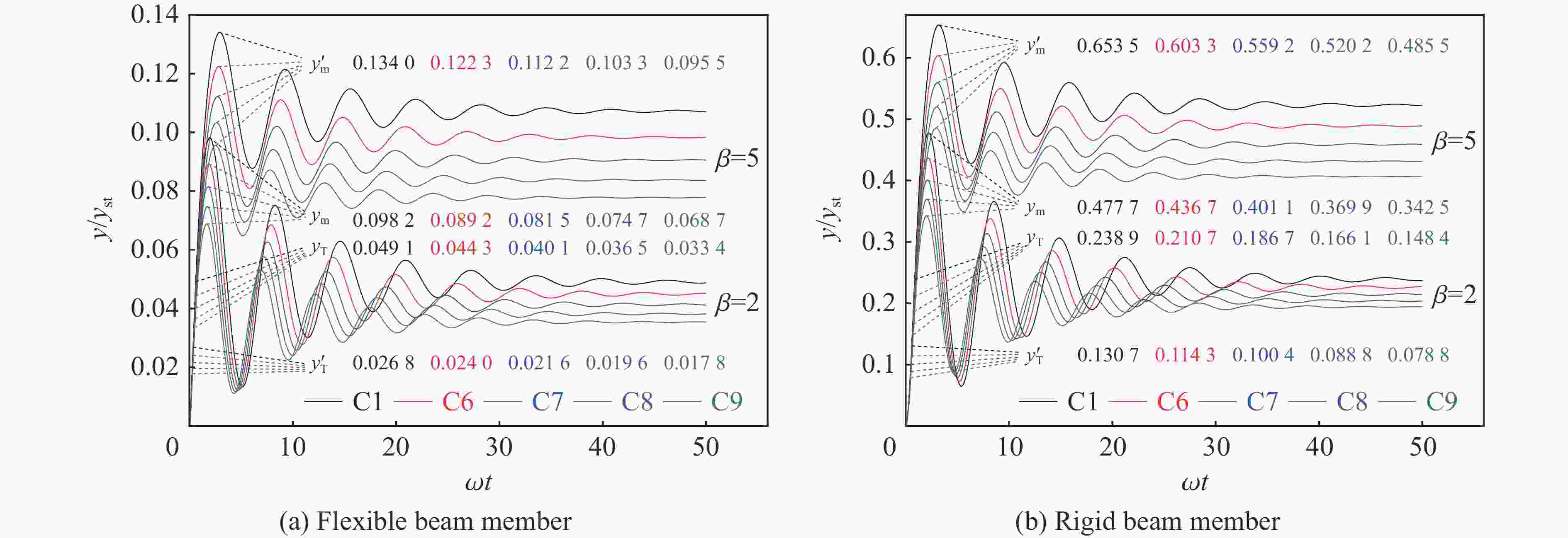
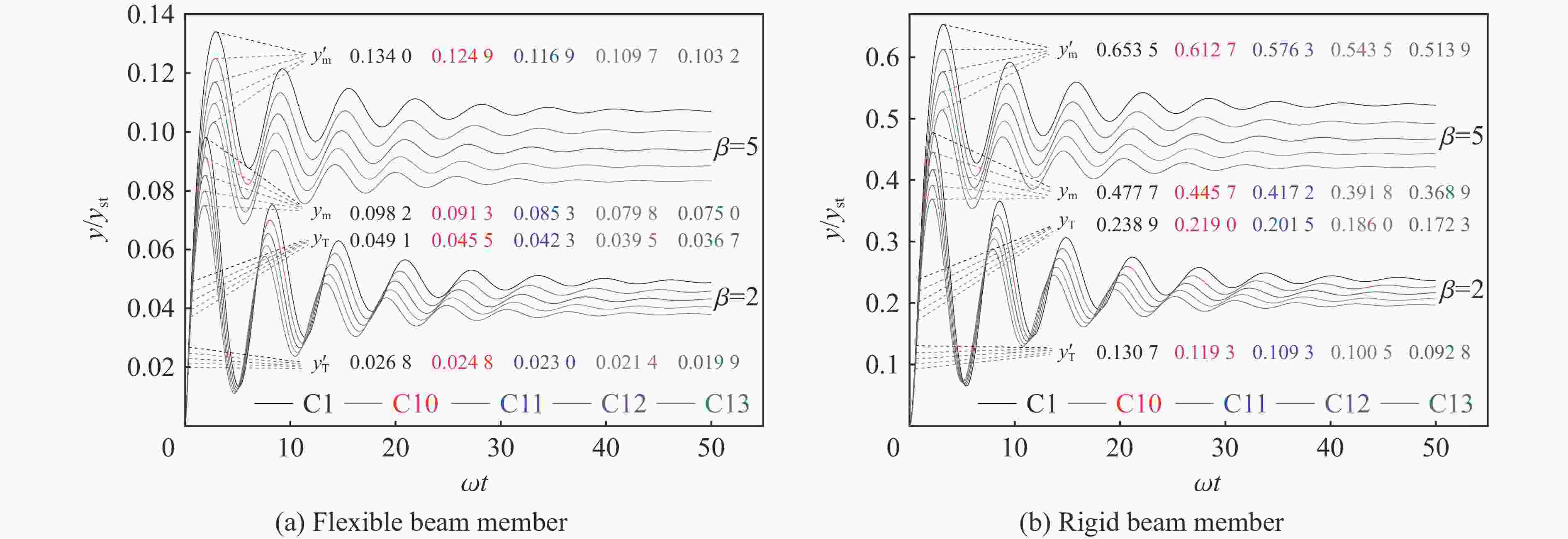
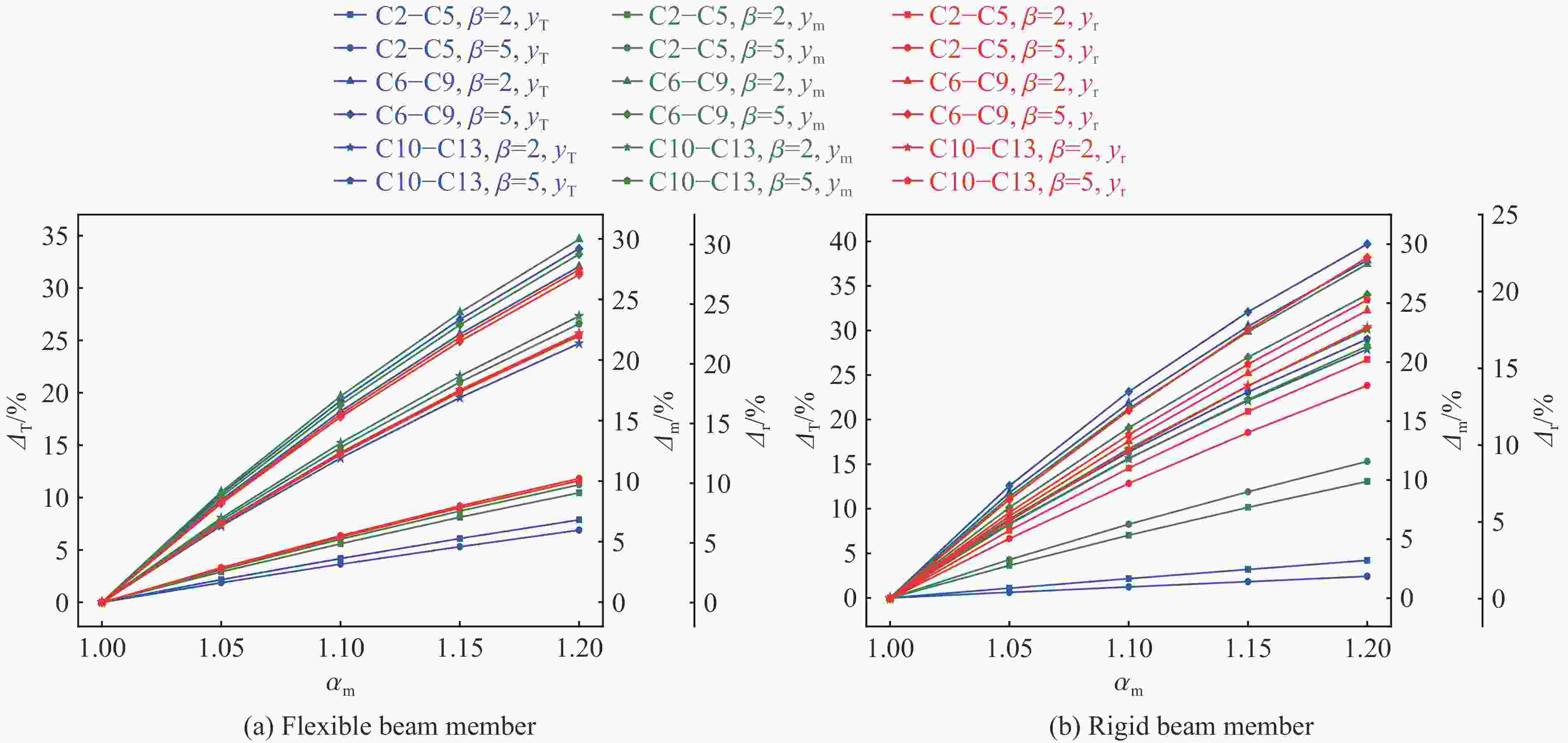
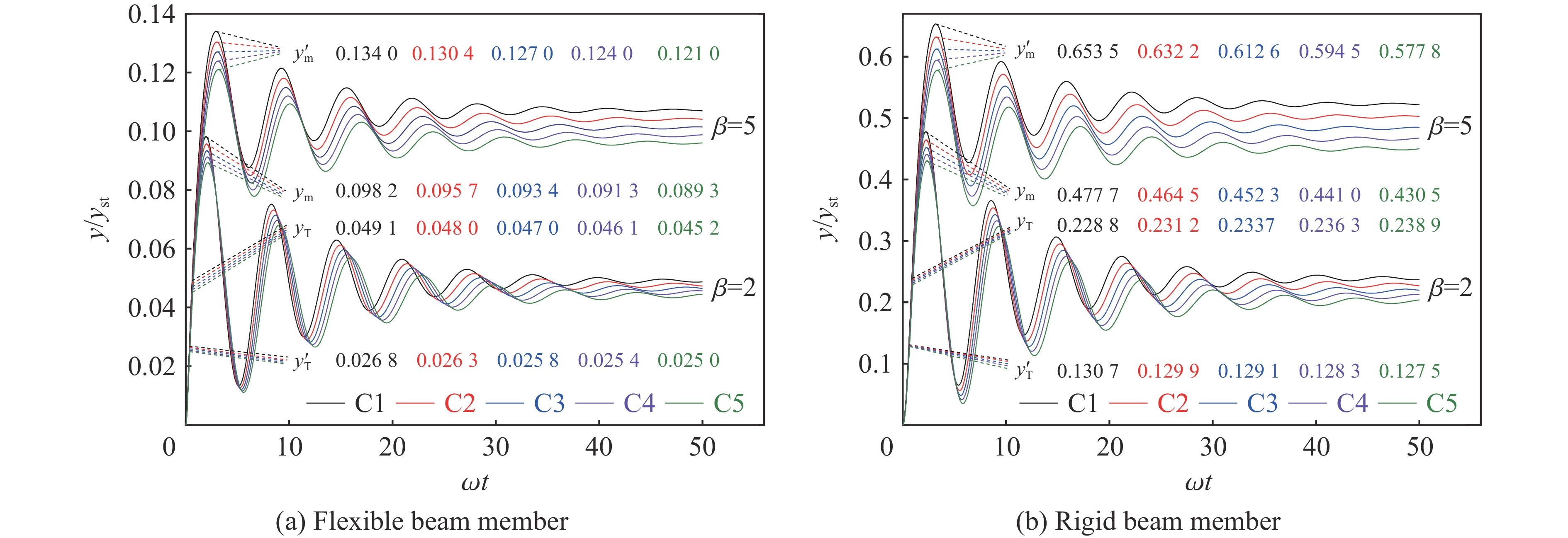
Effect of mass parameter on vibration displacement of beam member under air blast loading
-
摘要: 为研究质量参数对空爆荷载梁构件振动位移的影响,以等效单自由度法为基本方法,理论推导了柔性及刚性2类梁构件含质量参数在弹性、塑性各阶段的振动位移解,选择矩形截面、圆截面为梁构件典型截面,设计并计算了质量参数在1.00~1.20范围内的13种典型工况。结果表明:对于空爆荷载柔性及刚性2类梁构件,增大其截面面积后,仅考虑质量参数计算振动位移时误差较大,应按质量参数及产生的附加刚度参数耦合效应分析;对于矩形截面梁构件,采用质量参数与刚度参数耦合计算时,其最大弹性位移、最大弹塑性位移和残余变形降低幅度分别约为仅采用质量参数计算结果的4.75、3.28和2.96倍;对于圆截面梁构件,则分别为3.57、2.56和2.32倍;该结论在柔性梁构件及刚性梁构件均适用且无明显差异。Abstract: By exploring the effect of mass parameter on the vibration displacement of beam members under air blast loading, an effective method was proposed to reduce the vibration displacement of beam members by increasing mass. An equivalent single degree of freedom (SDOF) system was used to analyze vibration displacement for beam members. The displacement formulas with mass parameter for flexible and rigid beam members in each stage under air blast loading were respectively established. These stages included elastic forced vibration, elastic free vibration, plastic forced vibration, plastic free vibration, and rebound vibration. Rectangular and circular sections were selected as typical cross sections of beam members, and 13 typical calculation cases with mass parameters ranging from 1.00 to 1.20 were designed. The vibration displacement-time history curves, maximum elastic displacement, maximum elastic-plastic displacement, and residual deformation were calculated and analyzed. Taking the data with a mass parameter value of 1.0 as the reference value, the displacement reduction rate of other calculation cases relative to the reference value could be obtained. The difference between the types of beam members for displacement reduction rate was further analyzed. The results are as follows. For flexible and rigid beam members subjected to air blast loading, increasing the cross-sectional area and considering only the mass parameter will result in a smaller reduction in vibration displacement. Therefore, the displacement should be analyzed according to the coupling effect of the mass parameter and additional stiffness parameter. For beam members with rectangular cross-sections, the reduction ranges of maximum elastic displacement, maximum elastic-plastic displacement, and residual deformation calculated from the coupled effect of mass parameter and stiffness parameter are about 4.75, 3.28, and 2.96 times that of mass parameter alone. For beams with circular cross-section, the data are 3.75, 2.56, and 2.32 times. These conclusions apply to both flexible beam members and rigid beam members, and there is no significant difference.
-
Key words:
- air blast loading /
- mass parameter /
- beam member /
- dynamic response /
- stiffness /
- residual deformation
-
表 1 质量参数典型工况
Table 1. Typical calculation cases for mass parameter
工况(矩形、圆) αm αk 工况(矩形) αm αk 工况(圆) αm αk C1 1.00 1.00 C6 1.05 1.16 C10 1.05 1.10 C2 1.05 1.00 C7 1.10 1.33 C11 1.10 1.21 C3 1.10 1.00 C8 1.15 1.52 C12 1.15 1.32 C4 1.15 1.00 C9 1.20 1.73 C13 1.20 1.44 C5 1.20 1.00 表 2
$\beta=2 $ 时位移降低率以及两类梁构件差异性结果Table 2. Displacement reduction ratios and difference between flexible beam members with
$\beta=2 $ and rigid beam members工况 柔性梁构件 刚性梁构件 Δ2T/% Δ2m/% Δ2r/% ΔT/% Δm/% Δr/% ΔT/% Δm/% Δr/% C2 2.16 2.51 2.85 1.09 2.77 4.45 1.07 −0.26 −1.60 C3 4.18 4.84 5.49 2.15 5.32 8.49 2.03 −0.48 −3.00 C4 6.08 7.01 7.93 3.19 7.69 12.18 2.89 −0.68 −4.25 C5 7.87 9.04 10.20 4.21 9.89 15.56 3.66 −0.85 −5.36 C6 9.78 9.11 8.44 11.80 8.59 5.38 −2.02 0.52 3.06 C7 18.24 17.01 15.78 21.85 16.05 10.24 −3.61 0.96 5.54 C8 25.60 23.91 22.22 30.46 22.57 14.68 −4.86 1.34 7.54 C9 32.04 29.97 27.89 37.87 28.32 18.76 −5.83 1.65 9.13 C10 7.30 6.96 6.62 8.33 6.70 5.07 −1.03 0.26 1.55 C11 13.77 13.15 12.52 15.66 12.66 9.66 −1.89 0.48 2.86 C12 19.54 18.67 17.80 22.13 17.99 13.85 −2.59 0.68 3.95 C13 24.70 23.62 22.55 27.88 22.78 17.68 −3.18 0.84 4.87 表 3
$\beta=5 $ 时位移降低率以及两类梁构件差异性结果Table 3. Displacement reduction ratios and difference between flexible beam members with
$\beta=5 $ and rigid beam members工况 柔性梁构件 刚性梁构件 Δ5T/% Δ5m/% Δ5r/% ΔT/% Δm/% Δr/% ΔT/% Δm/% Δr/% C2 1.87 2.71 2.91 0.62 3.25 3.91 1.25 −0.54 −1.00 C3 3.64 5.21 5.60 1.23 6.25 7.50 2.41 −1.04 −1.90 C4 5.31 7.53 8.09 1.83 9.02 10.82 3.48 −1.49 −2.73 C5 6.89 9.70 10.40 2.41 11.58 13.88 4.48 −1.88 −3.48 C6 10.34 8.72 8.31 12.58 7.68 6.46 −2.24 1.04 1.85 C7 19.25 16.29 15.55 23.14 14.43 12.25 −3.89 1.86 3.30 C8 26.99 22.91 21.89 32.08 20.40 17.48 −5.09 2.51 4.41 C9 33.75 28.73 27.47 39.69 25.71 22.21 −5.94 3.02 5.26 C10 7.58 6.77 6.56 8.75 6.24 5.61 −1.17 0.53 0.95 C11 14.29 12.78 12.40 16.38 11.82 10.67 −2.09 0.96 1.73 C12 20.26 18.16 17.63 23.10 16.83 15.26 −2.84 1.33 2.37 C13 25.60 22.99 22.34 29.03 21.36 19.44 −3.43 1.63 2.90 -
[1] 中华人民共和国建设部, 中华人民共和国国家质量监督检验检疫总局. 人民防空地下室设计规范: GB 50038—2005 [S]. 北京: 中国计划出版社, 2006.Ministry of Construction of the PRC, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Code for design of civil air defence basement: GB 50038—2005 [S]. Beijing: China Planning Press, 2006. [2] Department of the Army, the Navy and the Air Force. The design of structures to resist the effects of accidental explosions: TM5-1300 [S]. Washington: US Department of the Army, the Navy, and the Air Force, 1990. [3] Canadian Standards Association. Design and assessment of buildings subjected to blast loads: CSA/S 850-12 [S]. Mississauga: CSA, 2012. [4] 中华人民共和国住房和城乡建设部. 建筑结构荷载规范: GB 50009—2012 [S]. 北京: 中国建筑工业出版社, 2012.Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Load code for the design of building structures: GB 50009—2012 [S]. Beijing: China Architecture & Building Press, 2012. [5] BIGGS J M. Introduction to structural dynamics [M]. New York: McGraw-Hill, 1964: 315–327. [6] YAO S J, ZHANG D, CHEN X G, et al. Experimental and numerical study on the dynamic response of RC slabs under blast loading [J]. Engineering Failure Analysis, 2016, 66: 120–129. DOI: 10.1016/j.engfailanal.2016.04.027. [7] YAN J B, LIU Y, BAI F, et al. Dynamic response of GFRP-reinforced UHPC beams under close-in blast loading [J]. Materials and Design, 2022, 223: 111140. DOI: 10.1016/J.MATDES.2022.111140. [8] LIAO Z, LI Z Z, XUE Y L, et al. Study on anti-explosion behavior of high-strength reinforced concrete beam under blast loading [J]. Strength of Materials, 2019, 51(6): 926–938. DOI: 10.1007/s11223-020-00143-4. [9] LI Y, AOUDE H. Blast response of beams built with high-strength concrete and high-strength ASTM A1035 bars [J]. International Journal of Impact Engineering, 2019, 130: 41–67. DOI: 10.1016/j.ijimpeng.2019.02.007. [10] LI Y, ALGASSEM O, AOUDE H. Response of high-strength reinforced concrete beams under shock-tube induced blast loading [J]. Construction and Building Materials, 2018, 189: 420–437. DOI: 10.1016/j.conbuildmat.2018.09.005. [11] 赵卫坤, 沈峰, 夏益兵. 爆炸荷载下装配式钢筋混凝土梁动力响应及抗爆性能研究 [J]. 河北工程大学学报(自然科学版), 2022, 39(4): 18–25. DOI: 10.3969/j.issn.1673-9469.2022.04.003.ZHAO W K, SHEN F, XIA Y B. Study on dynamic response and anti-explosion performance of prefabricated reinforced concrete beams under blast load [J]. Journal of Hebei University of Engineering (Natural Science Edition), 2022, 39(4): 18–25. DOI: 10.3969/j.issn.1673-9469.2022.04.003. [12] 周广盼, 林志成, 王明洋, 等. 钢筋混凝土箱梁近场爆炸响应的试验与数值模拟 [J]. 爆炸与冲击, 2023, 43(7): 072201. DOI: 10.11883/bzycj-2022-0468.ZHOU G P, LIN Z C, WANG M Y, et al. Test and numerical study on the near-field explosion response of reinforced concrete box girder [J]. Explosion and Shock Waves, 2023, 43(7): 072201. DOI: 10.11883/bzycj-2022-0468. [13] KOU S X, ZHANG X H, LI W C, et al. Dynamic response parameter analysis of steel frame joints under blast loading [J]. Buildings, 2022, 12(4): 433. DOI: 10.3390/BUILDINGS12040433. [14] 梅志远, 朱锡, 刘润泉. 船用加筋板架爆炸载荷下动态响应数值分析 [J]. 爆炸与冲击, 2004, 24(1): 80–84.MEI Z Y, ZHU X, LIU R Q. Dynamic response researches of ship’s stiffened plate structure under explosive load [J]. Explosion and Shock Waves, 2004, 24(1): 80–84. [15] 张婧, 施兴华, 王善. 船用加筋板在水下接触爆炸作用下动态响应数值分析 [J]. 系统仿真学报, 2009, 21(24): 7929–7933.ZHANG J, SHI X H, WANG S. Dynamic response researches of ship stiffened plate structure subjected to underwater contact explosions [J]. Journal of System Simulation, 2009, 21(24): 7929–7933. [16] 方秦, 杜茂林, 陈力. 门上设置弹簧与阻尼器的防护门抗爆性能的理论与数值分析 [J]. 振动与冲击, 2010, 29(7): 83–87. DOI: 10.3969/j.issn.1000-3835.2010.07.018.FANG Q, DU M L, CHEN L. Theoretical and numerical investigation on blast-resistant properties of a blast door with springs and dampers [J]. Journal of Vibration and Shock, 2010, 29(7): 83–87. DOI: 10.3969/j.issn.1000-3835.2010.07.018. [17] 耿少波, 陈佳龙, 赵洲, 等. 基于双折线抗力模型的空爆荷载梁式构件振动位移研究 [J]. 爆炸与冲击, 2022, 42(10): 105102. DOI: 10.11883/bzycj-2021-0524.GENG S B, CHEN J L, ZHAO Z, et al. A study on vibration displacements of beam members under air blast loading based on the bilinear resistance model [J]. Explosion and Shock Waves, 2022, 42(10): 105102. DOI: 10.11883/bzycj-2021-0524. [18] 谢卫红, 董昊, 辛家宝. 碳纤维布加固钢筋混凝土梁的动力性能分析 [J]. 混凝土, 2009(7): 20–23. DOI: 10.3969/j.issn.1002-3550.2009.07.007.XIE W H, DONG H, XIN J B. Analysis of dynamic behavior of reinforced concrete beam with CFRPS [J]. Concrete, 2009(7): 20–23. DOI: 10.3969/j.issn.1002-3550.2009.07.007. [19] 董晓鹏, 易义君, 苏永贵. 爆炸荷载作用下约束刚度对梁端动力响应的影响 [J]. 国防交通工程与技术, 2016, 14(1): 33–36. DOI: 10.13219/j.gjgyat.2016.01.009.DONG X P, YI Y J, SU Y G. On the influence of the constrained stiffness on the dynamic response of the end of the beam under blasting loads [J]. Traffic Engineering and Technology for National Defense, 2016, 14(1): 33–36. DOI: 10.13219/j.gjgyat.2016.01.009. [20] HE H G, FAN H L. Explosion vibration mitigation of meta-plate with mass-spring metastructures [J]. Extreme Mechanics Letters, 2021, 42: 101108. DOI: 10.1016/j.eml.2020.101108. [21] HAO H. Predictions of structural response to dynamic loads of different loading rates [J]. International Journal of Protective Structures, 2015, 6(4): 585–605. DOI: 10.1260/2041-4196.6.4.585. [22] 耿少波, 罗干, 陈佳龙, 等. 阻尼对空爆荷载等效静载动力系数的影响 [J]. 爆炸与冲击, 2022, 42(2): 023201. DOI: 10.11883/bzycj-2021-0036.GENG S B, LUO G, CHEN J L, et al. Effect of damping on equivalent static load dynamic factor of air blast load [J]. Explosion and Shock Waves, 2022, 42(2): 023201. DOI: 10.11883/bzycj-2021-0036. [23] 方秦, 柳锦春. 地下防护结构 [M]. 北京: 中国水利水电出版社, 2010. -






 下载:
下载: