Numerical simulation of three-dimensional flow field characteristics in the chamber of large-caliber modular charge gun
-
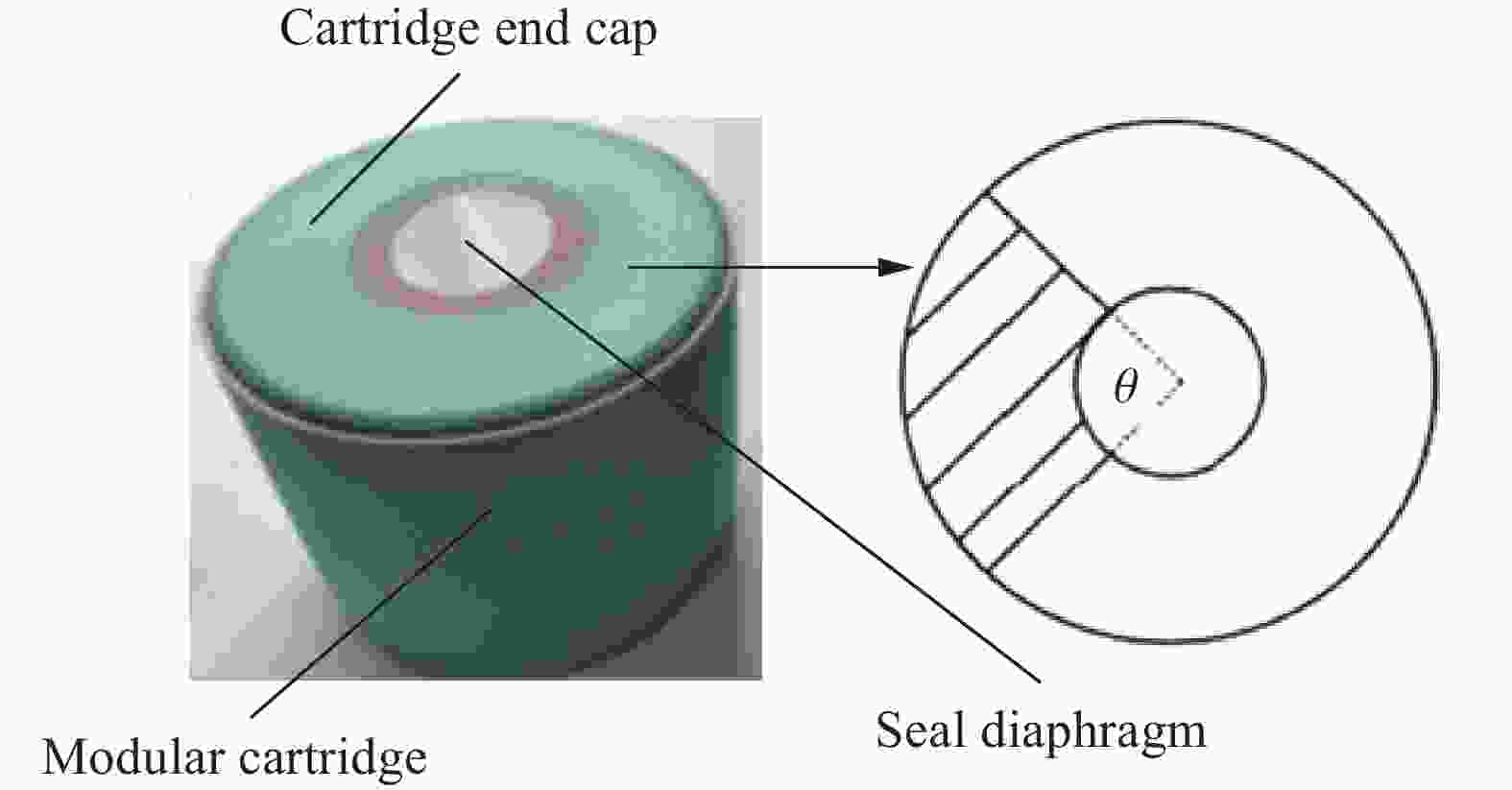
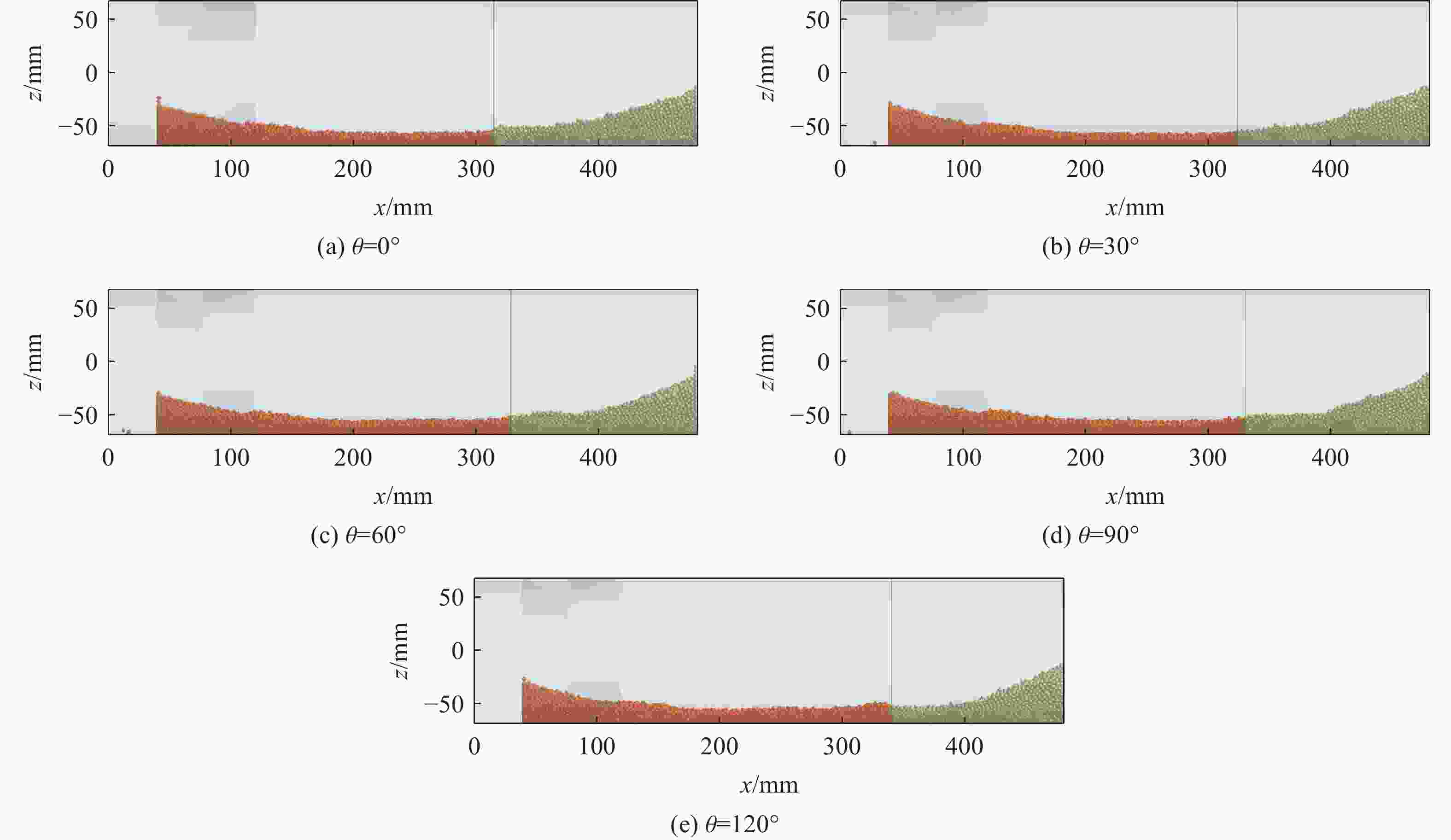
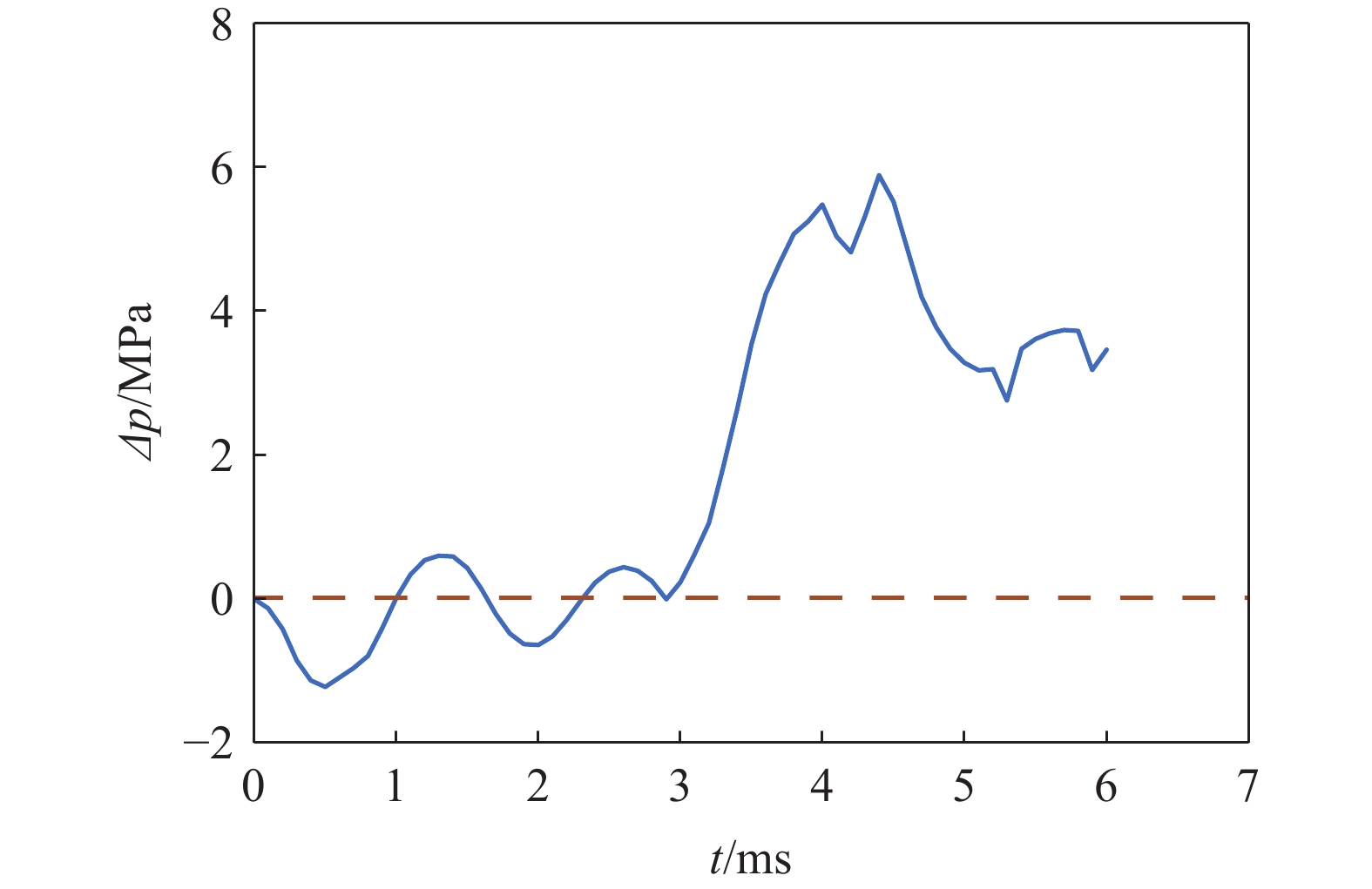
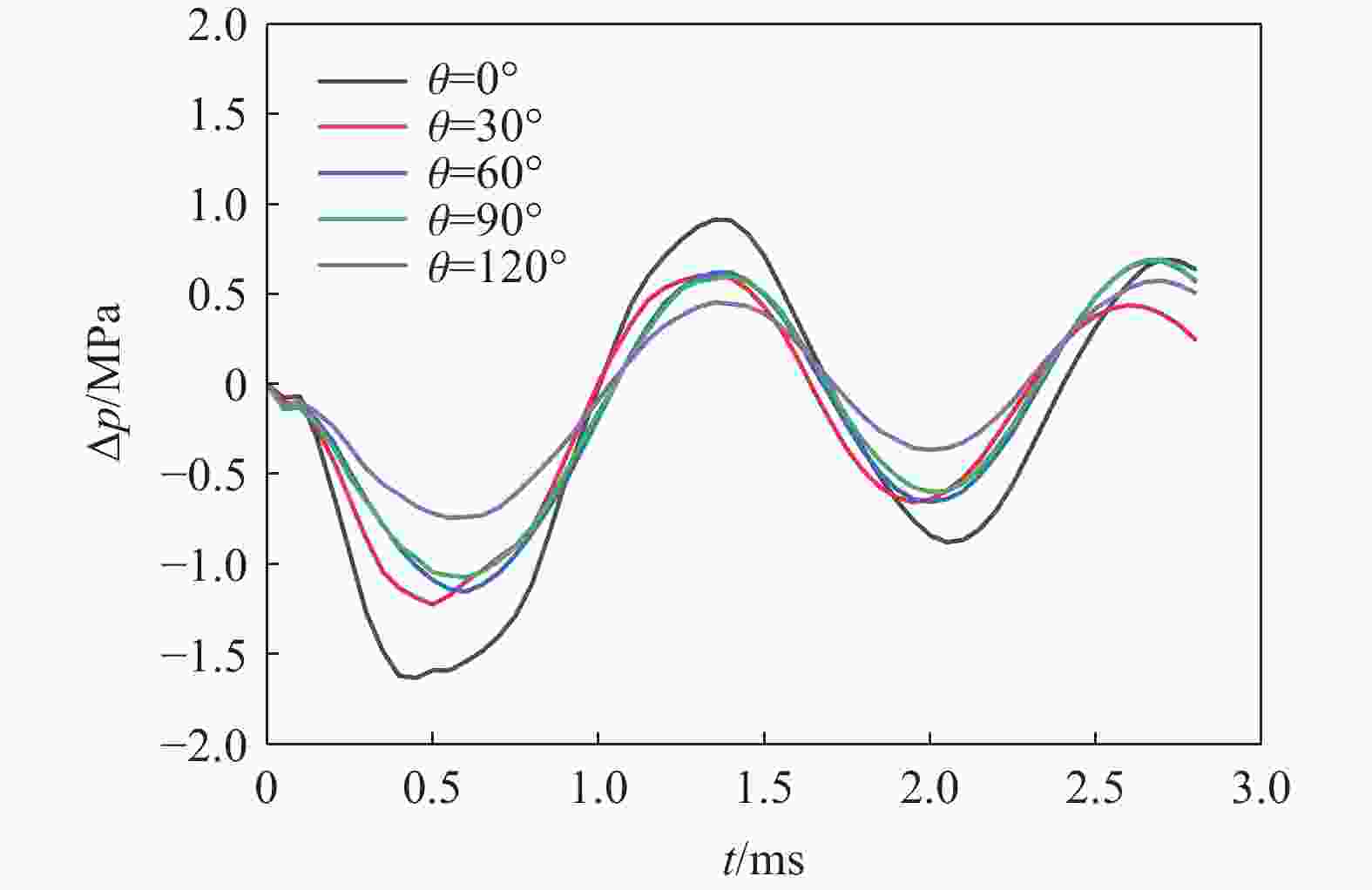
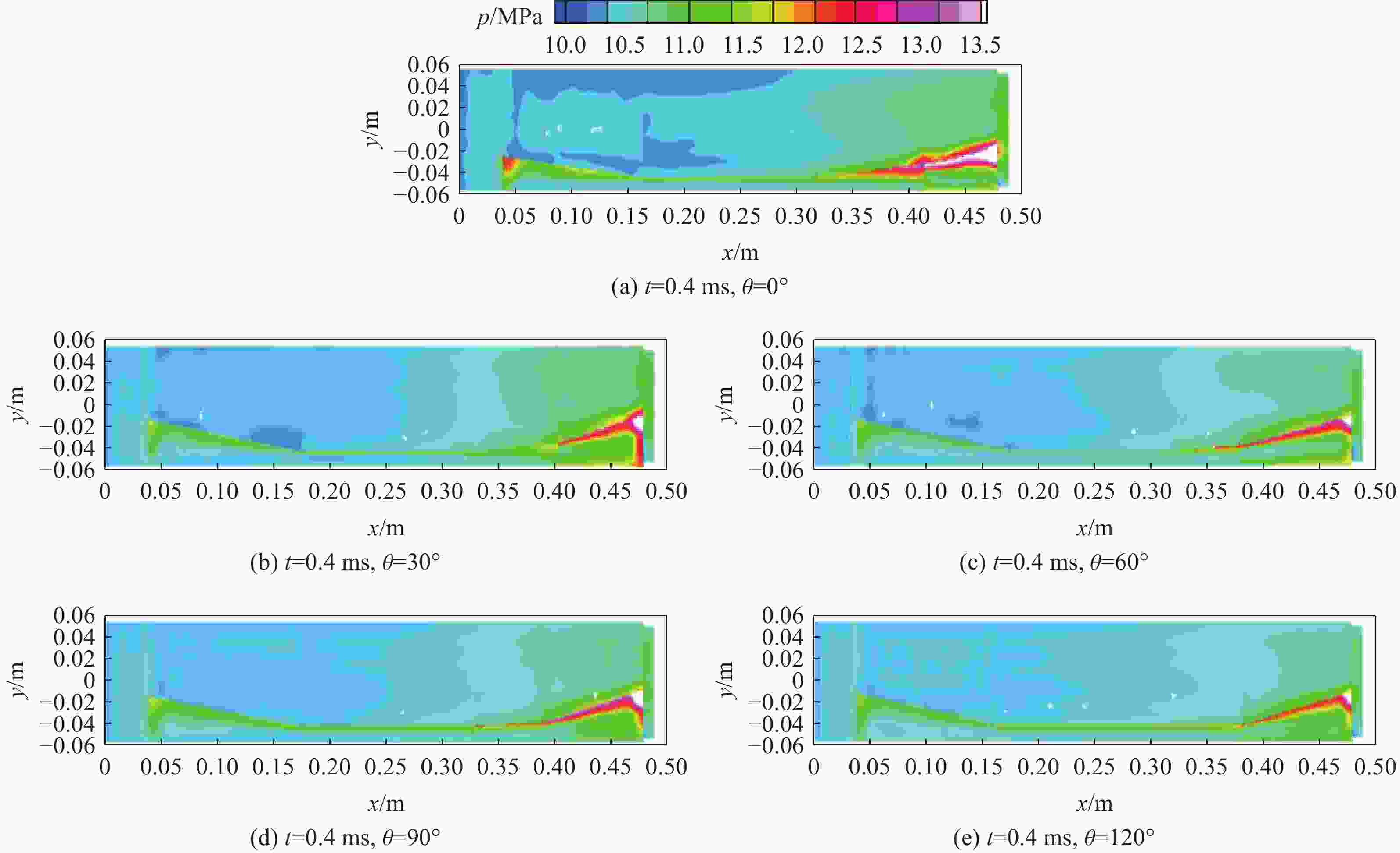
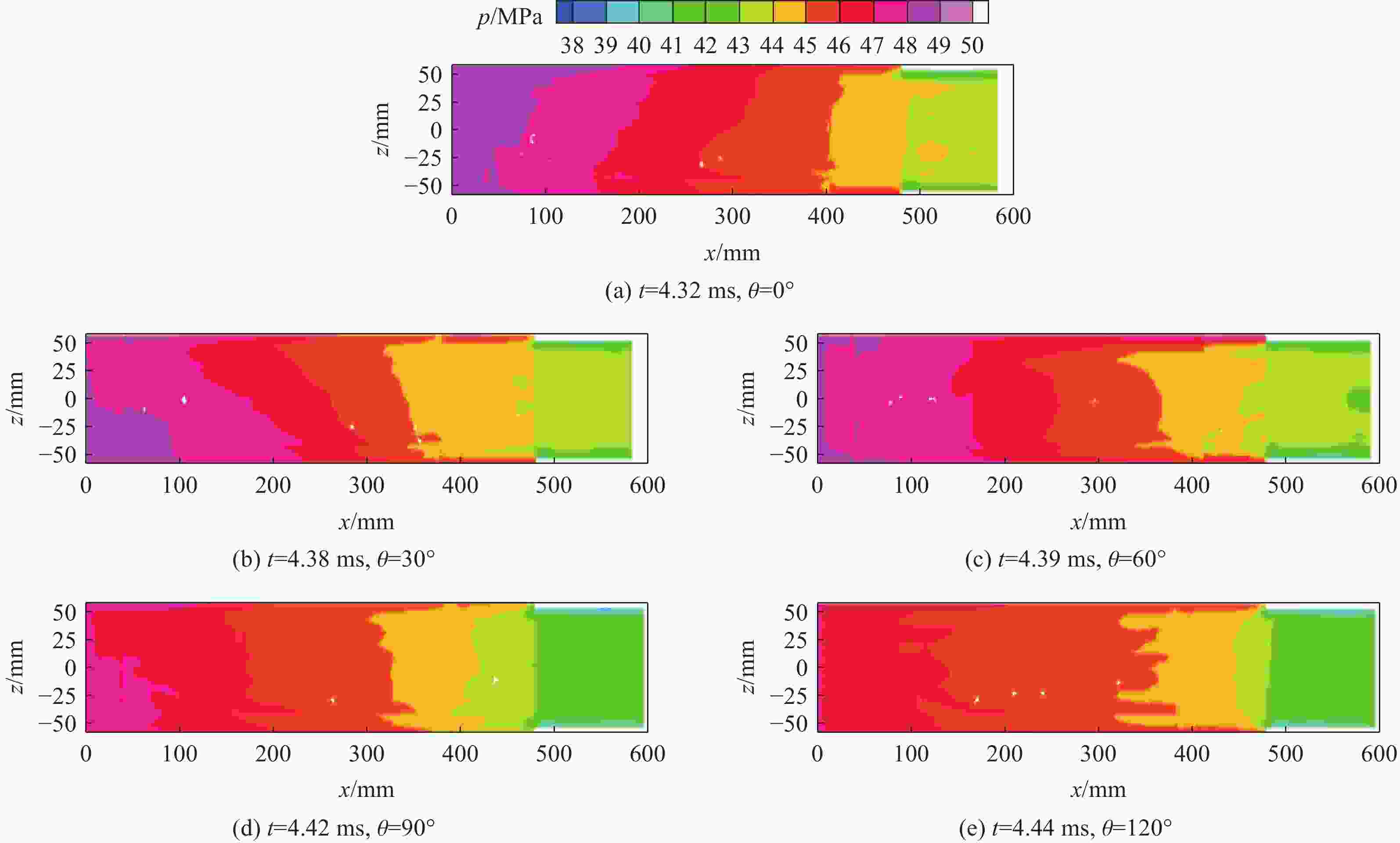
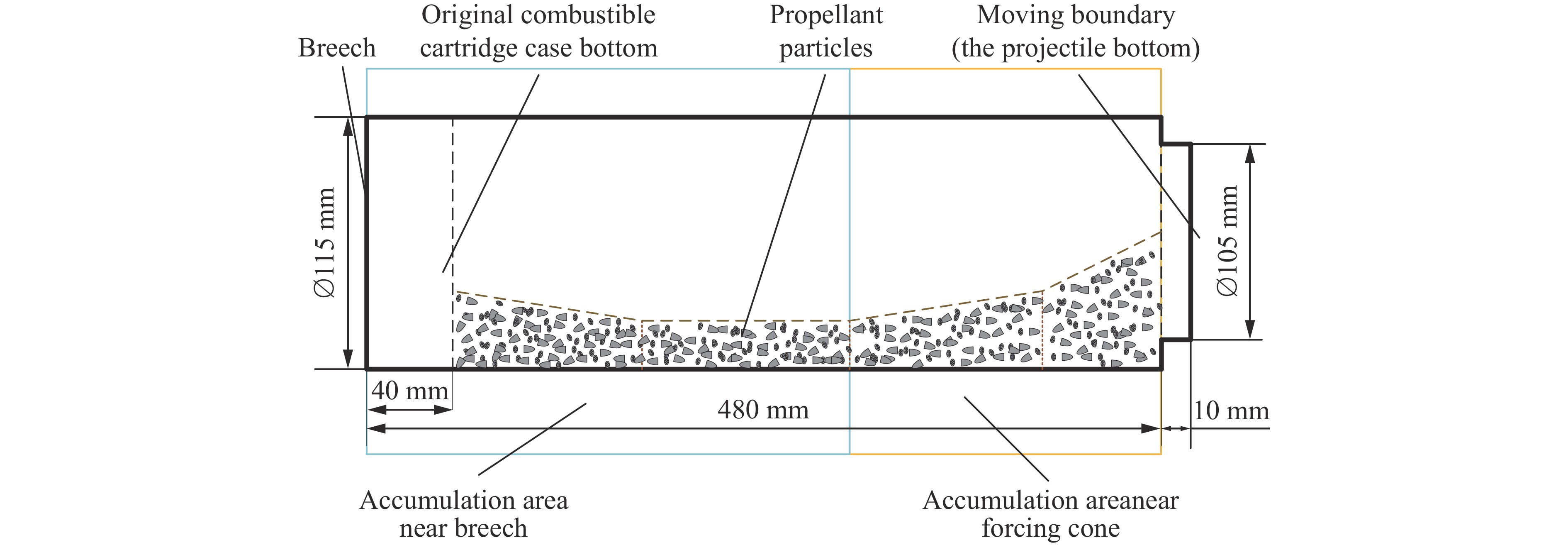
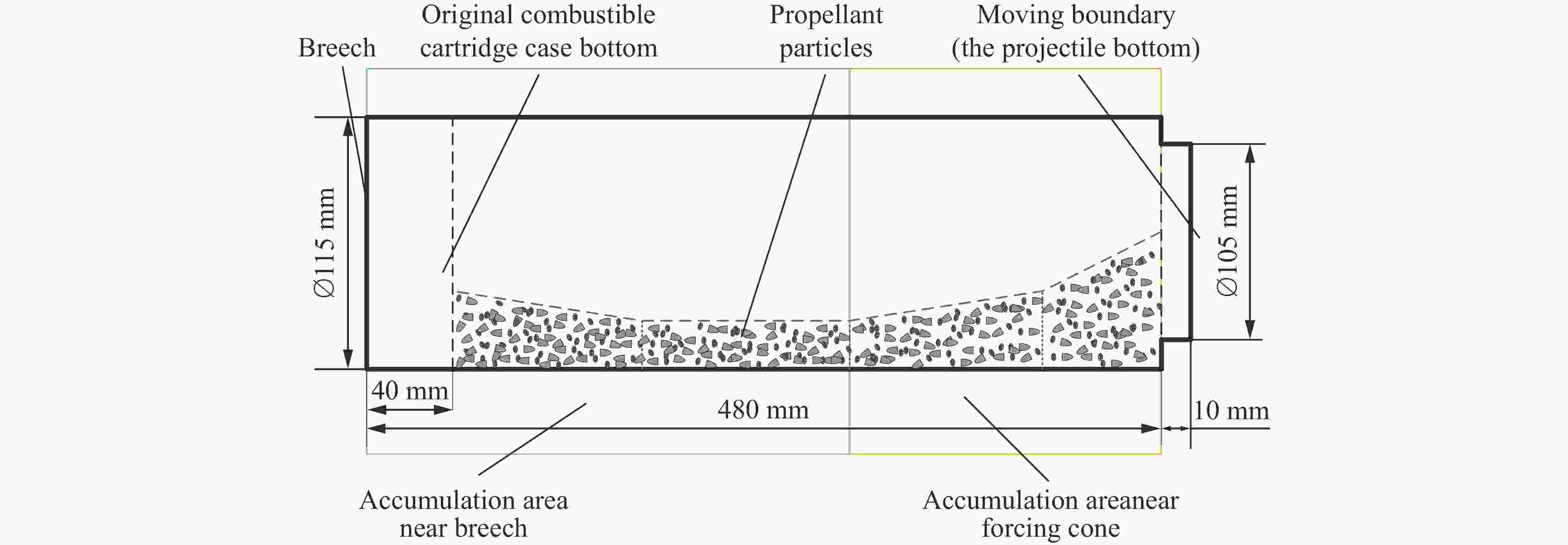
摘要: 为探索某大口径模块装药火炮内弹道过程中火药床堆积分布对膛内起始压力波三维空间特性的影响，建立了模块装药的三维气固两相燃烧动力学模型，对不同药盒端盖初始破口大小的工况开展了数值模拟，研究膛内复杂气固两相反应流场特性，分析了不同工况下药床的空间分布对膛内起始压力波特性的影响。结果表明，药盒端盖初始破口角度由0°增大至120°，则药粒飞散、沉降后，近膛底侧与近弹底侧区域的药粒占比差距由12.2%降至0.6%，弹底与膛底间初始负压差的绝对值由1.62 MPa降至0.76 MPa；弹丸启动时间由2.82 ms延至2.94 ms，弹底压力达到峰值所需时间由4.04 ms增至4.20 ms，端盖初始破口尺寸的差异会对膛内三维流场特性产生影响。
-
关键词:
- 模块装药 /
- 三维气固两相燃烧动力学模型 /
- 膛内流场 /
- 药床堆积分布 /
- 气固两相反应流
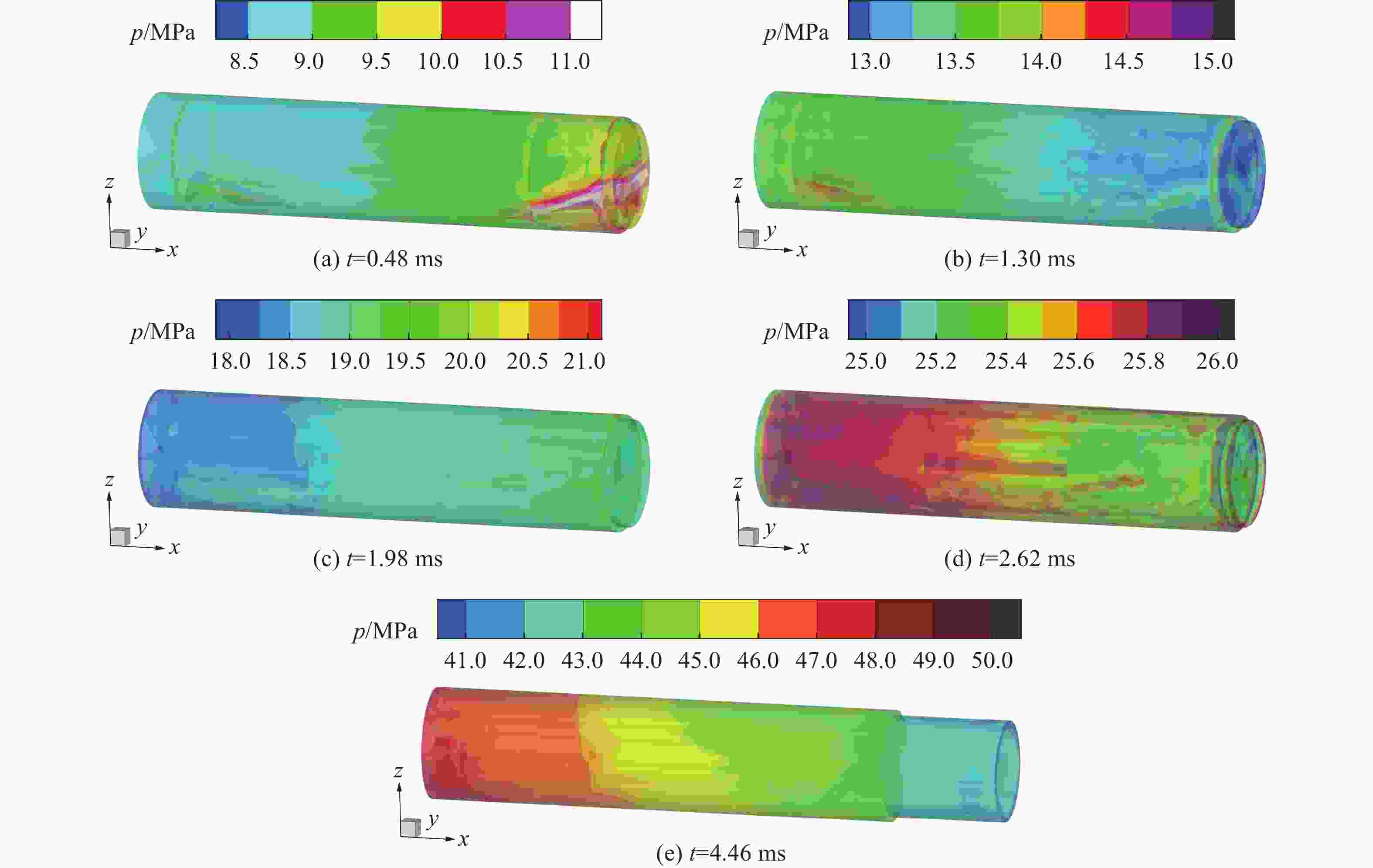
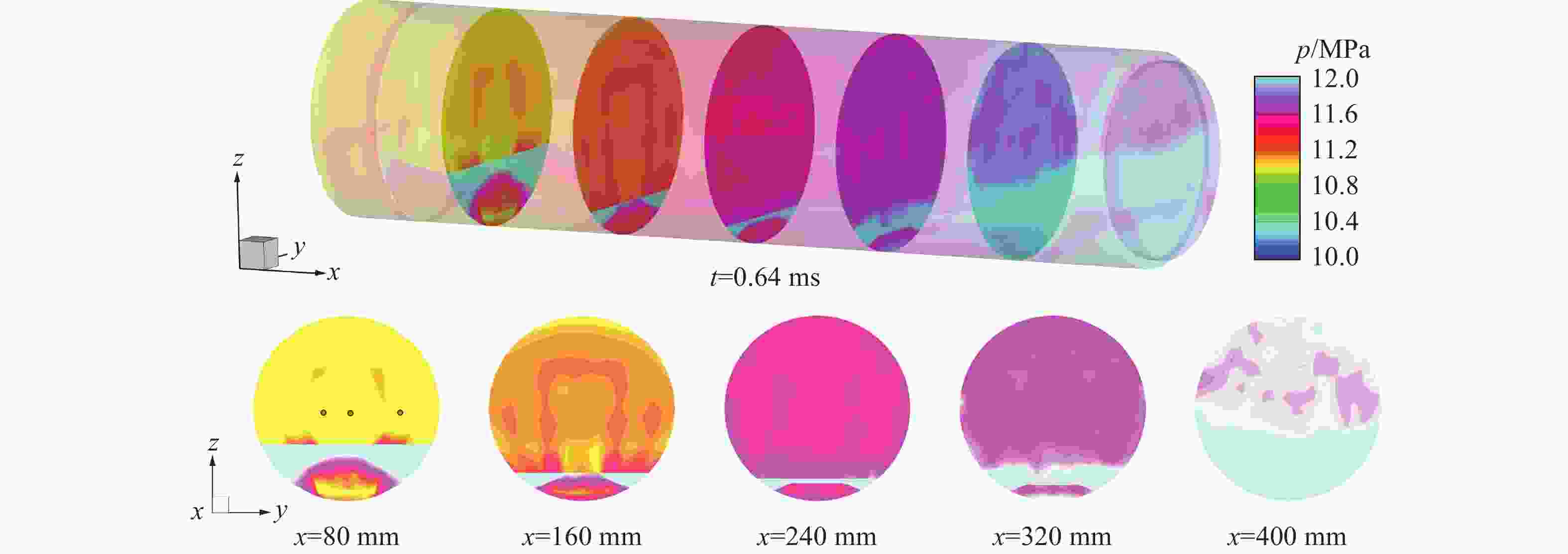
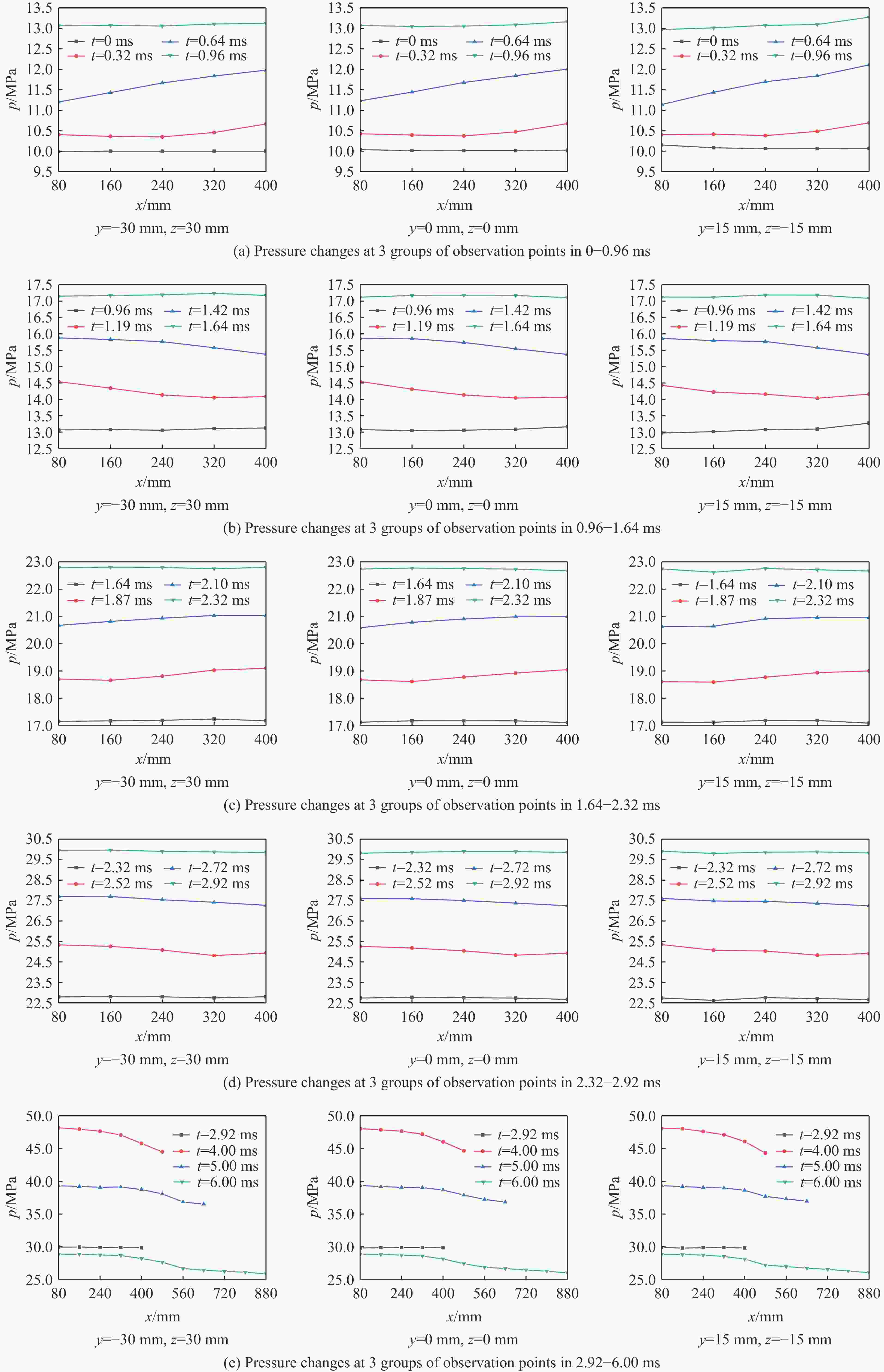
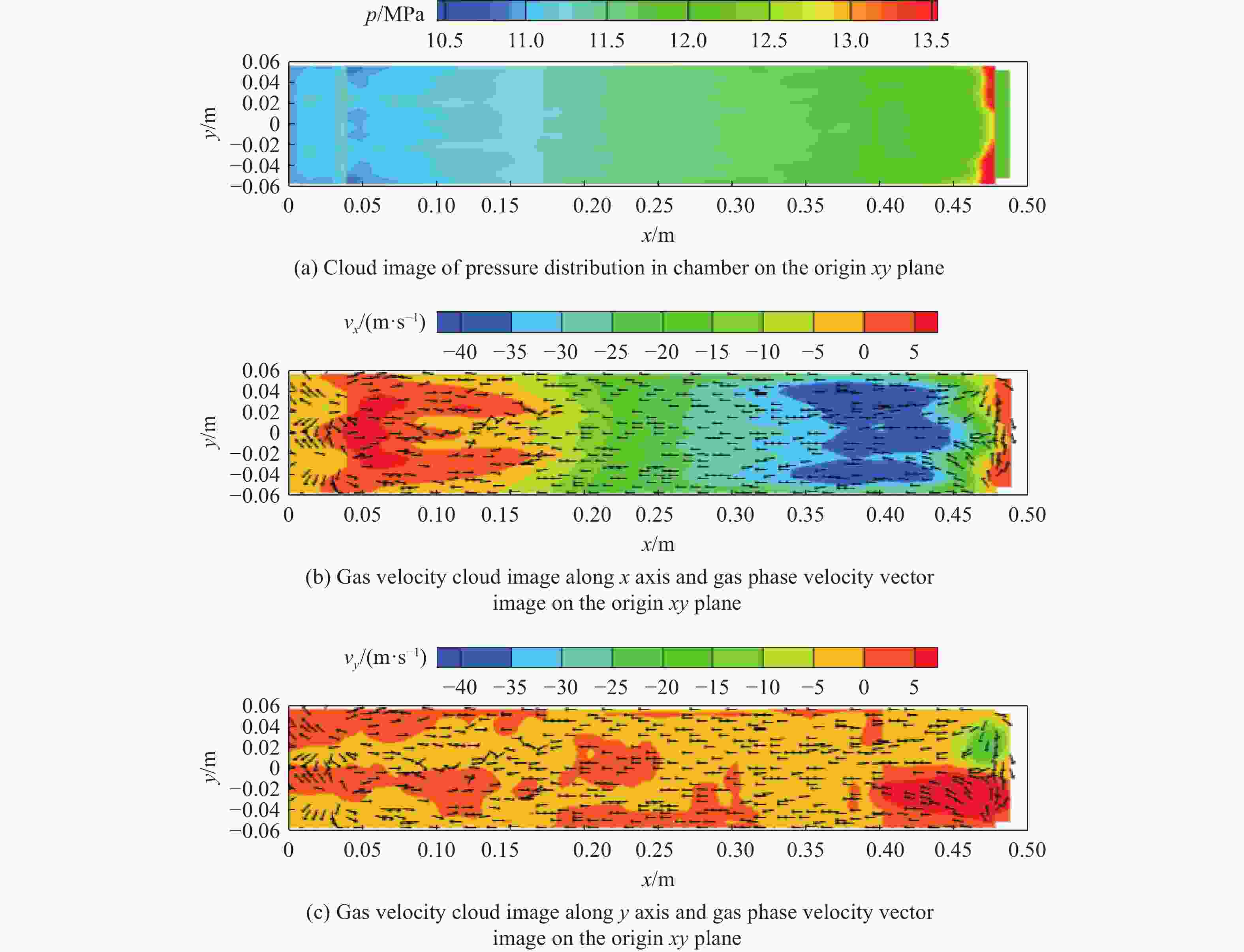
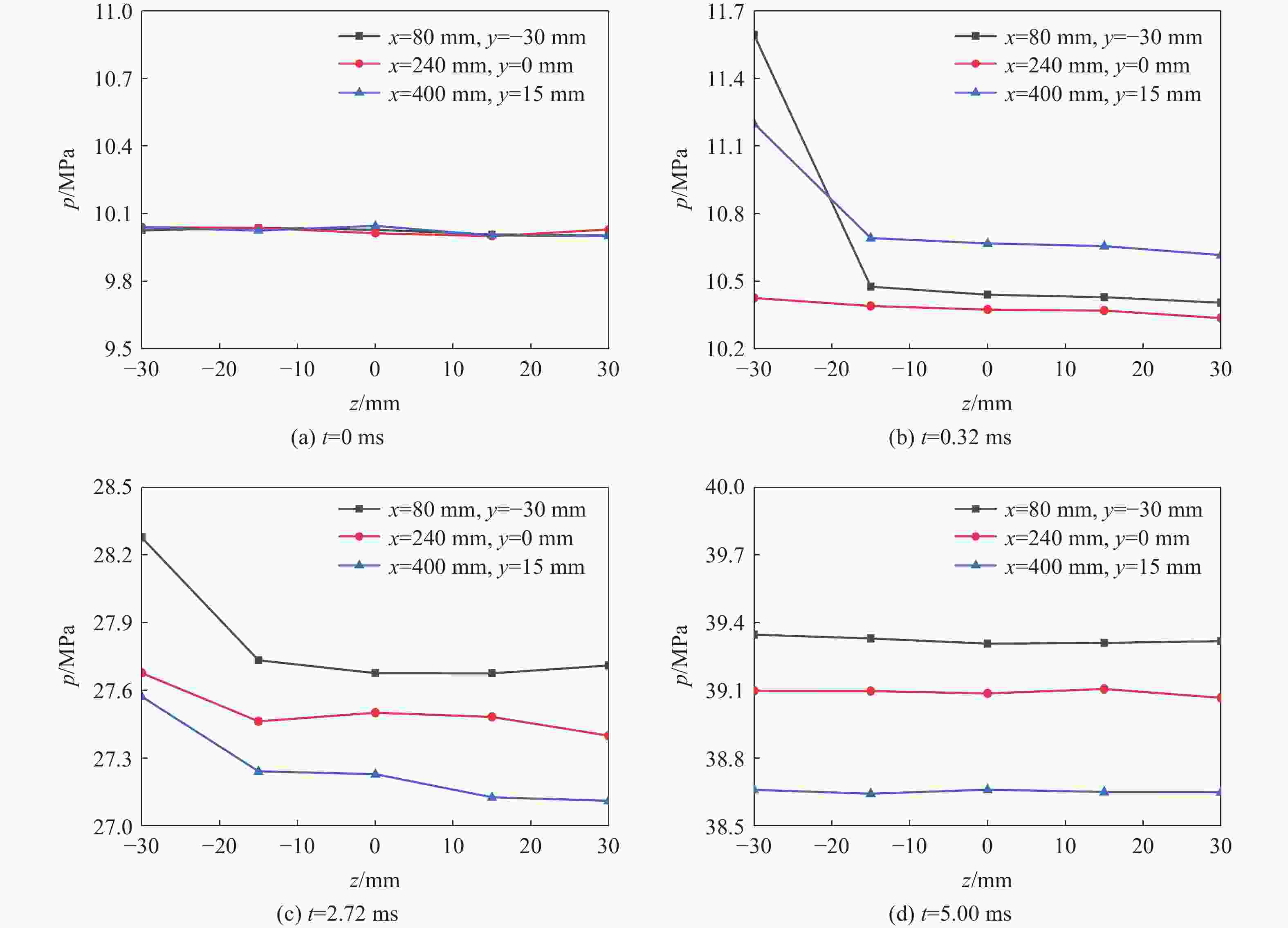
Abstract: To explore the influence of the propellant bed accumulation distribution on the three-dimensional characteristics of initial pressure wave in the chamber during the internal ballistic process of a large-caliber modular charge gun, a three-dimensional gas-solid two-phase combustion dynamic model of the modular charge was established. Firstly, solid powder particles were treated as discrete phase. Based on Euler-Lagrange method, the motion law and accumulation distribution of propellant particles under different initial broken sizes of cartridge end caps were simulated. Then, the propellant particles were treated as continuous phase and the evolution of pressure distribution in the chamber after combustion of the powder bed with different accumulation distribution was numerically simulated using the Euler-Euler method. The results show that the characteristics of the three-dimensional flow field in the bore are affected by the difference of the initial fracture size of the cartridge end cap. When the initial breaking angle of the cartridge end cap increases from 0° to 120°, the difference of the propellant particles in the area near breech and the area near forcing cone decreases from 12.2% to 0.6% after the dispersion and settlement of the propellant particles. Additionally, the absolute value of the initial negative pressure difference between the breech and the forcing cone decreases from 1.62 MPa to 0.76 MPa. The start-up time of the bullet is extended from 2.82 ms to 2.94 ms, and the time required for the forcing cone pressure to reach its peak is increases from 4.04 ms to 4.20 ms. At the same time, complex three-dimensional pressure fluctuations were observed in the chamber. Before the bullet movement, the chamber pressure can be divided into four pressure evolution characteristics along the X-axis direction, presenting the pressure with no changing, gradually decreasing, first decreasing and then increasing, as well as gradually increasing. After the bullet movement, the chamber pressure consistently decreases along the X-axis direction. However, along the Y-axis direction, the pressure in the chamber remains essentially unchanged before and after the bullet movement. The pressure in the chamber can be also divided into four pressure evolution characteristics along the Z-axis direction, presenting basically maintaining a constant level, gradually decreasing, first decreasing and then increasing, first decreasing and then increasing and then decreasing. The research results have some reference value for the interior ballistic safety analysis of modular charge guns. -
图 1 三维气固两相燃烧计算模型
Figure 1. Three-dimensional gas-solid two-phase combustion calculation model
图 2 3种网格尺寸划分平均膛压计算结果比较
Figure 2. Comparison of the calculation results of average chamber pressure divided by three types of grid sizes
图 4 实验膛底p-t和Δp-t曲线与计算结果的比较
Figure 4. Comparison of experimental and simulation results of the p-t curve at breech and the Δp-t curve between forcing cone and breech
图 9 各特征时刻膛内压力三维空间分布
Figure 9. 3D spatial distribution of pressure in chamber at each characteristic time
图 10 火炮膛内观测点的三维空间分布
Figure 10. Three-dimensional spatial distribution of observation points in chamber
图 12 火药燃烧后膛内压力梯度及气相运动规律示意图
Figure 12. Schematic diagrams of pressure gradient and gas phase movement in the chamber after propellant combustion
图 14 弹丸运动前各工况弹底与膛底的压差曲线
Figure 14. Pressure difference curves between forcing cone and breech different conditions before the bullet movement
图 15 弹丸启动前各工况于过原点XZ切面上的压力梯度云图
Figure 15. Cloud image of pressure gradient at the origin XZ plane before the bullet movement under each condition
图 16 弹丸启动后各工况于过原点XZ切面上的压力梯度云图
Figure 16. The pressure gradient cloud image of each condition on the origin XZ plane after the bullet movement
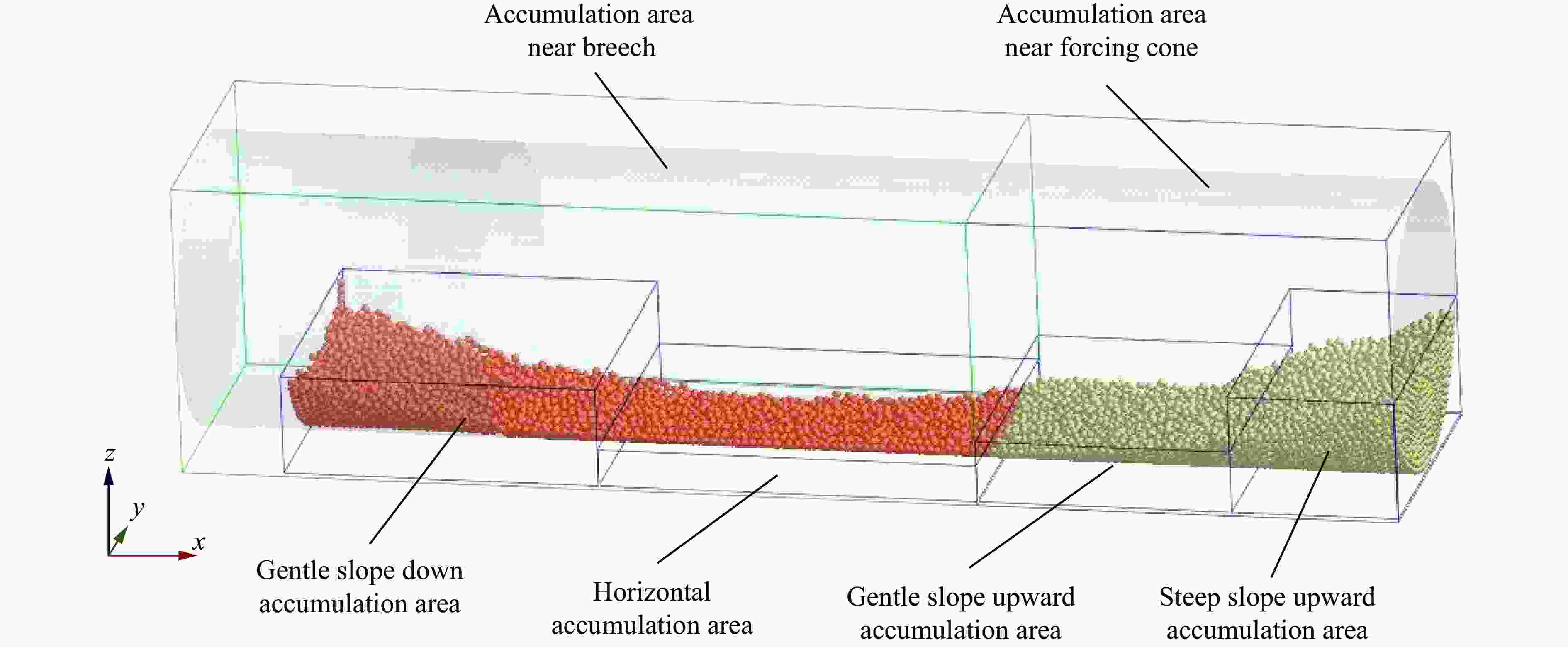
表 1 不同工况下火药床形状特征参数
Table 1. Shape characteristic parameters of propellant bed under different working conditions
工况 端盖初始破口
角度/(º)近膛底区域
长度/mm近弹底区域
长度/mm近膛底区域
厚度/mm近弹底区域
厚度/mm近膛底区域
药粒占比/%近弹底区域
药粒占比/%1 0 314 166 15.1 28.1 43.9 56.1 2 30 324 156 18.6 27.8 44.8 55.2 3 60 328 152 19.2 27.0 47.1 52.9 4 90 333 147 19.7 25.6 48.7 51.3 5 120 340 140 20.1 24.6 50.3 49.7 
下载: 导出CSV
表 2 各组压力观测点处压力的相对平均偏差
Table 2. The relative mean deviation of pressure at each pressure observation point
时间/ms $\delta p$(X=80 mm
Z=30 mm)/%$\delta p$(X=240 mm
Z=0 mm)/%$\delta p$(X=400 mm
Z=−15 mm)/%0.00 0.035 0.015 0.050 0.48 0.075 0.083 0.185 0.96 0.056 0.055 0.191 1.30 0.064 0.040 0.232 1.64 0.034 0.041 0.140 1.98 0.051 0.069 0.193 2.32 0.031 0.054 0.079 2.62 0.048 0.082 0.095 2.92 0.063 0.052 0.163 4.46 0.029 0.013 0.139 6.00 0.077 0.035 0.132
下载: 导出CSV
表 3 各工况弹丸启动时刻及弹底压力达到峰值所需时间
Table 3. The bullet starting time and the time required for the bottom pressure to reach the peak under each working condition
药盒端盖破口
夹角/(º)弹丸启动
压力/MPa弹丸启动
时刻/ms弹底压力
峰值/MPa弹底压力达到峰值
所需时间/ms0 30.00 2.82 44.24 4.04 30 30.00 2.88 43.92 4.06 60 30.00 2.89 43.82 4.08 90 30.00 2.92 44.27 4.14 120 30.00 2.94 43.84 4.20
下载: 导出CSV
表 4 特征时刻各工况弹丸位移
Table 4. Bullet displacements at characteristic times under different working conditions
药盒端盖破口夹角/(º) L/mm t=2.94 ms t=3.49 ms t=4.04 ms t=4.12 ms t=4.20 ms t=5.10 ms t=6.00 ms 0 0.54 18.44 65.13 74.63 84.83 244.15 423.58 30 0.16 15.35 58.56 67.50 77.13 223.78 410.12 60 0.09 14.45 56.40 65.11 74.52 219.10 403.39 90 0.02 13.05 53.49 61.96 71.13 215.46 401.76 120 0.00 12.22 51.65 59.53 68.92 212.53 399.70
下载: 导出CSV
表 5 特征时刻各工况弹丸的加速度
Table 5. Bullet accelerations at characteristic times under different working conditions
药盒端盖破口夹角/(º) a/(m·s−2) t=2.94 ms t=3.49 ms t=4.04 ms t=4.12 ms t=4.20 ms t=5.10 ms t=6.00 ms 0 78336 94929 110507 109684 108052 53903 32037 30 76957 92420 109887 109008 108389 54387 33754 60 76354 91012 109072 109656 109000 54724 34373 90 75619 90273 107845 110463 110569 54871 34562 120 75081 89268 106811 108438 110787 55036 34771
下载: 导出CSV
-
[1] 王彬, 周涛, 胡志东, 等. 全可燃药筒发展现状及前景 [J]. 兵工自动化, 2019, 38(8): 88–90. DOI: 10.7690/bgzdh.2019.08.026.WANG B, ZHOU T, HU Z D, et al. Combustible cartridge case development current situation and its prospects [J]. Ordnance Industry Automation, 2019, 38(8): 88–90. DOI: 10.7690/bgzdh.2019.08.026. [2] 董凤鸣, 刘东尧. 模块药盒装填位置及药粒散布状态对内弹道特性影响的数值模拟研究 [J]. 弹道学报, 2023, 35(4): 20–26. DOI: 10.12115/j.issn.1004-499X(2023)04-003.DONG F M, LIU D Y. Numerical simulation on the influence of filling position of modular cartridge and particle distribution state on internal ballistic characteristics [J]. Journal of Ballistics, 2023, 35(4): 20–26. DOI: 10.12115/j.issn.1004-499X(2023)04-003. [3] QIAN H Y, YU Y G, LIU J. Effects of module number and firing condition on charge thermal safety in gun chamber [J]. Defence Technology, 2022, 18(1): 27–37. DOI: 10.1016/j.dt.2020.11.003. [4] BRUNET L E, FITAS T, CUVELIER S, et al. Deep and machine learning architecture for high accuracy prediction of interior ballistics for modular charges [J]. Propellants, Explosives, Pyrotechnics, 2023, 48(10): e202300151. DOI: 10.1002/prep.202300151. [5] 王泽山. 模块装药技术及其进展 [J]. 含能材料, 2004, 12(S1): 122. DOI: 10.3969/j.issn.1006-9941.2004.z1.031.WANG Z S. Module charging technology and its progress [J]. Chinese Journal of Energetic Materials, 2004, 12(S1): 122. DOI: 10.3969/j.issn.1006-9941.2004.z1.031. [6] 王育维, 郭映华, 董彦诚, 等. 可燃容器对小号模块装药压力波影响的研究 [J]. 火炮发射与控制学报, 2016, 37(2): 31–35,45. DOI: 10.19323/j.issn.1673-6524.2016.02.007.WANG Y W, GUO Y H, DONG Y C, et al. Study of combustible case effects on pressure waves for low-zone of bi-modular charge [J]. Journal of Gun Launch and Control, 2016, 37(2): 31–35,45. DOI: 10.19323/j.issn.1673-6524.2016.02.007. [7] 聂奎. 等离子体点火对模块装药内弹道性能影响的研究 [D]. 南京: 南京理工大学, 2010. DOI: 10.7666/d.Y1698160.NIE K. Studies on influence of plasma ignition to the interior ballistic performance of the gun with modular charges [D]. Nanjing: Nanjing University of Science and Technology, 2010. DOI: 10.7666/d.Y1698160. [8] WOODLEY C. On the use of accurate ignition and combustion models in internal ballistics gun codes [J]. Chinese Journal of Explosives and Propellants, 2018, 41(2): 117–121. DOI: 10.14077/j.issn.1007-7812.2018.02.002. [9] 陈安, 余永刚. 两模块装药点传火过程及药粒散布特性 [J]. 爆炸与冲击, 2021, 41(7): 072301. DOI: 10.11883/bzycj-2020-0215.CHEN A, YU Y G. Ignition process and propellant grains distribution of the two-module charge [J]. Explosion and Shock Waves, 2021, 41(7): 072301. DOI: 10.11883/bzycj-2020-0215. [10] 森思义, 王浩, 陶如意. 基于CE/SE方法对模块装药点传火过程的数值模拟及特性研究 [J]. 含能材料, 2022, 30(7): 744–751. DOI: 10.11943/CJEM2022002.SEN S Y, WANG H, TAO R Y. Numerical simulation and characteristics analysis on lgnition and flame-propagation process of modular charge based on CE/SE method [J]. Chinese Journal of Energetic Materials, 2022, 30(7): 744–751. DOI: 10.11943/CJEM2022002. [11] 冯渊, 王育维, 朱文芳, 等. 基于CE/SE方法的某大口径火炮模块装药内弹道数值模拟 [J]. 火炮发射与控制学报, 2023, 44(6): 51–59. DOI: 10.19323/j.issn.1673-6524.2023.06.008.FENG Y, WANG Y W, ZHU W F, et al. Numerical simulation on interior ballistic of a large caliber cannon with modular propellant charge based on CE/SE method [J]. Journal of Gun Launch & Control, 2023, 44(6): 51–59. DOI: 10.19323/j.issn.1673-6524.2023.06.008. [12] MA C J, ZHANG X B. Interior ballistic modeling and simulation for different charge zones in modular charge system [J]. Journal of Applied Mechanics, 2013, 80(3): 031404. DOI: 10.1115/1.4023314. [13] CHENG S S, TAO R Y, XUE S, et al. Two-phase flow characteristics of different charging structure in ignition and flame-spreading [J]. Combustion Theory and Modelling, 2021, 25(4): 751–764. DOI: 10.1080/13647830.2021.1937703. [14] CHENG S S, TAO R Y, XUE S, et al. The particle element method to obtain parameter distributions of two-phase reactive flow in a propulsion combustion system [J]. Combustion Science and Technology, 2024, 196(5): 730–752. DOI: 10.1080/00102202.2022.2101104. [15] MA T Y, WANG H, TAO R Y. Investigation of combustion process in a modular charge system with a primer gap [J]. AIP Advances, 2023, 13(11): 115018. DOI: 10.1063/5.0170254. [16] CHEN A, YU Y G. Three-dimensional particle-scale investigation of transient gas-solid flow characteristics in the propulsion system with a complex charge structure [J]. Physics of Fluids, 2024, 36(8): 085122. DOI: 10.1063/5.0216737. [17] 杨旭光, 余永刚, 陈安. 单模块装药点火燃烧过程中端盖破裂形态对药粒散布的影响 [J]. 火炸药学报, 2022, 45(4): 582–589. DOI: 10.14077/j.issn.1007-7812.202201005.YANG X G, YU Y G, CHEN A. Effect of rupture form of end cover on grain dispersion during ignition and combustion of single module charge [J]. Chinese Journal of Explosives and Propellants, 2022, 45(4): 582–589. DOI: 10.14077/j.issn.1007-7812.202201005. [18] 金志明. 枪炮内弹道学 [M]. 北京: 北京理工大学出版社, 2004.JIN Z M. Interior ballistics of guns [M]. Beijing: Beijing Institute of Technology Press, 2004. [19] 陆中兵, 周彦煌. 模块装药火炮膛内两相燃烧模型及压力波模拟 [J]. 爆炸与冲击, 1999, 19(3): 269–273. DOI: 10.11883/1001-1455(1999)03-0269-5.LU Z B, ZHOU Y H. Two phase-combustion model and numerical simulation of pressure wave in the gun with modular charges [J]. Explosion and Shock Waves, 1999, 19(3): 269–273. DOI: 10.11883/1001-1455(1999)03-0269-5. -
计量
- 文章访问数: 126
- HTML全文浏览量: 16
- PDF下载量: 40
- 被引次数: 0