Simulation analysis and experimental verification of dynamic mechanical properties of white sandstone based on different constitutive models
-
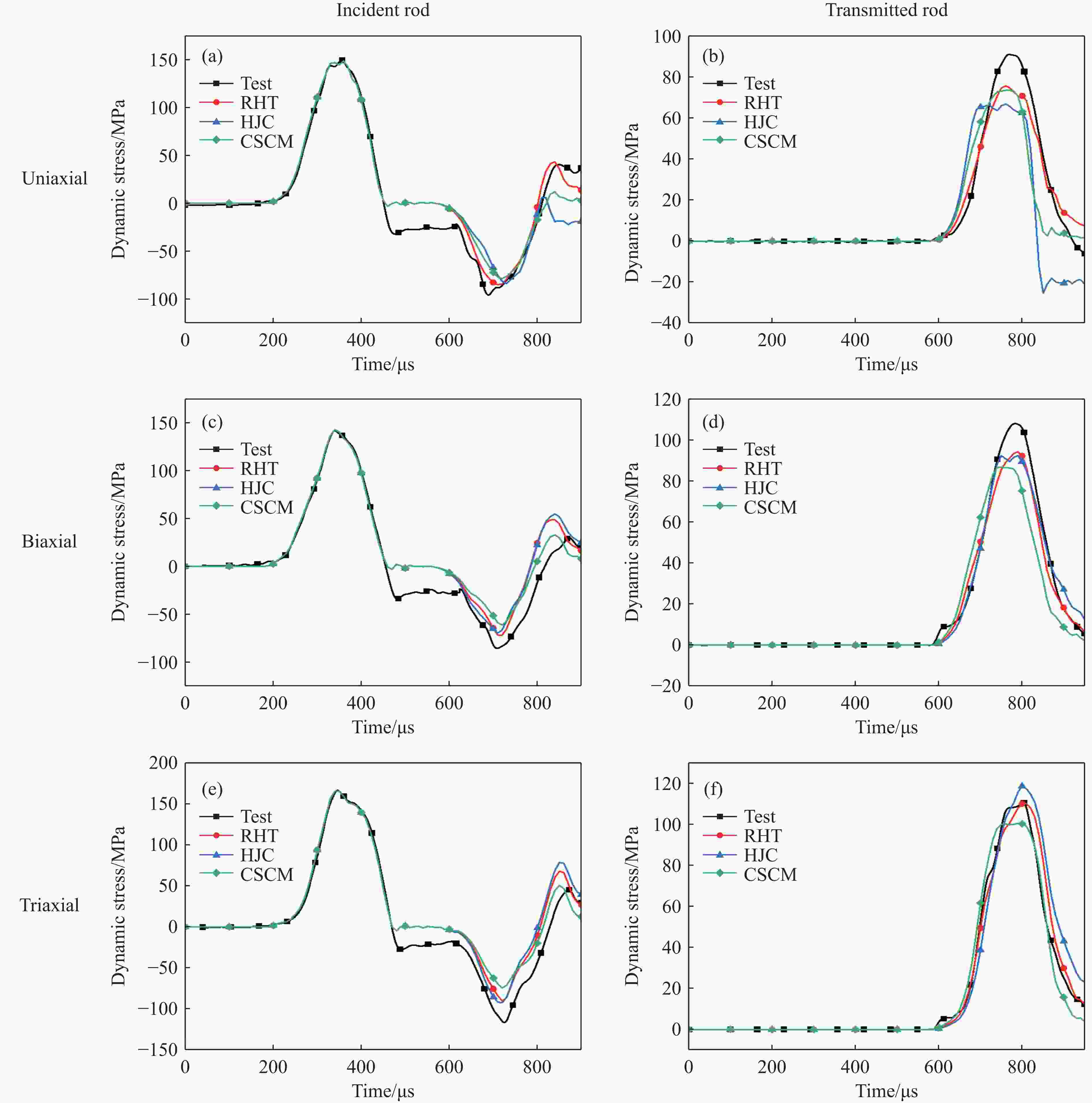
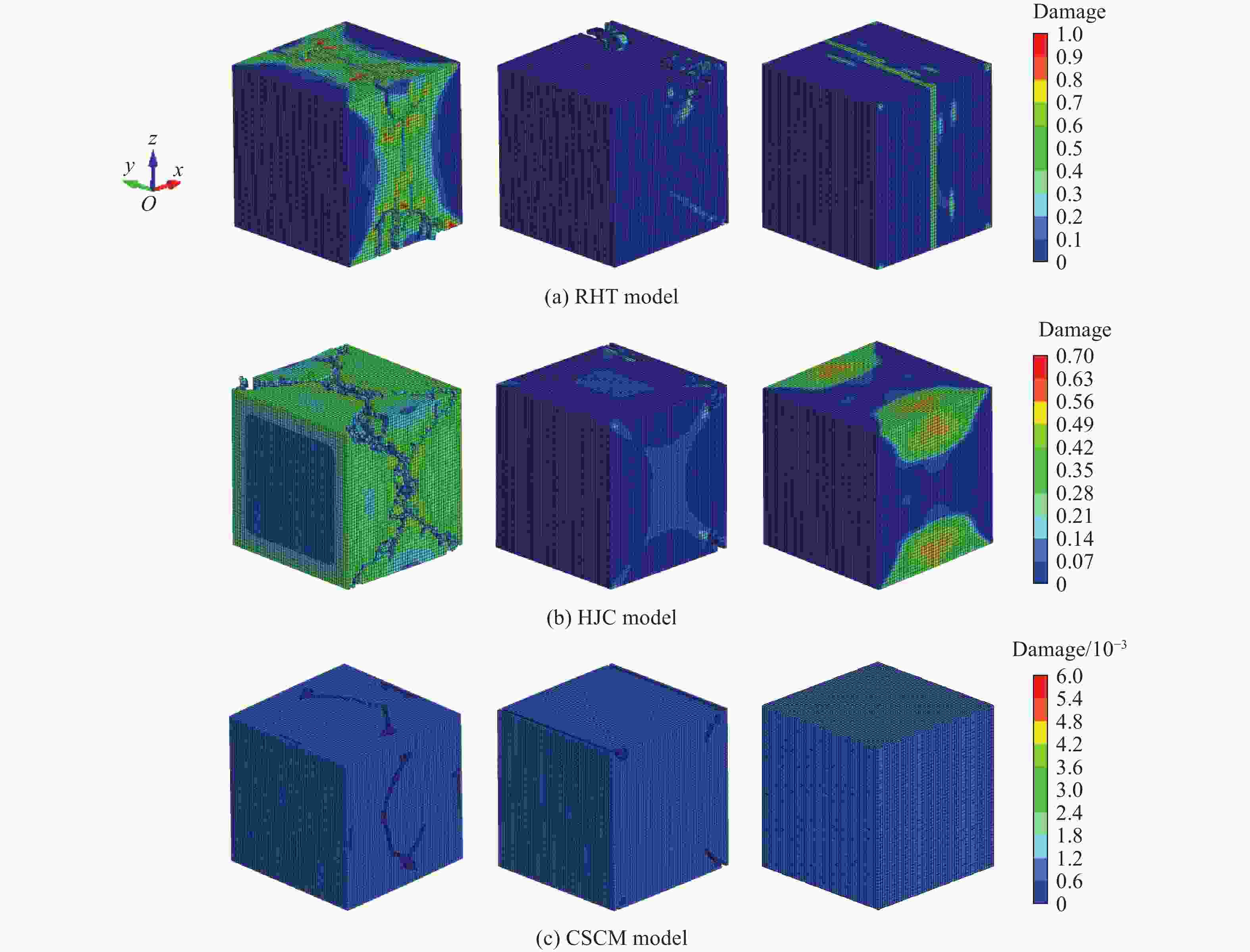
摘要: 以三维霍普金森杆实验结果为基准，以某煤矿下的白砂岩作为研究对象，采用Riedel-Hiermaier-Thoma (RHT) 模型、Holmquist-Johnson-Cook (HJC)模型和连续面帽盖模型（continuous surface cap model，CSCM)等3种典型岩石本构模型开展仿真分析，对白砂岩在单轴、双轴和三轴状态下的动态力学性能进行对比和验证。结果表明，白砂岩试件的剪切破坏损伤随预应力的提高而减弱，三轴状态下岩石受到的损伤明显弱于单轴和双轴状态下的；基于RHT本构模型的仿真结果在应力波波形、峰值应力、峰值应变以及损伤程度上，与实验结果更贴合；单、双轴状态下RHT本构模型的仿真结果在反射波段的波峰应力与实验结果的相对偏差分别为3.5%和13.6%，透射波段的波峰应力与实验结果的相对偏差最小，且峰值应力和应变在数值上更接近实验值。RHT本构模型仿真结果中的损伤状态与实验结果中的损伤状态相似，单轴下呈现U形损伤特征；HJC本构模型仿真结果中白砂岩试件在单轴下则呈现出大范围V形损伤特征，且发生断裂；CSCM本构模型仿真结果中白砂岩试件仅在表面发生损伤，损伤范围较小。在能量吸收和耗散方面，3种本构模型仿真结果的差异性较小，3种本构模型仿真得到的入射能、反射能和透射能基本保持一致。此外，白砂岩试件的损伤程度随冲击速度的升高而提高。随冲击速度的升高，3种本构模型对损伤的模拟结果均增大，损伤特征均被保留。Abstract: The dynamic mechanical properties of deep rocks are critical to understanding geological processes and optimizing resource extraction. Accurately understanding the dynamic mechanical properties of deep rocks not only provides insights into the geological processes and evolution of Earth's interior, but also offers a theoretical basis for the effective extraction of deep minerals and energy. In this study, the dynamic mechanical behavior of white sandstone from a coal mine was experimentally and numerically analyzed under uniaxial, biaxial, and triaxial stress conditions. Numerical simulations based on three constitutive models consisting of the Riedel-Hiermaier-Thoma (RHT) model, the Holmquist-Johnson-Cook (HJC) model, and the continuous surface cap model (CSCM), were validated by using experimental results from three-dimensional Hopkinson bar tests. The results indicate that the shear failure damage of white sandstone specimens decreases with the increasing prestress, with triaxial stress conditions yielding significantly lower damage than uniaxial or biaxial conditions. Among the three models, the RHT constitutive model demonstrates the closest agreement with the experimental results in terms of stress waveforms, peak stress, peak strain, and damage degree. Compared with the experimental data, the RHT model exhibits a stress peak deviation rate of 3.5% and 13.6% for the reflected wave under uniaxial and biaxial conditions, respectively, while the stress peak deviation rate for the transmitted wave is the lowest. Additionally, the peak stress and strain values predicted by the RHT model are numerically closer to the experimental results. The damage state predicted by the RHT model also aligns well with the experimental observations: under uniaxial loading, the damage exhibits a U-shaped pattern, whereas the HJC model showed a larger V-shaped damage pattern and fracture, and the CSCM model displayed surface damage with a smaller affected area. In terms of energy absorption and dissipation, the simulation results based on the three constitutive models shows minimal differences. The incident, reflected, and transmitted energy values are nearly identical across all three models. In addition, the damage degree of the white sandstone specimens increases with the impact velocity. The damage simulation results of the three constitutive models also show an increasing trend with the impact velocity, while retaining the damage characteristics.
-
图 3 RHT本构模型中参数A和N的拟合曲线
Figure 3. Fitting curves on parameters A and N in the RHT constitutive model
图 10 不同状态下不同预应力对白砂岩的冲击损伤
Figure 10. Impact damage of white sandstone in different states with different prestresses
图 14 不同本构模型在不同状态下的应力应变曲线对比
Figure 14. Comparison of stress-strain curves of different constitutive models in different states
图 15 不同本构模型在不同状态下峰值应力变化图
Figure 15. Peak stress variation diagram of different constitutive models in different states
图 16 单轴状态下能量演化时程曲线
Figure 16. Time history curve of energy evolution in uniaxial state
图 19 通过不同本构模型得到的白砂岩试样在0.4 MPa的冲击压力下的应力-应变曲线
Figure 19. Stress-strain curves of white sandstone specimen under the impact pressure of 0.4 MPa obtained by different constitutive models
图 20 试件在0.4 MPa的冲击压力下的冲击损伤
Figure 20. Impact damage of white sandstone specimen under the impact pressure of 0.4 MPa
图 21 不同的本构模型模拟得到的白砂岩石样在0.4 MPa冲击压力下的损伤云图
Figure 21. Damage contours of white sandstone specimens under the impact pressure of 0.4 MPa obtained by different constitutive models
表 1 不同围压下的力学参数
Table 1. Mechanical parameters of white sandstone under different confining pressures
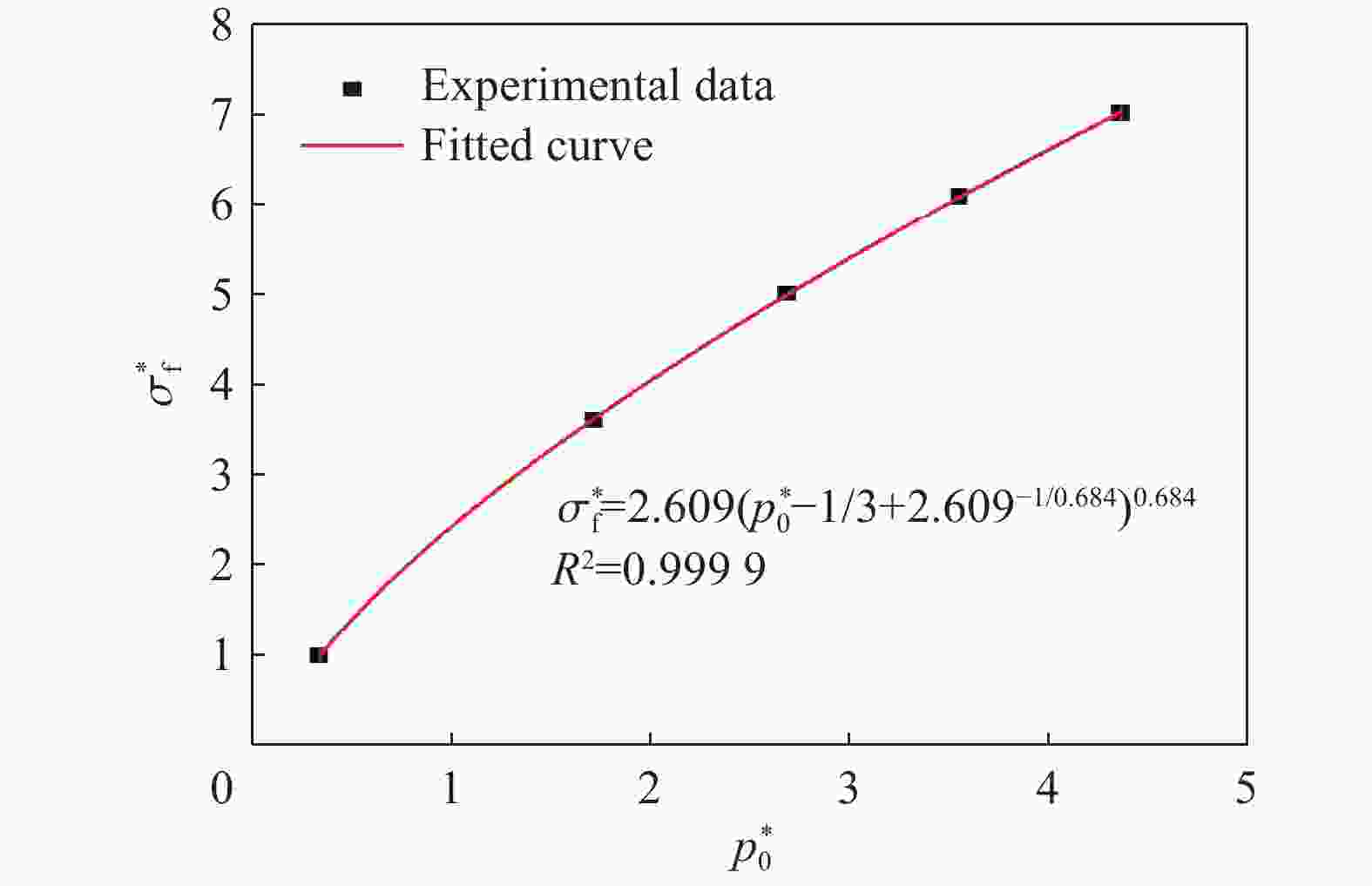
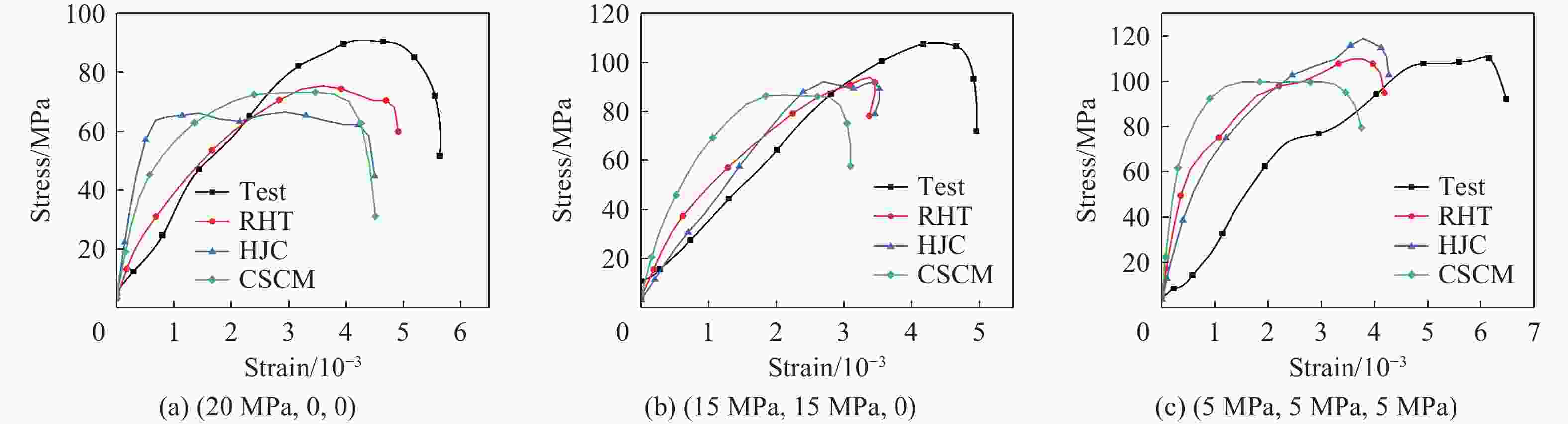
σ2=σ3/MPa σ1/MPa $ {p}_{0}^{*} $ $ {\sigma }_{\mathrm{f}}^{*} $ 0 39.670 0.330 1.000 20 163.580 1.711 3.619 40 239.140 2.682 5.020 60 302.278 3.548 6.107 80 358.819 4.359 7.000 
下载: 导出CSV
表 2 不同围压下的强度
Table 2. Strength at different enclosure pressures
σ2=σ3/MPa σ1/MPa 0 39.67 5 84.59 10 115.33 15 140.92 20 163.58 50 271.76 80 358.82
下载: 导出CSV
表 3 RHT本构模型的参数
Table 3. Parameters of the RHT constitutive model
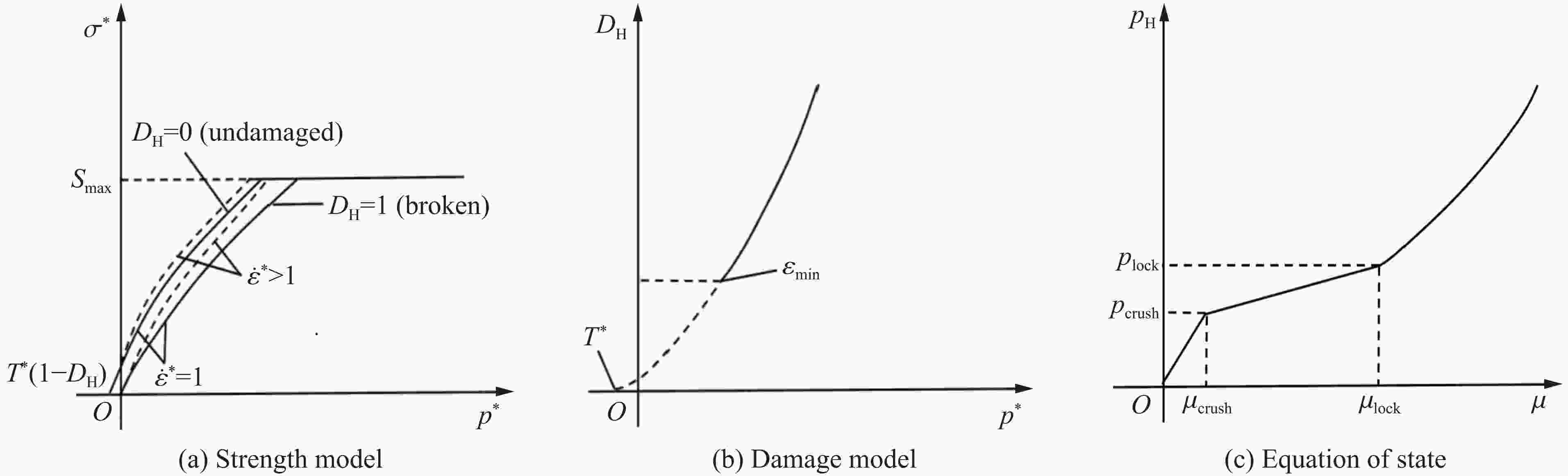
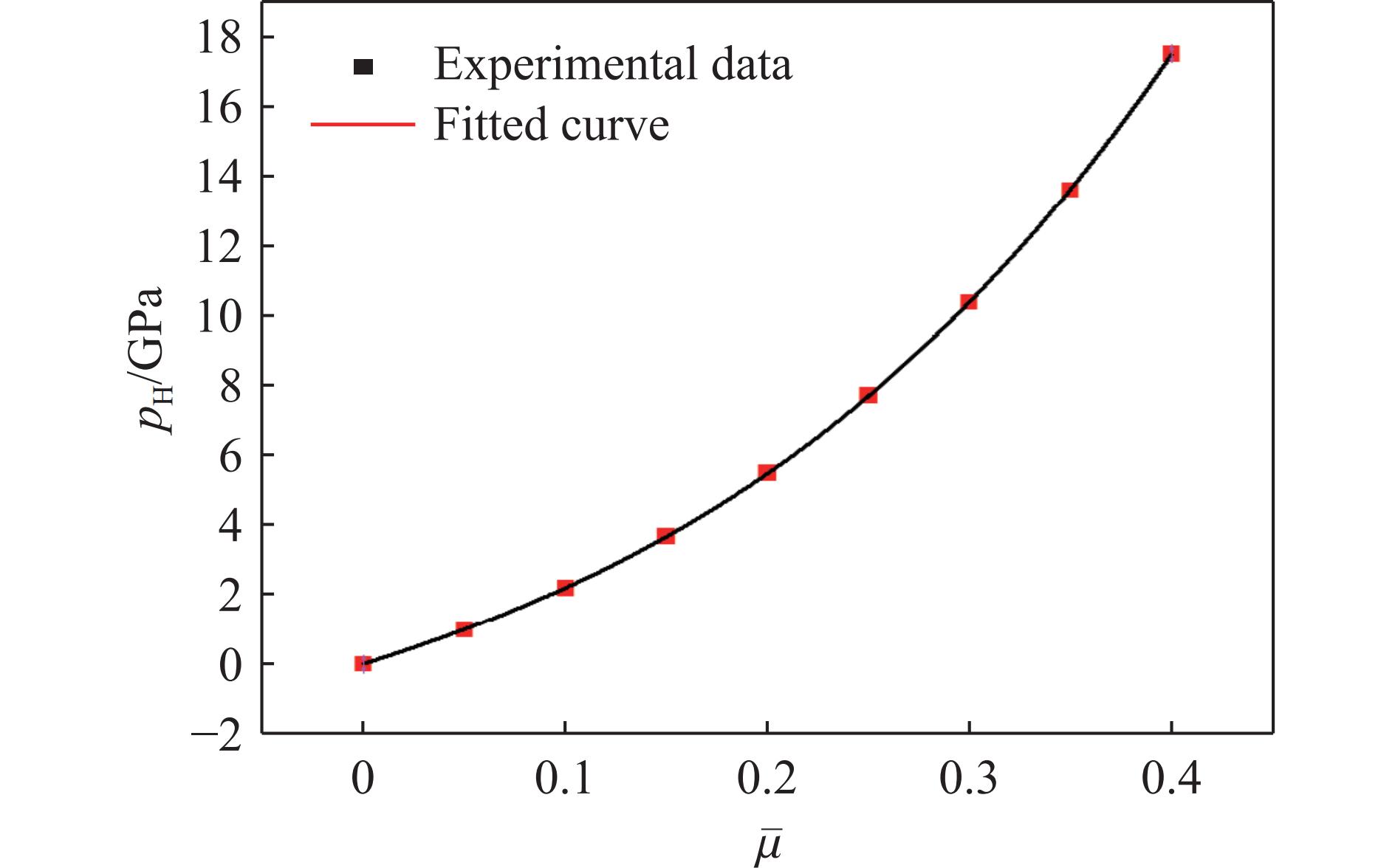
ρ0/(kg·m−3) E/GPa B0 B1 T1/GPa T2/GPa A N 2400 7 0.8 0.8 17.5 0 2.609 0.684 fc/MPa $ f_{\text{s}}^{{*}} $ $f_{\text{t}}^{{*}} $ Q0 B βc βt $ g_{\text{c}}^{*} $ 39.67 0.4 0.1134 0.68 0.05 0.02877 0.01676 0.53 $ g_{\text{t}}^{*} $ A1/GPa A2/GPa A3/GPa pcrush/MPa D1 D2 $ {\varepsilon}_{\text{min}} $ 0.7 17.5 14 −2.974 26.45 0.04 1 0.01
下载: 导出CSV
表 4 HJC本构模型参数
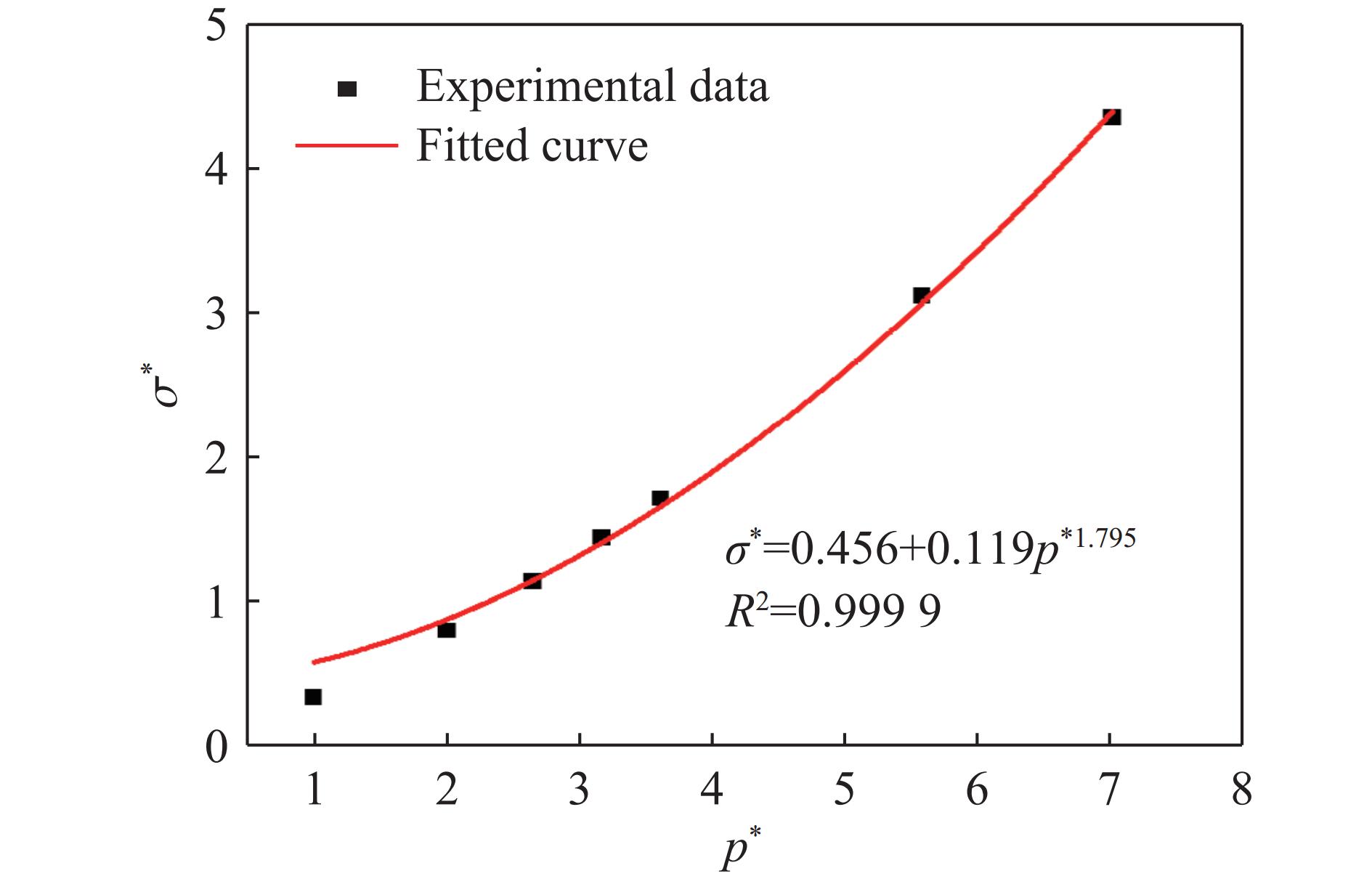
Table 4. Parameters of the HJC constitutive model
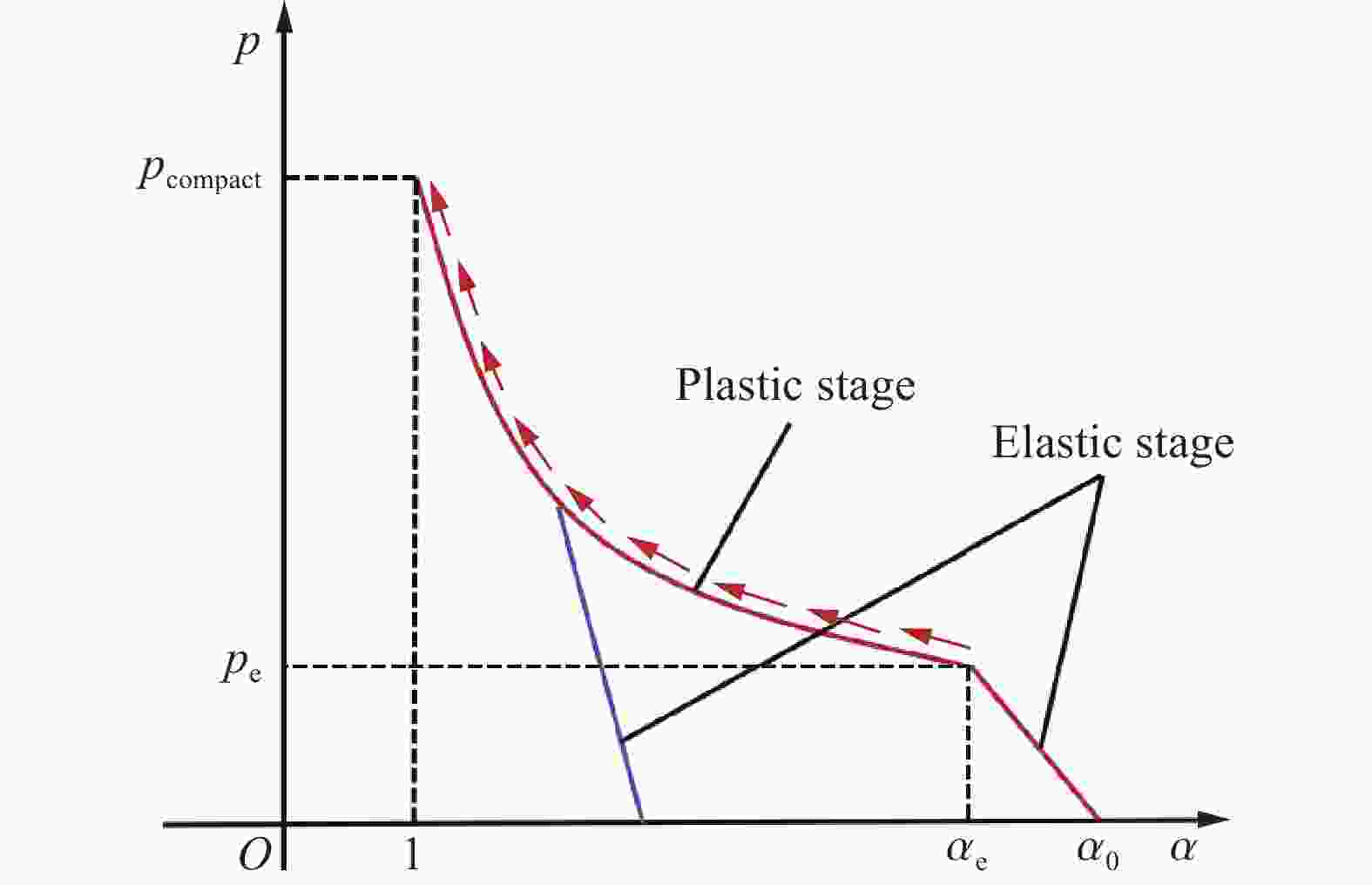
ρ0/(kg·m−3) AH BH CH NH fc/MPa pcrush/MPa 2400 0.456 0.119 0.0173 1.795 39.67 13.22 plock/MPa μcrush μlock D1 D2 Smax $ {\varepsilon}_{\text{min}} $ 810 0.0022 0.0101 0.04 1 7 0.01 T/MPa G/GPa K1/GPa K2/GPa K3/GPa $ {\dot{\varepsilon}}_{\text{0}} $ fs 4.5 2.69 18.56 25.29 94.12 1 0.004
下载: 导出CSV
表 5 CSCM本构模型参数
Table 5. Parameters of the CSCM constitutive model
ρ0/(kg·m−3) fc/MPa 骨粒尺寸/mm 侵蚀系数 2400 39.67 25 1.1
下载: 导出CSV
表 6 单轴状态下不同本构模型能量参数
Table 6. Energy parameters of different constitutive models in uniaxial states
方法 入射能/J 反射能/J 透射能/J 吸收能/J 比吸能/(J·cm−3) 实验 143.128 51.792 54.606 36.730 0.29 RHT本构模型 131.462 41.347 31.613 58.502 0.47 HJC本构模型 131.457 35.718 34.323 61.416 0.49 CSCM本构模型 131.466 34.732 35.753 60.981 0.49
下载: 导出CSV
-
[1] RIEDEL W, KAWAI N, KONDO K I. Numerical assessment for impact strength measurements in concrete materials [J]. International Journal of Impact Engineering, 2009, 36(2): 283–293. DOI: 10.1016/j.ijimpeng.2007.12.012. [2] WU G L, WANG H. Nonlinear correction of elastic section in HJC constitutive model [J]. International Journal of Impact Engineering, 2024, 189: 104955. DOI: 10.1016/j.ijimpeng.2024.104955. [3] LI X H, ZHU Z M, WANG M, et al. Numerical study on the behavior of blasting in deep rock masses [J]. Tunnelling and Underground Space Technology, 2021, 113: 103968. DOI: 10.1016/j.tust.2021.103968. [4] WANG Z L, WANG H C, WANG J G, et al. Finite element analyses of constitutive models performance in the simulation of blast-induced rock cracks [J]. Computers and Geotechnics, 2021, 135: 104172. DOI: 10.1016/j.compgeo.2021.104172. [5] LI X D, LIU K W, SHA Y Y, et al. Experimental and numerical investigation on rock fracturing in tunnel contour blasting under initial stress [J]. International Journal of Impact Engineering, 2024, 185: 104844. DOI: 10.1016/j.ijimpeng.2023.104844. [6] LIU J, ZHANG J C. A modified HJC model for geological materials subjected to blasting loadings [J]. Structures, 2023, 58: 105483. DOI: 10.1016/j.istruc.2023.105483. [7] 宋彦臣, 刘学鹏, 王君杰, 等. 混凝土帽盖模型参数标定及桥梁冲击损伤模拟应用 [J]. 中国公路学报, 2024, 37(5): 151–174. DOI: 10.19721/j.cnki.1001-7372.2024.05.009.SONG Y C, LIU X P, WANG J J, et al. Calibration of parameters for the concrete cap model and its applications in simulating impact-induced damage in bridges [J]. China Journal of Highway and Transport, 2024, 37(5): 151–174. DOI: 10.19721/j.cnki.1001-7372.2024.05.009. [8] YIN X, LI Q H, XU X Y, et al. Investigation of continuous surface cap model (CSCM) for numerical simulation of strain-hardening fibre-reinforced cementitious composites against low-velocity impacts [J]. Composite Structures, 2023, 304: 116424. DOI: 10.1016/j.compstruct.2022.116424. [9] DENG Z, ZHU Z M, ZHOU L, et al. Effect of dynamic loading orientation on fracture properties of surrounding rocks in twin tunnels [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2024, 16(2): 393–409. DOI: 10.1016/j.jrmge.2023.06.017. [10] 匡志平, 袁训康. RHT混凝土本构模型强度参数分析与模拟 [J]. 力学季刊, 2012, 33(1): 158–163. DOI: 10.15959/j.cnki.0254-0053.2012.01.016.KUANG Z P, YUAN X K. The analysis and simulation for the strength parameters of RHT concrete model [J]. Chinese Quarterly of Mechanics, 2012, 33(1): 158–163. DOI: 10.15959/j.cnki.0254-0053.2012.01.016. [11] ZHANG Q B, ZHAO J. A review of dynamic experimental techniques and mechanical behaviour of rock materials [J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1411–1478. DOI: 10.1007/s00603-013-0463-y. [12] XIE L X, LU W B, ZHANG Q B, et al. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses [J]. Tunnelling and Underground Space Technology, 2017, 66: 19–33. DOI: 10.1016/j.tust.2017.03.009. [13] BORRVALL T, RIEDEL W. The RHT concrete model in LS-DYNA [C]//Proceedings of the 8th European LS-DYNA User Conference. Strasbourg, 2011: 23–24. [14] MEYERS M A. Dynamic behavior of materials [M]. New York: John Wiley & Sons, 1994. [15] LSTC. LS-DYNA® keyword user’s manual Volume Ⅱ: material models: LS-DYNA R7.1 [R]. Livermore: LSTC Co. , 2007. [16] HOLMQUIST T J, JOHNSON G R. A computational constitutive model for glass subjected to large strains, high strain rates and high pressures [J]. Journal of Applied Mechanics, 2011, 78(5): 051003. DOI: 10.1115/1.4004326. [17] SCHWER L E, MURRAY Y D. A three‐invariant smooth cap model with mixed hardening [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1994, 18(10): 657–688. DOI: 10.1002/nag.1610181002. [18] MURRAY Y D, LEWIS B A. Numerical simulation of damage in concrete: DNA-TR-94-190 [R]. APTEK, Inc. , Contract DNA, 1995: 1–91. [19] DUVAUT G, LIONS J L. Les inéquations en mécanique et en physique [M]. Paris: Dunod, 1972. [20] YANG J C, LIU K W, LI X D, et al. Stress initialization methods for dynamic numerical simulation of rock mass with high in-situ stress [J]. Journal of Central South University, 2020, 27(10): 3149–3162. DOI: 10.1007/s11771-020-4535-3. [21] 吕绍品, 郑光, 郑宇轩, 等. 静水压下白砂岩的动态力学性能研究 [J]. 硅酸盐通报, 2024, 43(2): 543–554. DOI: 10.16552/j.cnki.issn1001-1625.2024.02.019.LÜ S P, ZHENG G, ZHENG Y X, et al. Dynamic mechanical properties of white sandstone under hydrostatic pressure [J]. Bulletin of the Chinese Ceramic Society, 2024, 43(2): 543–554. DOI: 10.16552/j.cnki.issn1001-1625.2024.02.019. [22] 王礼立. 应力波基础 [M]. 2版. 北京: 国防工业出版社, 2005.WANG L L. Foundation of stress waves [M]. 2nd ed. Beijing: National Defense Industry Press, 2005. [23] LUNDBERG B. A split Hopkinson bar study of energy absorption in dynamic rock fragmentation [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1976, 13(6): 187–197. DOI: 10.1016/0148-9062(76)91285-7. [24] RIEDEL W, THOMA K, HIERMAIER S, et al. Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes [C]//Proceedings of the 9th International Symposium on the Effects of Munitions with Structures. Berlin, 1999: 315–322. [25] 杜闯, 宋帅, 张江鹏. 爆炸冲击作用下三种混凝土本构模型对比研究 [J]. 兵器装备工程学报, 2022, 43(11): 49–56. DOI: 10.11809/bqzbgcxb2022.11.007.DU C, SONG S, ZHANG J P. Comparative study on three concrete constitutive models under blast loading [J]. Journal of Ordnance Equipment Engineering, 2022, 43(11): 49–56. DOI: 10.11809/bqzbgcxb2022.11.007. [26] WANG Z L, NI Y, WANG J G, et al. Improvement and performance analysis of constitutive model for rock blasting damage simulation [J]. Simulation Modelling Practice and Theory, 2025, 138: 103043. DOI: 10.1016/j.simpat.2024.103043. -
计量
- 文章访问数: 236
- HTML全文浏览量: 25
- PDF下载量: 90
- 被引次数: 0