Cross-scale approach for impact damage and fatigue based on the strain gradient theory
-
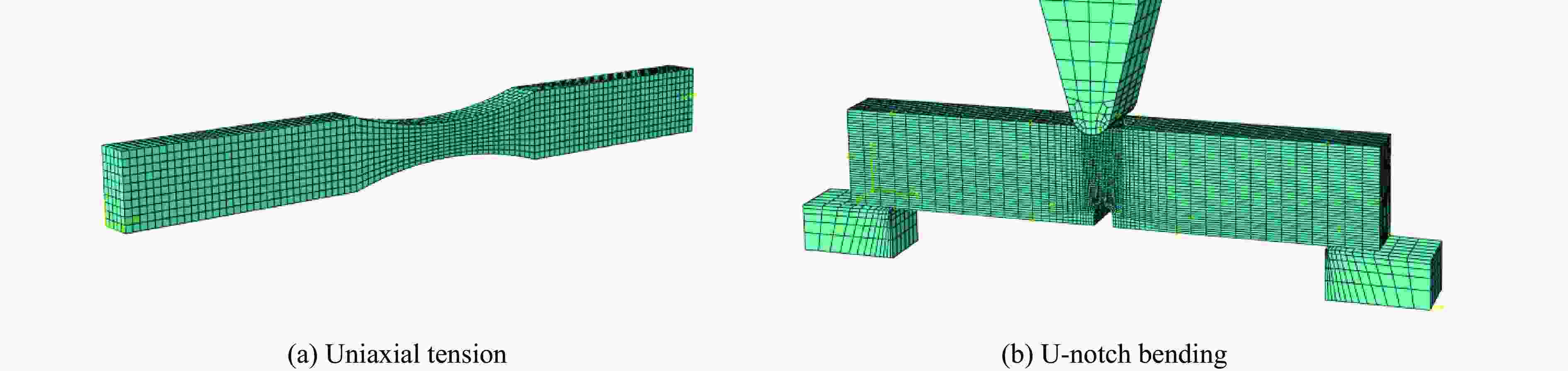
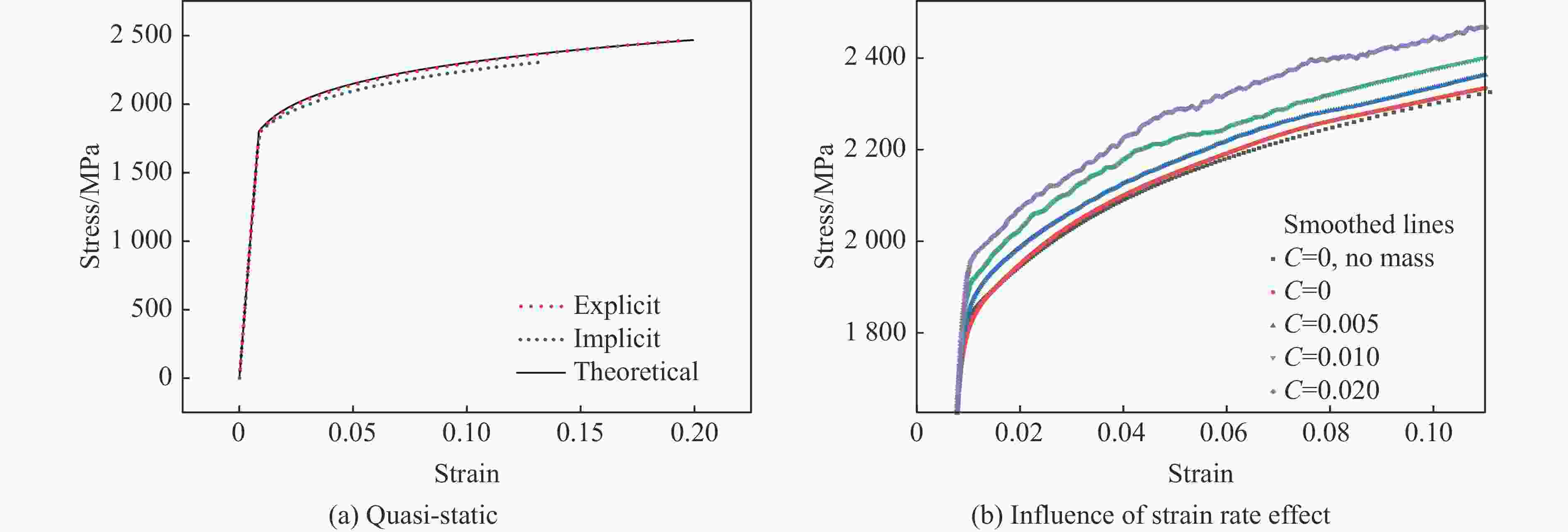
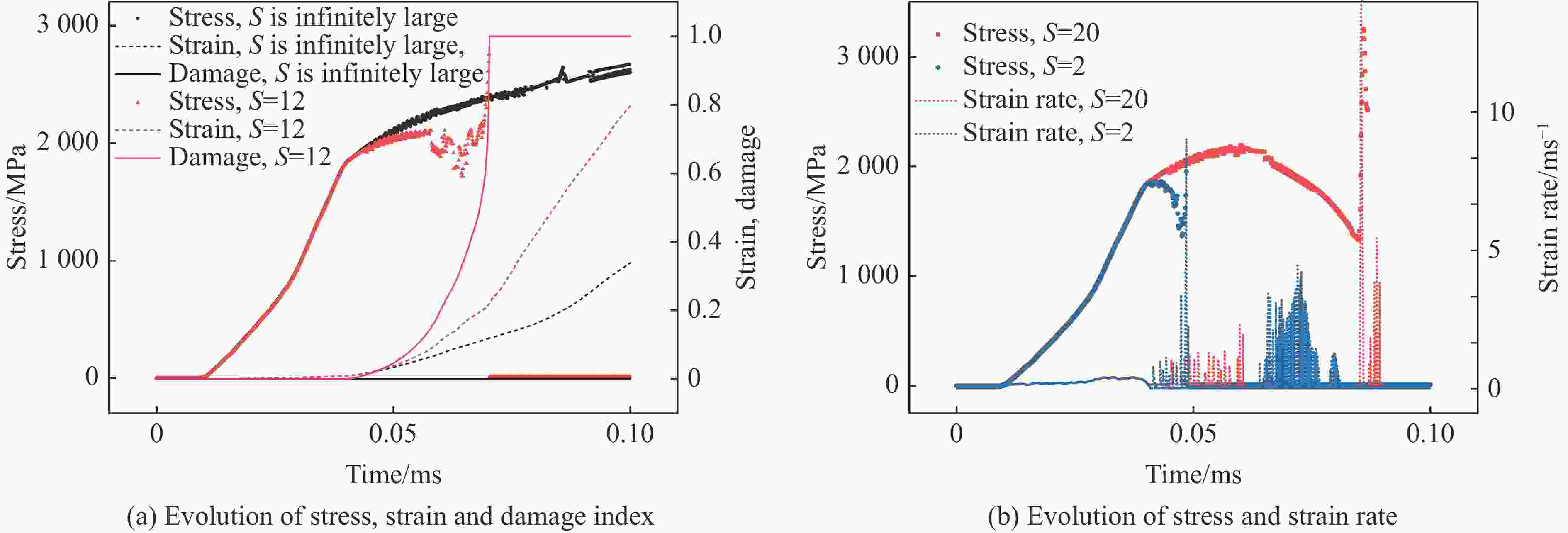
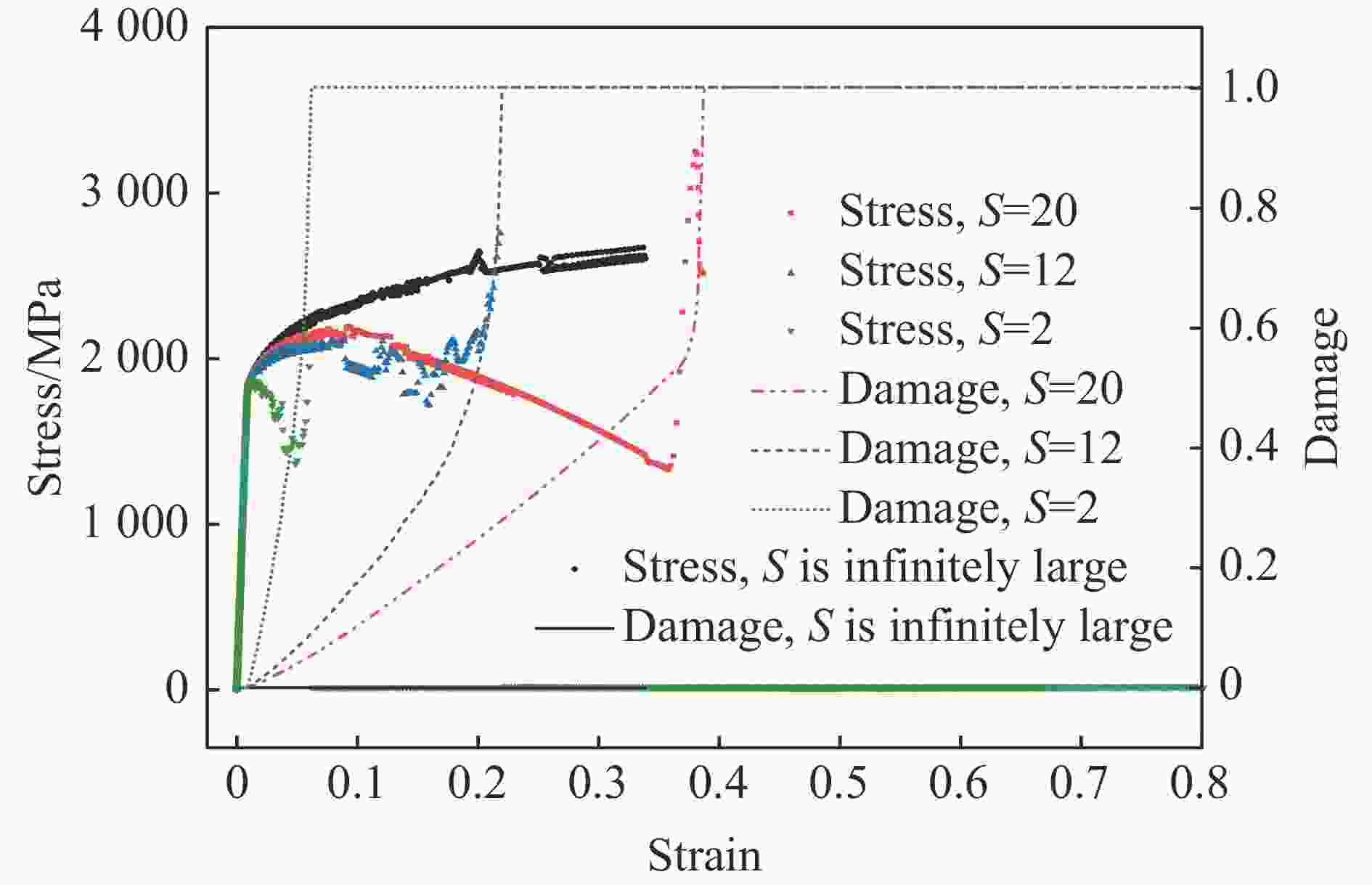
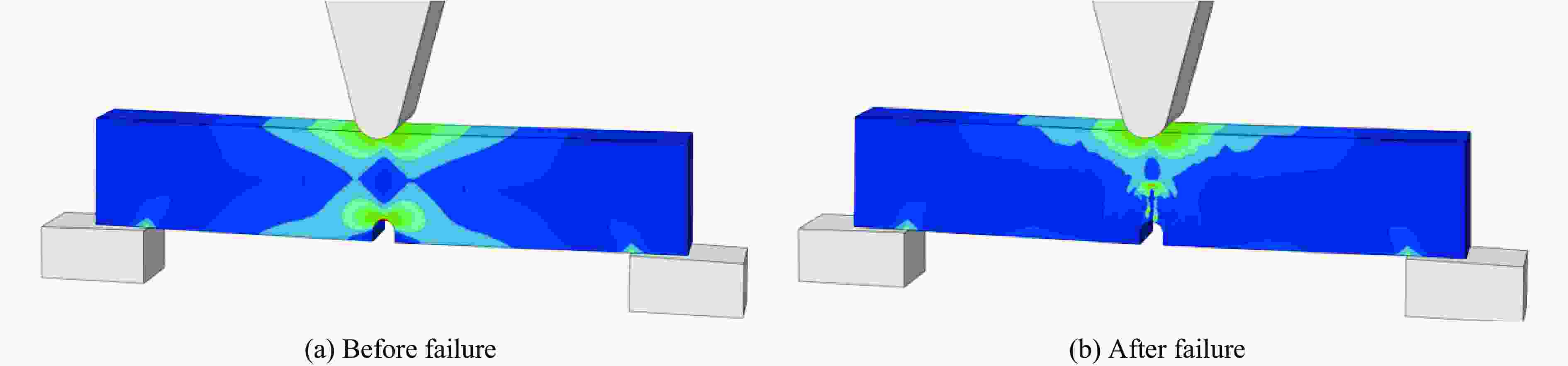
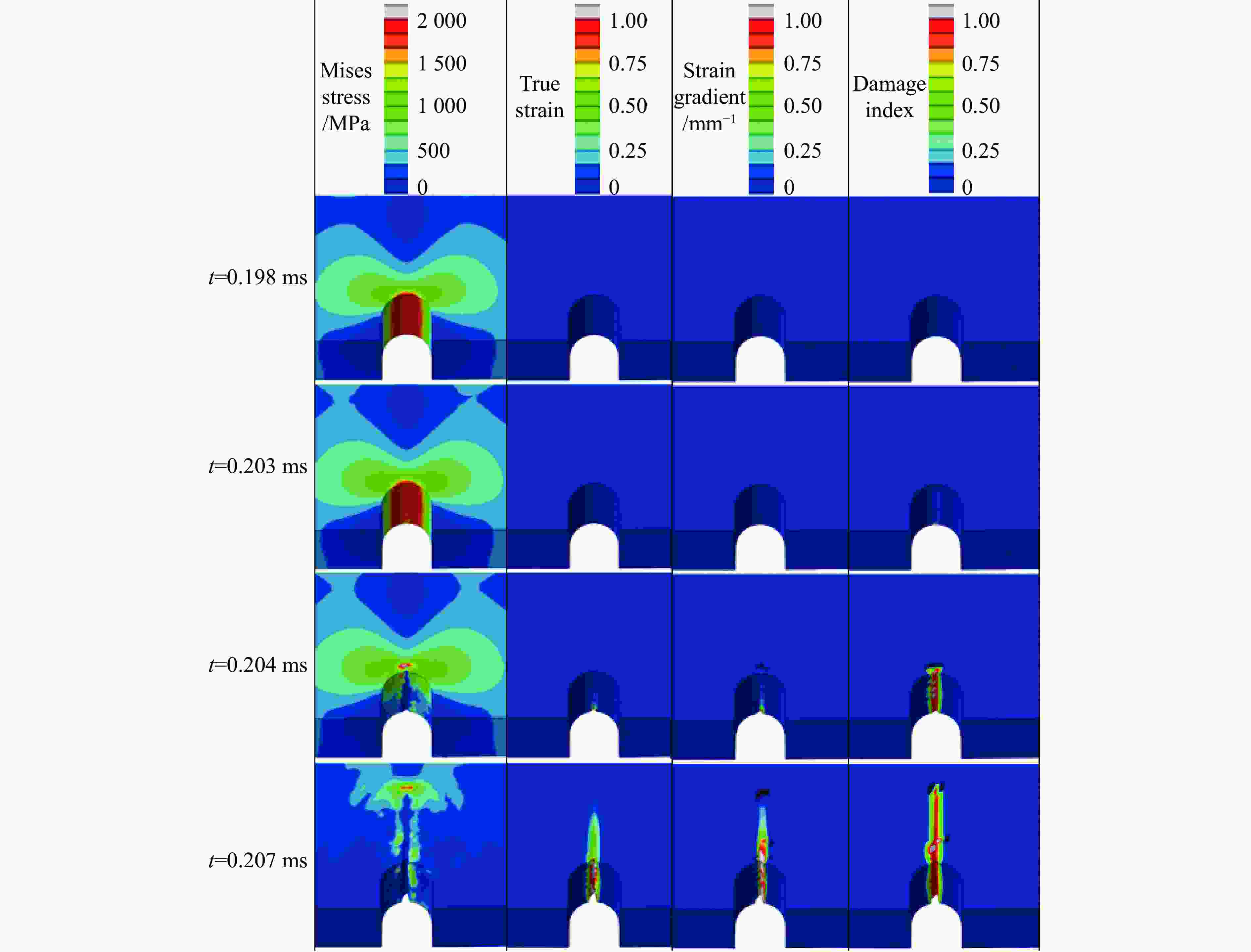
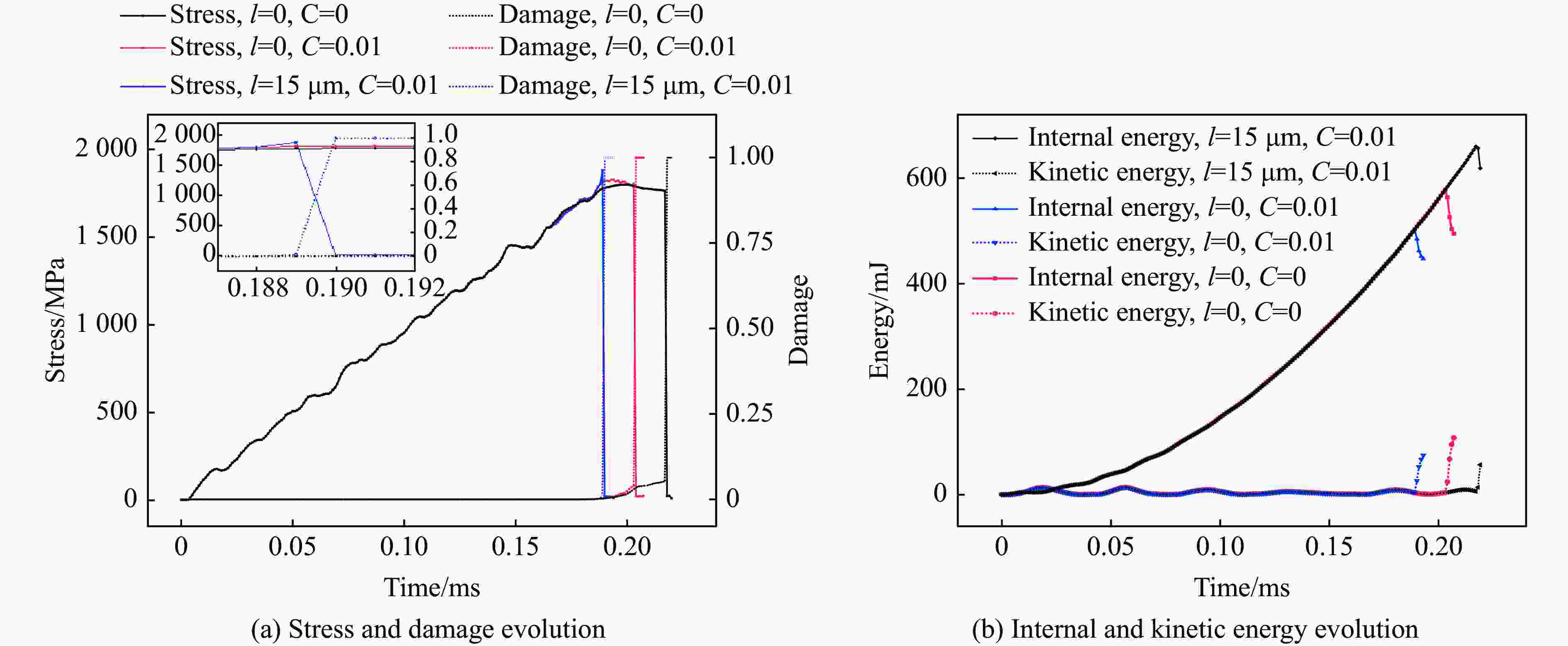
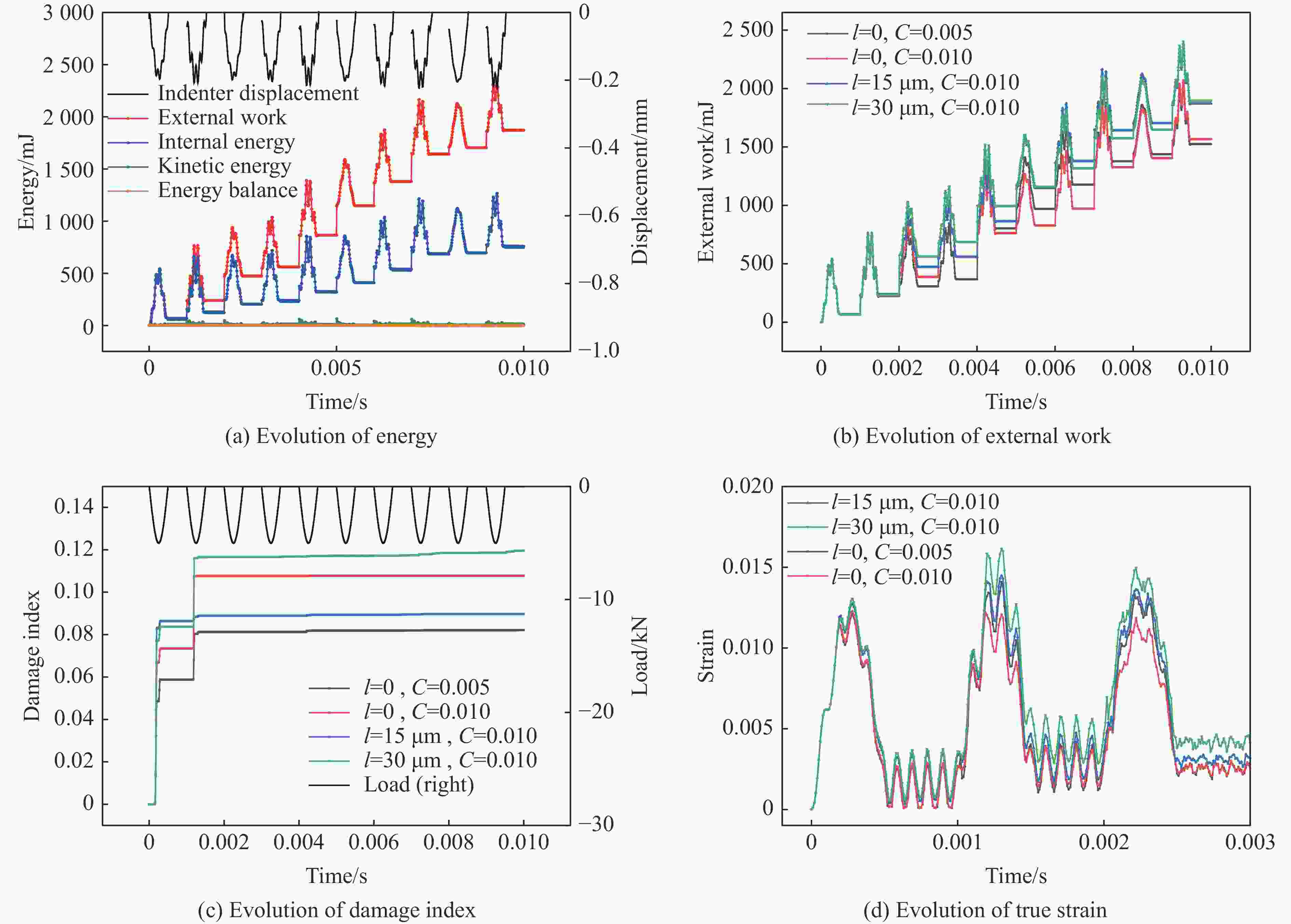
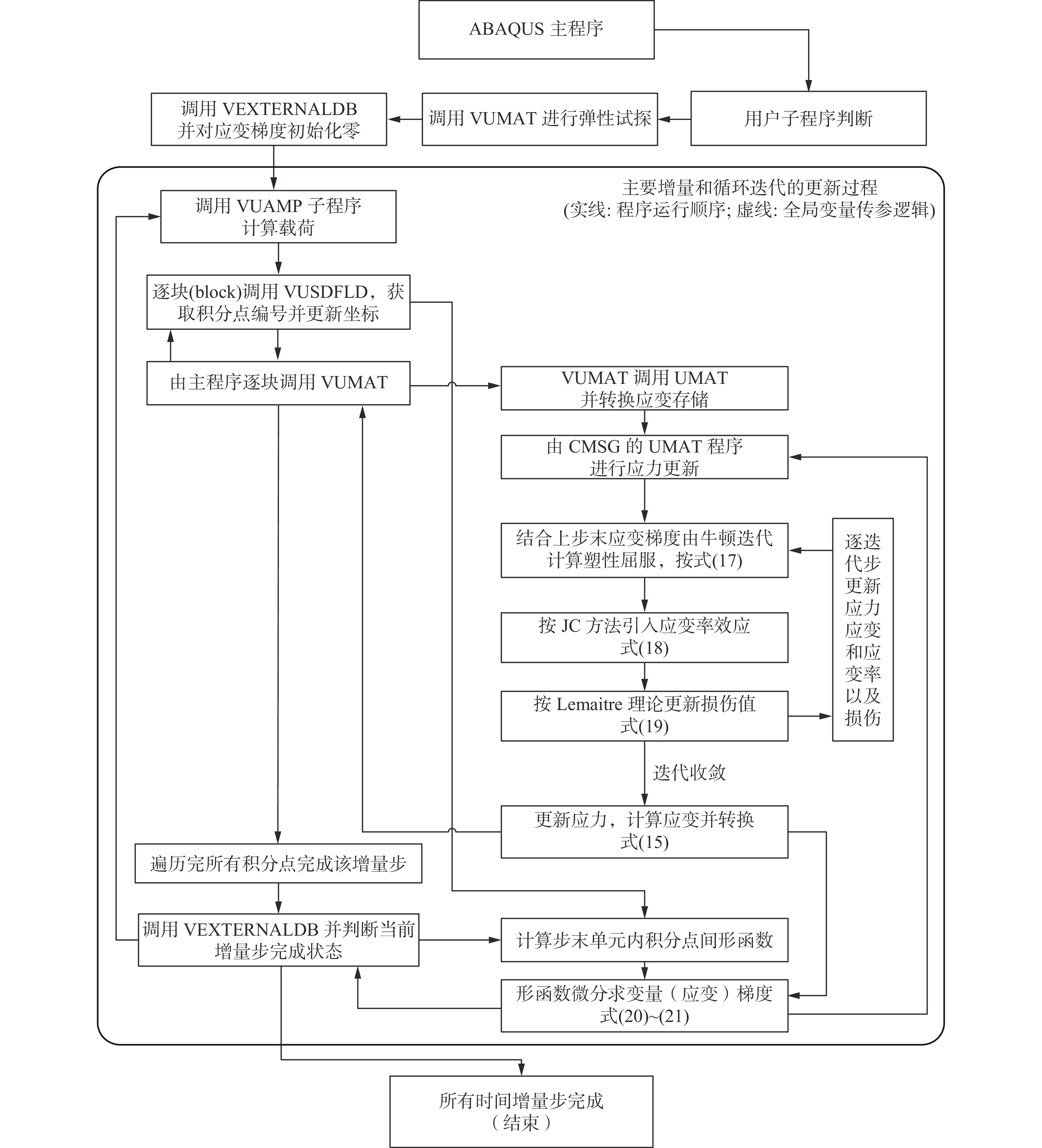
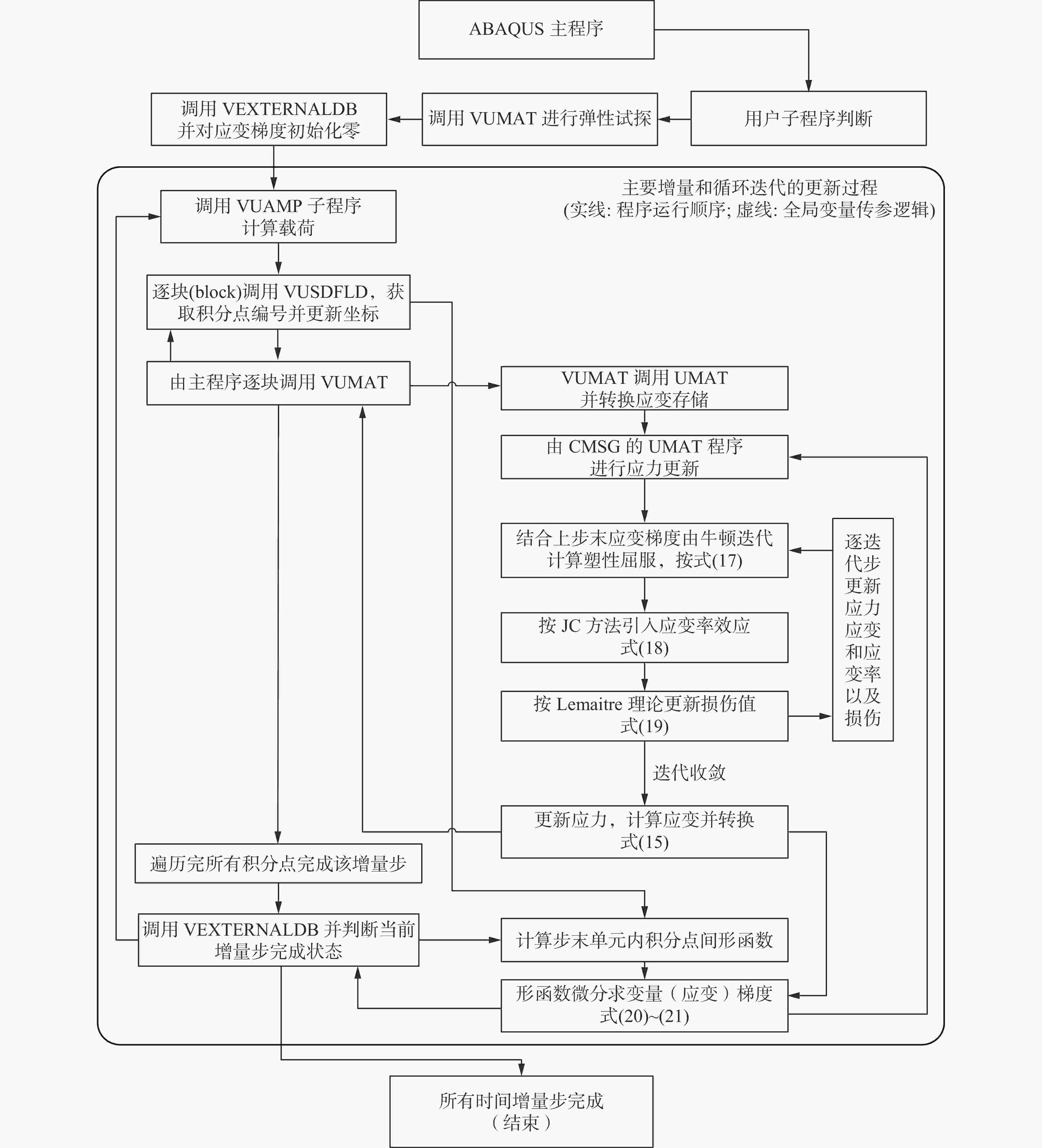
摘要: 为兼顾考虑材料尺度效应和建模预测效率的冲击损伤和冲击疲劳研究方法，立足冲击损伤和疲劳过程中的金属塑性变形机理，研究了冲击损伤过程中尺度效应影响下的材料构效行为，建立了金属材料的去局域化、跨尺度冲击损伤本构理论，形成了面向先进制造多尺度金属材料的冲击损伤和疲劳的仿真方法。该方法利用低阶应变梯度理论实现尺度效应描述，在Johnson-Cook冲击动力学模型和Lemaitre冲击损伤模型的基础上，实现了跨尺度冲击动力学及损伤演化的描述，并可以在VUMAT子程序中便捷地实现该本构的有限元计算。有限元结果表明，材料的不均匀变形带来了较高的应变梯度，使得材料的应力水平在加工硬化及应变率硬化效应上进一步提升，同时也让材料更快地进入损伤阶段，导致承载力降低或提前失效，这与金属材料在强度与韧性间的拮抗关系保持了一致。Abstract: Impact damage and fatigue are emerging challenges in the defense industry and civil infrastructure. The more pronounced material size effect induced by advanced manufacturing processes makes mechanical analysis and life prediction in these contexts more complex. Currently, there is no convenient and effective method for predicting and designing the cross-scale impact damage and fatigue performance of metal materials. This research is based on the metallic plasticity mechanisms in the impact damage and fatigue processes, investigating the material performance under the influence of the material size effect during the impact damage process. A non-local, cross-scale impact and damage constitutive theory for metallic materials was developed, and an impact damage and fatigue simulation method for advanced manufactured metals was established. This method used the conventional theory of mechanism-based strain gradient (CMSG) to describe the size effect and was built on the Johnson-Cook impact dynamics model and Lemaitre impact damage model to describe cross-scale impact dynamics and damage evolution. This approach could be conveniently implemented in finite element analysis with the VUMAT and relevant subroutines. The present work established uniaxial and U-notch bending finite element models and verified the influence of work hardening, strain rate hardening, size effect, and damage effect on static and impact dynamic response of metals. Simulation results indicated the material behavior corresponds to the material characteristic and constitutive design. The distribution and evolution of the stress, strain, strain gradient, and damage before and after material failure are also discussed. The results show that the inhomogeneous deformation caused by advanced manufacturing processes leads to higher strain gradients, which further increase the flow stress through work hardening and strain rate hardening effects and strengthen the material. However, this also causes the material to enter the damage stage earlier, leading to reduced impact and fatigue-bearing capacity or premature failure. These findings are consistent with the inherent trade-off between strength and toughness of metallic materials.
-
Key words:
- impact damage /
- impact fatigue /
- cross-scale mechanics /
- strain gradient plasticity
-
图 1 本构有限元实现的程序流程框图
Figure 1. Diagram of the finite element implementation of the present constitutive relation
图 2 单轴拉伸和三点弯曲试样的有限元建模
Figure 2. Finite element modeling of uniaxial tension and U-notch bending specimens
图 3 单轴准静态和冲击载荷下的整体应力-应变关系
Figure 3. Comparison of stress-strain curves under uniaxial tension
图 4 在率效应和损伤效应作用下应力、应变、损伤和应变率的演化
Figure 4. Evolution of stress, strain, damage index, and strain rate under rate and damage effects
图 5 不同损伤参数对材料在冲击过程中的应力应变关系的影响
Figure 5. Inference of different damage parameters on the stress-strain relationship of material during impact
图 6 U缺口试样在冲击损伤破坏前后的整体应力分布
Figure 6. Stress distribution of the U-notch sample before and after impact damage and failure
图 7 损伤关键时刻的应力、应变、应变梯度及损伤度的演化过程
Figure 7. Evolution of stress, strain, strain gradient, and damage index at the moment of failure
图 8 单次大载荷冲击作用对尺度效应与应变率效应的影响
Figure 8. Stress, damage, and energy evolution under the impact of a large load with and without considering strain rate and strain gradient effects
图 9 多次较小载荷冲击作用下整体能量演化和局部应力应变等力学响应的演化过程
Figure 9. Evolution of energy and local mechanical response during multiple impacts
图 10 多次小载荷冲击作用对系统能量及损伤、应变演化及尺度效应、率效应的影响
Figure 10. Evolution of energy, damage, and strain during multiple impacts and influence of strain rate and strain gradient effects
表 1 有限元仿真采用的本构参数
Table 1. Constitutive parameters used in the finite element simulation
杨氏模量E/GPa 泊松比ν 屈服强度Y/MPa 幂硬化系数n 黏塑性参数m 材料特征长度l/μm 率硬化参数C 损伤参数S/MPa 损伤参数mD 210 0.3 1800 0.1 20 15 0.017 12 10.1 
下载: 导出CSV
-
[1] WANG B W, QIAN C C, BAI C Y, et al. Study on impact fatigue test and life prediction method of TC18 titanium alloy [J]. International Journal of Fatigue, 2023, 168: 107391. DOI: 10.1016/j.ijfatigue.2022.107391. [2] 於之杰, 郭玉佩, 孙汉斌, 等. 先进材料及工艺的结构完整性研究进展 [J]. 航空学报, 2024, 45(18): 029888. DOI: 10.7527/S1000-6893.2024.29888.YU Z J, GUO Y P, SUN H B, et al. Recent progress in structural integrity of novel materials and advanced techniques [J]. Acta Aeronautica et Astronautica Sinica, 2024, 45(18): 029888. DOI: 10.7527/S1000-6893.2024.29888. [3] SYED A K, PLASKITT R, HILL M, et al. Strain controlled fatigue behaviour of a wire + arc additive manufactured Ti-6Al-4V [J]. International Journal of Fatigue, 2023, 171: 107579. DOI: 10.1016/j.ijfatigue.2023.107579. [4] YADOLLAHI A, SHAMSAEI N. Additive manufacturing of fatigue resistant materials: challenges and opportunities [J]. International Journal of Fatigue, 2017, 98: 14–31. DOI: 10.1016/j.ijfatigue.2017.01.001. [5] 王彬文, 陈先民, 苏运来, 等. 中国航空工业疲劳与结构完整性研究进展与展望 [J]. 航空学报, 2021, 42(5): 524651. DOI: 10.7527/S1000-6893.2020.24651.WANG B W, CHEN X M, SU Y L, et al. Research progress and prospect of fatigue and structural integrity for aeronautical industry in China [J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(5): 524651. DOI: 10.7527/S1000-6893.2020.24651. [6] AI Y, ZHU S P, LIAO D, et al. Probabilistic modeling of fatigue life distribution and size effect of components with random defects [J]. International Journal of Fatigue, 2019, 126: 165–173. DOI: 10.1016/j.ijfatigue.2019.05.005. [7] GAO H, HUANG Y, NIX W D, et al. Mechanism-based strain gradient plasticity—I. theory [J]. Journal of the Mechanics and Physics of Solids, 1999, 47(6): 1239–1263. DOI: 10.1016/S0022-5096(98)00103-3. [8] 陈泽坤, 蒋佳希, 王宇嘉, 等. 金属增材制造中的缺陷、组织形貌和成形材料力学性能 [J]. 力学学报, 2021, 53(12): 3190–3205. DOI: 10.6052/0459-1879-21-472.CHEN Z K, JIANG J X, WANG Y J, et al. Defects, microstructures and mechanical properties of materials fabricated by metal additive manufacturing [J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(12): 3190–3205. DOI: 10.6052/0459-1879-21-472. [9] ZHANG X, ZHAO J F, KANG G Z, et al. Geometrically necessary dislocations and related kinematic hardening in gradient grained materials: A nonlocal crystal plasticity study [J]. International Journal of Plasticity, 2023, 163: 103553. DOI: 10.1016/j.ijplas.2023.103553. [10] FOREST S. Micromorphic approach for gradient elasticity, viscoplasticity, and damage [J]. Journal of Engineering Mechanics, 2009, 135(3): 117–131. DOI: 10.1061/(ASCE)0733-9399(2009)135:3(117). [11] WANG Y F, ZHU Y T, YU Z J, et al. Hetero-zone boundary affected region: a primary microstructural factor controlling extra work hardening in heterostructure [J]. Acta Materialia, 2022, 241: 118395. DOI: 10.1016/j.actamat.2022.118395. [12] MADEJSKI B, MALICKI M, CZARNEWICZ S, et al. Microstructural and mechanical properties of selective laser melted Inconel 718 for different specimen sizes [J]. Fatigue of Aircraft Structures, 2020, 2020(12): 15–26. DOI: 10.2478/fas-2020-0002. [13] LIAO D, ZHU S P, KESHTEGAR B, et al. Probabilistic framework for fatigue life assessment of notched components under size effects [J]. International Journal of Mechanical Sciences, 2020, 181: 105685. DOI: 10.1016/j.ijmecsci.2020.105685. [14] TOMASZEWSKI T. Modelling of critical defect distributions for estimating the size effect of selective laser melted 316L stainless steel [J]. International Journal of Fatigue, 2023, 167: 107378. DOI: 10.1016/j.ijfatigue.2022.107378. [15] 李泊立, 赵思晗, 刘圆梦, 等. Hopkinson杆式冲击疲劳试验方法研究 [J]. 振动与冲击, 2023, 42(2): 132–138. DOI: 10.13465/j.cnki.jvs.2023.02.016.LI B L, ZHAO S H, LIU Y M, et al. Method for experiment study on impact fatigue based on Hopkinson bar [J]. Journal of Vibration and Shock, 2023, 42(2): 132–138. DOI: 10.13465/j.cnki.jvs.2023.02.016. [16] LIU W B, CHENG Y Y, SUI H N, et al. Microstructure-based intergranular fatigue crack nucleation model: dislocation transmission versus grain boundary cracking [J]. Journal of the Mechanics and Physics of Solids, 2023, 173: 105233. DOI: 10.1016/j.jmps.2023.105233. [17] FLECK N A, MULLER G M, ASHBY M F, et al. Strain gradient plasticity: theory and experiment [J]. Acta Metallurgica et Materialia, 1994, 42(2): 475–487. DOI: 10.1016/0956-7151(94)90502-9. [18] HUANG Y, QU S, HWANG K C, et al. A conventional theory of mechanism-based strain gradient plasticity [J]. International Journal of Plasticity, 2004, 20(4/5): 753–782. DOI: 10.1016/j.ijplas.2003.08.002. [19] 於之杰, 魏悦广. 固体跨尺度压痕标度律的研究与展望 [J]. 力学学报, 2022, 54(8): 2085–2100. DOI: 10.6052/0459-1879-22-273.YU Z J, WEI Y G. Review on the researches and prospect of the trans-scale indentation scaling law of solids [J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(8): 2085–2100. DOI: 10.6052/0459-1879-22-273. [20] YU Z J, LIN Z Y, WEI Y G. Closed-form functions of cross-scale indentation scaling relationships based on a strain gradient plasticity theory [J]. Philosophical Magazine, 2021, 101(11): 1305–1326. DOI: 10.1080/14786435.2021.1897896. [21] YU Z J, WEI Y G. A study of indentation scaling relationships of elastic-perfectly plastic solids with an inclusion near the conical indenter tip [J]. Science China Technological Sciences, 2019, 62(5): 721–728. DOI: 10.1007/s11431-018-9424-4. [22] YU Z J, LIN Z Y, WEI Y G. Investigation on cross-scale indentation scaling relationships of elastic–plastic solids [J]. Acta Mechanica, 2021, 232(4): 1479–1496. DOI: 10.1007/s00707-020-02913-2. [23] 邱吉, 苏步云, 金涛, 等. 高温下多主元合金的动态变形行为与本构建模 [J]. 爆炸与冲击, 2024, 44(7): 071001. DOI: 10.11883/bzycj-2023-0439.QIU J, SU B Y, JIN T, et al. Dynamic deformation behavior and constitutive modeling of multi-component alloys at high temperature [J]. Explosion and Shock Waves, 2024, 44(7): 071001. DOI: 10.11883/bzycj-2023-0439. [24] GOPINATH K, NARAYANAMURTHY V, KHADERI S N, et al. Determination of parameters for Johnson-cook dynamic constitutive and damage models for E250 structural steel and experimental validations [J]. Journal of Materials Engineering and Performance, 2024, 33(20): 10940–10960. DOI: 10.1007/s11665-023-08733-4. [25] LEMAITRE J. A continuous damage mechanics model for ductile fracture [J]. Journal of Engineering Materials and Technology, 1985, 107(1): 83–89. DOI: 10.1115/1.3225775. [26] TAYLOR G I. The mechanism of plastic deformation of crystals. part I—theoretical [J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1934, 145(855): 362–387. DOI: 10.1098/rspa.1934.0106. [27] TAYLOR G I. Plastic strain in metals [J]. J. Inst. Metals, 1938, 62: 307–324. [28] FLECK N A, HUTCHINSON J W. Strain gradient plasticity [J]. Advances in Applied Mechanics, 1997, 33: 295–361. DOI: 10.1016/S0065-2156(08)70388-0. [29] KOK S, BEAUDOIN A J, TORTORELLI D A. A polycrystal plasticity model based on the mechanical threshold [J]. International Journal of Plasticity, 2002, 18(5/6): 715–741. DOI: 10.1016/S0749-6419(01)00051-1. [30] 郭玉佩, 王彬文, 刘小川, 等. TC18钛合金多次冲击损伤演化规律 [J]. 科学技术与工程, 2021, 21(24): 10518–10524. DOI: 10.3969/j.issn.1671-1815.2021.24.057.GUO Y P, WANG B W, LIU X C, et al. Damage evolution law of TC18 titanium alloy under repeated impact loading [J]. Science Technology and Engineering, 2021, 21(24): 10518–10524. DOI: 10.3969/j.issn.1671-1815.2021.24.057. [31] ZHAO J F, LU X C, LIU J L, et al. The tension-compression behavior of gradient structured materials: a deformation-mechanism-based strain gradient plasticity model [J]. Mechanics of Materials, 2021, 159: 103912. DOI: 10.1016/j.mechmat.2021.103912. -
计量
- 文章访问数: 119
- HTML全文浏览量: 3
- PDF下载量: 26
- 被引次数: 0