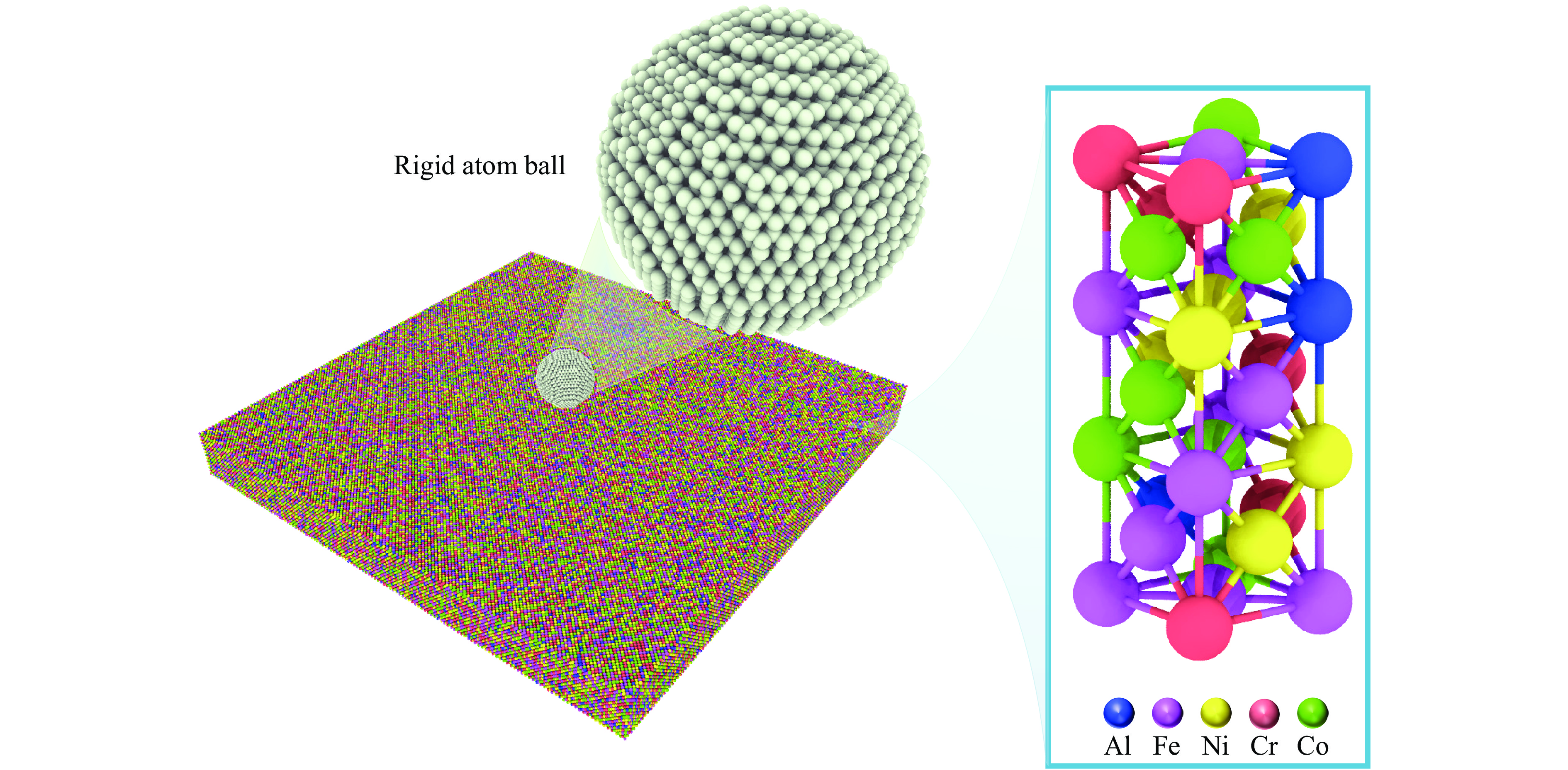
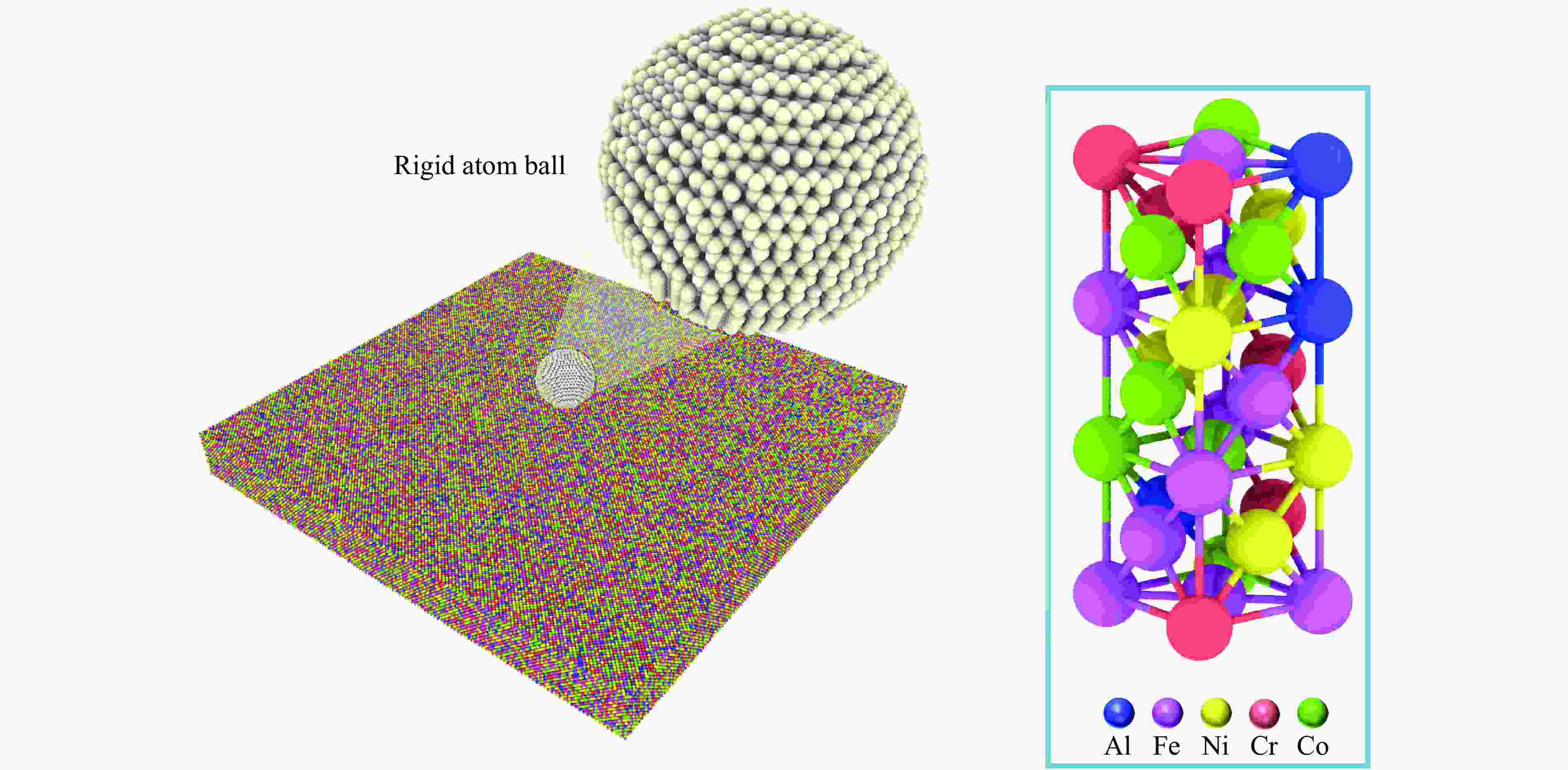
Dynamic response mechanism and cumulative damage effect of Al0.3CoCrFeNi high entropy alloy under repeated impact loading
-
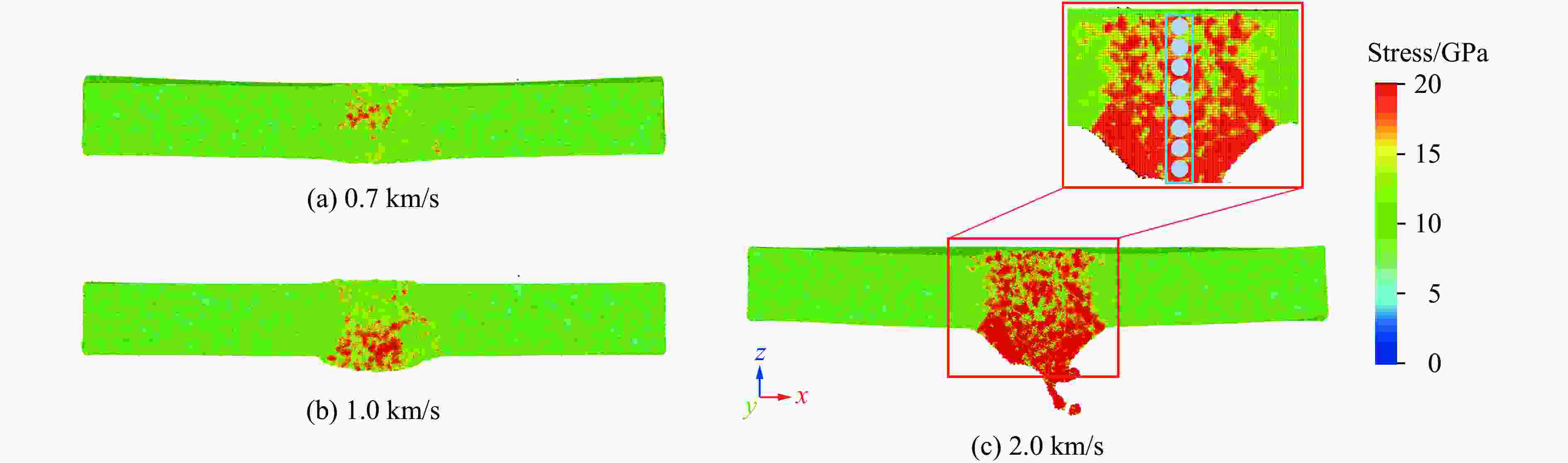
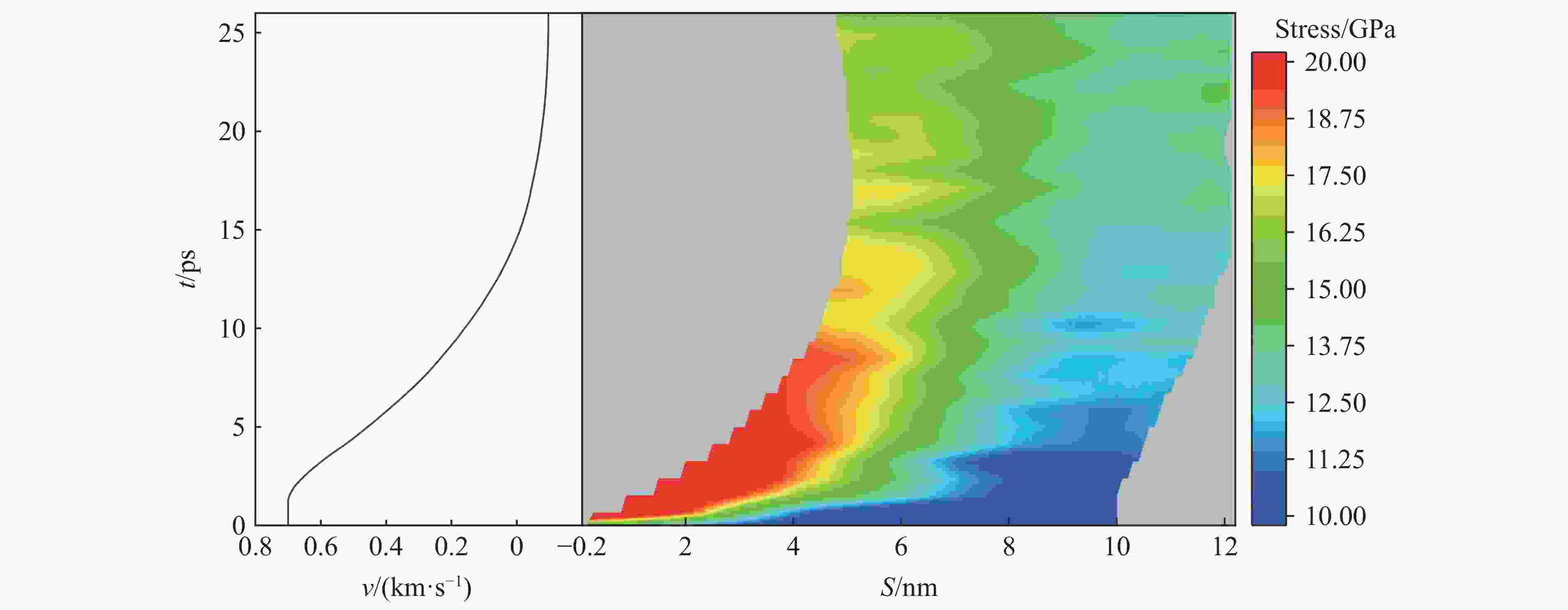
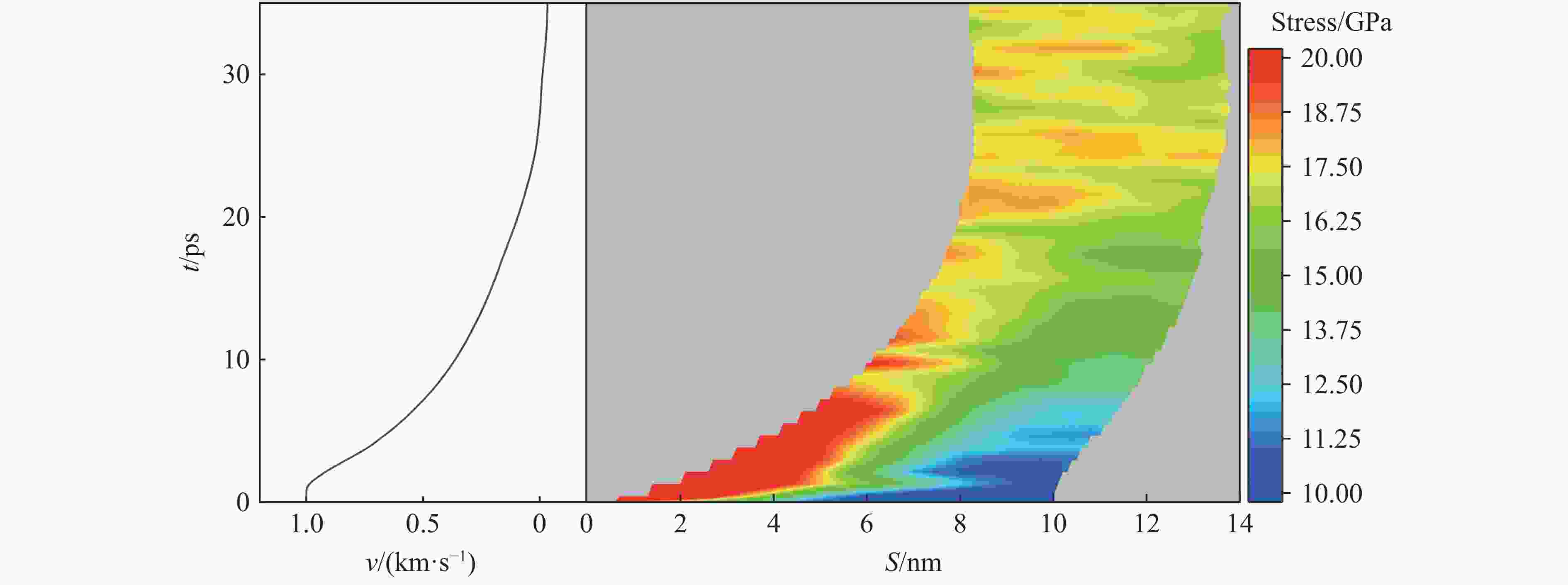
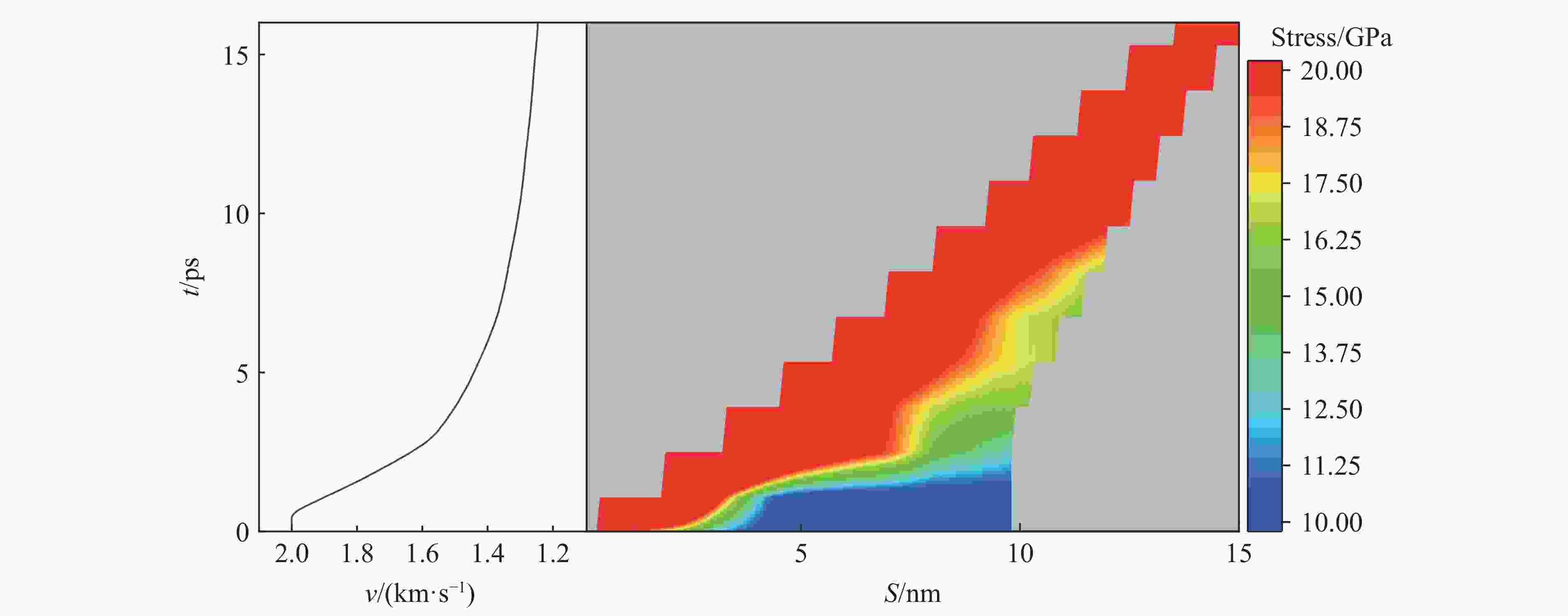
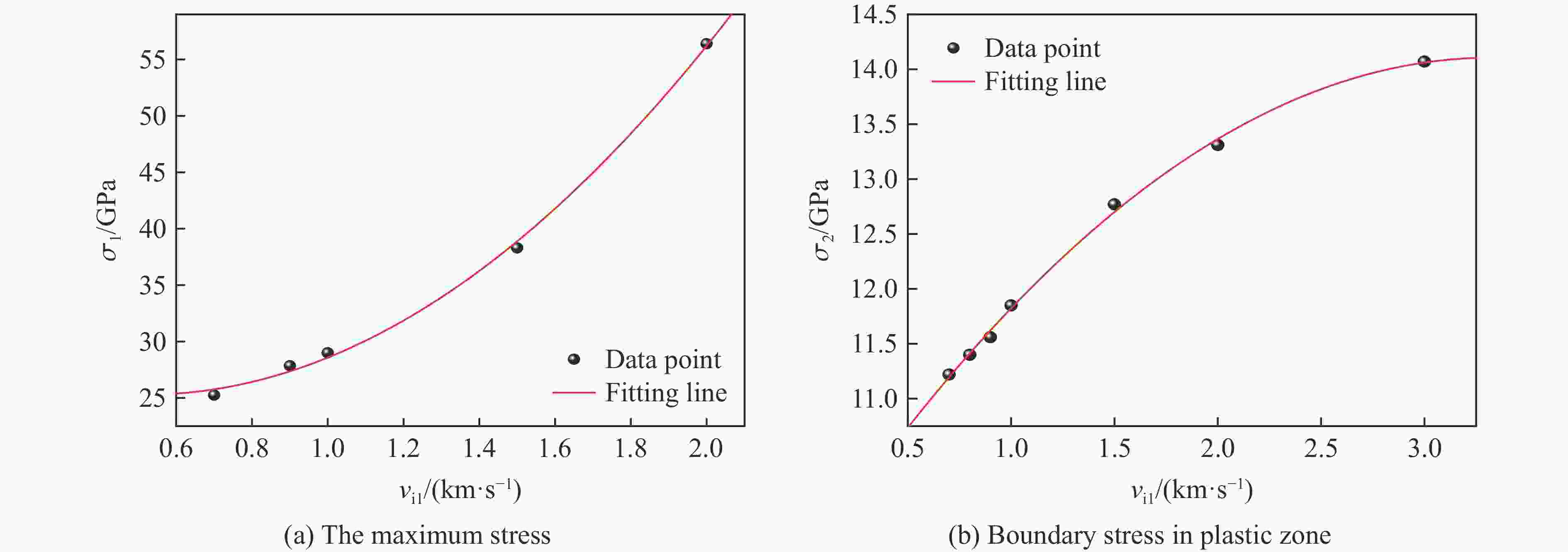
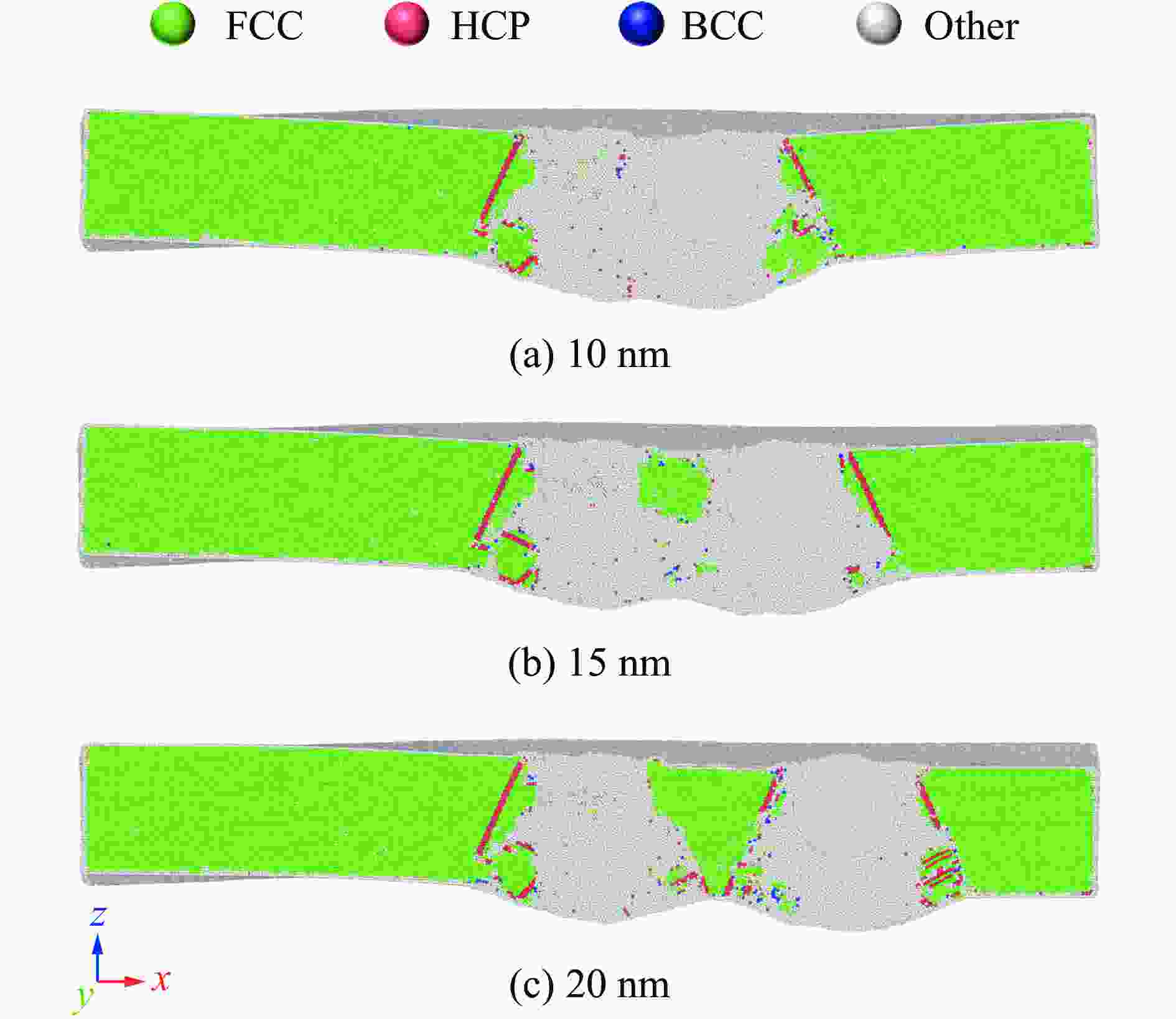
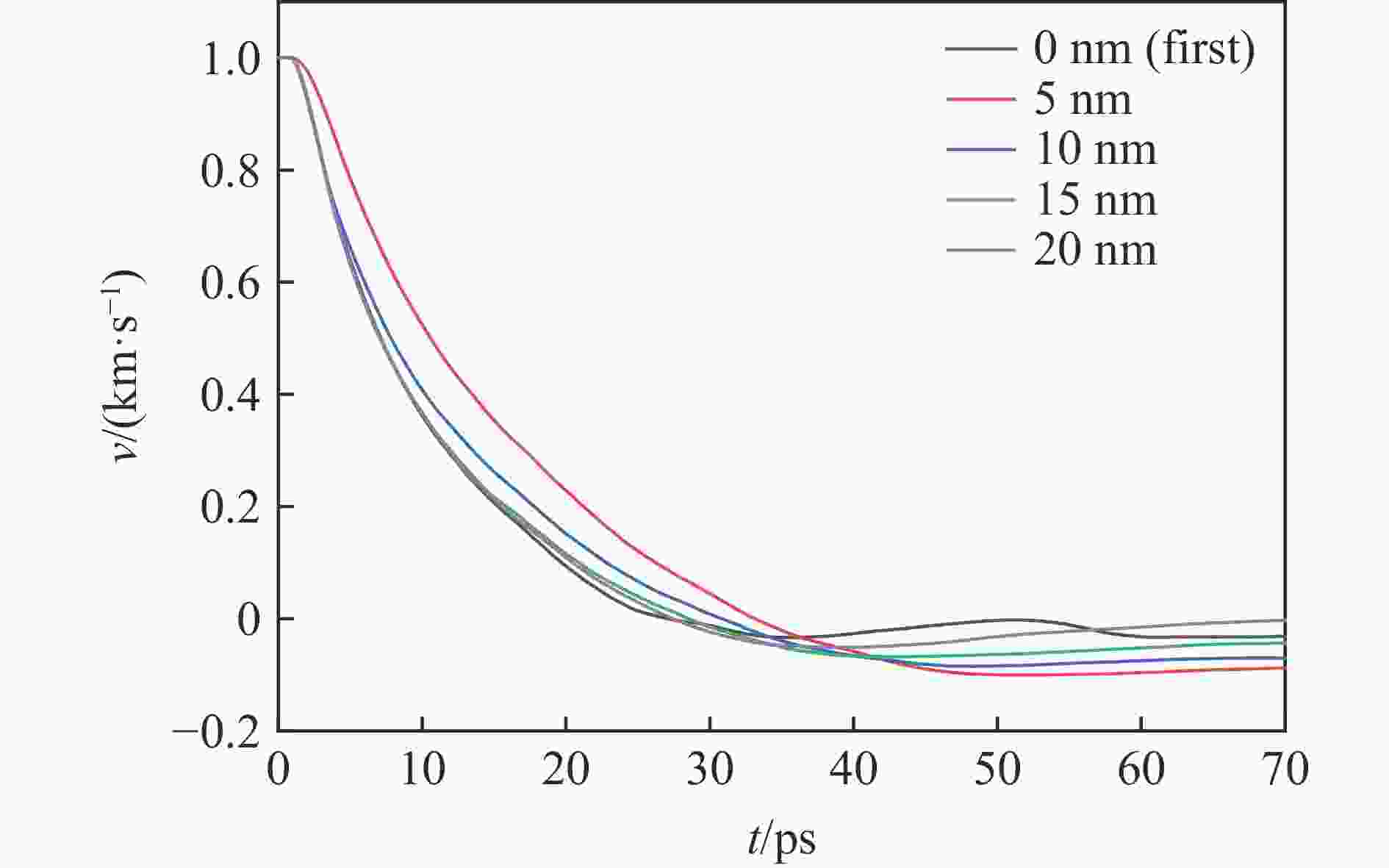
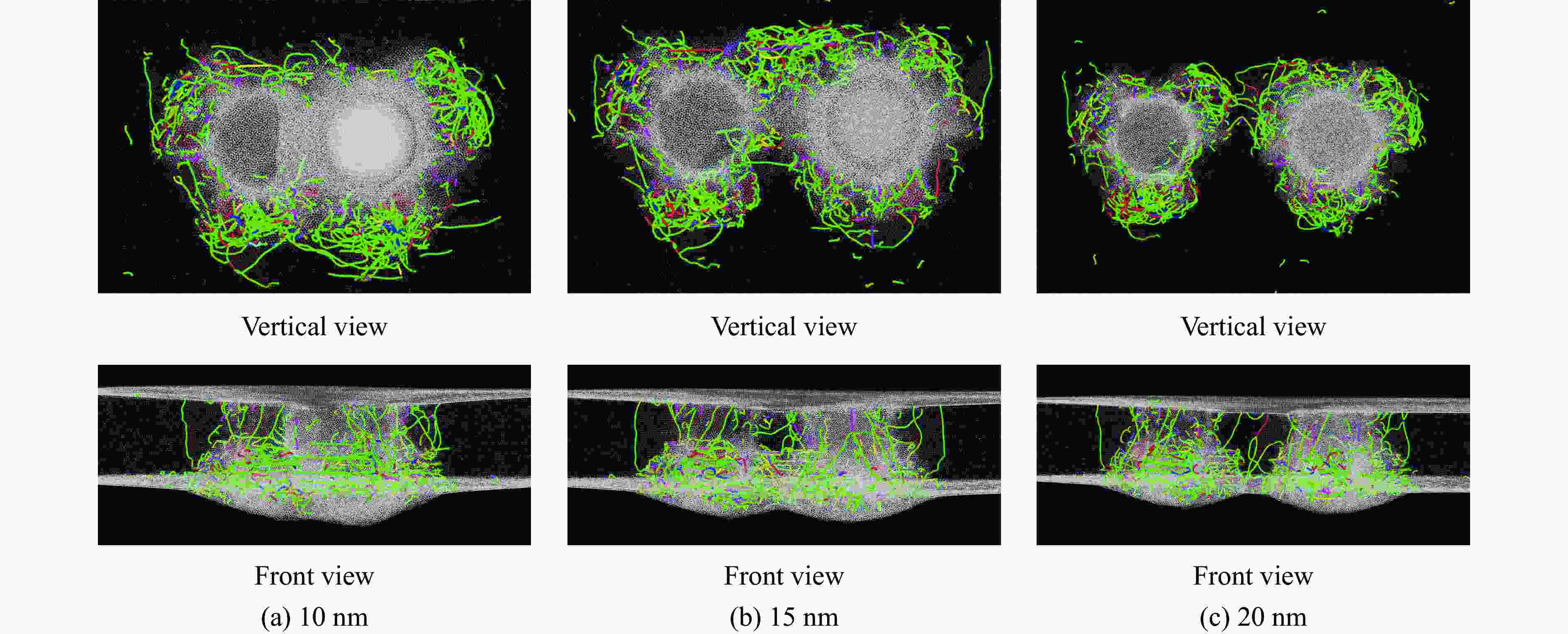
摘要: 为了揭示高熵合金（high-entropy alloy, HEA）在冲击载荷下的相结构演变、位错分布、能量吸收及冲击累积效应的变化规律，通过分子动力学模拟，系统探讨了Al0.3CoCrFeNi 高熵合金板在受单次及二次冲击载荷下的动态响应行为。结果显示，首次冲击下，Al0.3CoCrFeNi高熵合金板的塑性区域相结构演变和能量吸收方式具有显著的冲击速度依赖性。随着冲击速度的提高，面心立方相结构的比例呈现三阶段下降趋势，而无序化结构则相应增加。在低速（0.5~1.0 km/s）冲击下，能量主要通过位错网络进行吸收；在中速（1.0~2.0 km/s）冲击下，位错与无序化原子共同吸收能量；在高速（2.0~3.0 km/s）冲击下，无序化原子主导吸收能量。位错线长度在刚性球0.5~0.8 km/s的冲击速度范围内，随冲击速度呈线性增加，而在更高的速度冲击下，因HEA板厚度限制，位错线长度呈下降趋势。应力分析表明，冲击速度提高时，最大应力与塑性区域边界应力随着冲击速度的提高表现出非线性变化的二次关系。二次冲击下，几何特征方面，Al0.3CoCrFeNi 高熵合金板在冲击后形成类梯形的破坏区域，其上坑半径随冲击速度的变化呈现二次变化关系，二次冲击的最小影响区域也与冲击速度呈现二次关系；抗冲击性能方面，随着刚性球首次冲击速度的提高，其二次冲击后的剩余速度也随之上升，HEA板材料抵抗冲击性能降低。在距冲击中心10 nm处，HEA板的弹道极限随着首次冲击速度增加而非线性减小，然而，二次冲击速度的提高会使首次冲击的影响减弱。Abstract: To investigate the evolution of phase structure, dislocation distribution, energy absorption capacity, and impact accumulation effect of high-entropy alloys (HEA) under shock loading, molecular dynamics simulations were employed to systematically analyze the dynamic response behavior of Al0.3CoCrFeNi HEA plate subjected to single and secondary impact load. The results show that under the first impact, the phase structure evolution and energy absorption mode of the plastic region of Al0.3CoCrFeNi HEA plate exhibits significant velocity dependence. As the speed increases, the proportion of face-centered cubic structure shows a three-stage downward trend, while the disorder structure increases accordingly. Under low velocity impact (0.5-1.0 km/s), energy is mainly absorbed by dislocation network; at medium velocity impact (1.0-2.0 km/s), both dislocations and disordered atoms contribute; under high velocity impact (2.0-3.0 km/s), disordered atoms dominate energy absorption. Within the velocity range of 0.5-0.8 km/s of the rigid sphere, the dislocation line length increases linearly with the impact velocity. However, at higher impact velocities, the dislocation line length decreases due to the limitation of the plate thickness. The stress analysis shows that when the impact velocity increases, both the maximum stress and the boundary stress of the plastic zone exhibit nonlinear variations characterized by a quadratic relationship. Under the secondary impact, the Al0.3CoCrFeNi HEA plate forms a damage zone resembling a trapezoidal shape after impact. The radius of the pit within this damage zone exhibits a quadratic relationship with the impact velocity. Additionally, the minimum affected area resulting from the secondary impact also demonstrates a quadratic relationship with the impact velocity. Regarding impact resistance, as the initial impact velocity increases, the residual velocity following the secondary impact also rises, indicating a reduction in the resistance capability of HEA. At a distance of 10 nm from the impact center, the ballistic limit velocity decreases nonlinearly with increasing initial impact velocity. However, an increase in the secondary impact velocity mitigates the effects induced by the initial impact.
-
Key words:
- high entropy alloy /
- repeated impact /
- molecular dynamics /
- dynamic defect evolution /
- cumulative damage
-
图 2 不同初始速度的刚性球在冲击HEA板的过程中速度随时间的变化
Figure 2. Velocity-time histories of rigid balls with different initial velocities in their impact processes on HEA plates
图 3 HEA板受不同初始速度刚性球冲击后的相结构分布
Figure 3. Phase structure distributions of HEA plates impacted by rigid balls with different initial velocities
图 4 被刚性球以1 km/s的速度冲击后HEA板相结构占比的变化
Figure 4. Changes in the proportion of HEA plate phase structure after being impacted by a rigid ball at a velocity of 1 km/s
图 5 被不同初始速度的刚性球冲击后HEA板主要相结构占比的变化
Figure 5. Changes in the proportion of the main phase structures of HEA plates after being impacted by rigid balls with different initial velocities
图 6 HEA板受不同初始速度刚性球冲击后的位错分布
Figure 6. Dislocation distribution of HEA plates impacted by rigid balls with different initial velocities
图 7 HEA板受初始速度为0.5～3.0 km/s的刚性球冲击过程中的位错线长度变化
Figure 7. Changes in dislocation line length of a HEA plate during the impact process of a rigid ball with an initial velocity of 0.5–3.0 km/s on it
图 8 HEA板受刚性球冲击后的损伤及塑性变化示意图
Figure 8. Schematic diagram of damage and plastic deformation in a HEA plate impacted by a rigid ball
图 9 HEA板塑性变形半径随刚性球冲击速度的变化
Figure 9. The radius of plastic deformation in a HEA plate varied with the impact velocity of a rigid ball
图 10 HEA板受不同初始的速度刚性球冲击后的应力分布
Figure 10. Stress distribution in HEA plates impacted by rigid balls with different initial velocities
图 11 受初始速度为0.7 km/s的刚性球冲击过程中HEA板撞击区域内的应力随时间的变化图谱以及刚性球的速度随时间的变化
Figure 11. Graph of stress variation over time in the HEA plate impact area during the impact process of a rigid sphere with an initial velocity of 0.7 km/s, as well as the variation of the velocity of the rigid sphere over time
图 12 受初始速度为1.0 km/s的刚性球冲击过程中HEA板撞击区域内的应力随时间的变化图谱以及刚性球的速度随时间的变化
Figure 12. Graph of stress variation over time in the HEA plate impact area during the impact process of a rigid sphere with an initial velocity of 1.0 km/s, as well as the variation of the velocity of the rigid sphere over time
图 13 受初始速度为2.0 km/s的刚性球冲击过程中HEA板撞击区域内的应力随时间的变化图谱以及刚性球的速度随时间的变化
Figure 13. Graph of stress variation over time in the HEA plate impact area during the impact process of a rigid sphere with an initial velocity of 2.0 km/s, as well as the variation of the velocity of the rigid sphere over time
图 14 HEA板应力与刚性球冲击速度的关系
Figure 14. Relation between stress in a HEA plate and impact velocity of a rigid ball
图 15 HEA板受刚性球1.0 km/s的速度二次冲击不同位置后的相结构分布
Figure 15. Phase structure distribution of the HEA plate after secondary impact by a rigid ball at the velocity of 1.0 km/s on different positions of it
图 16 刚性球以1.0 km/s的速度二次冲击HEA板不同位置后速度随时间的变化
Figure 16. Velocity-time histories of a rigid ball impacting different positions of the HEA plate at the impact velocity of 1.0 km/s
图 17 HEA板受刚性球1.0 km/s的速度二次冲击不同位置的位错分布
Figure 17. Dislocation distribution of the HEA plate after secondary impact by a rigid ball at the velocity of 1.0 km/s at different positions
图 18 HEA板受刚性球以1.0 km/s的速度二次冲击不同位置后位错线长度随时间的变化
Figure 18. Dislocation line length-time histories of the HEA plate after secondary impact by a rigid ball at the velocity of 1.0 km/s on it at different positions
图 19 二次冲击不受首次冲击影响的最小距离示意图
Figure 19. Schematic diagram of the minimum distance where the second impact is unaffected by the first impact
图 20 不同速度二次冲击后距首次冲击中心10 nm处的剩余速度
Figure 20. Remaining velocity at a distance of 10 nm from the center of the first impact after secondary impact at different velocities
图 21 HEA板受刚性球不同初始速度冲击后距HEA板中心10 nm处的弹道极限
Figure 21. The ballistic limit at 10 nm from the center of the HEA plate impacted by the rigid ball at different initial speeds
图 22 HEA板受刚性球不同初始速度冲击后距HEA板中心10 nm处的弹道极限
Figure 22. Ballistic limit at 10 nm from the center of the HEA plate impacted by the rigid ball at different initial velocities
图 23 首次冲击对二次冲击影响总结
Figure 23. Summary of the influence of the first impact on the secondary impact
表 1 不同原子对之间相互作用的Lennard-Jones参数
Table 1. Lennard-Jones parameters for interactions between different atom pairs
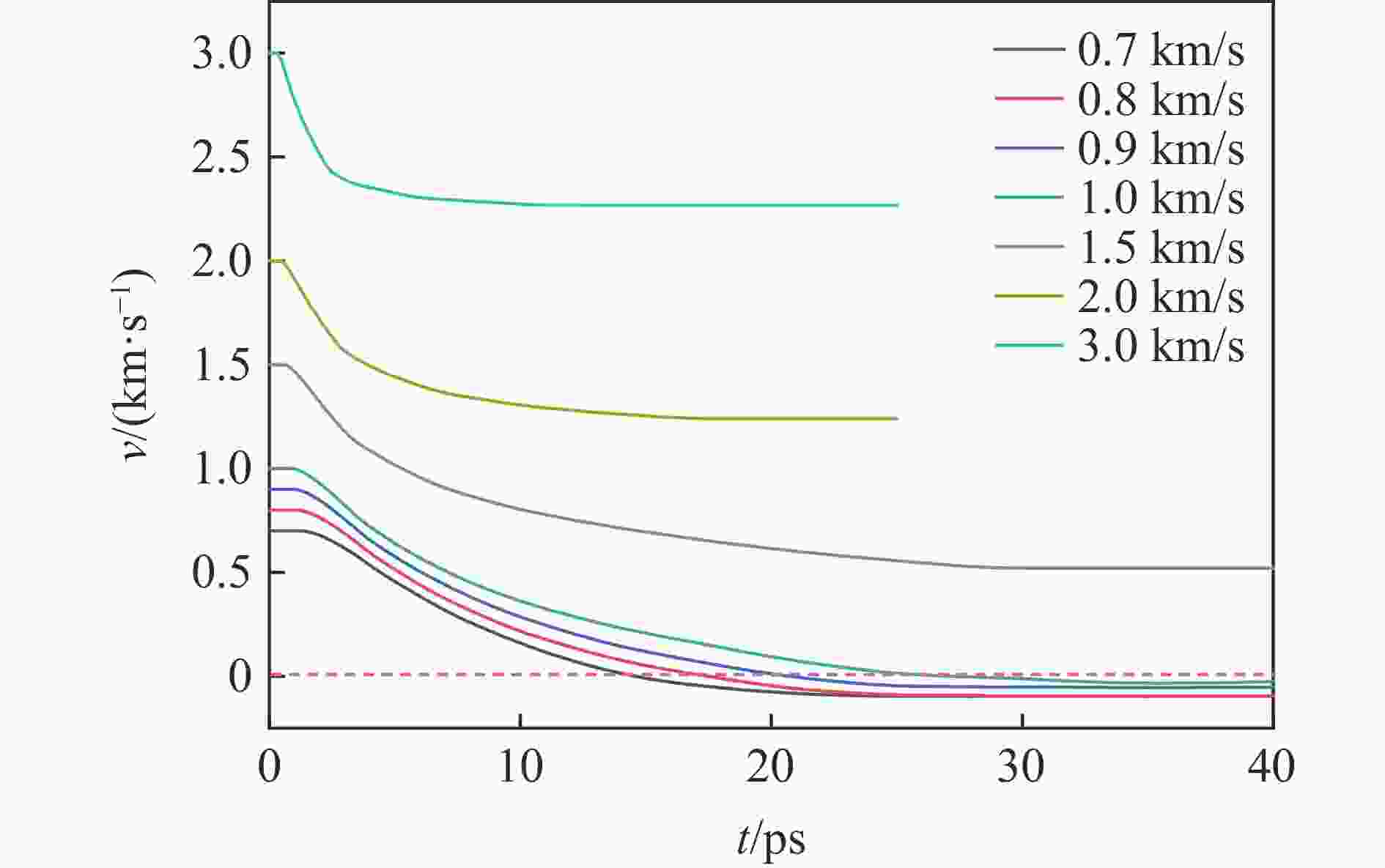
原子对 ε/eV σ/Å Al-Co 0.0469 2.578 Cr-Co 0.0466 2.456 Fe-Co 0.0477 2.448 Co-Co 0.0043 2.584 Ni-Co 0.0474 2.428 
下载: 导出CSV
表 2 不同初始速度刚性球冲击HEA板过程中刚性球的速度变化以及相应的时间信息
Table 2. Velocity variation of rigid balls with different initial velocities during their impact on HEA plates as well as the corresponding time formation
vi1/(km·s−1) tp/ps t0/ps vr/(km·s−1) (vi1-vr)2/(km·s−1)2 vi1/(km·s−1) tp/ps t0/ps vr/(km·s−1) (vi1-vr)2/(km·s−1)2 0.7 -- 14.4 0 0.49 1.5 31.7 -- 0.519 1.980 639 0.8 -- 17.4 0 0.64 2.0 18.4 -- 1.240 2.462 400 0.9 -- 19.8 0 0.81 3.0 11.9 -- 2.268 3.856 176 1.0 -- 26.3 0 1.00
下载: 导出CSV
表 3 HEA板受不同初始速度刚性球冲击后不同相结构的占比
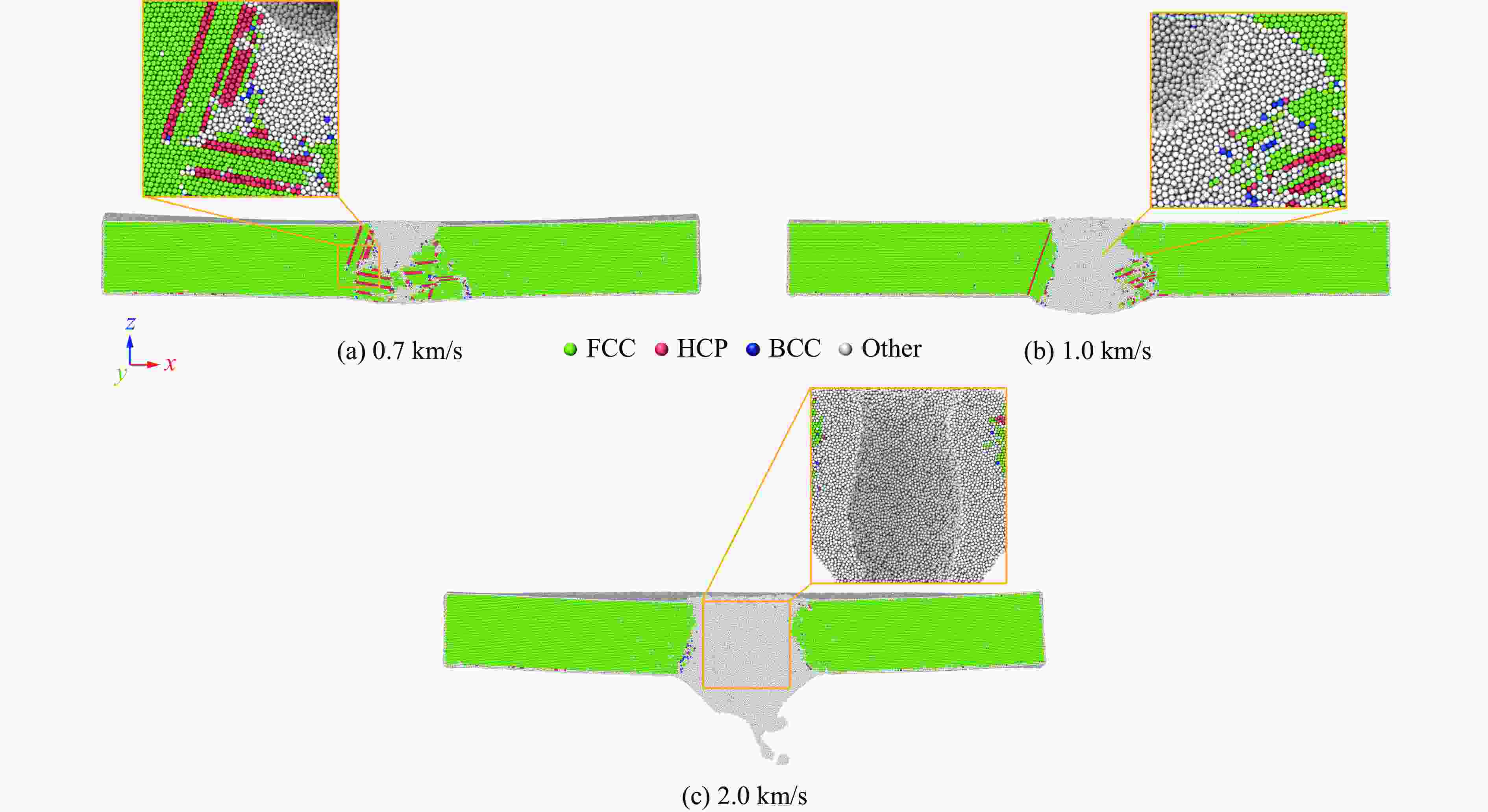
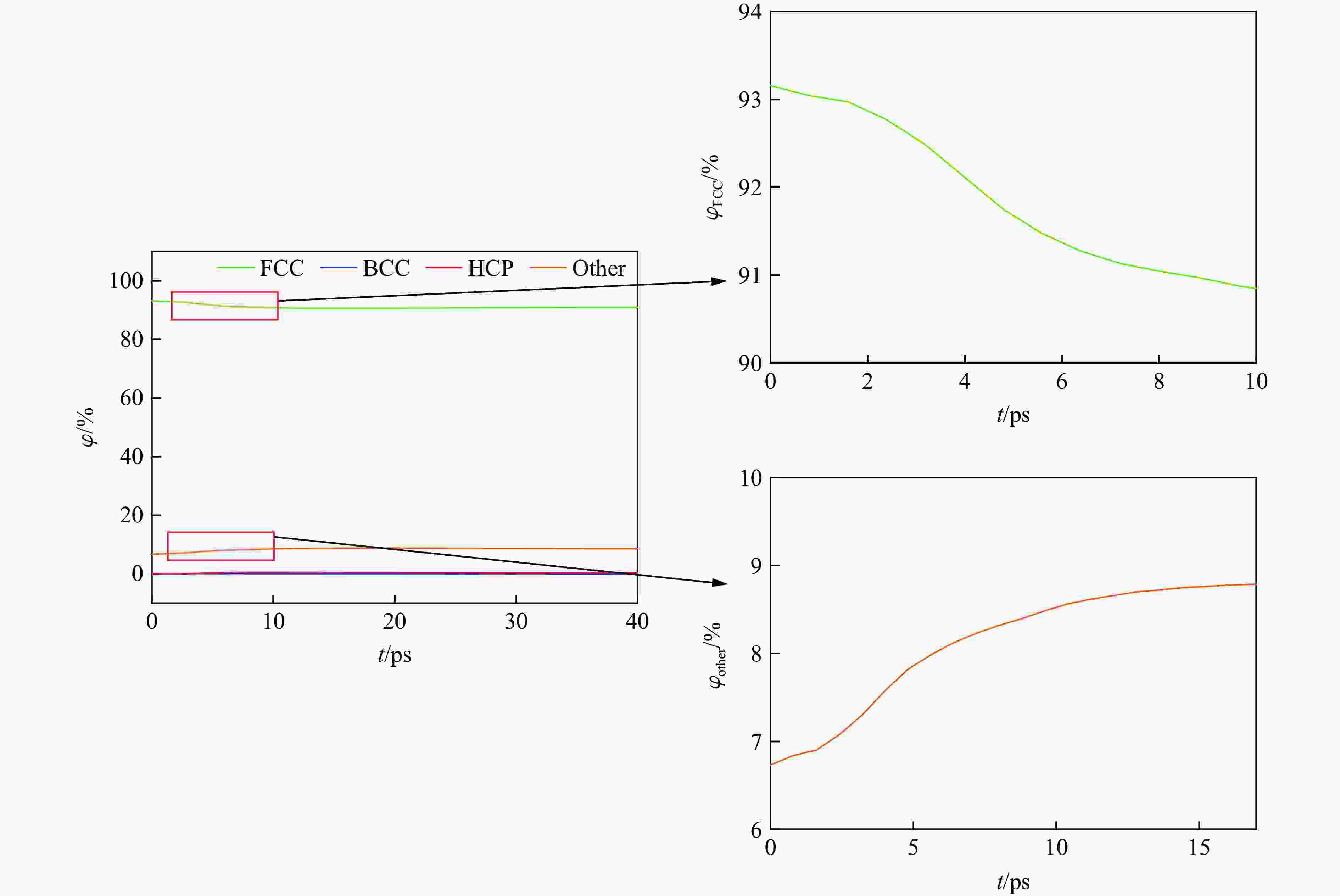
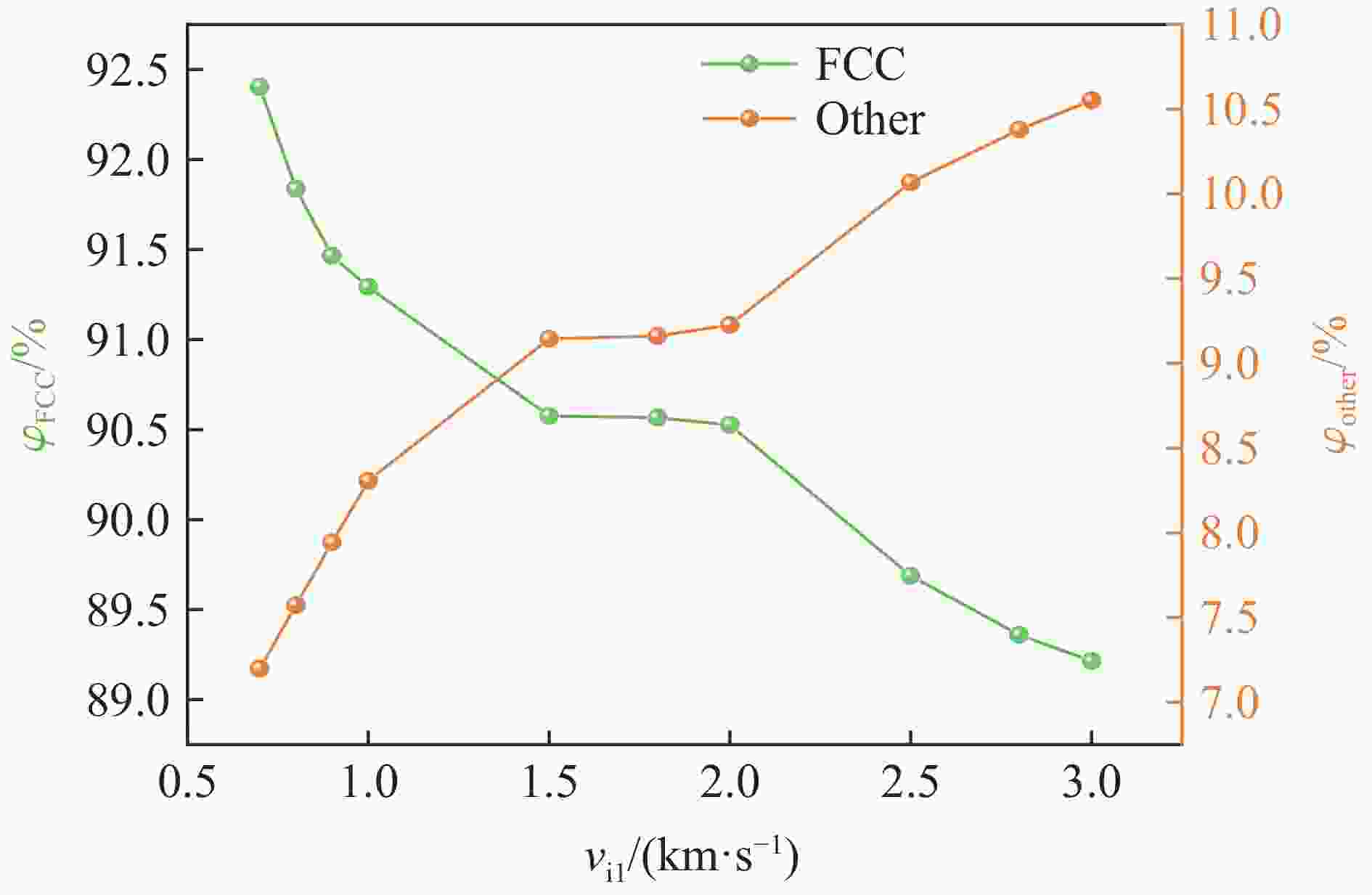
Table 3. Proportions of different phase structures of HEA plates impacted by rigid balls with different initial velocities
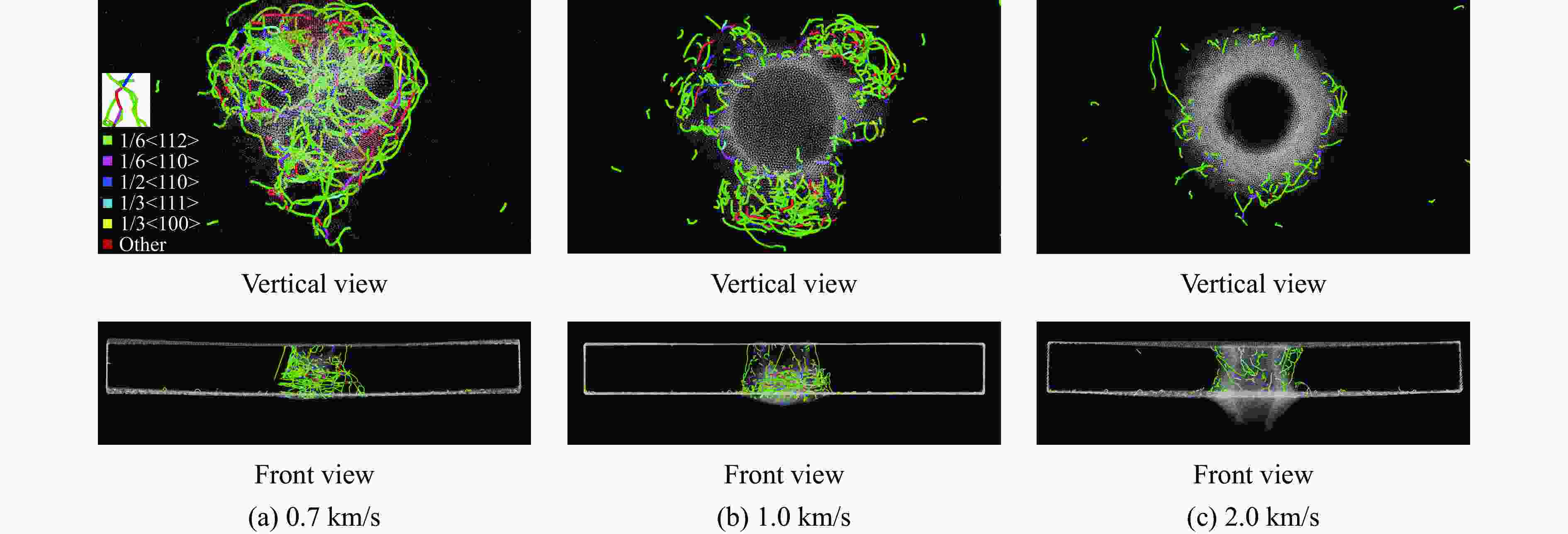
vi1/(km·s−1) ϕ/% vi1/(km·s−1) ϕ/% FCC BCC HCP Other FCC BCC HCP Other 0.7 92.40404 0.03169 0.36583 7.19843 1.8 90.56659 0.03882 0.23237 9.16181 0.8 91.83749 0.04834 0.54063 7.57346 2.0 90.52505 0.03584 0.21256 9.22619 0.9 91.46428 0.06413 0.52804 7.94337 2.5 89.68800 0.04055 0.20395 10.0671 1.0 91.29216 0.05186 0.34857 8.30707 2.8 89.35985 0.03970 0.22055 10.37958 1.5 90.57492 0.03554 0.24414 9.14491 3.0 89.21314 0.04293 0.19173 10.55185
下载: 导出CSV
表 4 HEA板受不同初始速度刚性球冲击后的最长位错线长度和最终位错线长度及达到最长位错长度所需的时间
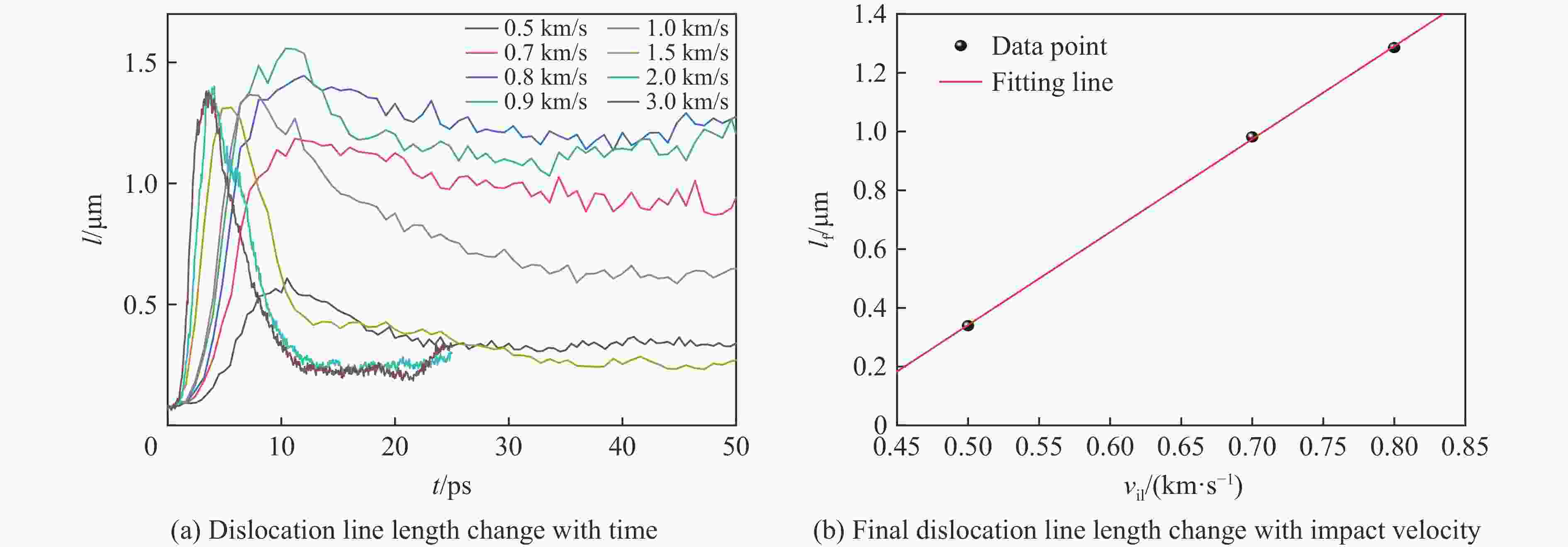
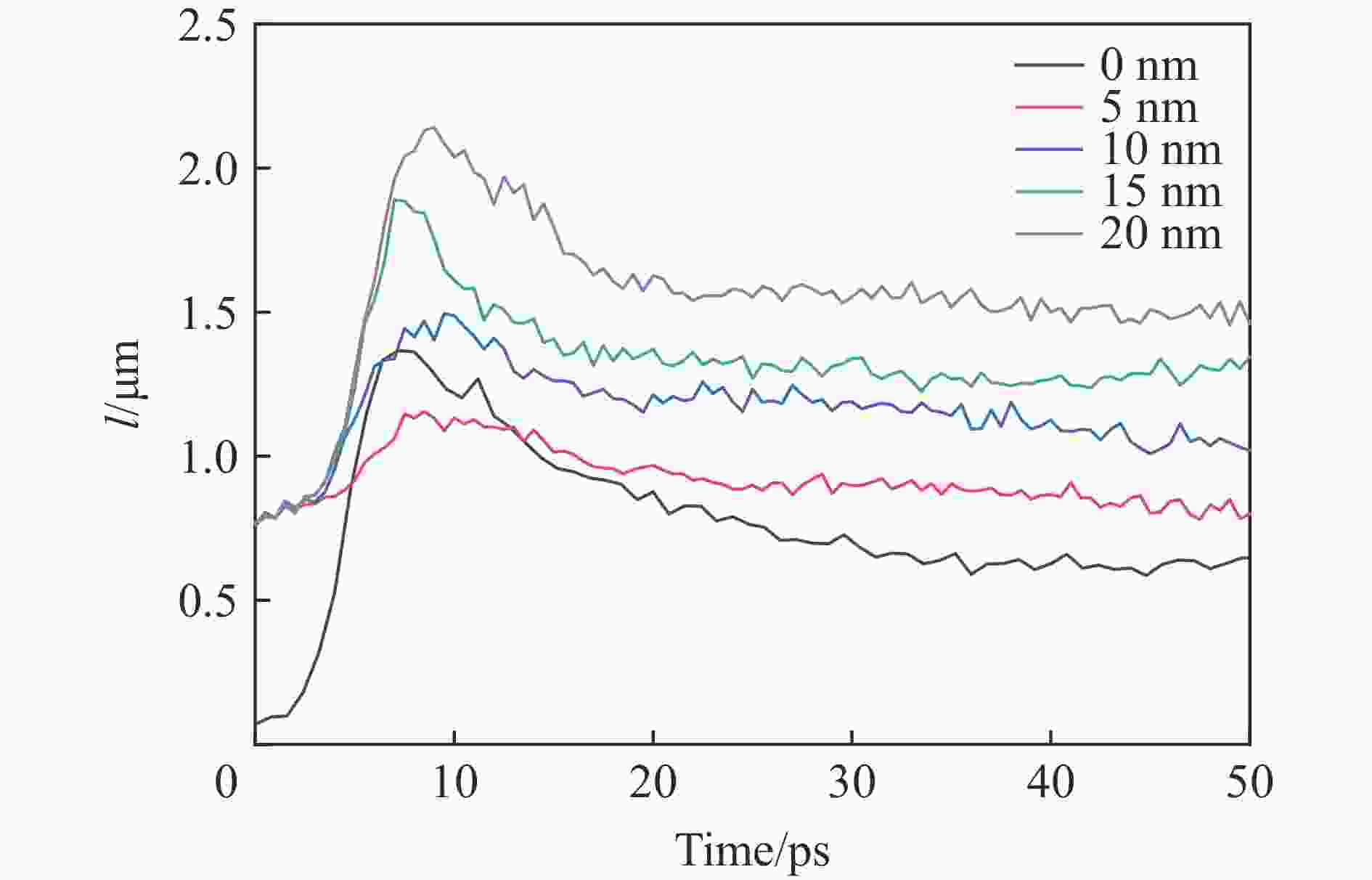
Table 4. The maximum and final dislocation line lengths of HEA plates impacted by rigid balls with different initial velocities as well as the time required to reach the maximum dislocation line length
vi1/(km·s−1) lmax/nm $ {t}_{{l}_{\mathrm{m}\mathrm{a}\mathrm{x}}} $/ps lf/nm vi1/(km·s−1) lmax/nm $ {t}_{{l}_{\mathrm{m}\mathrm{a}\mathrm{x}}} $/ps lf/nm 0.5 607.9 10.5 339.1 1.0 1366.5 7.2 646.5 0.7 1185.2 11.2 981.4 1.5 1313.1 5.6 234.1 0.8 1445.2 12.0 1285.5 2.0 1395.4 4.0 247.7 0.9 1557.4 10.4 1143.2 3.0 1376.1 3.5 239.3
下载: 导出CSV
表 5 刚性球以1.0 km/s的速度二次冲击 HEA板不同位置后的速度降为零所需的时间和其反弹速度及HEA板的最长位错线长度
Table 5. Time required for the velocity of a rigid ball to drop to zero and its rebound velocity as well as the longest dislocation line length of the HEA plate by secondary impact on different positions at a velocity of 1.0 km/s
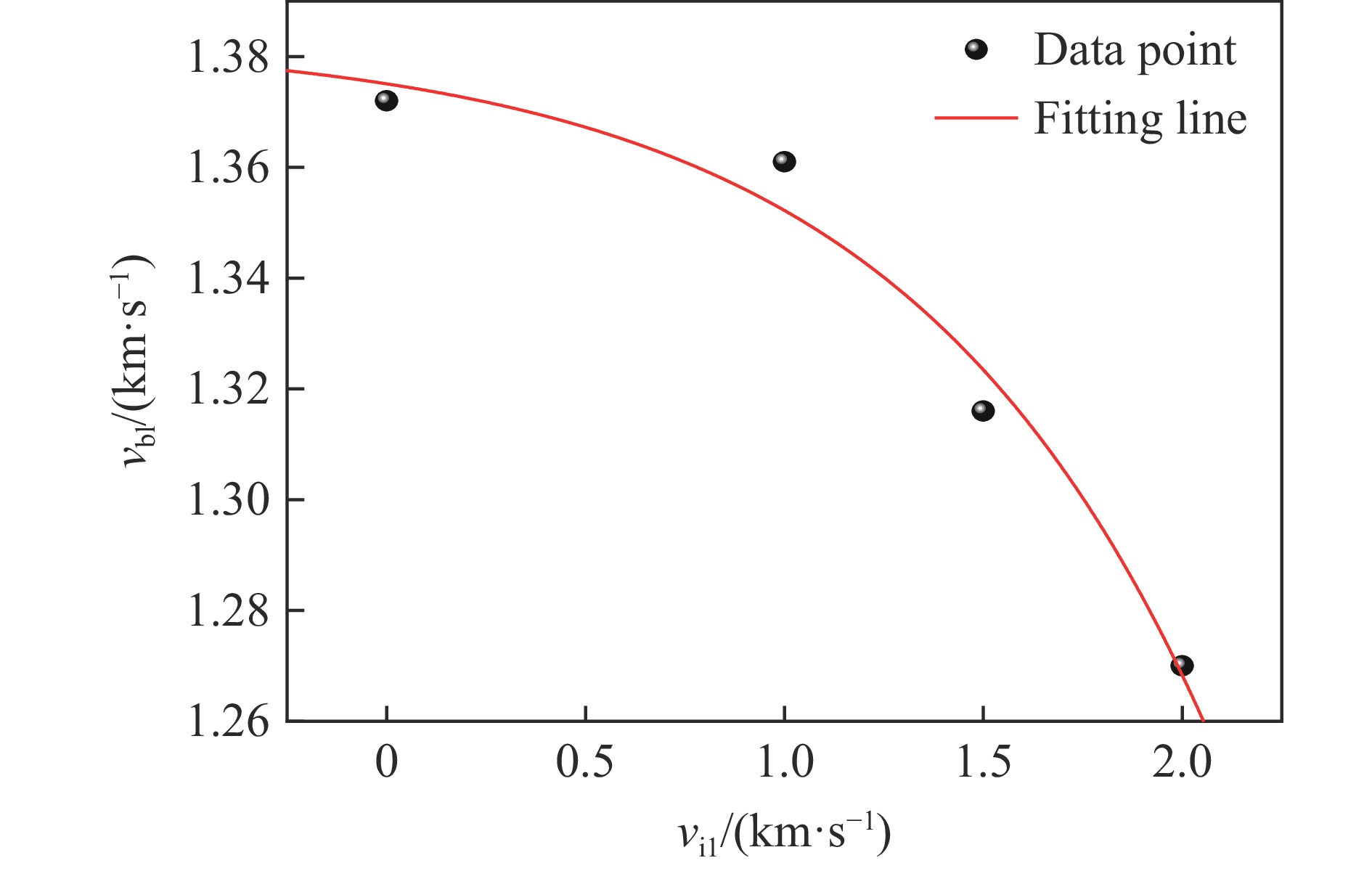
S/nm t0/ps vreb/(m·s−1) lmax/mm 0 26.3 17.9 6.465 5 33.1 79.2 7.994 10 30.8 66.3 10.192 15 28.5 40.9 13.433 20 27.4 5.3 14.612
下载: 导出CSV
表 6 HEA板受刚性球不同初始速度冲击后距HEA板中心10 nm处的弹道极限数据
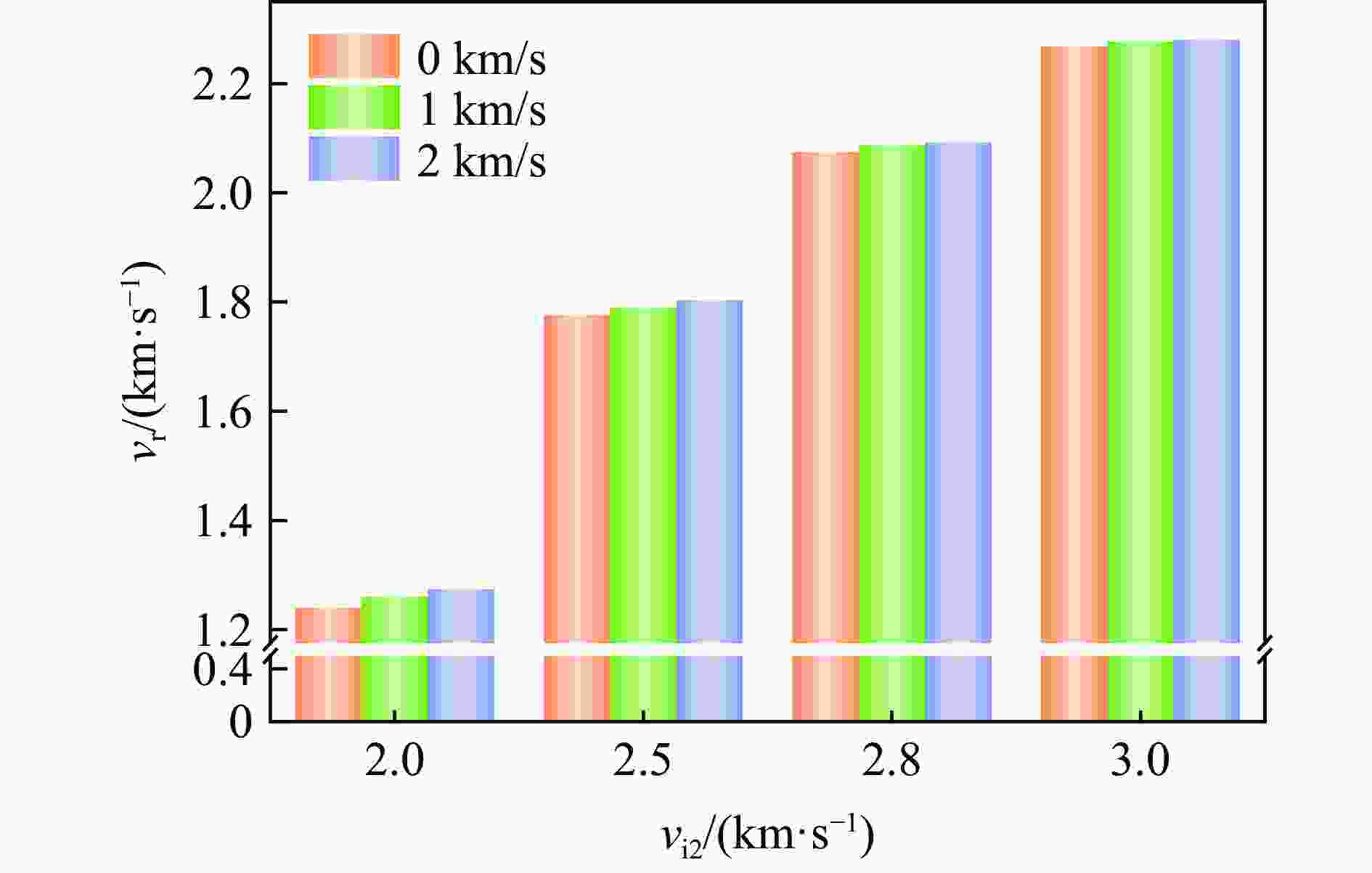
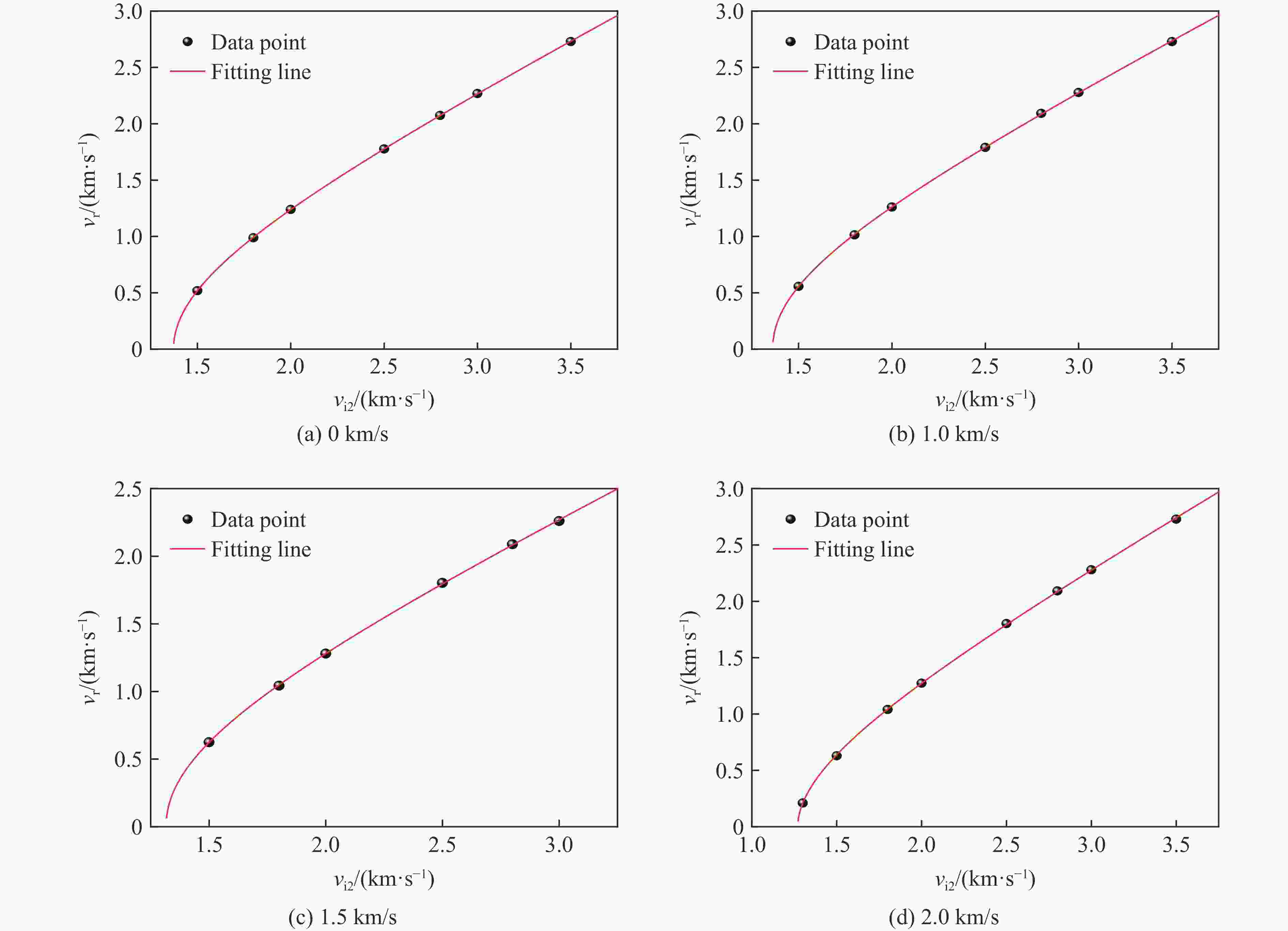
Table 6. The ballistic limit at 10 nm from the center of the HEA plate impacted by the rigid ball at different initial velocities
vi1/
(km·s−1)vi2/
(km·s−1)vr
(km·s−1)vbl/
(km·s−1)a p vi1/
(km·s−1)vi2/
(km·s−1)vr/
(km·s−1)vbl/
(km·s−1)a p 0 1.5 0.519 1.372 0.72 2.01 1.0 1.5 0.557 1.361 0.7 2.08 1.8 0.988 1.8 1.014 2.0 1.240 2.0 1.261 2.5 1.776 2.5 1.790 2.8 2.074 2.8 2.092 3.0 2.268 3.0 2.277 3.5 2.729 3.5 2.729 vi1/
(km·s−1)vi2/
(km·s−1)vr
(km·s−1)vbl/
(km·s−1)a p vi1/
(km·s−1)vi2/
(km·s−1)vr
(m·s−1)vbl/
(km·s−1)a p 1.5 1.5 0.625 1.316 0.68 2.07 2.0 1.3 0.211 1.270 0.74 1.89 1.8 1.043 1.5 0.629 2.0 1.280 1.8 1.040 2.5 1.803 2.0 1.274 2.8 2.089 2.5 1.803 3.0 2.260 2.8 2.092 -- -- 3.0 2.280 -- -- 3.5 2.729
下载: 导出CSV
-
[1] DU M, LIU B, LIU Y, et al. Dynamic behavior of additively manufactured FeCoCrNi high entropy alloy [J]. Metals, 2023, 13(1): 75. DOI: 10.3390/met13010075. [2] HE J Y, WANG Q, ZHANG H S, et al. Dynamic deformation behavior of a face-centered cubic FeCoNiCrMn high-entropy alloy [J]. Science Bulletin, 2018, 63(6): 362–368. DOI: 10.1016/j.scib.2018.01.022. [3] SONG S W, LI H T, LIU P W, et al. Dynamic shock response of high-entropy alloy with elemental anomaly distribution [J]. International Journal of Mechanical Sciences, 2023, 253: 108408. DOI: 10.1016/j.ijmecsci.2023.108408. [4] WU Y Q, LIAW P K, LI R X, et al. Relationship between the unique microstructures and behaviors of high-entropy alloys [J]. International Journal of Minerals, Metallurgy and Materials, 2024, 31(6): 1350–1363. DOI: 10.1007/s12613-023-2777-4. [5] LI Z Z, ZHAO S T, RITCHIE R O, et al. Mechanical properties of high-entropy alloys with emphasis on face-centered cubic alloys [J]. Progress in Materials Science, 2019, 102: 296–345. DOI: 10.1016/j.pmatsci.2018.12.003. [6] CAO T Q, ZHANG Q, WANG L, et al. Dynamic deformation behaviors and mechanisms of CoCrFeNi high-entropy alloys [J]. Acta Materialia, 2023, 260: 119343. DOI: 10.1016/j.actamat.2023.119343. [7] FAN H D, WANG Q Y, EL-AWADY J A, et al. Strain rate dependency of dislocation plasticity [J]. Nature Communications, 2021, 12(1): 1845. DOI: 10.1038/s41467-021-21939-1. [8] JIANG K, LI J G, KAN X K, et al. Adiabatic shear localization induced by dynamic recrystallization in an FCC high entropy alloy [J]. International Journal of Plasticity, 2023, 162: 103550. DOI: 10.1016/j.ijplas.2023.103550. [9] SHEN Y X, SPEAROT D E. Mobility of dislocations in FeNiCrCoCu high entropy alloys [J]. Modelling and Simulation in Materials Science and Engineering, 2021, 29(8): 085017. DOI: 10.1088/1361-651X/ac336a. [10] HAN Y, LI H B, FENG H, et al. Mechanism of dislocation evolution during plastic deformation of nitrogen-doped CoCrFeMnNi high-entropy alloy [J]. Materials Science and Engineering: A, 2021, 814: 141235. DOI: 10.1016/j.msea.2021.141235. [11] LI Z M, TASAN C C, SPRINGER H, et al. Interstitial atoms enable joint twinning and transformation induced plasticity in strong and ductile high-entropy alloys [J]. Scientific Reports, 2017, 7: 40704. DOI: 10.1038/srep40704. [12] SHI K W, CHENG J C, CUI L, et al. Ballistic impact response of Fe40Mn20Cr20Ni20 high-entropy alloys [J]. Journal of Applied Physics, 2022, 132(20): 205105. DOI: 10.1063/5.0130634. [13] SONAR T, IVANOV M, TROFIMOV E, et al. An overview of microstructure, mechanical properties and processing of high entropy alloys and its future perspectives in aeroengine applications [J]. Materials Science for Energy Technologies, 2024, 7: 35–60. DOI: 10.1016/j.mset.2023.07.004. [14] FARAHANI M G, RIZI M B, AGHAAHMADI M, et al. Activation of different twinning mechanisms and their contributions to mechanical behavior of a face-centered cubic Co-based high-entropy alloy [J]. Acta Materialia, 2025, 285: 120665. DOI: 10.1016/j.actamat.2024.120665. [15] ZHAO S T, LI Z Z, ZHU C Y, et al. Amorphization in extreme deformation of the CrMnFeCoNi high-entropy alloy [J]. Science Advances, 2021, 7(5): eabb3108. DOI: 10.1126/sciadv.abb3108. [16] LV Y K, SONG P T, WANG Y Z, et al. Improving mechanical properties of Fe-Mn-Co-Cr high-entropy alloy via annealing after cold rolling [J]. Materials, 2024, 17(3): 676. DOI: 10.3390/ma17030676. [17] HE F, WANG Z J, CHENG P, et al. Designing eutectic high entropy alloys of CoCrFeNiNbX [J]. Journal of Alloys and Compounds, 2016, 656: 284–289. DOI: 10.1016/j.jallcom.2015.09.153. [18] CHEN S J, OH H S, GLUDOVATZ B, et al. Real-time observations of TRIP-induced ultrahigh strain hardening in a dual-phase CrMnFeCoNi high-entropy alloy [J]. Nature Communications, 2020, 11(1): 826. DOI: 10.1038/s41467-020-14641-1. [19] ZHOU C S, KOU Z D, SONG K K, et al. Evading strength-ductility trade-off dilemma in TRIP-assisted Fe50Mn30Co10Cr10 duplex high-entropy alloys via flash annealing and deep cryogenic treatments [J]. Acta Materialia, 2024, 268: 119779. DOI: 10.1016/j.actamat.2024.119779. [20] MUSKERI S, GWALANI B, JHA S, et al. Excellent ballistic impact resistance of Al0.3CoCrFeNi multi-principal element alloy with unique bimodal microstructure [J]. Scientific Reports, 2021, 11(1): 22715. DOI: 10.1038/s41598-021-02209-y. [21] GAO X Z, LU Y P, ZHANG B, et al. Microstructural origins of high strength and high ductility in an AlCoCrFeNi2.1 eutectic high-entropy alloy [J]. Acta Materialia, 2017, 141: 59–66. DOI: 10.1016/j.actamat.2017.07.041. [22] ZHANG W R, LIAW P K, ZHANG Y. Science and technology in high-entropy alloys [J]. Science China Materials, 2018, 61(1): 2–22. DOI: 10.1007/s40843-017-9195-8. [23] LI R N, SONG H Y, AN M R, et al. Atomic-scale insight into mechanical properties and deformation behavior of crystalline/amorphous dual-phase high entropy alloys [J]. Physics Letters A, 2022, 446: 128272. DOI: 10.1016/j.physleta.2022.128272. [24] CHEN Y, RENG S W, PENG J, et al. Chemical short range order and deformation mechanism of a refractory high entropy alloy HfNbTaZr under nanoindentation: an atomistic study [J]. Journal of Materials Research and Technology, 2023, 24: 3588–3598. DOI: 10.1016/j.jmrt.2023.04.074. [25] SUN Z R, SHI C G, LIU C X, et al. The effect of short-range order on mechanical properties of high entropy alloy Al0.3CoCrFeNi [J]. Materials & Design, 2022, 223: 111214. DOI: 10.1016/j.matdes.2022.111214. [26] WU Y C, SHAO J L. FCC-BCC phase transformation induced simultaneous enhancement of tensile strength and ductility at high strain rate in high-entropy alloy [J]. International Journal of Plasticity, 2023, 169: 103730. DOI: 10.1016/j.ijplas.2023.103730. [27] KOSTIUCHENKO T, KÖRMANN F, NEUGEBAUER J, et al. Impact of lattice relaxations on phase transitions in a high-entropy alloy studied by machine-learning potentials [J]. npj Computational Materials, 2019, 5(1): 55. DOI: 10.1038/s41524-019-0195-y. [28] LI L, CHEN H T, FANG Q H, et al. Effects of temperature and strain rate on plastic deformation mechanisms of nanocrystalline high-entropy alloys [J]. Intermetallics, 2020, 120: 106741. DOI: 10.1016/j.intermet.2020.106741. [29] LI W H, XIANG M Z, AITKEN Z H, et al. Unraveling the Hall-Petch to inverse Hall-Petch transition in nanocrystalline high entropy alloys under shock loading [J]. International Journal of Plasticity, 2024, 178: 104010. DOI: 10.1016/j.ijplas.2024.104010. [30] 闻鹏, 陶钢. 温度对CoCrFeMnNi高熵合金冲击响应和塑性变形机制影响的分子动力学研究 [J]. 物理学报, 2022, 71(24): 246101. DOI: 10.7498/aps.71.20221621.WEN P, TAO G. Molecular dynamics study of temperature effects on shock response and plastic deformation mechanism of CoCrFeMnNi high-entropy alloys [J]. Acta Physica Sinica, 2022, 71(24): 246101. DOI: 10.7498/aps.71.20221621. [31] WEN P, DU C X, TAO G, et al. Effect of Mn element on shock response in CoCrFeNiMnx high entropy alloys [J]. Chinese Physics B, 2024, 33(11): 116103. DOI: 10.1088/1674-1056/ad7fd0. [32] LI W H, CHEN S, AITKEN Z, et al. Shock-induced deformation and spallation in CoCrFeMnNi high-entropy alloys at high strain-rates [J]. International Journal of Plasticity, 2023, 168: 103691. DOI: 10.1016/j.ijplas.2023.103691. [33] CHEN X, LIU L, GAO R J, et al. Molecular dynamics simulation of the heterostructure of the CoCrFeMnNi high entropy alloy under an impact load [J]. Modelling and Simulation in Materials Science and Engineering, 2023, 31(8): 085020. DOI: 10.1088/1361-651X/ad084d. [34] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics [J]. Journal of Computational Physics, 1995, 117(1): 1–19. DOI: 10.1006/jcph.1995.1039. [35] FARKAS D, CARO A. Model interatomic potentials for Fe-Ni-Cr-Co-Al high-entropy alloys [J]. Journal of Materials Research, 2020, 35(22): 3031–3040. DOI: 10.1557/jmr.2020.294. [36] YANG Y C, LIU C X, LIN C Y, et al. The effect of local atomic configuration in high-entropy alloys on the dislocation behaviors and mechanical properties [J]. Materials Science and Engineering: A, 2021, 815: 141253. DOI: 10.1016/j.msea.2021.141253. [37] JONES J E. On the determination of molecular fields: Ⅱ. from the equation of state of a gas [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1924, 106(738): 463–477. DOI: 10.1098/rspa.1924.0082. [38] FAKEN D, JÓNSSON H. Systematic analysis of local atomic structure combined with 3D computer graphics [J]. Computational Materials Science, 1994, 2(2): 279–286. DOI: 10.1016/0927-0256(94)90109-0. [39] STUKOWSKI A. Structure identification methods for atomistic simulations of crystalline materials [J]. Modelling and Simulation in Materials Science and Engineering, 2012, 20(4): 045021. DOI: 10.1088/0965-0393/20/4/045021. [40] TANG Y Q, LI D Y. Dynamic response of high-entropy alloys to ballistic impact [J]. Science Advances, 2022, 8(32): eabp9096. DOI: 10.1126/sciadv.abp9096. [41] LIANG Z Y, WANG X, HUANG W, et al. Strain rate sensitivity and evolution of dislocations and twins in a twinning-induced plasticity steel [J]. Acta Materialia, 2015, 88: 170–179. DOI: 10.1016/j.actamat.2015.01.013. [42] LI X Y, WEI Y J, LU L, et al. Dislocation nucleation governed softening and maximum strength in nano-twinned metals [J]. Nature, 2010, 464(7290): 877–880. DOI: 10.1038/nature08929. [43] MONAVARI M, ZAISER M. Annihilation and sources in continuum dislocation dynamics [J]. Materials Theory, 2018, 2(1): 3. DOI: 10.1186/s41313-018-0010-z. [44] ANDERSON JR C E. Analytical models for penetration mechanics: a review [J]. International Journal of Impact Engineering, 2017, 108: 3–26. DOI: 10.1016/j.ijimpeng.2017.03.018. [45] RECHT R F, IPSON T W. Ballistic perforation dynamics [J]. Journal of Applied Mechanics, 1963, 30(3): 384–390. DOI: 10.1115/1.3636566. -
计量
- 文章访问数: 37
- HTML全文浏览量: 7
- PDF下载量: 25
- 被引次数: 0