Machine learning-driven low-velocity impact response prediction and multi-objective optimization of origami metamaterial sandwich
-
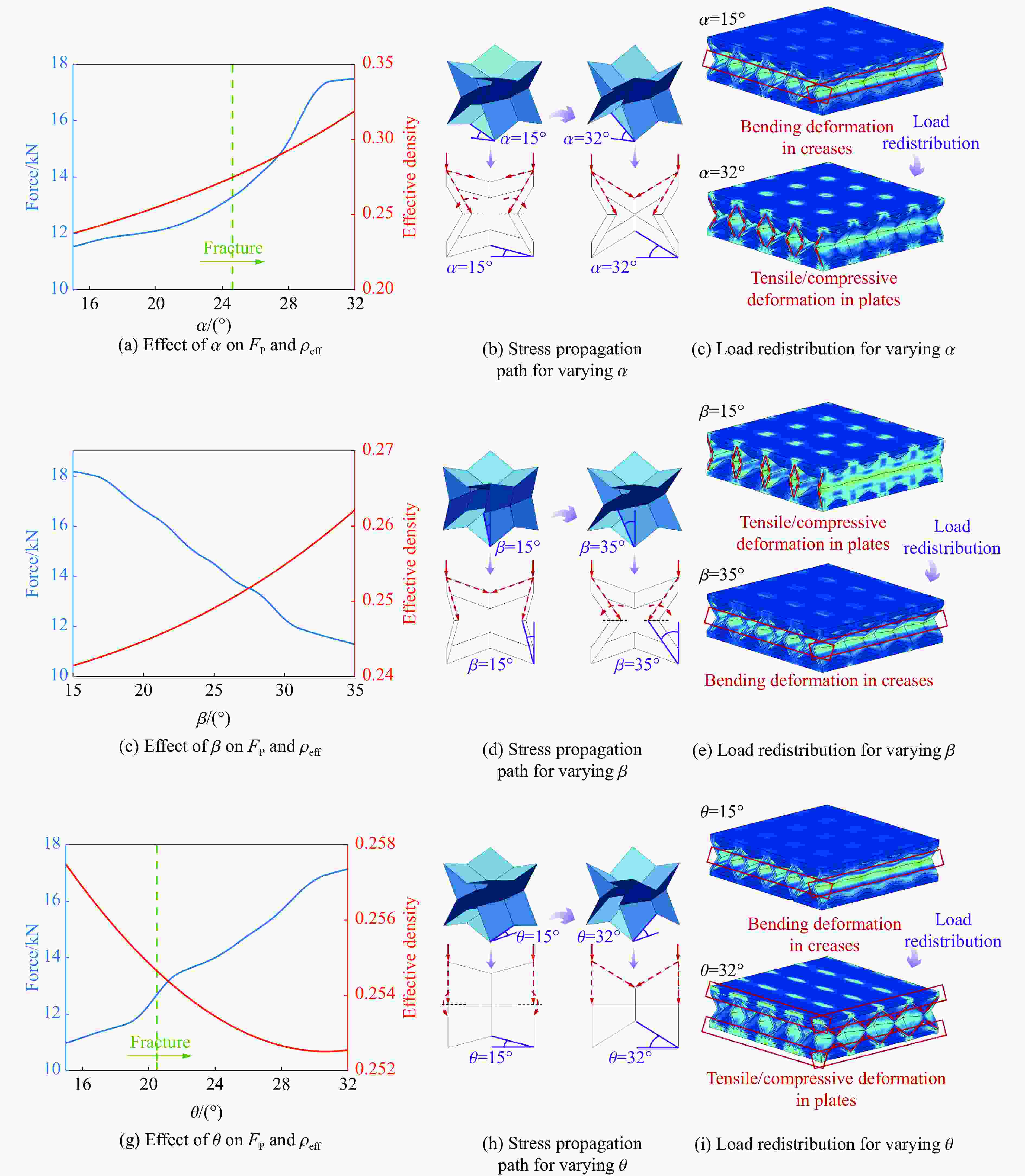
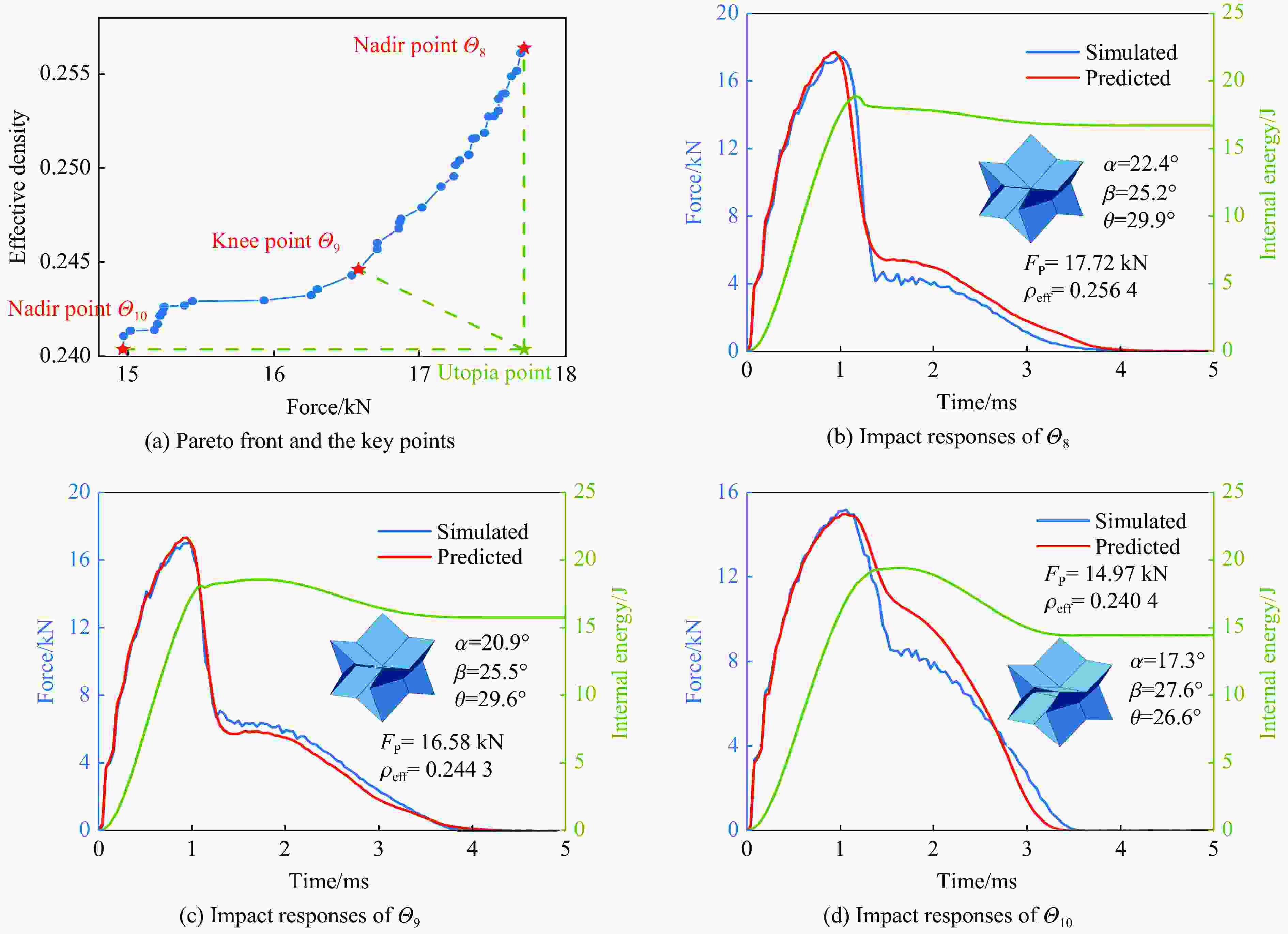
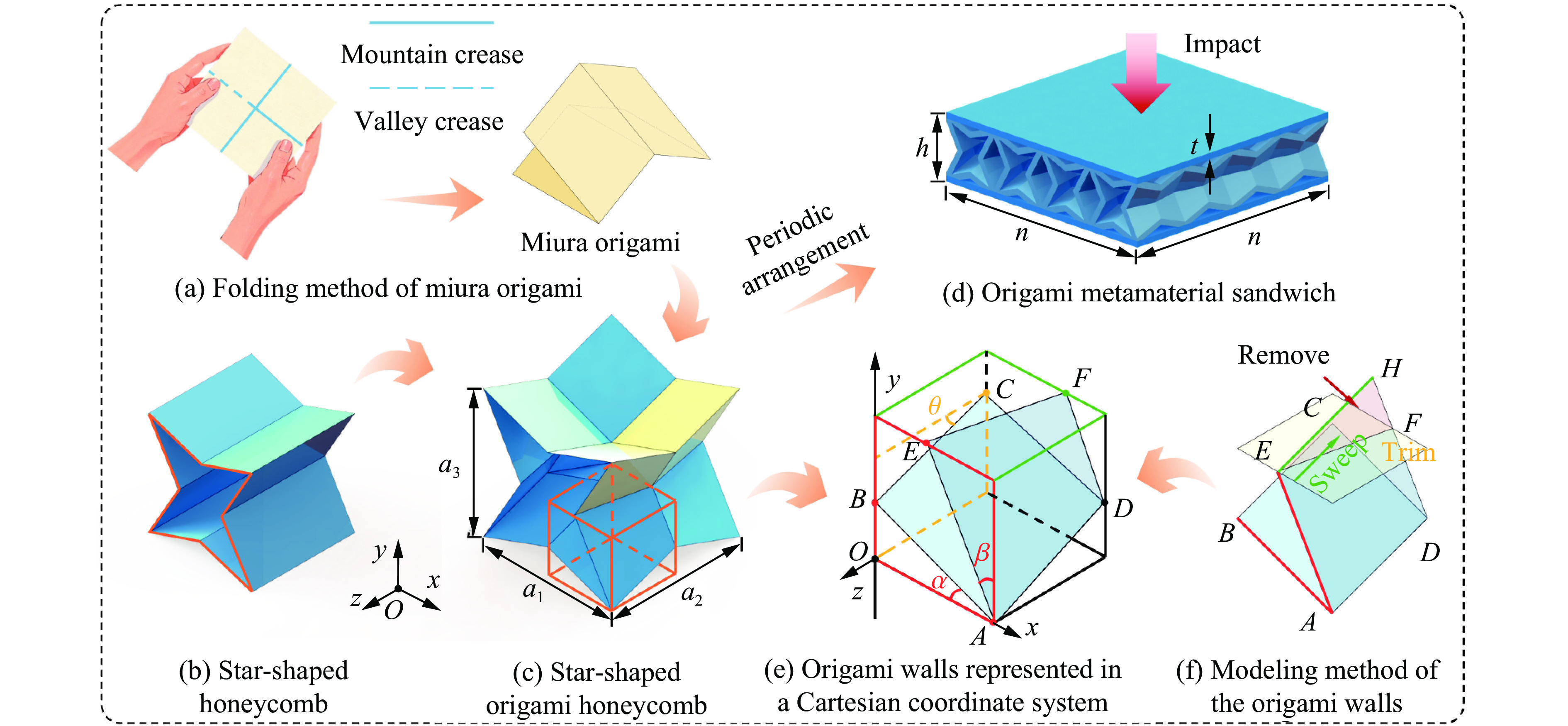
摘要: 受三浦折纸和星形蜂窝的混杂拓扑设计启发，提出了一种新型折纸超材料夹芯复合结构，并融合机器学习实现了其低速冲击响应的预测和多目标优化。通过落锤冲击实验和有限元仿真，系统探究了该结构在低速冲击下的动态力学响应和变形失效模式。结果表明，折纸启发的拓扑结构有效地将传统蜂窝结构的瞬时完全断裂转化为了渐进压溃失效，从而显著提升了其抗冲击性能。随后提出了残差连接增强的深度学习模型，实现了对该结构完整低速冲击响应的快速精确端到端预测，计算效率较有限元仿真大幅提升。并基于此参数分析了关键角度对冲击响应和等效密度的调控机理，特别是角度变化诱导的壁板拉压变形与折痕弯曲变形间的载荷重新分布现象，使结构能在承载型与缓冲型功能间切换，提供了冲击响应与失效模式主动可调控的机理依据。最后，进一步结合强化学习和帕累托前沿分析，以训练完备的深度学习模型作为代理模型，针对承载防护和缓冲防护需求实现了结构的轻量化多目标优化。在等效密度相近时，折纸超材料能够实现峰值力的大范围调控，有益于针对不同防护场景按需定制化开发的防护结构。Abstract: Inspired by the hybrid topology design that integrates Miura origami and star-shaped honeycomb, this study proposes a novel origami metamaterial sandwich and employs machine learning to predict low-velocity impact response and perform multi-objective optimization. Through drop-weight impact experiments and finite element simulations, the dynamic mechanical response and deformation failure modes of the sandwich under low-velocity impact are systematically investigated. The results demonstrate that the origami-inspired topologies effectively transform the instantaneous complete fracture of traditional honeycombs into progressive crushing failure, thereby significantly enhancing impact resistance. Subsequently, a residual connection-enhanced deep learning model is developed, enabling rapid and precise end-to-end prediction of the complete low-velocity impact response, with computational efficiency substantially surpassing that of finite element simulations. Parameterized analysis based on this model reveals the regulatory mechanisms of key angle parameters on impact response and effective density. Particularly, angle variations induce a load redistribution phenomenon between panel tension-compression deformation and crease bending deformation, allowing the metamaterial to switch between bearing and buffering protective functions. This provides a mechanism basis for actively controlling impact response and failure modes. Furthermore, by integrating reinforcement learning and Pareto front analysis, the trained deep learning model served as a surrogate model to achieve lightweight multi-objective optimization tailored for load-bearing and impact-mitigation protection requirements. At similar effective densities, the metamaterial enables broad-range tuning of peak force, offering significant advantages for developing customized protective structures for diverse scenarios. This research not only establishes a solid foundation for creating customizable high-performance impact protection structures but also advances the field toward a new paradigm of intelligent, on-demand design.
-
图 2 实验、有限元仿真及3D打印试件示意图
Figure 2. Schematic of the experiment, the finite element simulation, and the 3D printed specimens
图 3 超材料夹芯复合结构的低速冲击响应
Figure 3. Comparison of low-velocity impact response of metamaterial sandwiches
图 4 超材料夹芯复合结构的失效破坏模式对比
Figure 4. Comparison of failure modes of metamaterial sandwiches
图 8 使用ResANN对折纸超材料夹芯复合结构冲击响应预测的结果
Figure 8. Results of impact response prediction of origami metamaterial sandwiches using ResANN
图 9 关键角度对夹芯复合结构冲击响应和力学属性的影响
Figure 9. Effects of key angles on impact response and mechanical properties of sandwiches
图 10 结合Q-learning和帕累托前沿分析的多目标优化框架。
Figure 10. Multi-objective optimization framework combining Q-learning and Pareto front analysis.
图 11 结合帕累托前沿分析的多目标Q-learning训练过程伪代码。
Figure 11. Pseudocode of the multi-objective Q-learning training process combined with Pareto front analysis.
图 12 承载-轻量化多目标优化结果示意图。
Figure 12. Results of the multi-objective optimization of load-bearing and lightweight.
图 13 缓冲-轻量化多目标优化结果示意图。
Figure 13. Results of the multi-objective optimization of buffering and lightweight.
图 14 折纸超材料芯层变形模式示意图。
Figure 14. Schematic of the deformation mode of the origami metamaterial cores
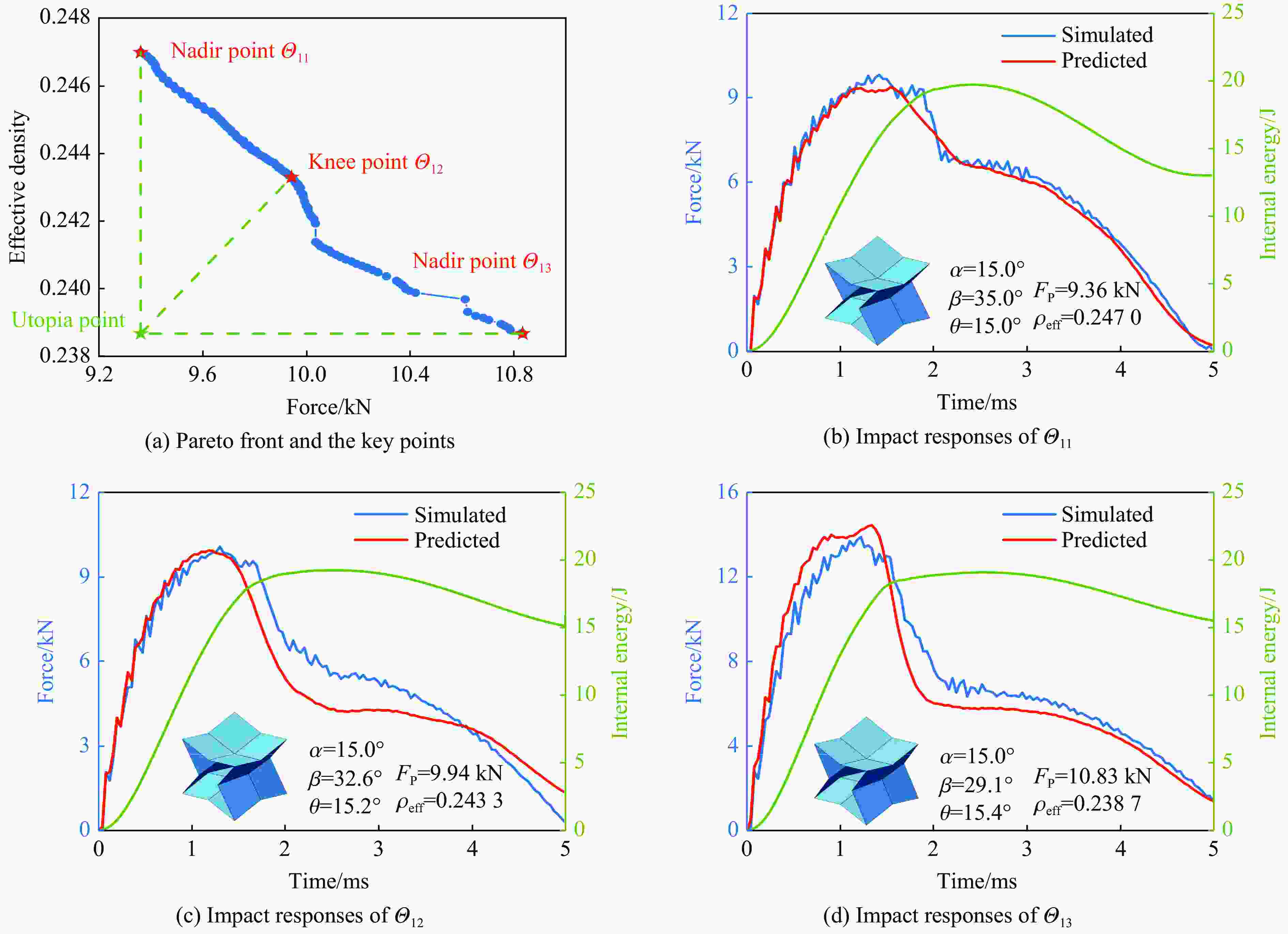
参考点 x坐标 y坐标 z坐标 A a 0 0 B 0 a tan α 0 C 0 a tan α+a tan θ −a D a a tan θ −a E a−a tan β a 0 F a−(a−a tan θ) tan β a −a 
下载: 导出CSV
表 2 折纸超材料夹芯复合结构低速冲击响应及破坏模式对比
Table 2. Comparison of low-velocity impact response and failure modes of origami metamaterial sandwiches
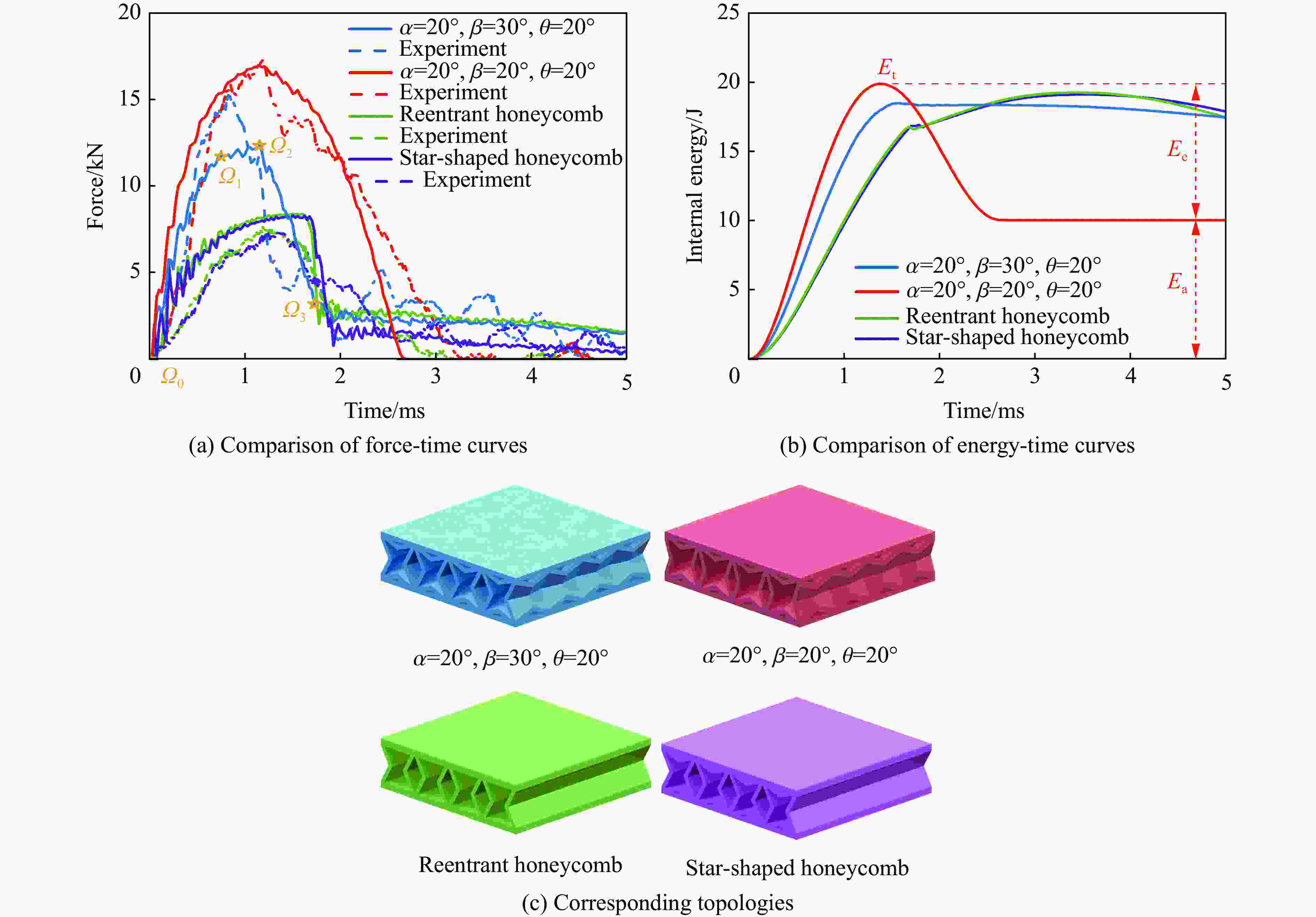
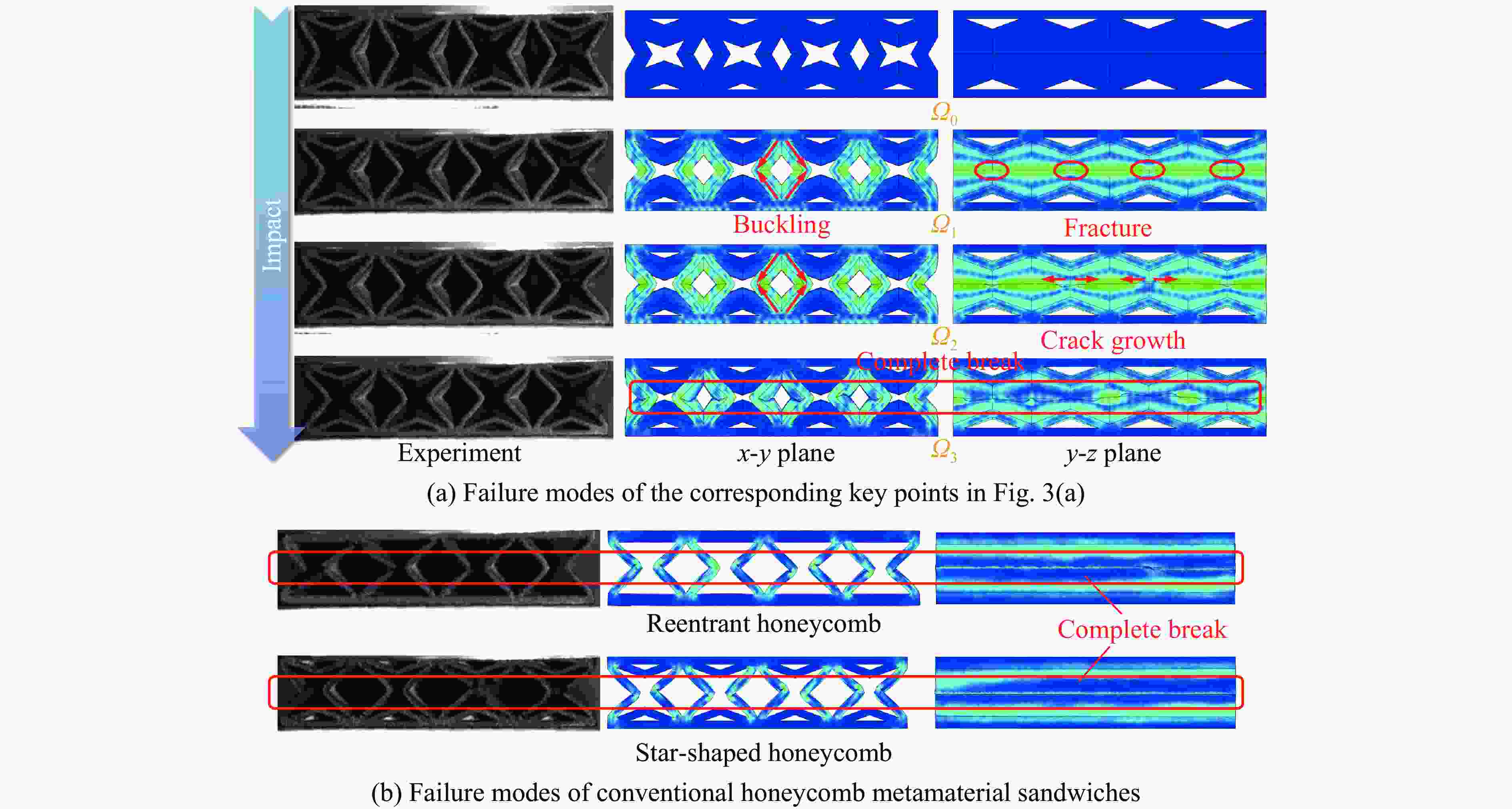
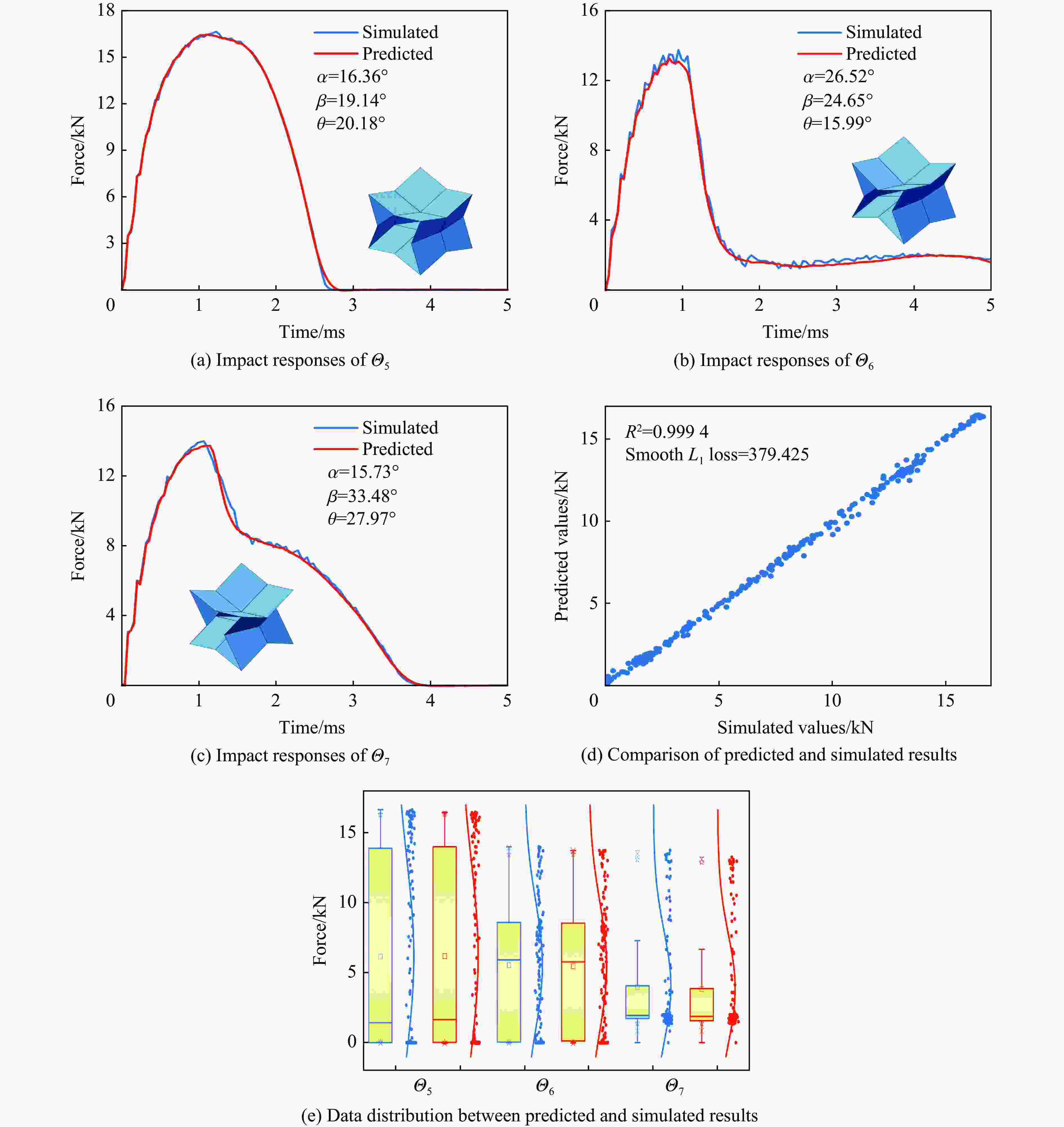
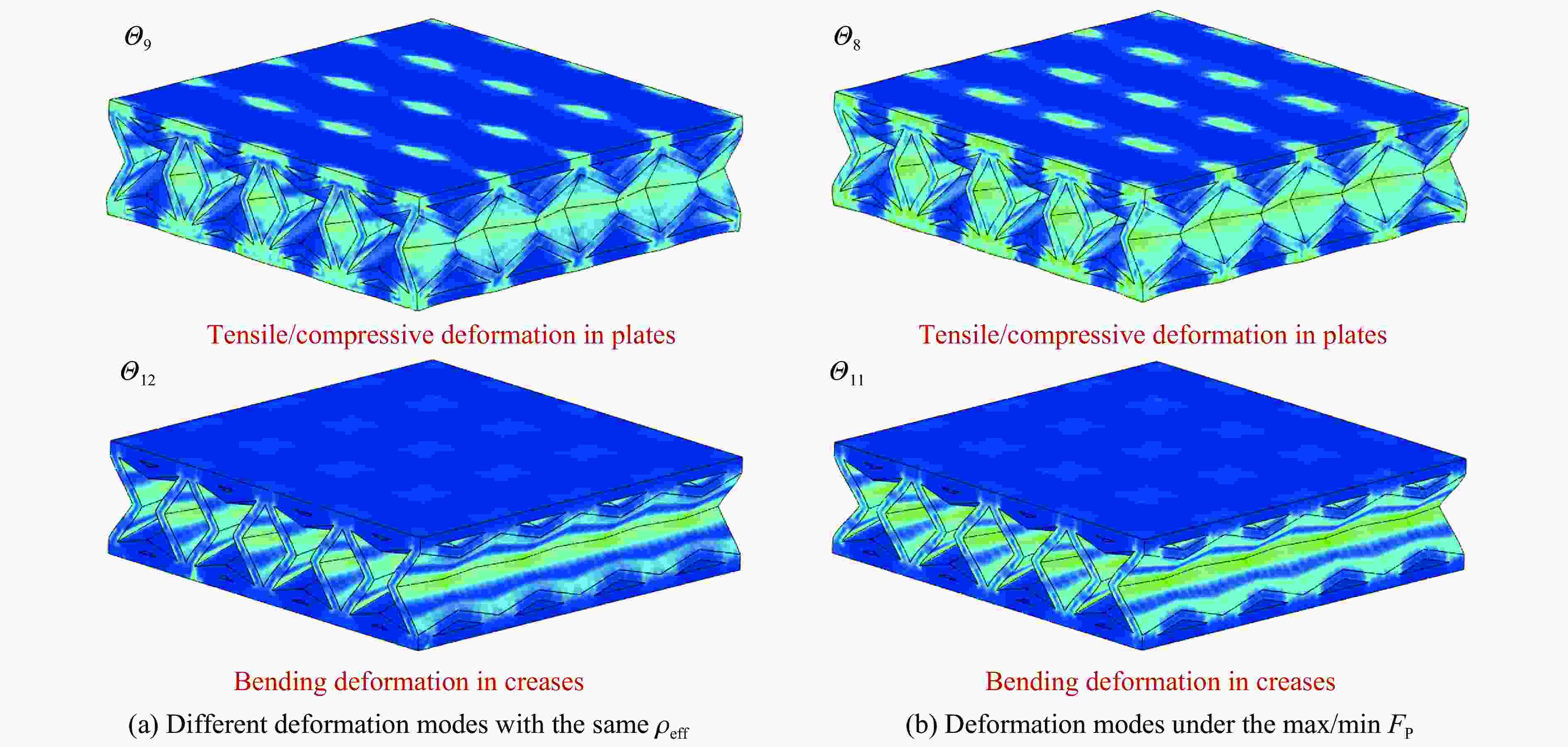
超材料夹芯复合结构 FP/kN tP/ms Ea/J ρeff 破坏模式 Θ1 α=20°, β=20°, θ=20° 16.97 2.70 10.04 0.2447 未破坏 Θ2 α=20°, β=30°, θ=20° 12.34 1.93 17.44 0.2549 折痕渐进压溃 Θ3 内凹蜂窝 8.43 2.05 17.43 0.2155 瞬时完全断裂 Θ4 星形蜂窝 8.32 1.93 17.87 0.2713 瞬时完全断裂
下载: 导出CSV
表 3 多类神经网络模型的性能对比
Table 3. Performance comparison of various types of neural network models
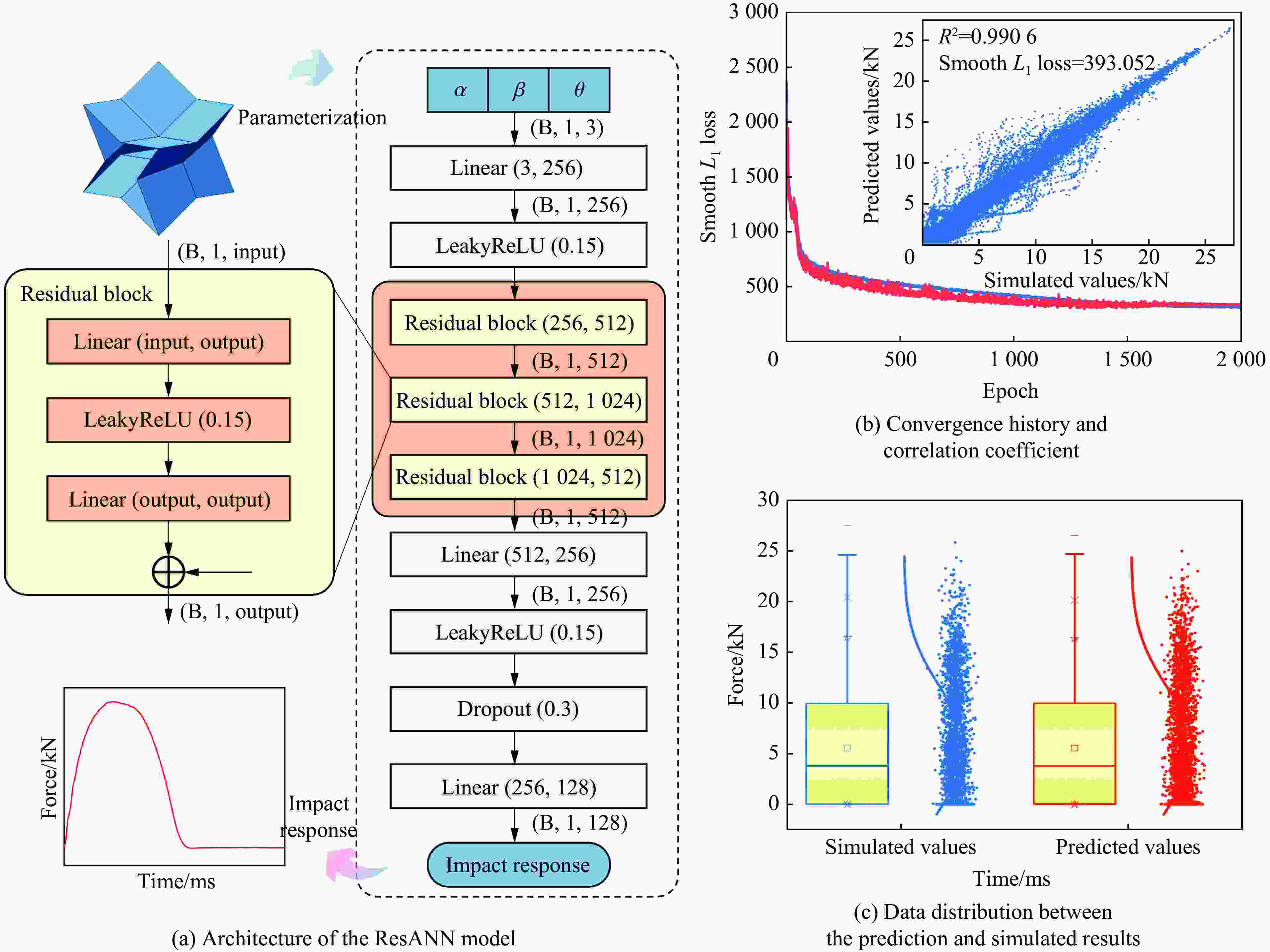
神经网络模型 参数量 训练时间/s 预测时间/s Smooth L1 loss R2 ResANN 4103552 2146.46 2.14 393.052 0.9906 ANN 3972480 2004.74 2.47 463.131 0.9880 CNN 3973472 1961.79 3.32 1886.84 0.8850 LSTM 4245632 1609.75 2.73 1837.11 0.8894
下载: 导出CSV
表 4 多目标Q-learning优化模型所使用的Q表
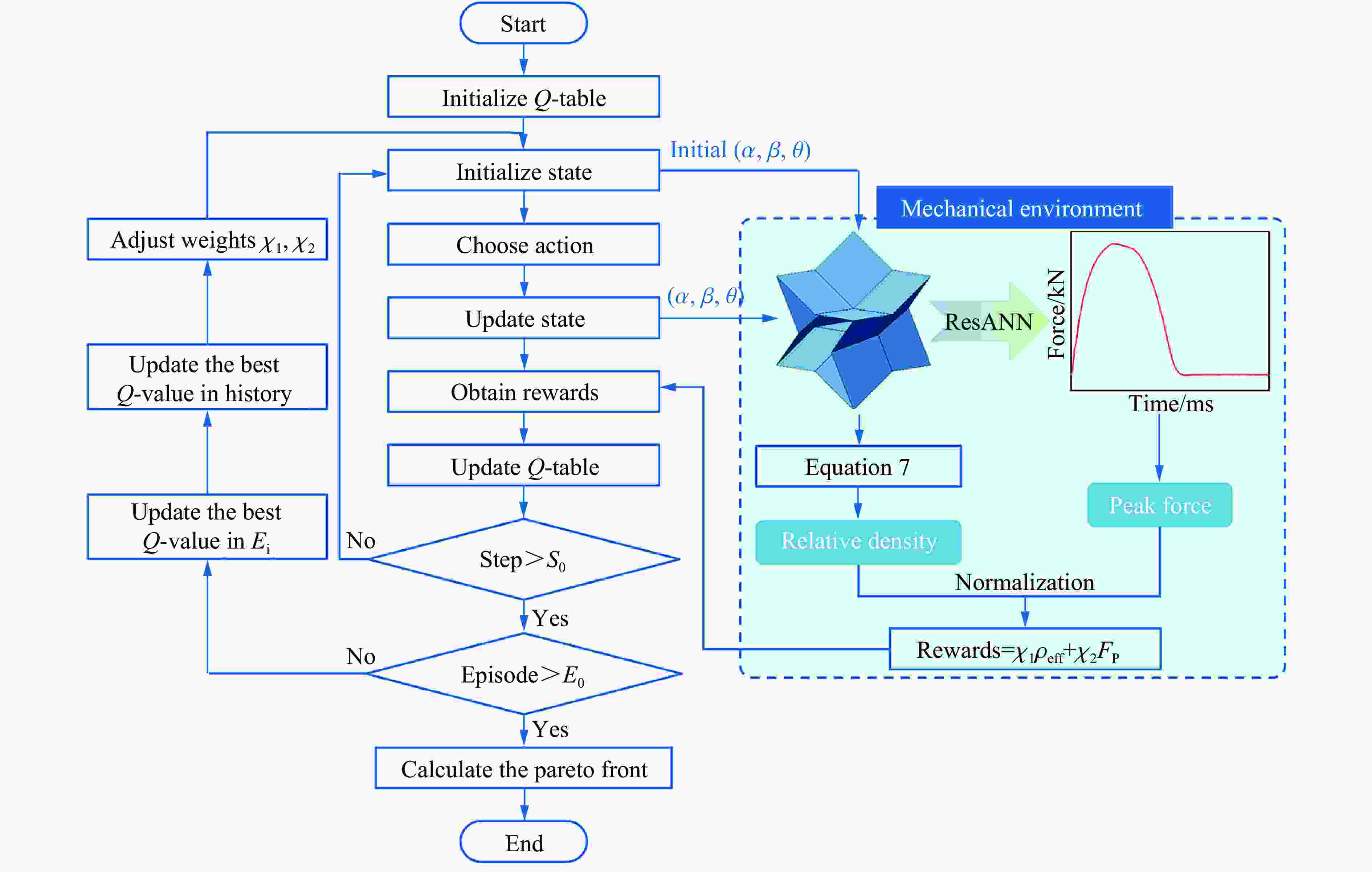
Table 4. The Q-table used in the multi-objective Q-learning optimization model
S=(α, β, θ) A1 A2 … A7 S1 Q(S1, A1) Q(S1, A2) … Q(S1, A7) S2 Q(S2, A1) Q(S2, A2) … Q(S2, A7) … … … … …
下载: 导出CSV
-
[1] 敬霖, 王志华, 赵隆茂. 多孔金属及其夹芯结构力学性能的研究进展 [J]. 力学与实践, 2015, 37(1): 1–24,48. DOI: 10.6052/1000-0879-14-180.JING L, WANG Z H, ZHAO L M. Advances in studies of the mechanical performance of cellular metals and related sandwich structures [J]. Mechanics in Engineering, 2015, 37(1): 1–24,48. DOI: 10.6052/1000-0879-14-180. [2] 崔天宁, 秦庆华. 轻质多孔夹芯结构的弹道侵彻行为研究进展 [J]. 力学进展, 2023, 53(2): 395–432. DOI: 10.6052/1000-0992-23-002.CUI T N, QIN Q H. Ballistic performance of lightweight cellular sandwich structures: a review [J]. Advances in Mechanics, 2023, 53(2): 395–432. DOI: 10.6052/1000-0992-23-002. [3] 余同希, 朱凌, 许骏. 结构冲击动力学进展(2010-2020) [J]. 爆炸与冲击, 2021, 41(12): 121401. DOI: 10.11883/bzycj-2021-0113.YU T X, ZHU L, XU J. Progress in structural impact dynamics during 2010−2020 [J]. Explosion and Shock Waves, 2021, 41(12): 121401. DOI: 10.11883/bzycj-2021-0113. [4] 张元瑞, 朱玉东, 王克鸿, 等. 多胞子弹冲击泡沫夹芯梁的动力学响应分析 [J]. 爆炸与冲击, 2024, 44(9): 091442. DOI: 10.11883/bzycj-2024-0045.ZHANG Y R, ZHU Y D, WANG K H, et al. Dynamic response analysis of cellular projectile impacting foam sandwich beam [J]. Explosion and Shock Waves, 2024, 44(9): 091442. DOI: 10.11883/bzycj-2024-0045. [5] 苏兴亚, 敬霖, 赵隆茂. 爆炸载荷下分层梯度泡沫铝夹芯板的失效模式与抗冲击性能 [J]. 爆炸与冲击, 2019, 39(6): 063103. DOI: 10.11883/bzycj-2018-0198.SU X Y, JING L, ZHAO L M. Failure modes and shock resistance of sandwich panels with layered-gradient aluminum foam cores under air-blast loading [J]. Explosion and Shock Waves, 2019, 39(6): 063103. DOI: 10.11883/bzycj-2018-0198. [6] 李雨薇, 易昶成, 刘志芳, 等. 剪切增稠液填充蜂窝夹芯板的低速冲击响应 [J]. 爆炸与冲击, 2025, 45(1): 013103. DOI: 10.11883/bzycj-2024-0095.LI Y W, YI C C, LIU Z F, et al. Low-velocity impact responses of shear-thickening fluid-filled honeycomb sandwich structures [J]. Explosion and Shock Waves, 2025, 45(1): 013103. DOI: 10.11883/bzycj-2024-0095. [7] 于相龙, 周济. 力学超材料的构筑及其超常新功能 [J]. 中国材料进展, 2019, 38(1): 14–21. DOI: 10.7502/j.issn.1674-3962.2019.01.02.YU X L, ZHOU J. Mechanical metamaterials: architected materials and unexplored properties [J]. Materials China, 2019, 38(1): 14–21. DOI: 10.7502/j.issn.1674-3962.2019.01.02. [8] 张栗铭, 杨德庆. 力学与声学超材料在船舶工程中的应用研究综述 [J]. 中国舰船研究, 2023, 18(2): 1–19,47. DOI: 10.19693/j.issn.1673-3185.03139.ZHANG L M, YANG D Q. Review on the applied research of mechanical and acoustic metamaterials in ship engineering [J]. Chinese Journal of Ship Research, 2023, 18(2): 1–19,47. DOI: 10.19693/j.issn.1673-3185.03139. [9] CHEN C Q, HE Y L, XU R, et al. Dynamic behaviors of sandwich panels with 3D-printed gradient auxetic cores subjected to blast load [J]. International Journal of Impact Engineering, 2024, 188: 104943. DOI: 10.1016/j.ijimpeng.2024.104943. [10] JIANG Z F, RONG J L, CHEN Z C, et al. Deformation mechanisms and energy absorption characteristics of 3D-printed negative Poisson's ratio sandwich structures subjected to underwater impulsive loading [J]. International Journal of Impact Engineering, 2025, 203: 105355. DOI: 10.1016/j.ijimpeng.2025.105355. [11] 方虹斌, 吴海平, 刘作林, 等. 折纸结构和折纸超材料动力学研究进展 [J]. 力学学报, 2022, 54(1): 1–38. DOI: 10.6052/0459-1879-21-478.FANG H B, WU H P, LIU Z L, et al. Advances in the dynamics of origami structures and origami metamaterials [J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(1): 1–38. DOI: 10.6052/0459-1879-21-478. [12] 岳晓奎, 朱明珠, 耿浩华, 等. 折纸超材料及其在航空航天领域的应用与展望 [J]. 航空学报, 2025, 46(6): 531382. DOI: 10.7527/S1000-6893.2024.31382.YUE X K, ZHU M Z, GENG H H, et al. Origami metamaterials and their applications and prospects in aerospace field [J]. Acta Aeronautica et Astronautica Sinica, 2025, 46(6): 531382. DOI: 10.7527/S1000-6893.2024.31382. [13] HE Y L, ZHANG P W, YOU Z, et al. Programming mechanical metamaterials using origami tessellations [J]. Composites Science and Technology, 2020, 189: 108015. DOI: 10.1016/j.compscitech.2020.108015. [14] HE Y L, CHEN C Q, SUN J P, et al. Deformation and failure of 3D-Printed origami-inspired sandwich beam under blast loading [J]. International Journal of Impact Engineering, 2025, 206: 105471. DOI: 10.1016/j.ijimpeng.2025.105471. [15] 何远鹏, 王凌峰, 杨秋松, 等. 多折角梯形台面折纸夹层结构的冲击防护性能 [J]. 爆炸与冲击, 2024, 44(4): 043103. DOI: 10.11883/bzycj-2023-0315.HE Y P, WANG L F, YANG Q S, et al. Impact response of TPS folded sandwich structure [J]. Explosion and Shock Waves, 2024, 44(4): 043103. DOI: 10.11883/bzycj-2023-0315. [16] ZHANG J J, LU G X, ZHANG Y, et al. A study on ballistic performance of origami sandwich panels [J]. International Journal of Impact Engineering, 2021, 156: 103925. DOI: 10.1016/j.ijimpeng.2021.103925. [17] QI J Q, LI C, TIE Y, et al. Energy absorption characteristics of origami-inspired honeycomb sandwich structures under low-velocity impact loading [J]. Materials & Design, 2021, 207: 109837. DOI: 10.1016/j.matdes.2021.109837. [18] 代铁琳, 金刘超, 尚宸, 等. 超材料的智能设计研究进展 [J]. 计算机辅助设计与图形学学报, 2025, 37(1): 1–27. DOI: 10.3724/SP.J.1089.2024-00279.DAI T L, JIN L C, SHANG C, et al. Advances in intelligent design of metamaterials [J]. Journal of Computer-Aided Design & Computer Graphics, 2025, 37(1): 1–27. DOI: 10.3724/SP.J.1089.2024-00279. [19] 王清华, 徐丰, 郭伟国. 基于ANN-GA协同寻优的动态拉伸试样尺寸优化方法 [J]. 爆炸与冲击, 2022, 42(1): 014201. DOI: 10.11883/bzycj-2021-0218.WANG Q H, XU F, GUO W G. A method of geometry optimization for dynamic tensile specimen based on artificial neural network and genetic algorithm [J]. Explosion and Shock Waves, 2022, 42(1): 014201. DOI: 10.11883/bzycj-2021-0218. [20] XIAO L J, SHI G Q, SONG W D. Machine learning predictions on the compressive stress-strain response of lattice-based metamaterials [J]. International Journal of Solids and Structures, 2024, 300: 112893. DOI: 10.1016/j.ijsolstr.2024.112893. [21] SHEN X Y, HU Q R, ZHU D F, et al. Dynamic mechanical response prediction model of honeycomb structure based on machine learning method and finite element method [J]. International Journal of Impact Engineering, 2024, 184: 104825. DOI: 10.1016/j.ijimpeng.2023.104825. [22] ZHU Z H, KONG X S, ZHOU H, et al. A hybrid data-driven machine learning framework for predicting the impact resistance of composite armor [J]. International Journal of Impact Engineering, 2025, 195: 105125. DOI: 10.1016/j.ijimpeng.2024.105125. [23] BROWN N K, GARLAND A P, FADEL G M, et al. Deep reinforcement learning for the rapid on-demand design of mechanical metamaterials with targeted nonlinear deformation responses [J]. Engineering Applications of Artificial Intelligence, 2023, 126: 106998. DOI: 10.1016/j.engappai.2023.106998. [24] ZHU S W, CHEN H, YANG X Q, et al. Rubik’s cube as in-situ programmable matter and a reconfigurable mechanical metamaterial [J]. Science China Technological Sciences, 2024, 67(10): 3221–3234. DOI: 10.1007/s11431-024-2681-1. [25] ZHENG H K, LI C L, SUN Y, et al. Impact protection mechanism and failure prediction of modular hierarchical honeycomb system with self-locking effect [J]. International Journal of Impact Engineering, 2025, 201: 105274. DOI: 10.1016/j.ijimpeng.2025.105274. [26] HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition [C]//Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770-778. DOI: 10.1109/CVPR.2016.90. [27] REN S Q, HE K M, GIRSHICK R, et al. Faster R-CNN: towards real-time object detection with region proposal networks [C]//Proceedings of the 29th International Conference on Neural Information Processing Systems - Volume 1. Montreal: MIT Press, 2015: 91-99. DOI: 10.5555/2969239.2969250. [28] LOSHCHILOV I, HUTTER F. Decoupled weight decay regularization[J]. ArXiv Preprint, 2017, arXiv: 1711.05101. DOI: 10.48550/arXiv.1711.05101. [29] WATKINS C J C H, DAYAN P. Q-learning [J]. Machine Learning, 1992, 8(3): 279–292. DOI: 10.1007/BF00992698. [30] HAN S H, LI C L, HAN Q, et al. Machine learning-aided prediction and customization on mechanical response and wave attenuation of multifunctional kiri/origami metamaterials [J]. Extreme Mechanics Letters, 2025, 74: 102276. DOI: 10.1016/j.eml.2024.102276. -
计量
- 文章访问数: 236
- HTML全文浏览量: 29
- PDF下载量: 81
- 被引次数: 0