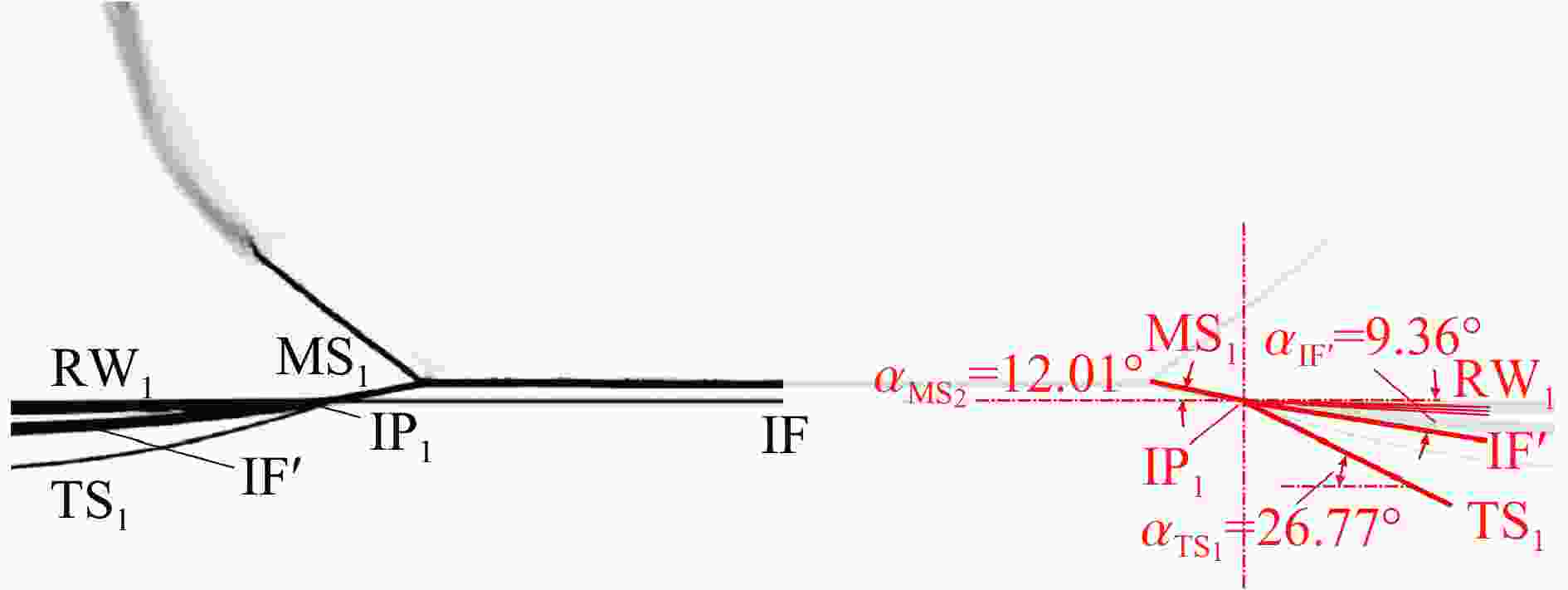马赫反射波系在平面重/轻界面的入射加载

郭景琪; 鲁怡展; 张恩来; 邹立勇

doi:10.11883/bzycj-2025-0465

马赫反射波系在平面重/轻界面的入射加载

doi: 10.11883/bzycj-2025-0465

中国工程物理研究院流体物理研究所冲击波物理与爆轰物理全国重点实验室，四川绵阳 621999

基金项目: 国家自然科学基金（12472397，92052108）；冲击波物理与爆轰物理全国重点实验室基金(2023JCJQLB05402，JCKYS2023212003)

详细信息

作者简介:
郭景琪（2001－　），男，博士研究生，guojingqi23@gscaep.ac.cn

通讯作者:
邹立勇（1975－　），男，博士，研究员，zly@caep.cn

中图分类号: O354.5
计量
- 文章访问数: 168
- HTML全文浏览量: 21
- PDF下载量: 25
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-27
- 修回日期: 2025-09-01
- 网络出版日期: 2025-09-04

Incident impact of Mach reflection wave configuration at a planar heavy/light interface

National Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China

摘要

摘要: 采用数值模拟与理论分析相结合的方法，研究了马赫反射波系与平面SF₆/N₂界面的作用过程，特别关注其中马赫反射波系的入射加载阶段。在入射平面激波马赫数为1.8的情况下，给出了绕刚体圆柱后形成马赫反射波系的数值纹影，定性分析了马赫反射波系入射加载重/轻界面的波系演化过程。运用三激波理论对折射过程进行分析求解，结果表明该理论解可以良好预测折射后的激波形态以及界面上的环量沉积和速度扰动。进一步，通过绘制激波极曲线和稀疏波特征线，直观描述了入射加载过程中波系前后的压力变化和气流偏转。理论分析和数值模拟结果均表明，马赫反射波系中激波强度以及入射角的差异诱导了界面上的纵向速度扰动，激波加载带来的切向速度诱导了界面上的环量沉积，速度扰动和环量主导了重/轻界面前期的演化。
- Richtmyer-Meshkov不稳定性 /
- 马赫反射波系 /
- 重/轻界面 /
- 三激波理论
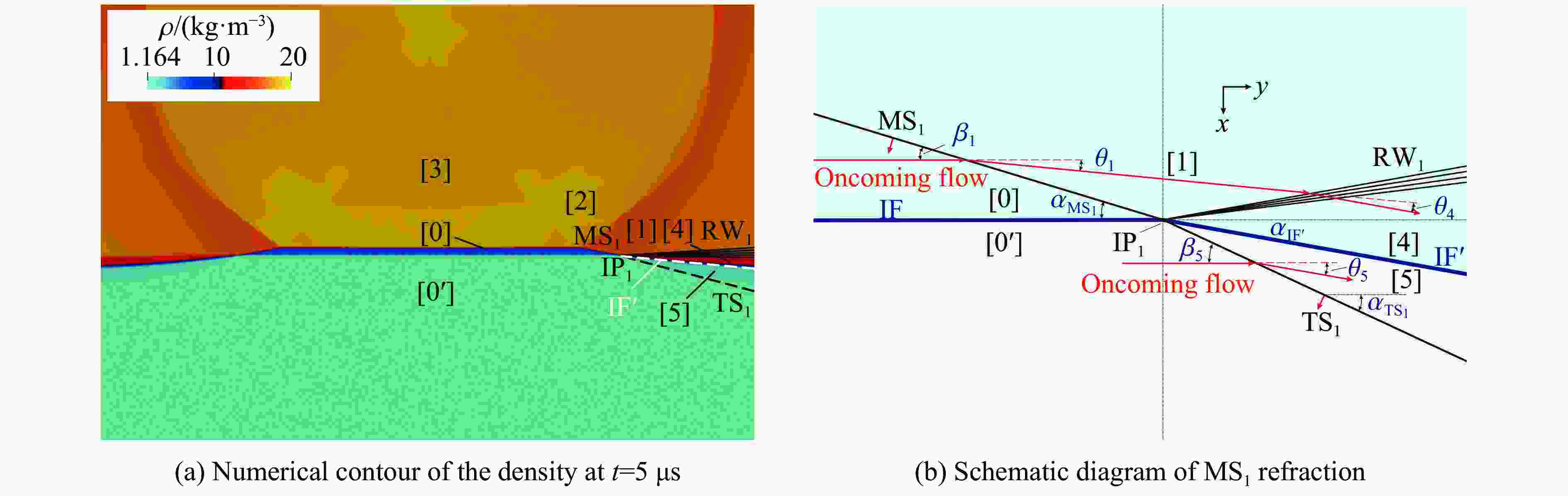
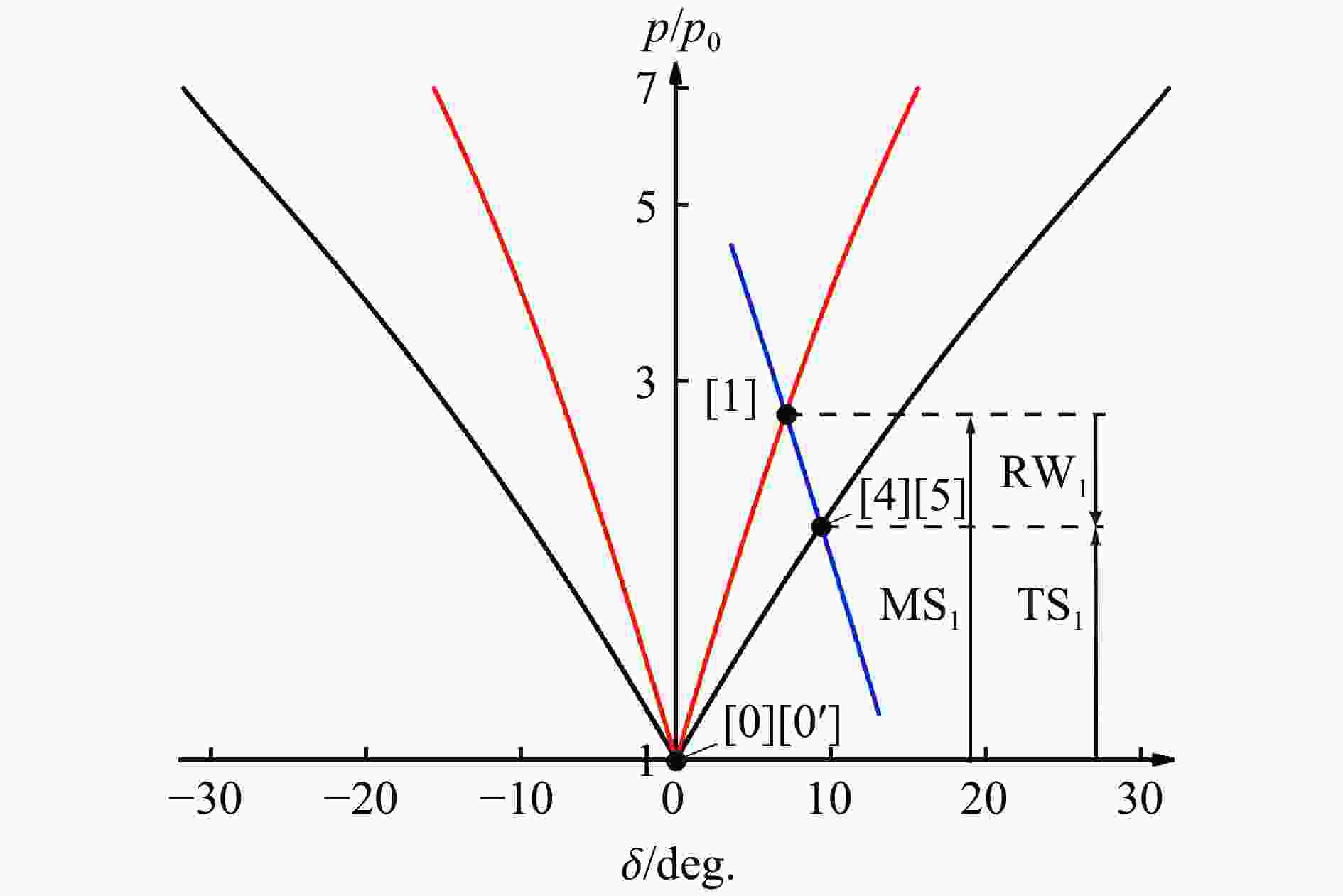
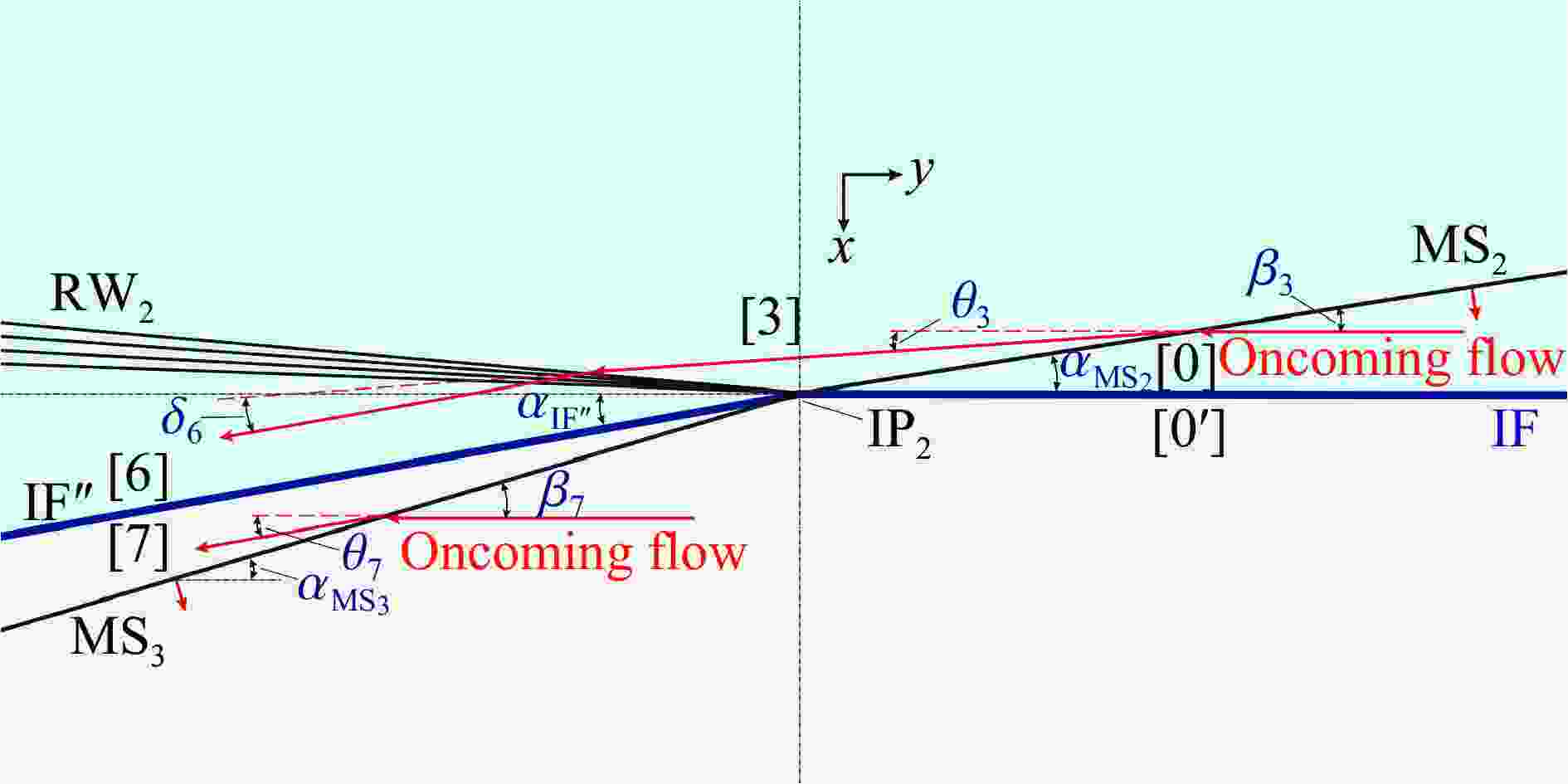
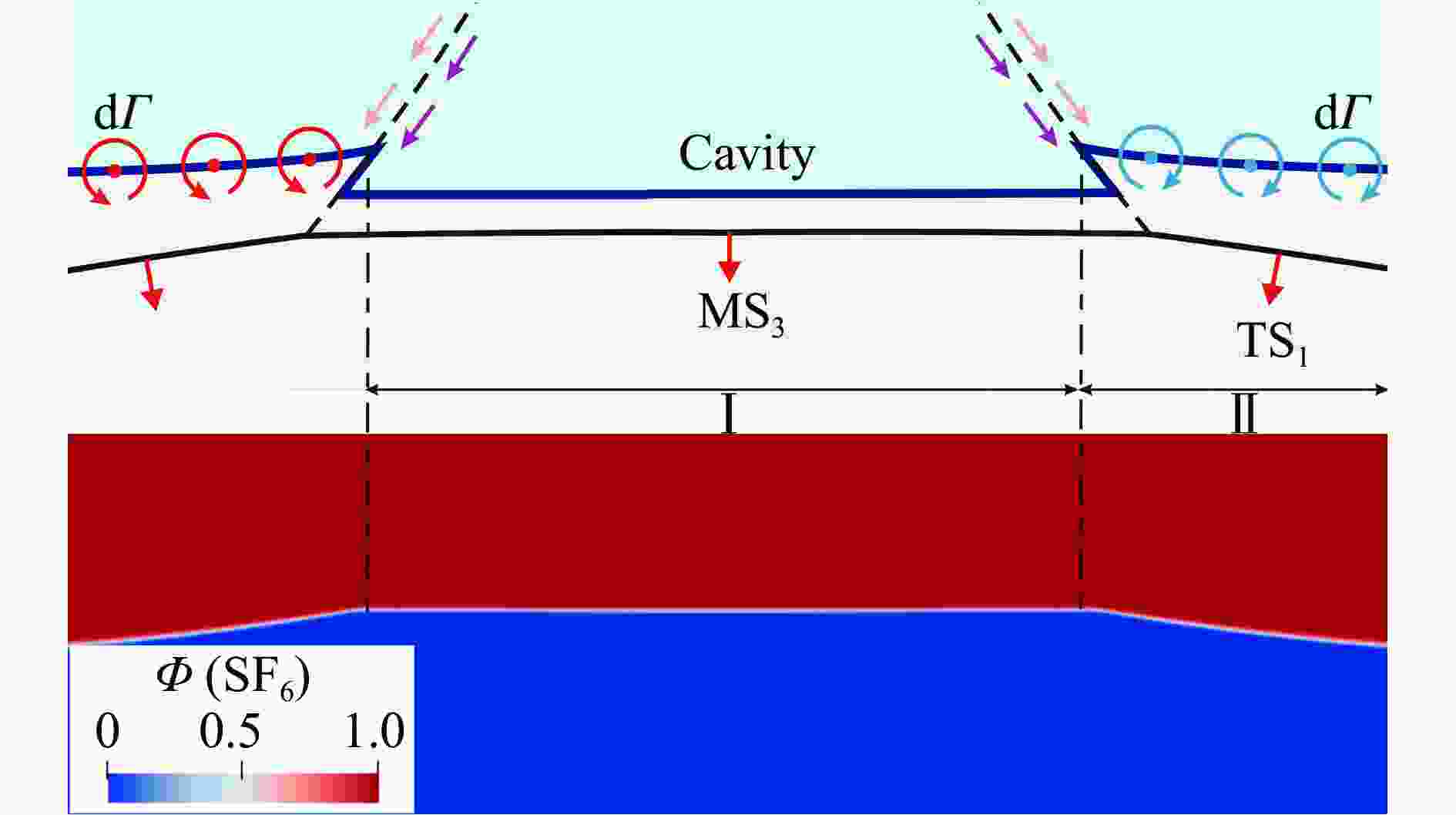
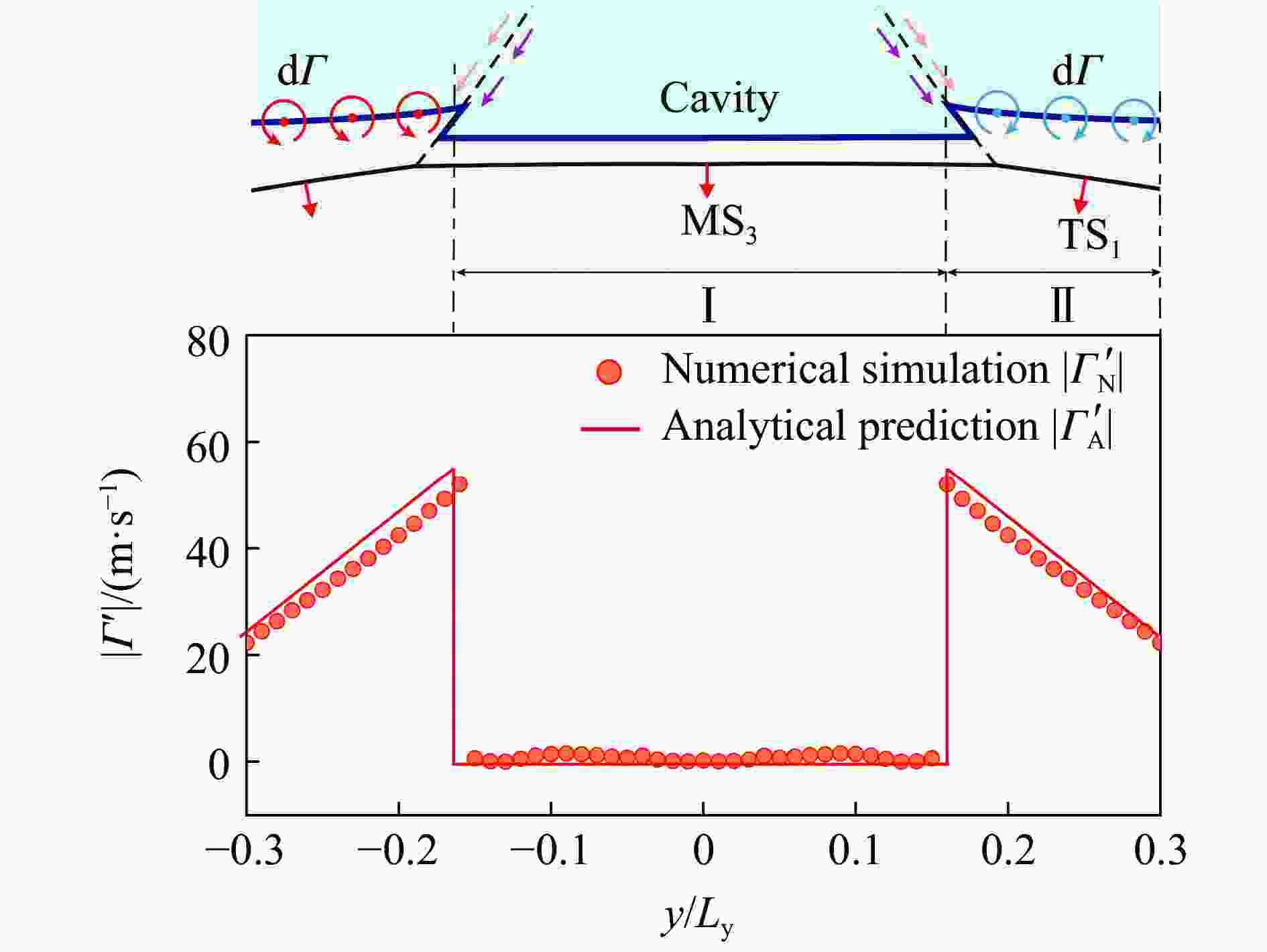
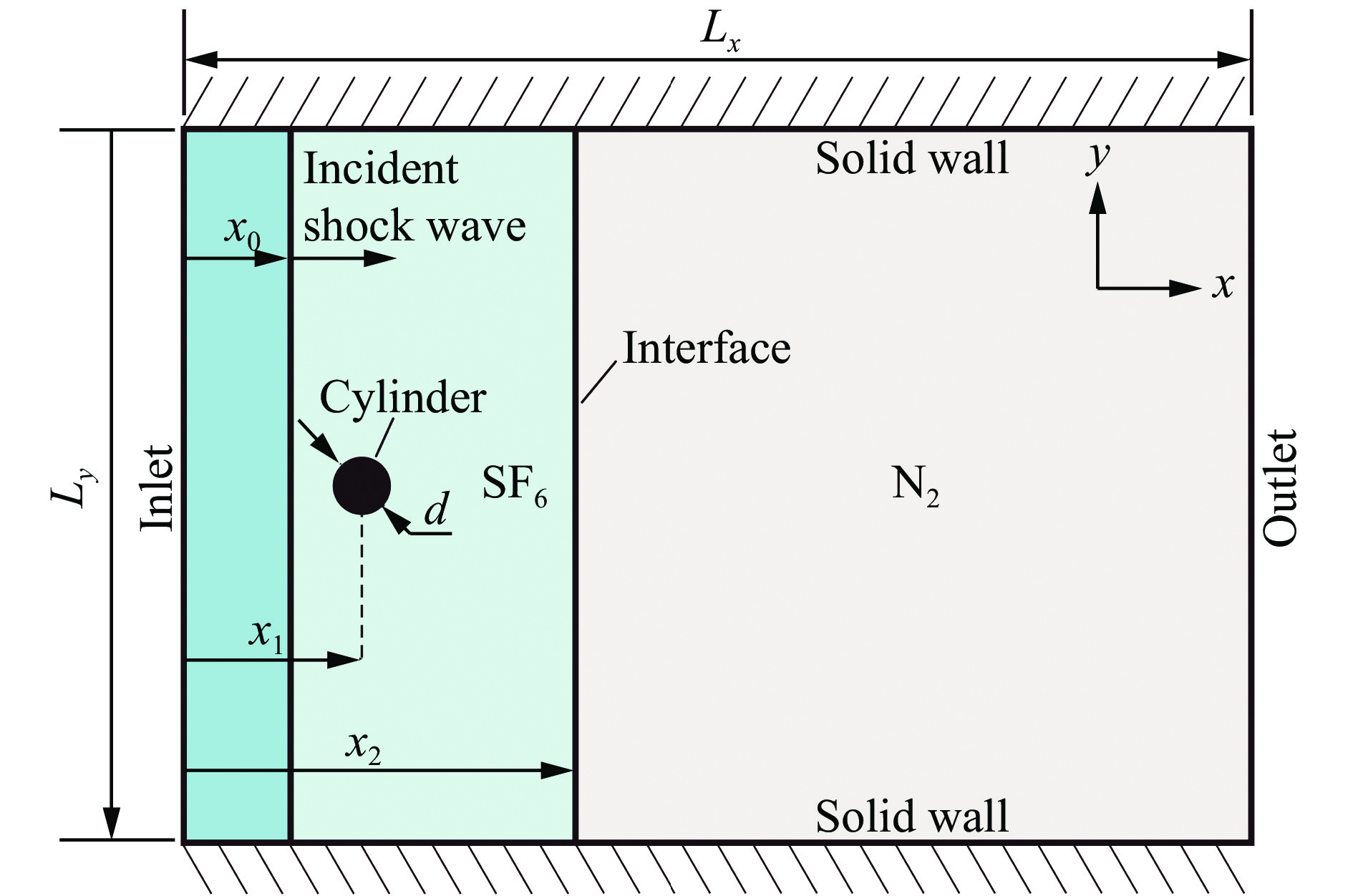
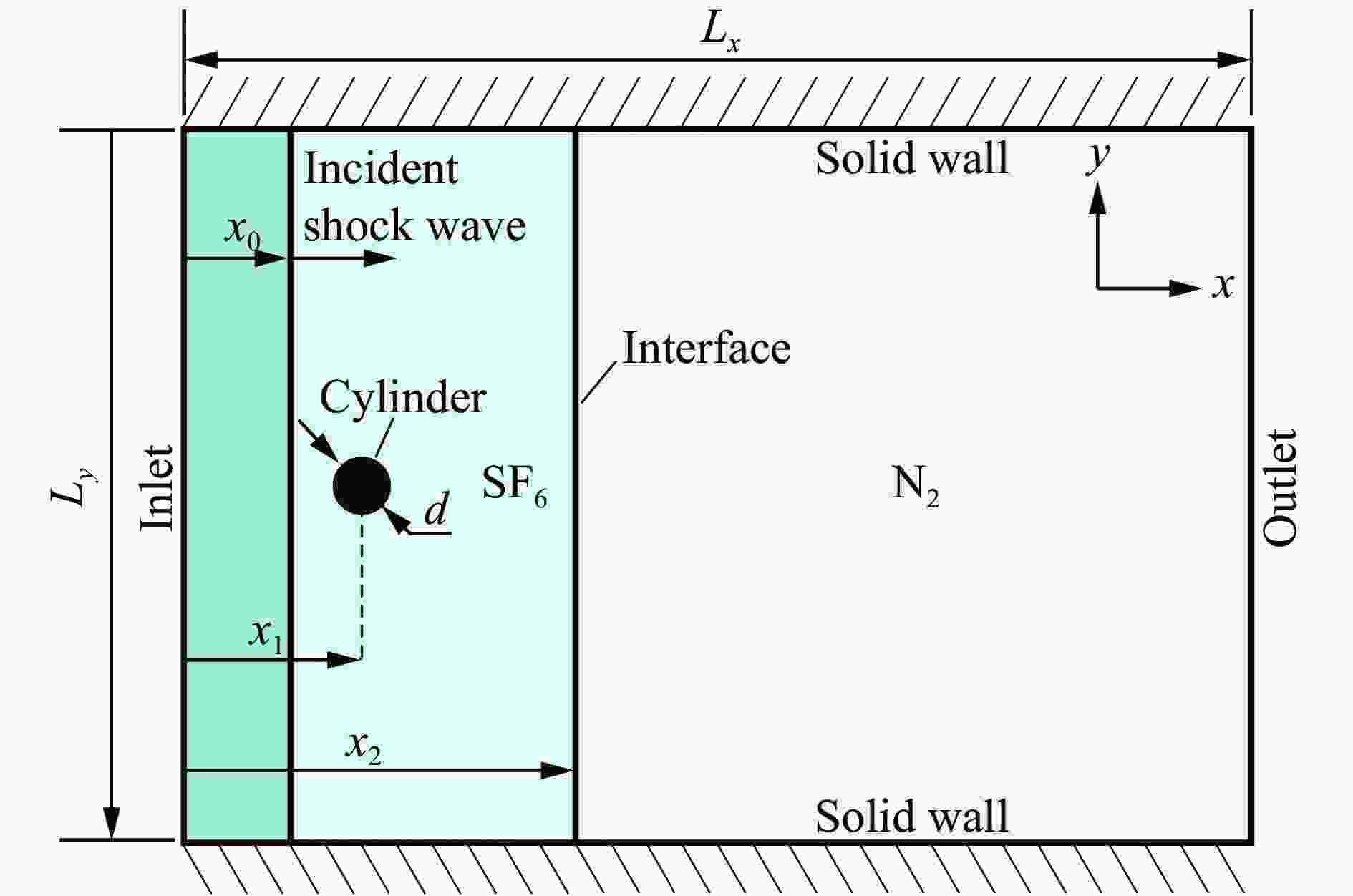
Abstract: The evolution of a planar heavy/light gas interface (SF₆/N₂) subjected to a perturbed shock wave produced by diffracting a planar incident shock over a rigid cylinder is investigated by numerical and theoretical analysis, particularly focusing on the incident impact stage of Mach reflection wave configuration. While the Mach number of incident planar shock wave is 1.8, numerical schlieren images of the Mach reflection wave over a rigid cylinder are provided, and the wave evolution during the incident impact on the heavy/light interface is quantitatively analyzed. Utilizing the three-shock theory, an analytical solution describing the refraction process is derived, which accurately predicts the post-refraction shock wave shape, as well as the velocity perturbation and circulation deposition on the interface. Additionally, by drawing shock polar curves and rarefaction wave characteristic lines, the pressure changes and flow deflection across the wave configuration during the incident impact process are straightly described. Both the results of theoretical analysis and numerical simulation indicate that the differences in shock intensity and incident angles within the Mach reflection wave configuration lead to the velocity perturbation on the interface. And the tangential velocity caused by the shock impact results in circulation deposition on the interface. Velocity perturbation and circulation deposition dominate the early evolution of the heavy/light interface.
- Richtmyer-Meshkov instability /
- Mach reflection wave configuration /
- heavy/light interface /
- three-shock theory

HTML全文

图 1 计算域示意图

Figure 1. Schematic diagram of the computational domain

下载: 全尺寸图片幻灯片

图 2 t = 150 μs时4种网格尺寸下沿x = 40.5 mm方向的密度曲线

Figure 2. Density curves along x = 40.5 mm with the four grid sizes at t = 150 μs

下载: 全尺寸图片幻灯片

图 3 数值模拟和实验结果对比

Figure 3. Comparison of the numerical and the experimental results

下载: 全尺寸图片幻灯片

图 4 马赫反射波系入射加载平面SF₆/N₂界面过程的数值纹影图

Figure 4. Numerical schlieren visualization of Mach reflection wave configuration at a planar SF₆/N₂ gas interface

下载: 全尺寸图片幻灯片

图 5 马赫反射波系结构的定性描述

Figure 5. Qualitative description of Mach reflection wave configuration

下载: 全尺寸图片幻灯片

图 6 马赫反射波系理论模型与数值模拟结果对比

Figure 6. Comparison of Mach reflection wave configuration between analytical prediction and numerical simulation

下载: 全尺寸图片幻灯片

图 7 马赫反射波系极曲线

Figure 7. Shock-polar solution of Mach reflection wave configuration

下载: 全尺寸图片幻灯片

图 8 马赫杆MS₁在界面折射的定性描述

Figure 8. Qualitative description of the MS₁ refraction

下载: 全尺寸图片幻灯片

图 9 马赫杆MS₁折射的理论模型与数值模拟对比

Figure 9. Comparison of the MS₁ refraction between analytical prediction and numerical simulation

下载: 全尺寸图片幻灯片

图 10 MS₁折射过程极曲线

Figure 10. Shock-polar solution of the the MS₁ refraction

下载: 全尺寸图片幻灯片

图 11 MS₂折射过程示意图

Figure 11. Schematic diagram of MS₂ refraction

下载: 全尺寸图片幻灯片

图 12 马赫反射波系入射加载后的界面

Figure 12. The interface after the incident impact of Mach reflection wave configuration

下载: 全尺寸图片幻灯片

图 13 入射加载后界面环量分布

Figure 13. Circulation deposition after incident impact

下载: 全尺寸图片幻灯片

图 14 入射加载后界面扰动速度分布

Figure 14. Velocity perturbation after incident impact

下载: 全尺寸图片幻灯片

表 1 重/轻气体的初始参数

Table 1. Initial parameters of heavy and light gases

气体	密度ρ/(kg·m⁻³)	比热容比γ	声速a/(m·s⁻¹)	摩尔质量W/(g·mol⁻¹)
SF₆	6.143	1.094	133.9	146.054
N₂	1.160	1.399	348.9	28.013

下载: 导出CSV

表 2 各区域中压强的理论计算与数值模拟结果对比

Table 2. Comparison of pressure in each region between analytical prediction and numerical simulation

区域	数值模拟结果p_N/Pa	理论计算结果p_A/Pa	相对误差ϒ/%
[0]	101322	101325	−0.003
[0’]	101321	101325	−0.003
[1]	284877	276123	3.073
[2]	348396	353011	−1.325
[3]	348531	353011	−1.285
[4]	208892	199574	4.461
[5]	209139	199574	4.574
[6]	225932	231400	−2.420
[7]	226747	231400	−2.052

下载: 导出CSV

参考文献(34)

[1]	RICHTMYER R D. Taylor instability in shock acceleration of compressible fluids [J]. Communications on Pure and Applied Mathematics, 1960, 13(2): 297–319. DOI: 10.1002/cpa.3160130207.
[2]	MESHKOV E E. Instability of the interface of two gases accelerated by a shock wave [J]. Fluid Dynamics, 1969, 4(5): 101–104. DOI: 10.1007/BF01015969.
[3]	KIFONIDIS K, PLEWA T, SCHECK L, et al. Non-spherical core collapse supernovae: II. the late-time evolution of globally anisotropic neutrino-driven explosions and their implications for SN 1987 A [J]. Astronomy and Astrophysics, 2006, 453(2): 661–678. DOI: 10.1051/0004-6361:20054512.
[4]	SMALYUK V A, WEBER C R, LANDEN O L, et al. Review of hydrodynamic instability experiments in inertially confined fusion implosions on National Ignition Facility [J]. Plasma Physics and Controlled Fusion, 2020, 62(1): 014007. DOI: 10.1088/1361-6587/ab49f4.
[5]	王立锋, 叶文华, 陈竹, 等. 激光聚变内爆流体不稳定性基础问题研究进展 [J]. 强激光与粒子束, 2021, 33(1): 012001. DOI: 10.11884/HPLPB202133.200173. WANG L F, YE W H, CHEN Z, et al. Review of hydrodynamic instabilities in inertial confinement fusion implosions [J]. High Power Laser and Particle Beams, 2021, 33(1): 012001. DOI: 10.11884/HPLPB202133.200173.
[6]	高士清, 邹立勇, 唐久棚, 等. 高马赫数激波作用下单模界面的Richtmyer-Meshkov不稳定性数值模拟 [J]. 爆炸与冲击, 2024, 44(7): 073201. DOI: 10.11883/bzycj-2023-0458. GAO S Q, ZOU L Y, TANG J P, et al. Numerical simulation of single-mode Richtmyer-Meshkov instability caused by high-Mach number shock wave [J]. Explosion and Shock Waves, 2024, 44(7): 073201. DOI: 10.11883/bzycj-2023-0458.
[7]	王涛, 汪兵, 林健宇, 等. 柱形汇聚几何中内爆驱动金属界面不稳定性 [J]. 爆炸与冲击, 2020, 40(5): 052201. DOI: 10.11883/bzycj-2019-0150. WANG T, WANG B, LIN J Y, et al. Numerical investigations of the interface instabilities of metallic material under implosion in cylindrical convergent geometry [J]. Explosion and Shock Waves, 2020, 40(5): 052201. DOI: 10.11883/bzycj-2019-0150.
[8]	ZHOU Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I [J]. Physics Reports, 2017, 720/721/722: 1–136. DOI: 10.1016/j.physrep.2017.07.005.
[9]	邹立勇, 吴强, 李欣竹. 广义Richtmyer-Meshkov不稳定性研究进展 [J]. 中国科学: 物理学力学天文学, 2020, 50(10): 104702. DOI: 10.1360/SSPMA-2020-0024. ZOU L Y, WU Q, LI X Z. Research progress of general Richtmyer-Meshkov instability [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2020, 50(10): 104702. DOI: 10.1360/SSPMA-2020-0024.
[10]	THOMAS V A, KARES R J. Drive asymmetry and the origin of turbulence in an ICF implosion [J]. Physical Review Letters, 2012, 109(7): 075004. DOI: 10.1103/PhysRevLett.109.075004.
[11]	ZHOU Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II [J]. Physics Reports, 2017, 723/724/725: 1-160. DOI: 10.1016/j.physrep.2017.07.008.
[12]	ZHOU Y, SADLER J D, HURRICANE O A. Instabilities and mixing in inertial confinement fusion [J]. Annual Review of Fluid Mechanics, 2025, 57: 197–225. DOI: 10.1146/annurev-fluid-022824-110008.
[13]	ISHIZAKI R, NISHIHARA K, SAKAGAMI H, et al. Instability of a contact surface driven by a nonuniform shock wave [J]. Physical Review E, 1996, 53(6): R5592–R5595. DOI: 10.1103/PhysRevE.53.R5592.
[14]	刘金宏, 邹立勇, 曹仁义, 等. 绕射激波和反射激波作用下N₂/SF₆界面R-M不稳定性实验研究 [J]. 力学学报, 2014, 46(3): 475–479. DOI: 10.6052/0459-1879-13-355. LIU J H, ZOU L Y, CAO R Y, et al. Experimentally study of the Richtmyer-Meshkov instability at N₂/SF₆ flat interfaces by diffracted incident shock waves and reshock [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 475–479. DOI: 10.6052/0459-1879-13-355.
[15]	ZOU L Y, LIU J H, LIAO S F, et al. Richtmyer-Meshkov instability of a flat interface subjected to a rippled shock wave [J]. Physical Review E, 2017, 95(1): 013107. DOI: 10.1103/PhysRevE.95.013107.
[16]	LIAO S F, ZHANG W B, CHEN H, et al. Atwood number effects on the instability of a uniform interface driven by a perturbed shock wave [J]. Physical Review E, 2019, 99(1): 013103. DOI: 10.1103/PhysRevE.99.013103.
[17]	ZOU L Y, AL-MAROUF M, CHENG W, et al. Richtmyer-Meshkov instability of an unperturbed interface subjected to a diffracted convergent shock [J]. Journal of Fluid Mechanics, 2019, 879: 448–467. DOI: 10.1017/jfm.2019.694.
[18]	HE Y F, PENG N F, LI H F, et al. Formation of the cavity on a planar interface subjected to a perturbed shock wave [J]. Physical Review Fluids, 2023, 8(6): 063402. DOI: 10.1103/PhysRevFluids.8.063402.
[19]	ZHANG E L, LIAO S F, ZOU L Y, et al. Refraction of a triple-shock configuration at planar fast-slow gas interfaces [J]. Journal of Fluid Mechanics, 2024, 984: A49. DOI: 10.1017/jfm.2024.245.
[20]	ZHANG W B, WU Q, ZOU L Y, et al. Mach number effect on the instability of a planar interface subjected to a rippled shock [J]. Physical Review E, 2018, 98(4): 043105. DOI: 10.1103/PhysRevE.98.043105.
[21]	王震, 王涛, 柏劲松, 等. 流场非均匀性对非平面激波诱导的Richtmyer-Meshkov不稳定性影响的数值研究 [J]. 爆炸与冲击, 2019, 39(4): 041407. DOI: 10.11883/bzycj-2018-0342. WANG Z, WANG T, BAI J S, et al. Numerical study of non-uniformity effect on Richtmyer-Meshkov instability induced by non-planar shock wave [J]. Explosion And Shock Waves, 2019, 39(4): 041407. DOI: 10.11883/bzycj-2018-0342.
[22]	ZHANG Y M, ZHAO Y, DING J C, et al. Richtmyer-Meshkov instability with a rippled reshock [J]. Journal of Fluid Mechanics, 2023, 968: A3. DOI: 10.1017/jfm.2023.491.
[23]	张崇玉, 胡海波, 王翔, 等. 铅飞层中斜冲击波对碰马赫反射行为实验研究 [J]. 爆炸与冲击, 2019, 39(4): 043102. DOI: 10.11883/bzycj-2017-0441. ZHANG C Y, HU H B, WANG X, et al. Experimental study of Mach reflection induced by collision of oblique shock waves in a lead plate [J]. Explosion and Shock Waves, 2019, 39(4): 043102. DOI: 10.11883/bzycj-2017-0441.
[24]	张崇玉, 胡海波, 王翔. 平面金属飞层对碰区速度剖面的精密测试 [J]. 爆炸与冲击, 2016, 36(4): 557–561. DOI: 10.11883/1001-1455(2016)04-0557-05. ZHANG C Y, HU H B, WANG X. Precision test of velocity profile in collision region of plane metal flying layer [J]. Explosion and Shock Waves, 2016, 36(4): 557–561. DOI: 10.11883/1001-1455(2016)04-0557-05.
[25]	陈大伟, 秦承森, 王裴, 等. 凝聚介质中斜激波的反射 [J]. 计算物理, 2011, 28(6): 791–796. DOI: 10.3969/j.issn.1001-246X.2011.06.001. CHEN D W, QIN C S, WANG P, et al. Oblique shock wave reflection in condensed matter [J]. Chinese Journal of Computational Physics, 2011, 28(6): 791–796. DOI: 10.3969/j.issn.1001-246X.2011.06.001.
[26]	WOODWARD P, COLELLA P. The numerical simulation of two-dimensional fluid flow with strong shocks [J]. Journal of Computational Physics, 1984, 54(1): 115–173. DOI: 10.1016/0021-9991(84)90142-6.
[27]	ZHENG H W, SHU C, CHEW Y T, et al. A solution adaptive simulation of compressible multi-fluid flows with general equation of state [J]. International Journal for Numerical Methods in Fluids, 2011, 67(5): 616–637. DOI: 10.1002/fld.2380.
[28]	LI L F, JIN T, ZOU L Y, et al. Numerical study of Richtmyer–Meshkov instability of a flat interface driven by perturbed and reflected shock waves [J]. Physics of Fluids, 2023, 35(2): 026104. DOI: 10.1063/5.0137389.
[29]	SUTHERLAND W. LII. The viscosity of gases and molecular force [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1893, 36(223): 507–531. DOI: 10.1080/14786449308620508.
[30]	BEN-DOR G. Shock wave reflection phenomena [M]. 2nd ed. Heidelberg: Springer, 2007. DOI: 10.1007/978-3-540-71382-1.
[31]	HENDERSON L F, LOZZI A. Experiments on transition of Mach reflexion [J]. Journal of Fluid Mechanics, 1975, 68(1): 139–155. DOI: 10.1017/S0022112075000730.
[32]	王继海. 爆轰波在物质介面上的折射 [J]. 爆炸与冲击, 1981, 1(2): 1–11. DOI: 10.11883/1001-1455(1981)02-0001-11. WANG J H. Refraction of detonation waves on material interface [J]. Explosion and Shock Waves, 1981, 1(2): 1–11. DOI: 10.11883/1001-1455(1981)02-0001-11.
[33]	ANDERSON JR J D. Fundamentals of aerodynamics [M]. 6th ed. New York: McGraw Hill, 2016: 978-1259129919.
[34]	SAMTANEY R, ZABUSKY N J. Circulation deposition on shock-accelerated planar and curved density-stratified interfaces: models and scaling laws [J]. Journal of Fluid Mechanics, 1994, 269: 45–78. DOI: 10.1017/S0022112094001485.